Institut für Softwaretechnologie Risky Business Model-based Statistical Testing

Institut für Softwaretechnologie Risky Business Model-based Statistical Testing Mathias Winder AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 1/6

Institut für Softwaretechnologie Content Ø An Usage Model based on UML-Statemachines Ø Risk-based Modeling Ø The Idea of Risk-based Testing Ø Risk- and Model-based Testing Ø Graph-oriented Testcase Generation Ø UML-Statemachines and Graphs Ø Markov Chain Usage Models Ø Generating Transition Probabilities Ø Risk-based Priorization AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 2/6

Institut für Softwaretechnologie An Usage Model based on UMLStatemachines Ø UML-Statemachines are very powerful Difficult to automate Reduce number of different elements Ø Subset with enough elements to define (semantically correct) Usage Models: Ø States: Ø Do. Activity define activities processed while state is active Ø Composite States and Submachine States contain (or refer) other Regions Ø Final States defines the end of the usage Ø Pseudostates: initial, junction, choice Ø Transitions: Ø Trigger: an event (e. g. Mouse Click) firing the transition Ø Guard: a condition, that the transition can be fired Ø Effect: a behavior caused by the transition AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 3/6

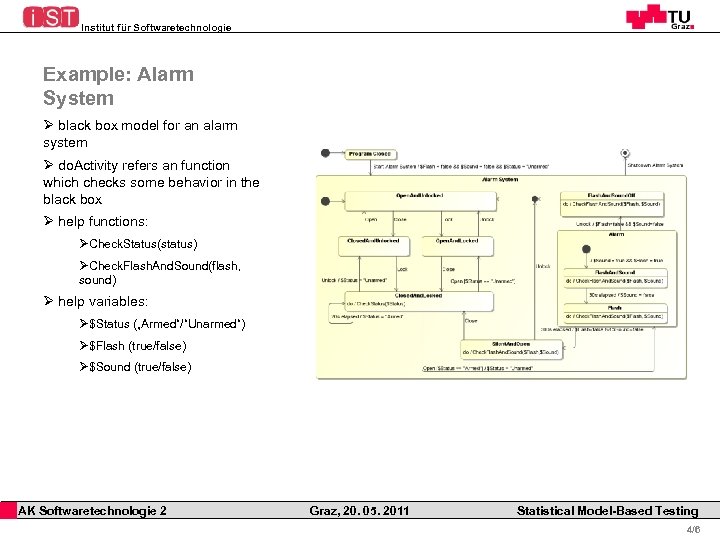
Institut für Softwaretechnologie Example: Alarm System Ø black box model for an alarm system Ø do. Activity refers an function which checks some behavior in the black box Ø help functions: ØCheck. Status(status) ØCheck. Flash. And. Sound(flash, sound) Ø help variables: Ø$Status („Armed“/“Unarmed“) Ø$Flash (true/false) Ø$Sound (true/false) AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 4/6

Institut für Softwaretechnologie Content Ø An Usage Model based on UML-Statemachines Ø Risk-based Modeling Ø The Idea of Risk-based Testing Ø Risk- and Model-based Testing Ø Graph-oriented Testcase Generation Ø UML-Statemachines and Graphs Ø Markov Chain Usage Models Ø Generating Transition Probabilities Ø Risk-based Priorization AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 5/6

Institut für Softwaretechnologie The Idea of Risk-based Testing Ø Large Scaled Systems are very complex and normally there aren`t enough resources to test every feature of the System in detail Ø Some features are more important than others: Ø more complex implementation probability of failure Ø damage, if the feature fails: Ø for costumer (use of the software, costs, . . . ) Ø for company (maintainance, . . . ) Ø Idea: Use metrics to estimate the Risk of the features and focus on more risky areas while testing Ø e. g. , risk = (probability of failure) * damage AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 6/6

Institut für Softwaretechnologie Risk- and Model-based Testing Ø Annotated Risks on Usage Models can be used to achieve Testcases focused on risky areas Ø Goal: Ø Find the most interesting Paths/Testcases Ø A Risk raises the interest, but a Risk get`s less interesting if it`s repeated more often (How to estimate interest? ) Ø Standard Workflow: Ø Create Usage Model and assess Risks for important features (for single transitions or whole regions) Ø Generate Testcases (e. g. using Random Walk) Ø Estimate and priorize Testcases based on Risks AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 7/6

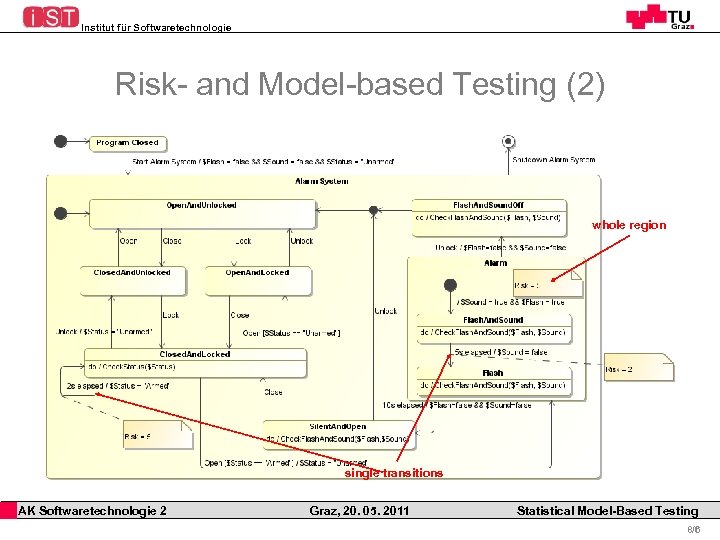
Institut für Softwaretechnologie Risk- and Model-based Testing (2) whole region single transitions AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 8/6

Institut für Softwaretechnologie Content Ø An Usage Model based on UML-Statemachines Ø Risk-based Modeling Ø The Idea of Risk-based Testing Ø Risk- and Model-based Testing Ø Graph-oriented Testcase Generation Ø UML-Statemachines and Graphs Ø Markov Chain Usage Models Ø Generating Transition Probabilities Ø Risk-based Priorization AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 9/6

Institut für Softwaretechnologie Graph-oriented Testcase Generation Ø Idea: Use well-known graph-algorithms to derive Testcases from Usage Models: Ø coverage-based algorithms (e. g. Chinese Postman) Ø search-based algorithms (e. g. A*) Ø random-based algorithms (e. g. Random. Walk) Ø But: Ø Usage Model have to be interpreted as Graph Ø Usage Model are normally not static (there are conditions like Guards/Precondition/. . . ) Adaption of algorithms AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 10/6

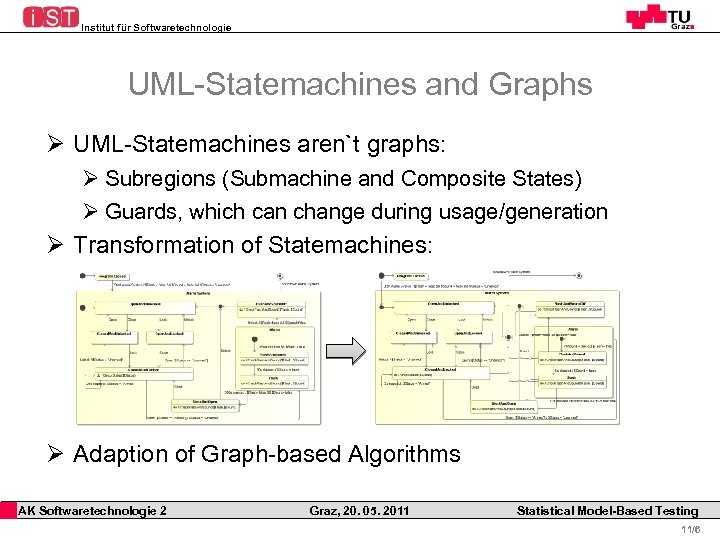
Institut für Softwaretechnologie UML-Statemachines and Graphs Ø UML-Statemachines aren`t graphs: Ø Subregions (Submachine and Composite States) Ø Guards, which can change during usage/generation Ø Transformation of Statemachines: Ø Adaption of Graph-based Algorithms AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 11/6

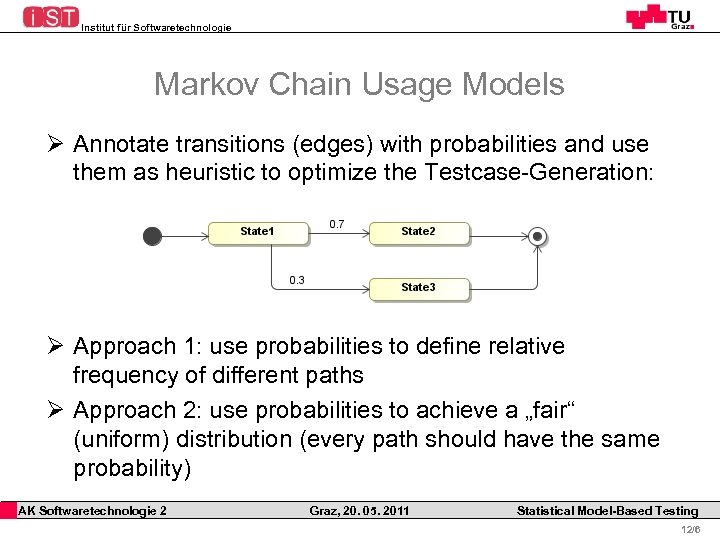
Institut für Softwaretechnologie Markov Chain Usage Models Ø Annotate transitions (edges) with probabilities and use them as heuristic to optimize the Testcase-Generation: Ø Approach 1: use probabilities to define relative frequency of different paths Ø Approach 2: use probabilities to achieve a „fair“ (uniform) distribution (every path should have the same probability) AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 12/6

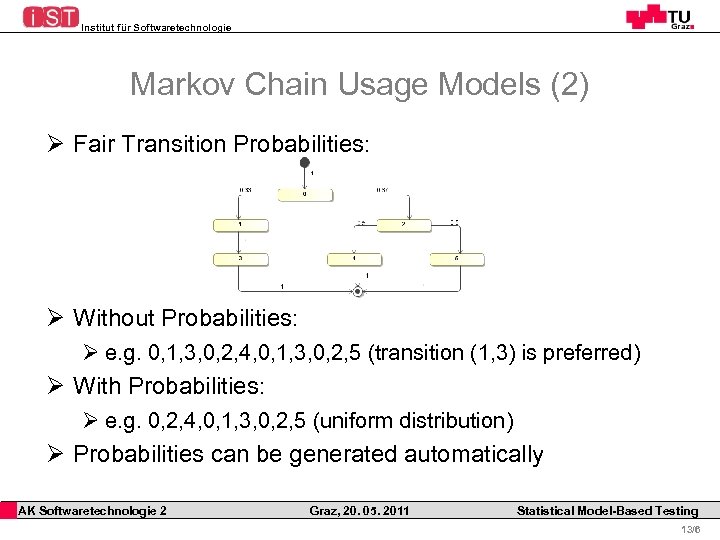
Institut für Softwaretechnologie Markov Chain Usage Models (2) Ø Fair Transition Probabilities: Ø Without Probabilities: Ø e. g. 0, 1, 3, 0, 2, 4, 0, 1, 3, 0, 2, 5 (transition (1, 3) is preferred) Ø With Probabilities: Ø e. g. 0, 2, 4, 0, 1, 3, 0, 2, 5 (uniform distribution) Ø Probabilities can be generated automatically AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 13/6

Institut für Softwaretechnologie Generating Transition Probabilities Ø Basic Approach: Ø Generate a path using the Chinese Postman Problem (with a fictitious transition between final and intial state) Ø Count the use of every Node n: N[n] = #n in path Ø Count the use of every Transition t: T[t] = #t in path Ø Probability of Transition t: P[t] = T[t] / N[t. Source] Ø E. g. (example from previous slide): Ø Path: initial, 0, 2, 4, final, initial, 0, 1, 3, final, initial, 0, 2, 5 Ø Probability for transition t(0, 2): P[t(0, 2)] = T[t(0, 2)] / N[0] = 2/3 = 0. 67 Ø Problem: Chinese Postman is NP-Complete We need good approximations AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 14/6

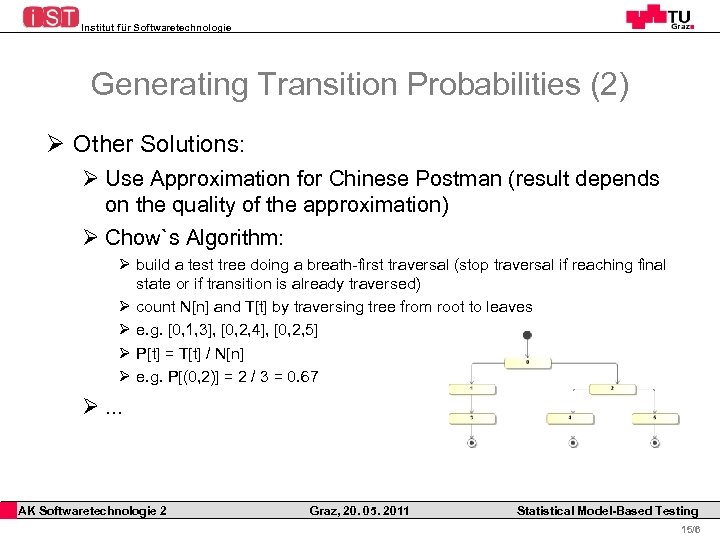
Institut für Softwaretechnologie Generating Transition Probabilities (2) Ø Other Solutions: Ø Use Approximation for Chinese Postman (result depends on the quality of the approximation) Ø Chow`s Algorithm: Ø build a test tree doing a breath-first traversal (stop traversal if reaching final state or if transition is already traversed) Ø count N[n] and T[t] by traversing tree from root to leaves Ø e. g. [0, 1, 3], [0, 2, 4], [0, 2, 5] Ø P[t] = T[t] / N[n] Ø e. g. P[(0, 2)] = 2 / 3 = 0. 67 Ø. . . AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 15/6

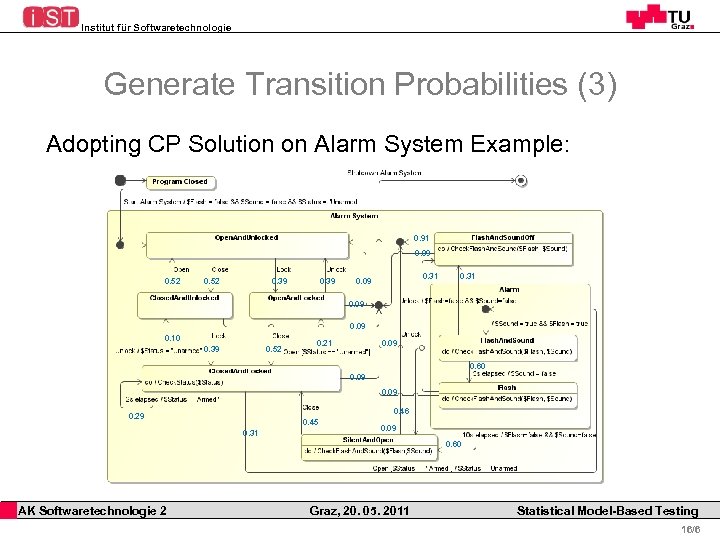
Institut für Softwaretechnologie Generate Transition Probabilities (3) Adopting CP Solution on Alarm System Example: 0. 91 0. 09 0. 52 0. 39 0. 31 0. 09 0. 10 0. 39 0. 52 0. 21 0. 09 0. 60 0. 09 0. 46 0. 29 0. 45 0. 31 0. 09 0. 60 AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 16/6

Institut für Softwaretechnologie Content Ø An Usage Model based on UML-Statemachines Ø Risk-based Modeling Ø The Idea of Risk-based Testing Ø Risk- and Model-based Testing Ø Graph-oriented Testcase Generation Ø UML-Statemachines and Graphs Ø Markov Chain Usage Models Ø Generating Transition Probabilities Ø Risk-based Priorization AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 17/6

Institut für Softwaretechnologie Risk-based Priorization Ø Assume we have a (big) list of generated testcases: Ø Which testcase should be executed first? (depending to ressources we maybe cannot execute all) Ø Priorize testcases in the list to decide which testcases are executed first Ø Static Risk-based Priorization: Ø For each Testcase tc: Calculate the Risk Exposure RE which is the sum of Risks achieved by the Testcase (RE[tc] = Sum(R in tc)) Ø Order the Testcases by RE AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 18/6

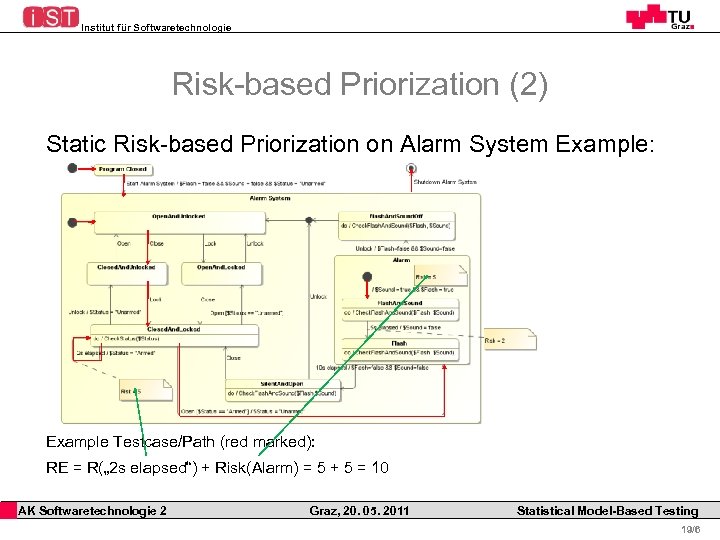
Institut für Softwaretechnologie Risk-based Priorization (2) Static Risk-based Priorization on Alarm System Example: Example Testcase/Path (red marked): RE = R(„ 2 s elapsed“) + Risk(Alarm) = 5 + 5 = 10 AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 19/6

Institut für Softwaretechnologie Risk-based Priorization (3) Ø Dynamic Risk-based Priorization: Ø Given: list of testcases L Ø Create Empty List P Ø Use a Heuristic, which assess the interest of testing a feature depending on risk and the count, how often the Risk was used in prior testcases: e. g. Interest(R) = R * 0. 5^Prior. Usings. Of. R Ø While list of testcases is not empty: Ø Find testcase TC in L with the hightest interest (Sum of Interest) Ø Remove TC from L and add TC to P Ø P is the Priorized List AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 20/6

Institut für Softwaretechnologie Short Case Study Ø Alarm System with mutant in risky area: Ø mutant: sound does not turn off automatically Ø Chinese Postman for Transition Probabilities Ø Testcases generated by Random Walk (using Probabilities as Heuristic) and priorized with dynamic Priorization (Interest(R) = R * 0. 5^Prior. Usings. Of. R) Ø Mutant found by priorized testcases 1, 2 and 9 (Total: 15) AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 21/6

Institut für Softwaretechnologie References [1] A. Feliachi and H. Le Guen, „Generating transition probabilities for automatic model-based test generation“ (2010) [2] H. Stallbaum, A. Metzger and K. Pohl, “An Automated Technique for Risk-based Test Case Generation and Prioritization” (2008) [3] Y. Chen and R. Probert, „A Risk-based Regression Test Selection Strategy” (2003) [4] S. Amland, „Risk Based Testing and Metrics: Risk analysis fundamentals and metrics for software testing including a financial application” (2000) [5] J. Whittaker and M. Thomason, „A Markov chain model for statistical software testing” (1994) AK Softwaretechnologie 2 Graz, 20. 05. 2011 Statistical Model-Based Testing 22/6