- Количество слайдов: 63

Instance Based Learning Soongsil University Intelligent Systems Lab. 1

Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR) 2

Instance-based learning n n n One way of solving tasks of approximating discrete or real valued target functions Have training examples: (xn, f(xn)), n=1. . N. Key idea: n n just store the training examples when a test example is given then find the closest matches 3

Motivation: Eager Learning n n The Learning Task: Try to approximate a target function through a hypothesis on the basis of training examples EAGER Learning: As soon as the training examples and the hypothesis space are received the search for the first hypothesis begins n n n Training phase: given: training examples D=<Xi, f(Xi)> hypothesis space H search: best hypothesis Processing phase: for every new instance xq return Examples 4

Motivation: Lazy Algorithms n LAZY ALGORITHMS: n Training examples are stored and sleeping n Generalisation beyond these examples is postponed till new instances must be classified n Every time a new query instance is encountered, its relationship to the previously stored examples is examined in order to compute the value of the target function for this new instance 5

Motivation: Instance-Based Learning n Instance-Based Algorithms can establish a new local approximation for every new instance n Training phase: given: training sample D=<Xi, f(Xi)> n Processing phase: given: instance xq search: best local hypothesis return n Examples: n n Nearest Neighbour Algorithm Distance Weighted Nearest Neighbour Locally Weighted Regression. . 6

Motivation: Instance-Based Learning n n n How are the instances represented? How can we measure the similarity of the instances? How can be computed? 7

Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR)
X X

Nearest Neighbour Algorithm n n Idea: All instances correspond to the points in the n-dimensional space. Assign the value of the next, neighboured instance to the new instance Representation: Let be an instance, where denotes the value of the r-th attribute of an instance x We may also use Xir instead of n Target Function: Discrete valued or real valued

1 -Nearest Neighbor Four things make a memory based learner: 1. A distance metric Euclidian 2. How many nearby neighbors to look at? One 3. A weighting function (optional) Unused 4. How to fit with the local points? Just predict the same output as the nearest neighbor. 11

Nearest Neighbour Algorithm n HOW IS FORMED? n Discrete target function: where V: set of s classes (e. g. , red, black, yellow…) n Continuous target function: n Let the next neighbour of

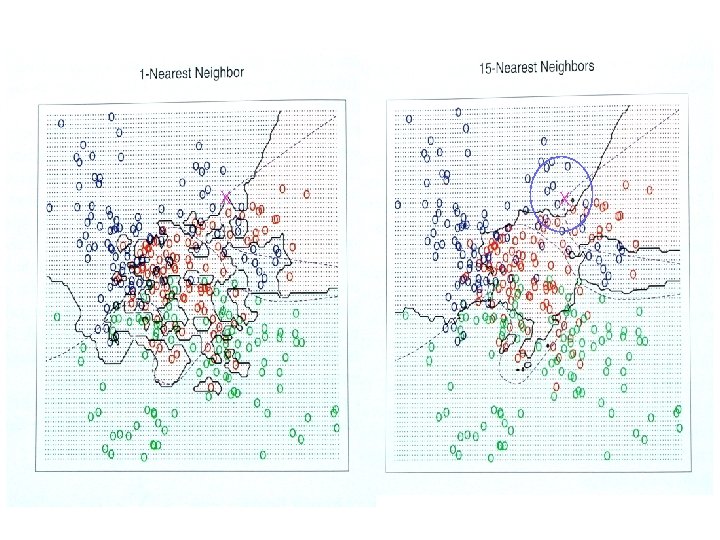
Nearest Neighbour Algorithm n 1 -Nearest neighbour: Given a query instance xq, • first locate the nearest training example xn • then f(xq): = f(xn) n K-Nearest neighbour: Given a query instance xq, • first locate the k nearest training examples • If discrete values target function, take vote among its k nearest neighbour. (e. g. , X, X, O, O, X, X) X Else if real valued target faction, take the mean of the f values of the k nearest neighbour 13

How to choose “k” n Average of k points more reliable when: n n Large k: n n n less sensitive to noise (particularly class noise) better probability estimates for discrete classes larger training sets allow larger values of k Small k: n n noise in attributes noise in class labels classes partially overlap captures fine structure of problem space better may be necessary with small training sets Balance must be struck between large and small k As training set approaches infinity, and k grows large, k. NN becomes Bayes optimal if p (x) >. 5 then predict 1, else 0 14

k-Nearest Neighbor Four things make a memory based learner: 1. A distance metric Euclidian 2. How many nearby neighbors to look at? k 3. A weighting function (optional) Unused 4. How to fit with the local points? Just predict the average output among the k nearest neighbors. 15

k-Nearest Neighbour n n n Idea: If we choose k=1, then the algorithm assigns to where is the nearest training instance to the value For larger values of k the algorithm assigns the most common value among the k nearest training examples How can where be established ? if , otherwise Let xi, …xk denote the k instances from training examples that are nearest to xq

The distance between examples n n n We need a measure of distance in order to know who are the neighbours Assume that we have T attributes for the learning problem. Then one example point x has elements xt , t=1, …T. The distance between two points xi , xj is often defined as the Euclidean distance: 17

Similarity and Dissimilarity Between Objects n n n Distances are normally used measures Minkowski distance: a generalization If q = 2, d is Euclidean distance If q = 1, d is Manhattan distance Weighed distance

k-Nearest Neighbour n REFINEMENT: The weights of the neighbours are taken into account relative to their distance to the query point. The farther a neighbour the less is its influence. . . where if , otherwise To accommodate the case where the query point exactly matches one of the training instances and the denominator therefore is zero, we assign to be in this case n Distance-weight for real-valued target function:

Voronoi Diagram n Example: 1 NN: n 5 -NN: Voronoi Diagram: The decision surface is induced by a 1 -Nearest Neighbour algorithm for a typical set of training examples. The convex surrounding of each training example indicates the region of query points whose classification will be completely determined by the training example. 20

Characteristics of Inst-b-Learning n n An instance-based learner is a lazy-learner and does all the work when the test example is presented. This is opposed to so-called eager-learners, which build a parameterised compact model of the target. It produces local approximation to the target function (different with each test instance) 21

When to consider Nearest Neighbour algorithms? n n Instances map to points in Not more than say 20 attributes per instance Lots of training data Advantages: n n Training is very fast Can learn complex target functions Don’t lose information Disadvantages: n ? (will see them shortly…) 22
one two three four five six seven Eight ? 23
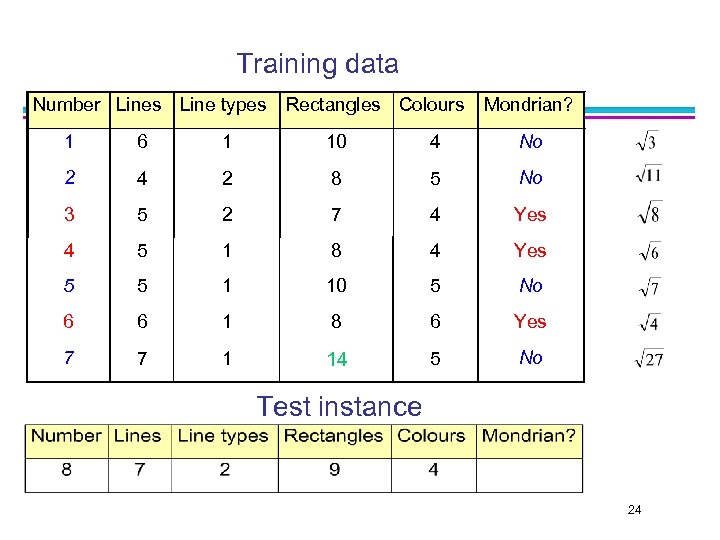
Training data Number Lines Line types Rectangles Colours Mondrian? 1 6 1 10 4 No 2 4 2 8 5 No 3 5 2 7 4 Yes 4 5 1 8 4 Yes 5 5 1 10 5 No 6 6 1 8 6 Yes 7 7 1 14 5 No Test instance 24

Keep data in normalised form One way to normalise the data ar(x) to a´r(x) is 25
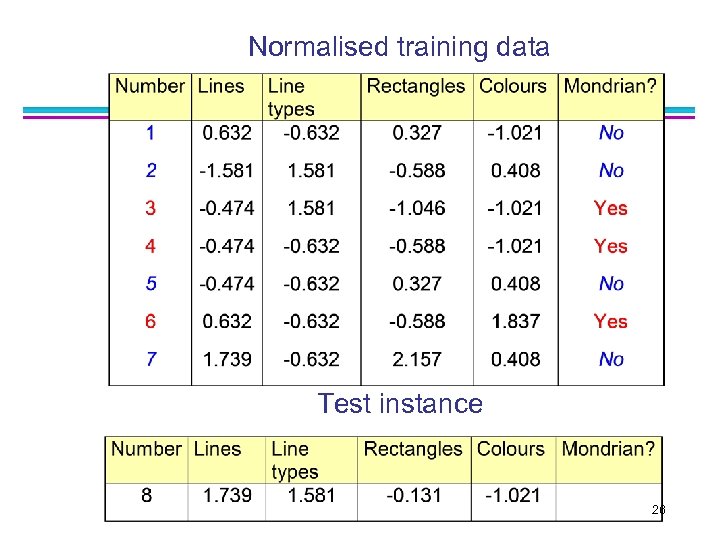
Normalised training data Test instance 26
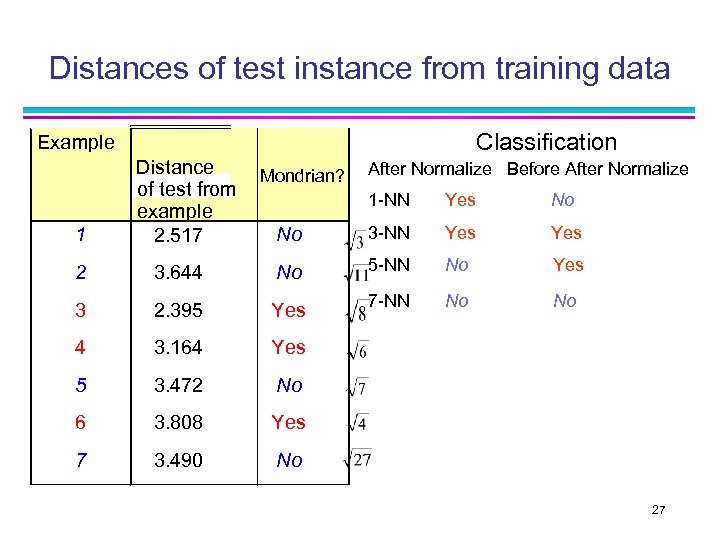
Distances of test instance from training data Classification Example 1 Distance Mondrian? of test from example No 2. 517 After Normalize Before After Normalize 1 -NN Yes No 3 -NN Yes 2 3. 644 No 5 -NN No Yes 3 2. 395 Yes 7 -NN No No 4 3. 164 Yes 5 3. 472 No 6 3. 808 Yes 7 3. 490 No 27

Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR)

What if the target function is real valued? n The k-nearest neighbour algorithm would just calculate the mean of the k nearest neighbours 29

Distance-Weighted KNN w Might want nearer neighbors with more heavy weight: w For discrete-valued target functions: w For real-valued target functions: n Shepard method 30

Remarks on k-Nearest Neighbour Algorithm n PROBLEM: The measurement of the distance between two instances considers every attribute. So even irrelevant attributes can influence the approximation. n EXAMPLE: n =20 but only 2 attributes are relevant n SOLUTION: Weight each attribute differently when calculating the distance between two neighbours: n stretching the relevant axes in Euclidian space: shortening the axes that correspond to less relevant attributes n lengthening the axes that correspond to more relevant attribute n PROBLEM: Determine which weight belongs to which attribute automatically? n Cross-validation n Leave-one-out see in next lecture

Remarks on k-Nearest Neighbour Algorithm 2 n ADVANTAGE: n The training phase is processed very fast n Can learn complex target function n Robust to noisy training data n Quite effective when a sufficiently large set of training data is provided n DISADVANTAGE: n Alg. delays all processing until a new query is received => significant computation can be required to process; efficient memory indexing n Processing is slow n Sensibility about escape of the dimensions n BIAS: Inductive bias corresponds to an assumption that the classification of an instance will be most similar to the classification of other instances that are nearby in Euclidean distance

Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR)

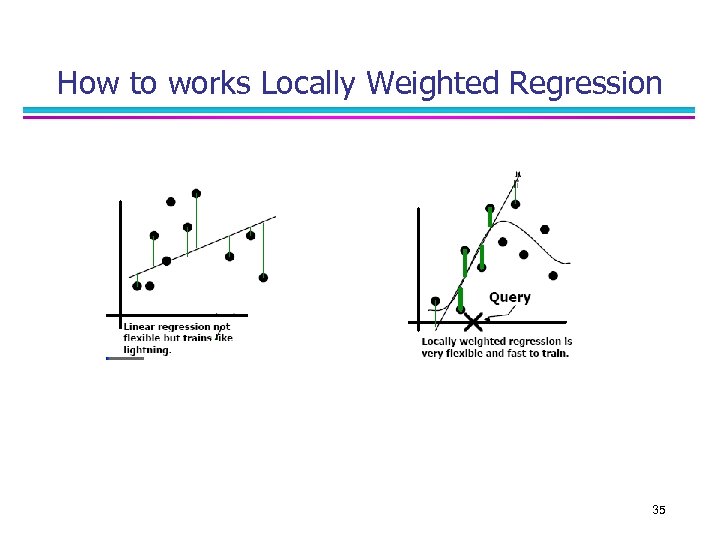
Locally Weighted Regression n IDEA: Generalization of Nearest Neighbour Alg. It constructs an explicit approximation to f over a local region surrounding xq. It uses nearby or distance-weighted training examples to form the local approximation to f. n Local: The function is approximated based solely on the training data near the query point n Weighted: The construction of each training example is weighted by its distance from the query point n Regression: means approximating a real-valued target function
How to works Locally Weighted Regression 35

Locally Weighted Regression n PROCEDURE: n Given a new query xq , construct an approximation that fits the training examples in the neighbourhood surrounding xq n This approximation is used to calculate , which is as the estimated target value assigned to the query instance. n The description of may change, because a different local approximation will be calculated for each instance

Locally Weighted Linear Regression n Special case of LWR, simple computation n LINEAR HYPOTHESIS SPACE: where ar(x) is the rth attribute of x, x variable of the hypotheses space n Define the error criterion E in order to emphasize the fitting of the local training example n Minimise the squared error over just k nearest neighbours: n Minimise the squared error over the entire set D using some kernel function K to decrease this error based on the distance n Combine E 1 and E 2

Locally Weighted Linear Regression w Using linear function to approximate f: w Recall chapter 4: n gradient descent rule

Locally Weighted Linear Regression 2 n The third error criterion is a good approximation to the second one and it has the advantage that computational costs are independent of the total number of training examples n If E 3 is chosen and the gradient descent rule is rederived (see NN) the following training rule is obtained

Evaluation Locally Weighted Regression n ADVANTAGE n Pointwise approximation of a complex target function n Earlier data has no influence on the new ones n DISADVANTAGE n The quality of the result depends on n Choice of the function n Choice of the kernel function K n Choice of the hypothesis space H n Sensibility against the relevant and irrelevant attributes

Difficulties with k-nearest neighbour algorithms n n Have to calculate the distance of the test case from all training cases There may be irrelevant attributes amongst the attributes – curse of dimensionality 41

Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR)

Radial Basis Function (RBF) Networks n n Each prototype node computes a distance based kernel function (Gaussian is common) Prototype nodes form a hidden layer in a neural network Train top layer with simple delta rule to get outputs Thus, prototype nodes learn weightings for each class blend of instance-based method and neural network method. 43

Radial Basis Function w Function to be learned: One common choice for is: w Global approximation to target function, in terms of linear combination of local approximations. w Related to distance-weighted regression, “eager” instead of “lazy”. 44

Training RBF Networks w Stage one: define hidden units by choosing k, xu and n Allocate Gaussian kernel function for each training example <x i, f(xi)>. n Choose set of kernel functions that is smaller than the number of training examples. w Scatter uniformly over instance space w Or nonuniformly w Stage two: train wu n Gradient descent by global error criterion 45
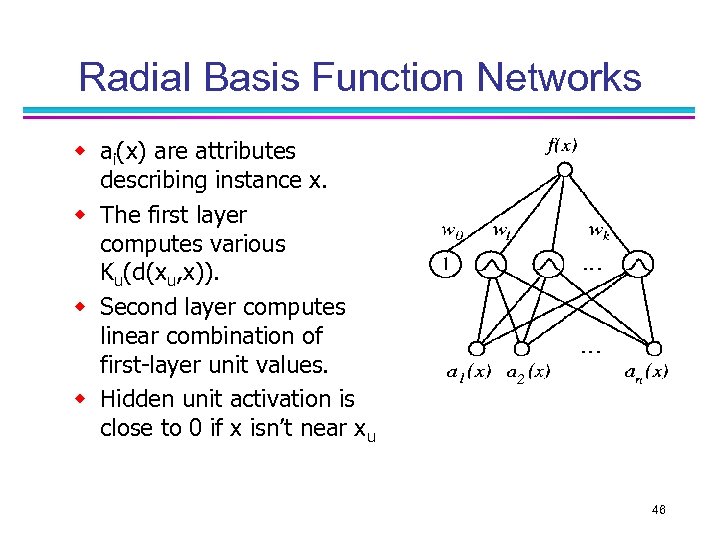
Radial Basis Function Networks w ai(x) are attributes describing instance x. w The first layer computes various Ku(d(xu, x)). w Second layer computes linear combination of first-layer unit values. w Hidden unit activation is close to 0 if x isn’t near xu 46


Content n Motivation n n n n Eager Learning Lazy Learning Instance-Based Learning k-Nearest Neighbour Learning Distance-Weighted k-NN Locally Weighted Regression Radial Basis Functions Case-Based Reasoning Summary (k. NN) (LWR) (RBF) (CBR)

Case-based reasoning (CBR) n Instance-based methods and locally weighted regression: n n n lazy learning; They classify new query instances by analysing similar instances and ignoring the very different ones They represent instances as real-valued points in an n-dimensional Euclidian space CBR: first two principles and instances are represented by using a richer symbolic description and the methods used to retrieval CBR is an advanced instance based learning applied to more complex instance objects Objects may include complex structural descriptions of cases & adaptation rules

n n n CBR cannot use Euclidean distance measures Must define distance measures for those complex objects instead (e. g. semantic nets) CBR tries to model human problem-solving n n n uses past experience (cases) to solve new problems retains solutions to new problems CBR is an ongoing area of machine learning research with many applications

Applications of CBR n Design n n Planning n n repair schedules Diagnosis n n landscape, building, mechanical, conceptual design of aircraft sub-systems medical Adversarial reasoning n legal 51
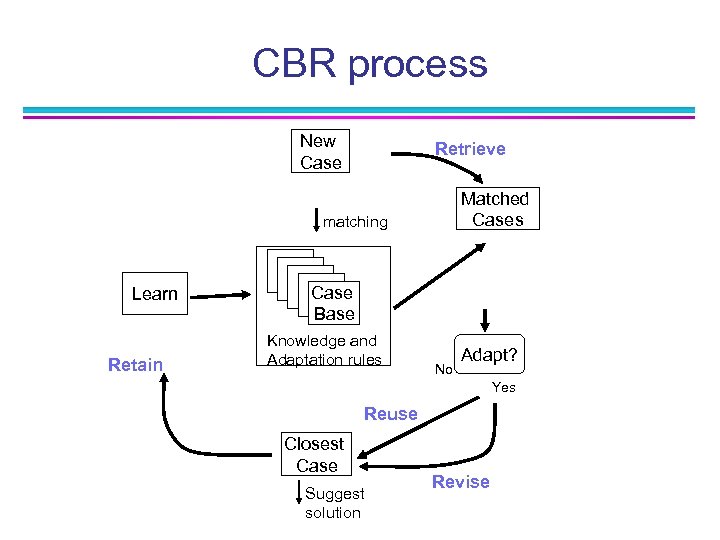
CBR process New Case Retrieve Matched Cases matching Learn Retain Case Base Knowledge and Adaptation rules No Adapt? Yes Reuse Closest Case Suggest solution Revise
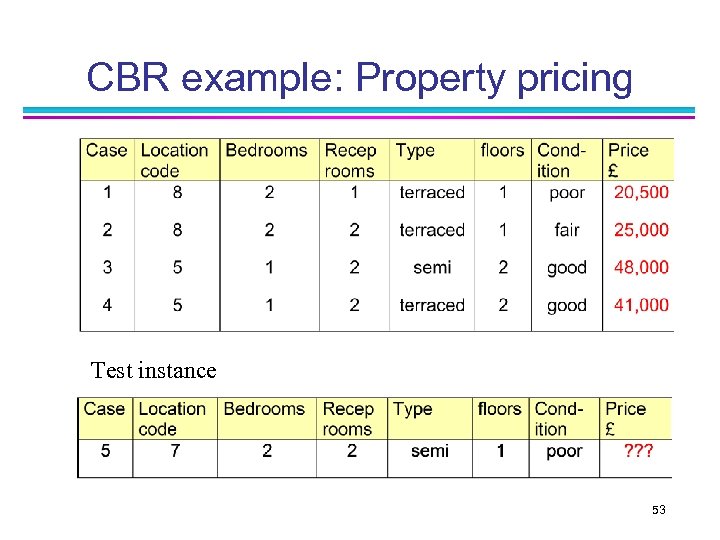
CBR example: Property pricing Test instance 53

How rules are generated n n There is no unique way of doing it. Here is one possibility: Examine cases and look for ones that are almost identical n case 1 and case 2 n n R 1: If recep-rooms changes from 2 to 1 then reduce price by £ 5, 000 case 3 and case 4 n R 2: If Type changes from semi to terraced then reduce price by £ 7, 000 54

Matching n Comparing test instance n n n matches(5, 1) = 3 matches(5, 2) = 3 matches(5, 3) = 2 matches(5, 4) = 1 Estimate price of case 5 is £ 25, 000 55

Adapting n Reverse rule 2 n n if type changes from terraced to semi then increase price by £ 7, 000 Apply reversed rule 2 n new estimate of price of property 5 is £ 32, 000 56

Learning n So far we have a new case and an estimated price n n nothing is added yet to the case base If later we find house sold for £ 35, 000 then the case would be added n could add a new rule n if location changes from 8 to 7 increase price by £ 3, 000 57

Problems with CBR n n How should cases be represented? How should cases be indexed for fast retrieval? How can good adaptation heuristics be developed? When should old cases be removed? 58

Advantages n n n A local approximation is found for each test case Knowledge is in a form understandable to human beings Fast to train 59

Lazy and Eager Learning w Lazy: wait for query before generalizing n KNN, locally weighted regression, CBR w Eager: generalize before seeing query n RBF networks w Differences: n Computation time n Global and local approximations to the target function n Use same H, lazy can represent more complex functions. (e. g. , consider H=linear functions) 60

Summary w Differences and advantages w KNN algorithm: the most basic instance-based method. w Locally weighted regression: generalization of KNN. w RBF networks: blend of instance-based method and neural network method. w Case-based reasoning 61

Lazy and Eager Learning n Lazy: wait for query before generalizing n n Eager: generalize before seeing query n n k-Nearest Neighbour, Case based reasoning RBF Networks, ID 3, … Does it matter? n n Eager learner must create global approximation Lazy learner can create many local approximations 62

The End