aba63d6bcdead89b842ada0f5b5c24d8.ppt
- Количество слайдов: 29

Instance Based Learning Ata Kaban The University of Birmingham 1

Today we learn: n K-Nearest Neighbours n Case-based reasoning n Lazy and eager learning 2

Instance-based learning n n n One way of solving tasks of approximating discrete or real valued target functions Have training examples: (xn, f(xn)), n=1. . N. Key idea: – just store the training examples – when a test example is given then find the closest matches 3

n 1 -Nearest neighbour: Given a query instance xq, • first locate the nearest training example xn • then f(xq): = f(xn) n K-Nearest neighbour: Given a query instance xq, • first locate the k nearest training examples • if discrete values target function then take vote among its k nearest nbrs else if real valued target fct then take the mean of the f values of the k nearest nbrs 4

The distance between examples n n n We need a measure of distance in order to know who are the neighbours Assume that we have T attributes for the learning problem. Then one example point x has elements xt , t=1, …T. The distance between two points xi xj is often defined as the Euclidean distance: 5
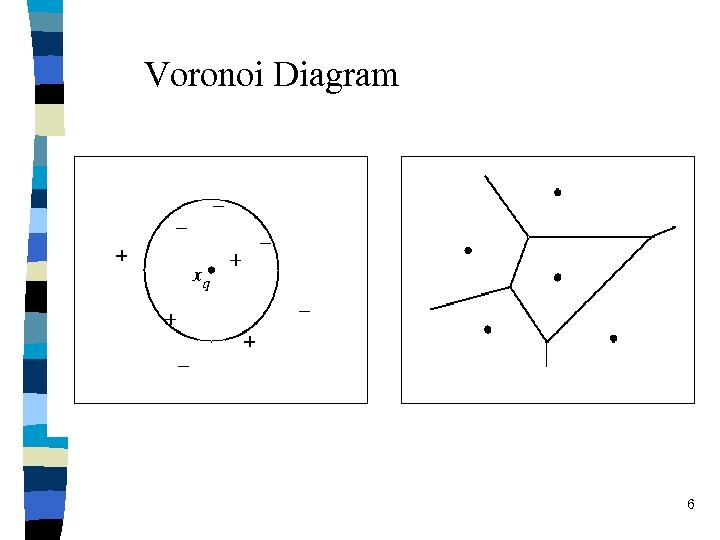
Voronoi Diagram 6

Characteristics of Inst-b-Learning n n An instance-based learner is a lazy-learner and does all the work when the test example is presented. This is opposed to so-called eager-learners, which build a parameterised compact model of the target. It produces local approximation to the target function (different with each test instance) 7

When to consider Nearest Neighbour algorithms? n n Instances map to points in Not more then say 20 attributes per instance Lots of training data Advantages: – Training is very fast – Can learn complex target functions – Don’t lose information n Disadvantages: – ? (will see them shortly…) 8
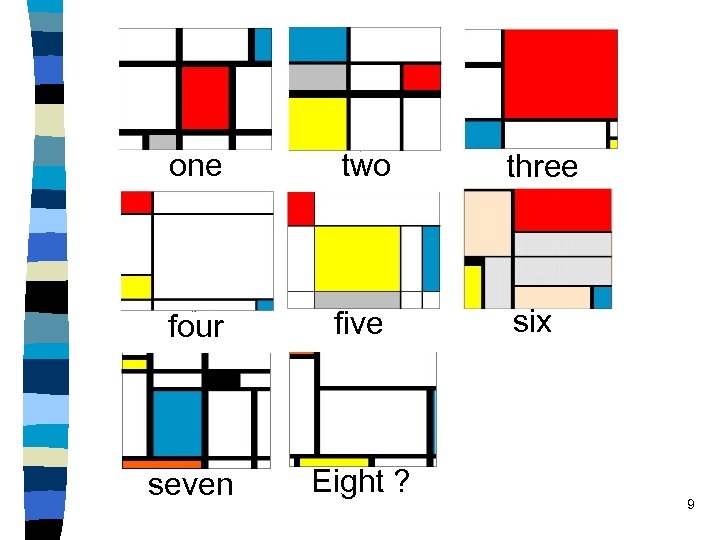
one two three four five six seven Eight ? 9
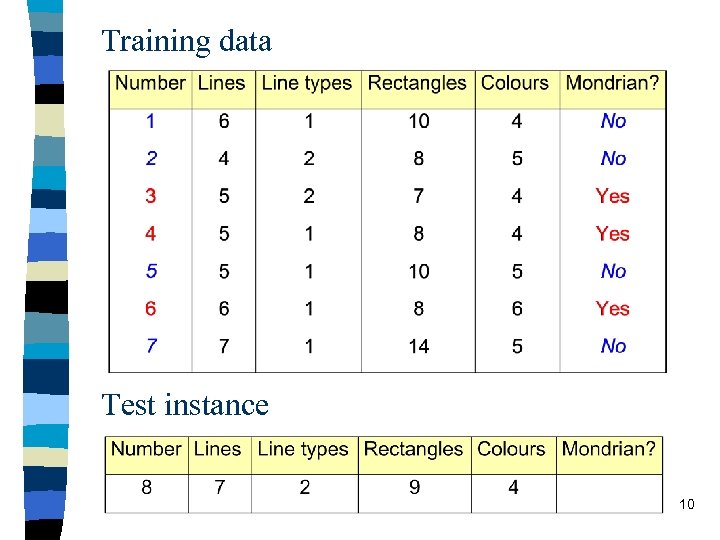
Training data Test instance 10

Keep data in normalised form One way to normalise the data ar(x) to a´r(x) is 11
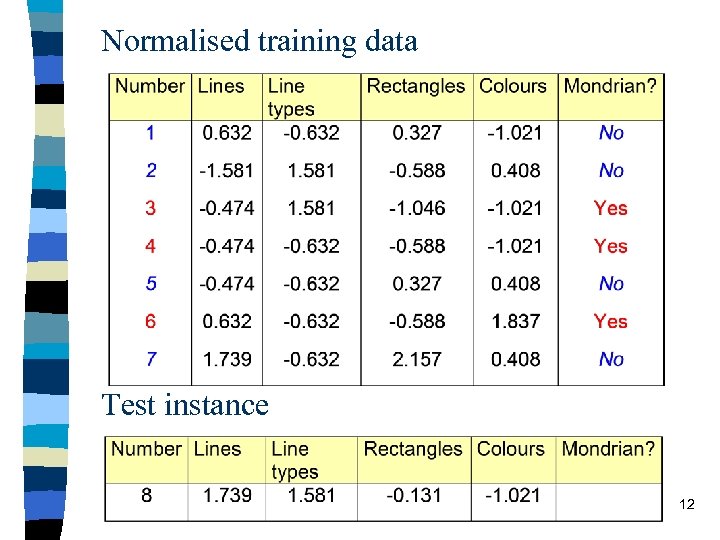
Normalised training data Test instance 12
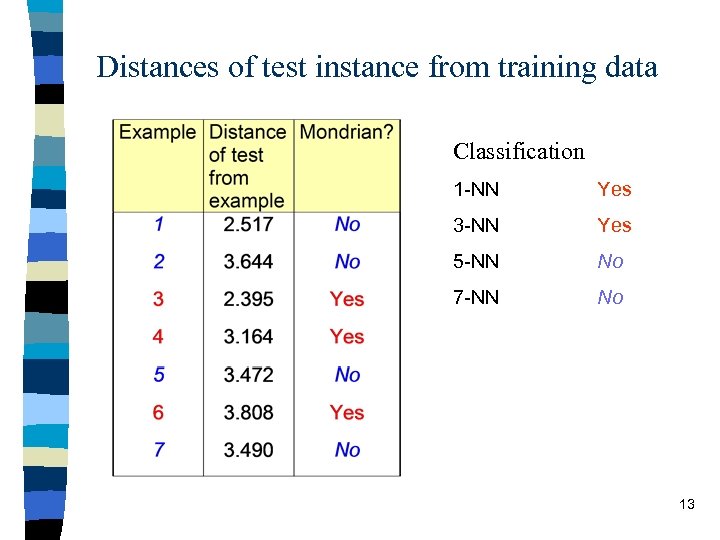
Distances of test instance from training data Classification 1 -NN Yes 3 -NN Yes 5 -NN No 7 -NN No 13

What if the target function is real valued? n The k-nearest neighbour algorithm would just calculate the mean of the k nearest neighbours 14

Variant of k. NN: Distance-Weighted k. NN n We might want to weight nearer neighbors more heavily n Then it makes sense to use all training examples instead of just k (Stepard’s method) 15

Difficulties with k-nearest neighbour algorithms n n Have to calculate the distance of the test case from all training cases There may be irrelevant attributes amongst the attributes – curse of dimensionality 16

Case-based reasoning (CBR) n n CBR is an advanced instance based learning applied to more complex instance objects Objects may include complex structural descriptions of cases & adaptation rules 17

n n n CBR cannot use Euclidean distance measures Must define distance measures for those complex objects instead (e. g. semantic nets) CBR tries to model human problem-solving – uses past experience (cases) to solve new problems – retains solutions to new problems n CBR is an ongoing area of machine learning research with many applications 18

Applications of CBR n Design – landscape, building, mechanical, conceptual design of aircraft sub-systems n Planning – repair schedules n Diagnosis – medical n Adversarial reasoning – legal 19
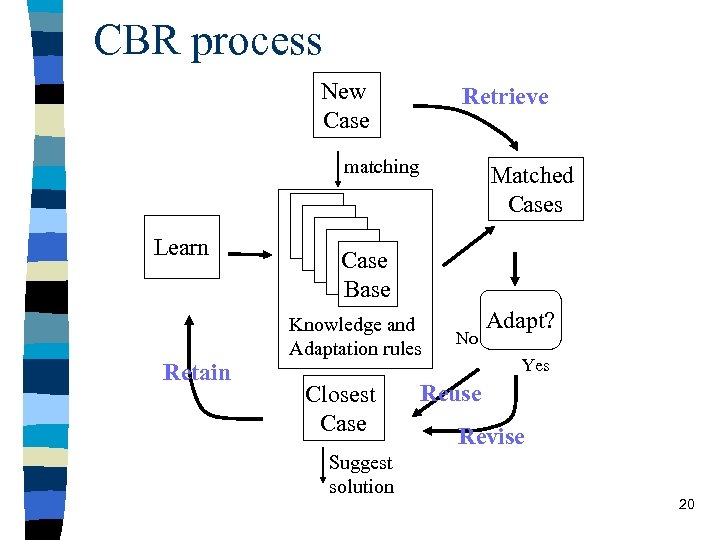
CBR process New Case Retrieve matching Learn Retain Matched Cases Case Base Knowledge and Adaptation rules Closest Case Suggest solution No Adapt? Yes Reuse Revise 20
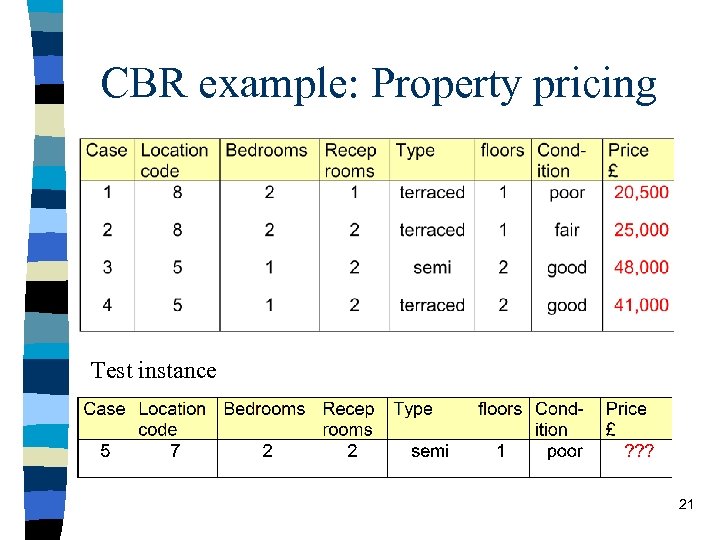
CBR example: Property pricing Test instance 21

How rules are generated n n There is no unique way of doing it. Here is one possibility: Examine cases and look for ones that are almost identical – case 1 and case 2 • R 1: If recep-rooms changes from 2 to 1 then reduce price by £ 5, 000 – case 3 and case 4 • R 2: If Type changes from semi to terraced then reduce price by £ 7, 000 22

Matching n Comparing test instance – matches(5, 1) = 3 – matches(5, 2) = 3 – matches(5, 3) = 2 – matches(5, 4) = 1 n Estimate price of case 5 is £ 25, 000 23

Adapting n Reverse rule 2 – if type changes from terraced to semi then increase price by £ 7, 000 n Apply reversed rule 2 – new estimate of price of property 5 is £ 32, 000 24

Learning n So far we have a new case and an estimated price – nothing is added yet to the case base n If later we find house sold for £ 35, 000 then the case would be added – could add a new rule • if location changes from 8 to 7 increase price by £ 3, 000 25

Problems with CBR n n How should cases be represented? How should cases be indexed for fast retrieval? How can good adaptation heuristics be developed? When should old cases be removed? 26

Advantages n n n A local approximation is found for each test case Knowledge is in a form understandable to human beings Fast to train 27

Summary n n n K-Nearest Neighbours Case-based reasoning Lazy and eager learning 28

Lazy and Eager Learning n Lazy: wait for query before generalizing – k-Nearest Neighbour, Case based reasoning n Eager: generalize before seeing query – Radial Basis Function Networks, ID 3, … n Does it matter? – Eager learner must create global approximation – Lazy learner can create many local approximations 29
aba63d6bcdead89b842ada0f5b5c24d8.ppt