Innovative Finite Element Methods For Aeroelastic Analysis Compiled

Innovative Finite Element Methods For Aeroelastic Analysis Compiled by: Roberto Flores* Presented by: Gabriel Bugeda* (*) CIMNE: International Center for Numerical Methods in Engineering, Barcelona, Spain MATEO ANTASME Meeting, 21/05/2007

Main Objectives of Task: • Analysis of thin walled structures with little or no bending stiffness subject to unsteady aerodynamic loads • Development of efficient FE techniques for the nonlinear (large strain & large displacement) analysis of membrane behavior, including wrinkling effects • Improvements to FE flow solvers to allow for fast solution of complex flow patterns • Robust coupling of structural solver and CFD codes for aeroelastic analysis

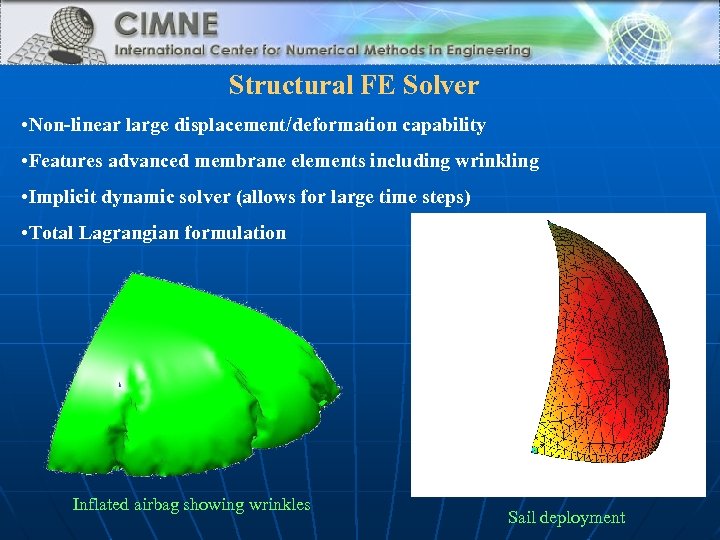Structural FE Solver • Non-linear large displacement/deformation capability • Features advanced membrane elements including wrinkling • Implicit dynamic solver (allows for large time steps) • Total Lagrangian formulation Inflated airbag showing wrinkles Sail deployment

CFD Solvers (I) Implicit incompressible solver for low speed flows • ALE formulation: Allows for mesh deformation • Orthogonal subgrid subscale stabilization: Technique developed at CIMNE. Achieves stabilization with minimum numerical diffusion by using assumed forms for unresolved flow scales • Choice of: • Second-Order Accurate Fractional Step (pressure segregated) solver • Monolithic solver

CFD Solvers (II) Explicit compressible solver for high speed flows • Edge-based data structure for minimum memory footprint and optimum performance • Second order space accuracy • Explicit multistage Runge-Kutta time integration scheme • Convective stabilization through limited upwinding • Implicit residual smoothing for convergence acceleration • Parallel execution on shared memory architectures via OPEN -MP directives

Edge oriented data structure NS equations in conservative form Approximate solution using FE discretization Weak semi-discrete form of the NS equations

The same finite element interpolation is used for fluxes: Solving for the nodal unknowns yields: The coefficients dij and bij are non-zero only for pairs nodes connected by an edge ( i. e. nodes belonging to the same element). The resulting algorithm is equivalent to a finite volume scheme in which the interface flux is the average of the nodal values of the edge. Furthermore, for any interior node: thus, the scheme is conservative because the total contribution of internal edges to the residual is zero.

The basic scheme is equivalent to a centered finite difference stencil which is inherently unstable due to the odd-even decoupling phenomenon. The interface fluxes are modified according to Roe’s upwind scheme in order to suppress instabilities: The factor k controls the extrapolation order for the interface fluxes, which can range from first to third order. The coefficients si represent the flux limiters which revert the scheme to first order near discontinuities and sharp gradients. In areas where the flow field is smooth the high order scheme is used instead. The limiters are calculated from the ratio of the solution gradients at the ends of the edge.

Coupled Euler+Boundary Layer Solver • Solution of viscous problems at high Re numbers requires use of turbulence models and hybrid meshes to resolve the boundary layer • Preparation of a suitable mesh is a lengthy task which cannot be easily automated • To reduce computational costs and speed up the preprocessing stage a coupled Euler+Boundary Layer solved has been developed • Uses boundary mesh of 3 D volume to create a “virtual” hybrid boundary layer mesh (extruded prisms) • In order to capture 3 D effects no integral solution is sought, 3 D boundary layer equations are solved directly • Mapping of arbitrary 3 D surface to a plane using unstructured surface mesh considered too involved Flux balances calculated in global coordinate system and projected to local curvilinear coordinates at each point. • Cell-centered finite volume scheme • Boundary layer solution coupled to external inviscid flow through transpiration boundary conditions

Finite Volume Discretization “Virtual” boundary layer cell Cj Ci ni h lij nj nij Outer boundary of Euler 3 D mesh The flow of a conservative variable from cell i to cell j is then calculated as:

Solution scheme for boundary layer equations Solve approximate momentum equation in global coordinate system Remove normal component Correct momentum using continuity equation n This integral is calculated establishing the mass balance for the cell

Coupling of boundary layer solution with external flow Determine displacement thickness * and evaluate transpiration velocity Remarks: • As the boundary layer thickness is replaced with a transpiration velocity, the Euler mesh does not need to be replaced • The scheme is not self-starting, for cells around a stagnation point a similarity solution for the flow near a stagnation area is used • The FV scheme is cell centered whereas the FE algorithm is vertex centered, the variables can by transferred by means of:

Coupled Fluid-Structural Solver • CIMNE’s Kratos multiphysics development framework enables coupling of CFD solver with a FEA structural code to analyze dynamic fluidstructure coupling phenomena • KRATOS has been completely developed in C++ using a modular objectoriented data structure to enable efficient coupling of single field solvers in a straightforward way • Features a Python-Based programmable input • Available coupling strategies: • STRONG COUPLING: “SAFE” but often computationally expensive, requires iterative solving strategy • LOOSE COUPLING: Often considered “UNSAFE”, computational efficiency is potentially very HIGH

Coupled Fluid-Structure Interaction Problem Structural Deformation Change in fluid Boundary conditions Change in the pressure field • Boundary conditions for the fluid are not known until the structure displacement is calculated BUT • Loads on the structure cannot be determined until the flow field has been solved for

Coupled “Fractional Step” Strategy • Structural Prediction is done by SOLVING the structure subject to a predicted pressure field (the simplest choice is the pressure at the end of the previous step) • Mesh movement step • Fluid Solution • Structural Correction It follows the same rationale as the fractional step (pressure segregation) procedures used for the solution of the Navier. Stokes equations

Error due to the coupling algorithm Assuming that the pressure can be described in the form and that the structural time integrator can be expressed in a form of the type it is possible to express the solution of the coupled problem as where yn is an error term, for the coupling procedure to be stable this term must not grow without bounds The amplification factor of the error term is Convergence is achieved when this factor is less than one

Remark: The amplification factor does not depend on the particular time integration scheme selected The basic scheme: can be replaced with the procedure remains consistent, as there is no change when Δt→ 0 Inserting the assumed form of the pressure into the modified algorithm we have now the scheme is stable when

• By choosing an appropriate value for irrespective of the mass ratio • A suitable value can be estimated from the structure of the stiffness matrix of the fluid problem the procedure can be made stable Remark: Fluid and structural meshes need not be congruent, therefore loads on the structure are calculated remapping the flow solution. Loads are transferred by means of: where NS and NF represent the shape functions for the structural and fluid meshes respectively. This is a conservative mapping scheme in the sense that energy conservation is preserved. Fvon Karman = 3. 7 Hz Fcoupled simulation = 3. 05 Hz Fcoupled experiment = 3. 10 Hz Example: Flag Flutter

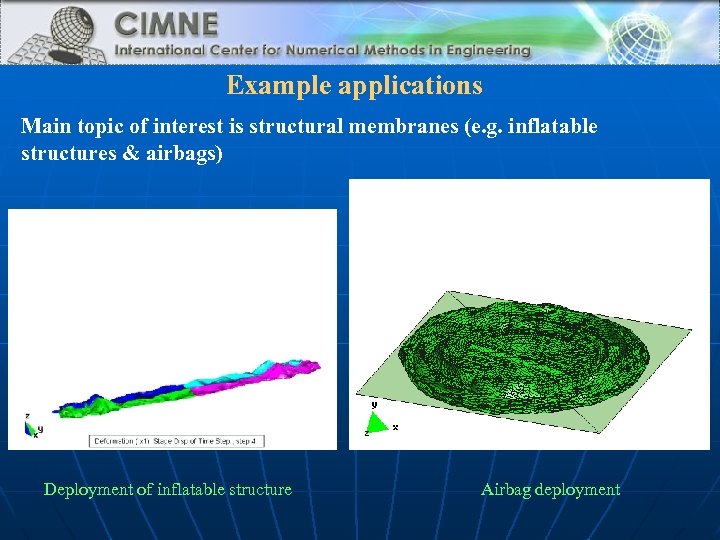Example applications Main topic of interest is structural membranes (e. g. inflatable structures & airbags) Deployment of inflatable structure Airbag deployment

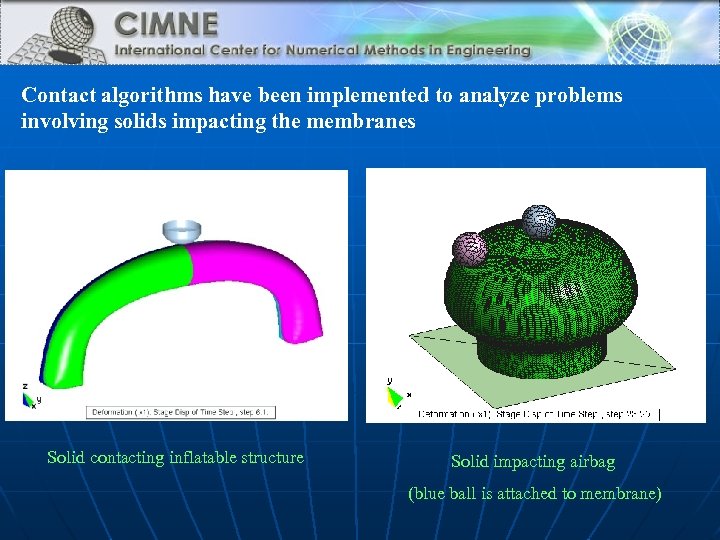Contact algorithms have been implemented to analyze problems involving solids impacting the membranes Solid contacting inflatable structure Solid impacting airbag (blue ball is attached to membrane)

Thank you for your attention