Injection Locked Oscillators Optoelectronic Applications Q 1 ω

Injection Locked Oscillators Optoelectronic Applications Q 1, ω 1 Q 2, ω 2 E. Shumakher, J. Lasri, B. Sheinman, G. Eisenstein, D. Ritter Electrical Engineering Dept. TECHNION Haifa ISRAEL

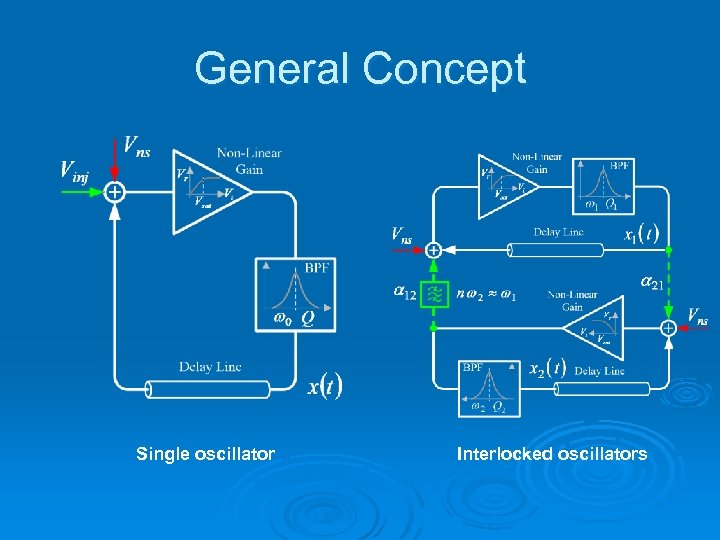General Concept Single oscillator Interlocked oscillators

Fundamental Locking First formulated by R. Adler (1946) Principal locking criteria Given a master oscillator, coupled unidirectionally to a slave oscillator with Locking takes place within the locking range

Harmonic Locking Ø Two possible configurations Sub-harmonic injection locking : Super-harmonic injection locking : Ø Consequences l l l Injected signal does not satisfy Lifetime is very short inside the oscillating loop Dynamics of the loop can not be altered

Harmonic Locking requires mediation by a non-linearity Harmonics generation – Mixing with harmonics creates a component at slave oscillator and which locks the

Unidirectional Locking Ø l l Improved signal quality Superharmonic IL – further improvement or Ø l l Synchronization – Timing extraction Harmonic IL – Multirate timing extraction

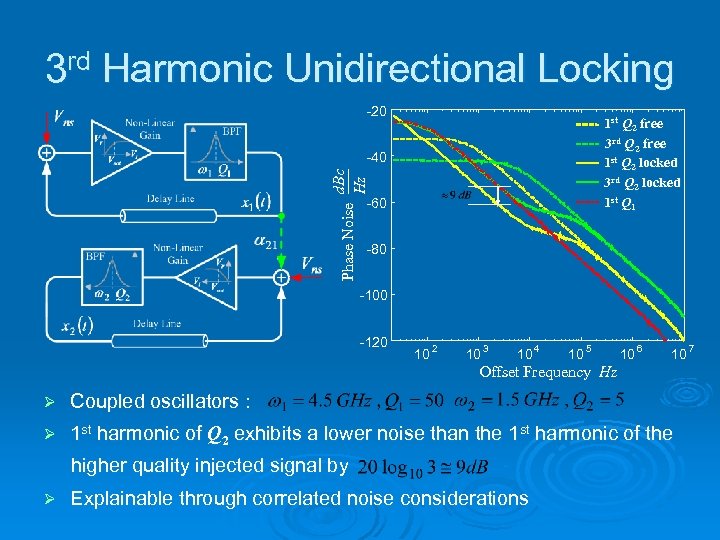3 rd Harmonic Unidirectional Locking -20 1 st Q 2 free 3 rd Q 2 free 1 st Q 2 locked 3 rd Q 2 locked 1 st Q 1 Phase Noise d. Bc Hz -40 -60 -80 -100 -120 10 2 10 3 10 4 10 5 10 6 10 Offset Frequency Hz Ø Coupled oscillators : Ø 1 st harmonic of Q 2 exhibits a lower noise than the 1 st harmonic of the higher quality injected signal by Ø Explainable through correlated noise considerations 7

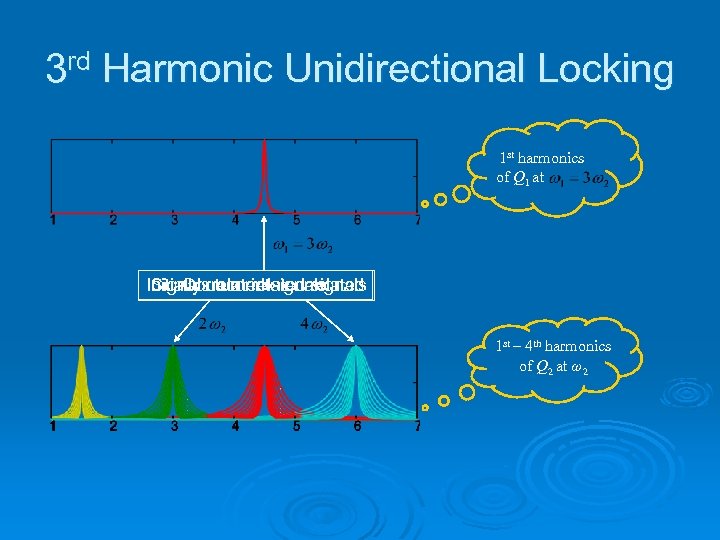3 rd Harmonic Unidirectional Locking 1 st harmonics of Q 1 at Correlated signals Initially uncorrelated signals Signals turn into correlated 1 st – 4 th harmonics of Q 2 at ω2

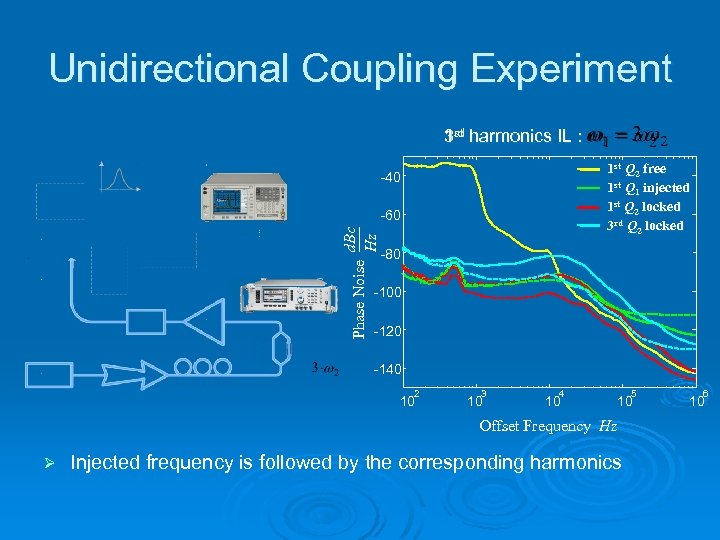Unidirectional Coupling Experiment 3 rd harmonics IL : 1 st Q 2 free 1 st Q 1 injected 1 st Q 2 locked 3 rd Q 2 locked -40 Phase Noise d. Bc Hz -60 -80 -100 -120 -140 2 10 3 10 4 10 Offset Frequency Hz Ø 5 10 Injected frequency is followed by the corresponding harmonics 6 10

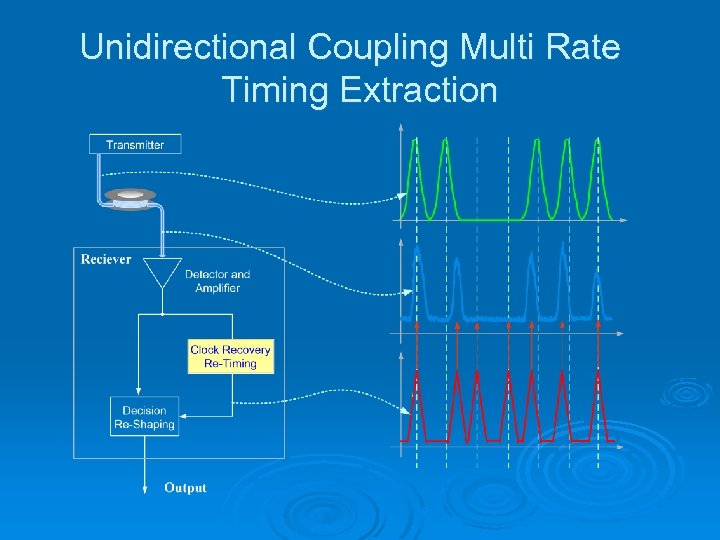Unidirectional Coupling Multi Rate Timing Extraction

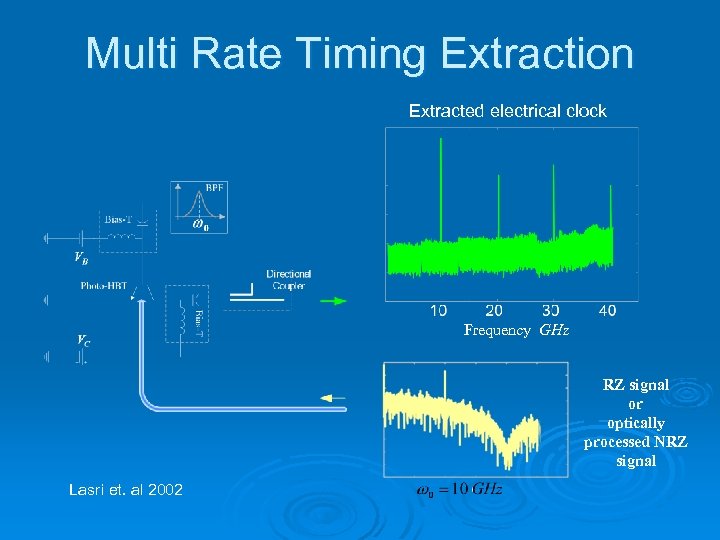Multi Rate Timing Extraction Extracted electrical clock Frequency GHz RZ signal or optically processed NRZ signal Lasri et. al 2002

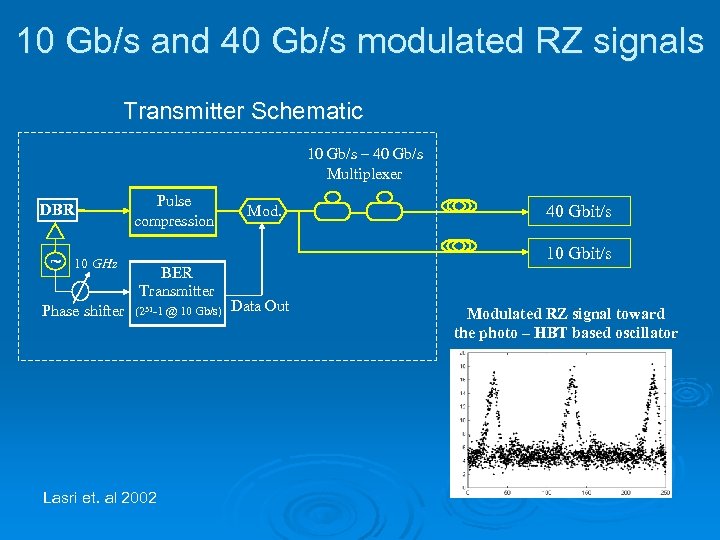10 Gb/s and 40 Gb/s modulated RZ signals Transmitter Schematic 10 Gb/s – 40 Gb/s Multiplexer Pulse compression DBR ~ 10 GHz Phase shifter Mod. 40 Gbit/s 10 Gbit/s BER Transmitter (231 -1 @ 10 Gb/s) Lasri et. al 2002 Data Out Modulated RZ signal toward the photo – HBT based oscillator

Clock recovery of RZ data by direct optical IL of Photo-HBT based oscillator Recovered Clock Lasri et. al 2002

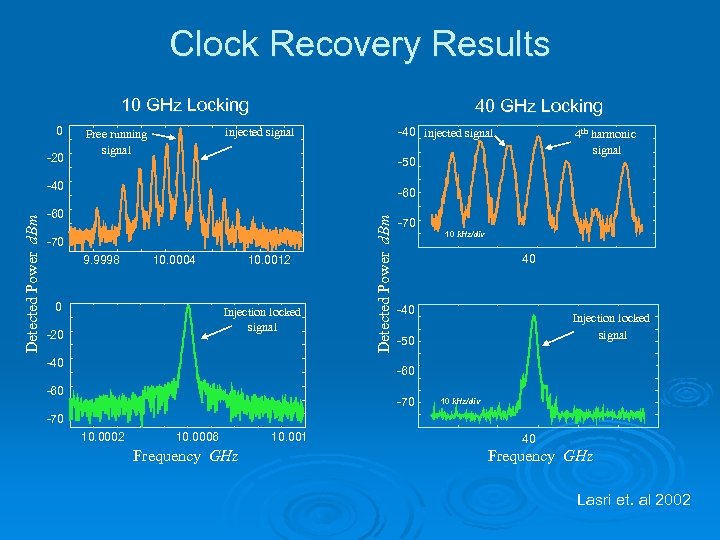Clock Recovery Results 10 GHz Locking 0 -20 40 GHz Locking -40 injected signal Free running signal -50 -40 -60 -70 9. 9998 10. 0004 0 10. 0012 Injection locked signal -20 -40 Detected Power d. Bm 4 th harmonic signal -70 10 k. Hz/div 40 -40 Injection locked signal -50 -60 -70 10 k. Hz/div -70 10. 0002 10. 0006 Frequency GHz 10. 001 40 Frequency GHz Lasri et. al 2002

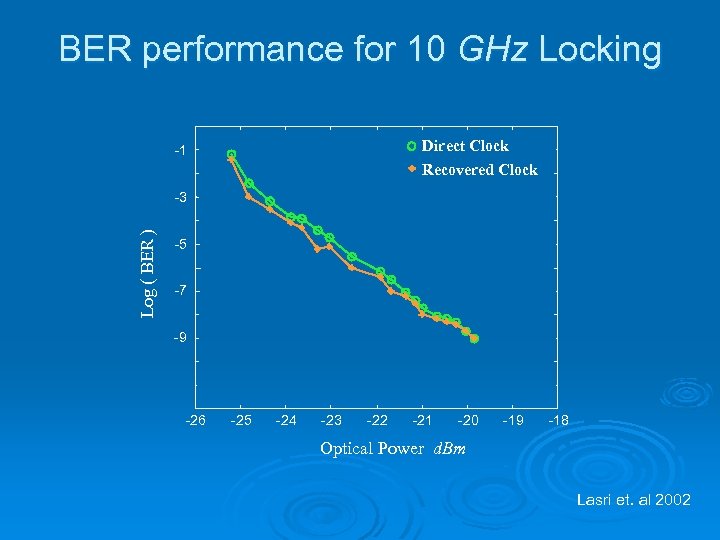BER performance for 10 GHz Locking Direct Clock -1 Recovered Clock Log ( BER ) -3 -5 -7 -9 -26 -25 -24 -23 -22 -21 -20 -19 -18 Optical Power d. Bm Lasri et. al 2002

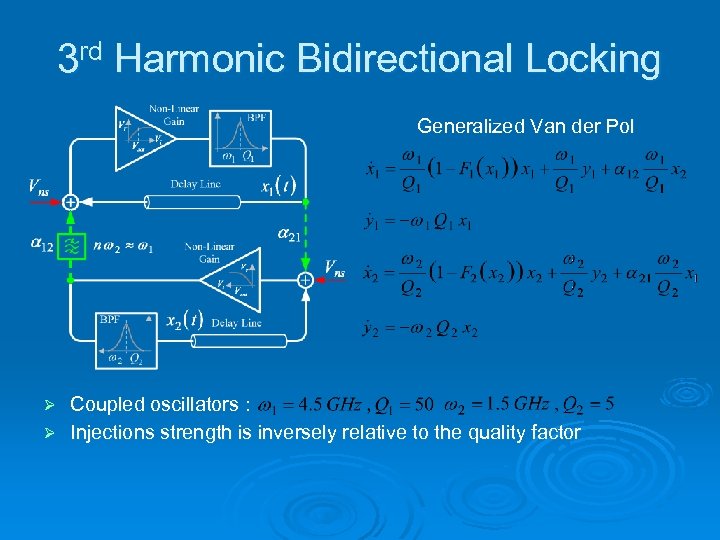3 rd Harmonic Bidirectional Locking Generalized Van der Pol Coupled oscillators : Ø Injections strength is inversely relative to the quality factor Ø

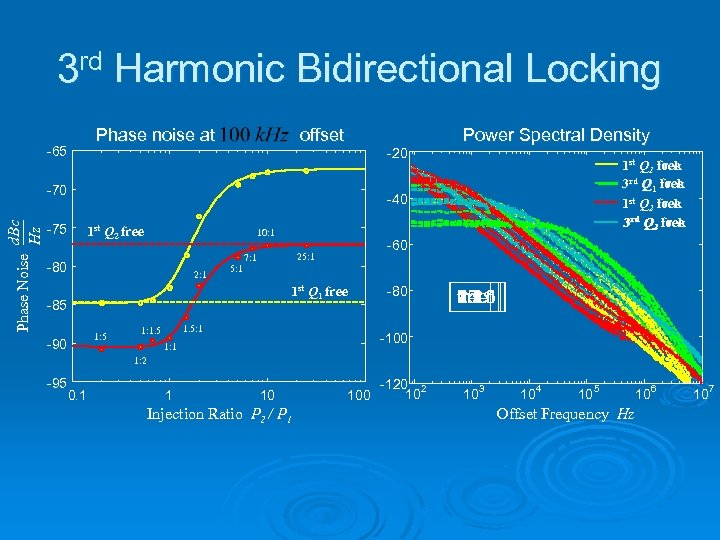3 rd Harmonic Bidirectional Locking Phase noise at -65 offset -20 Phase Noise d. Bc Hz -70 -75 Power Spectral Density 1 st Q 1 lock free 3 rd Q 1 lock free st Q lock 1 2 free 3 rd Q 2 lock 3 rd Q 2 free -40 1 st Q 2 free 10: 1 -80 2: 1 5: 1 -60 25: 1 7: 1 1 st Q 1 free -85 1: 5 -90 1. 5: 1 1: 1. 5 -80 1: 1. 5 25: 1 10: 1 7: 1 5: 1 1: 5 free 2: 1 1: 2 -100 1: 1 1: 2 -95 0. 1 1 10 Injection Ratio P 2 / P 1 100 -120 2 10 10 3 10 4 10 5 Offset Frequency Hz 10 6 10 7

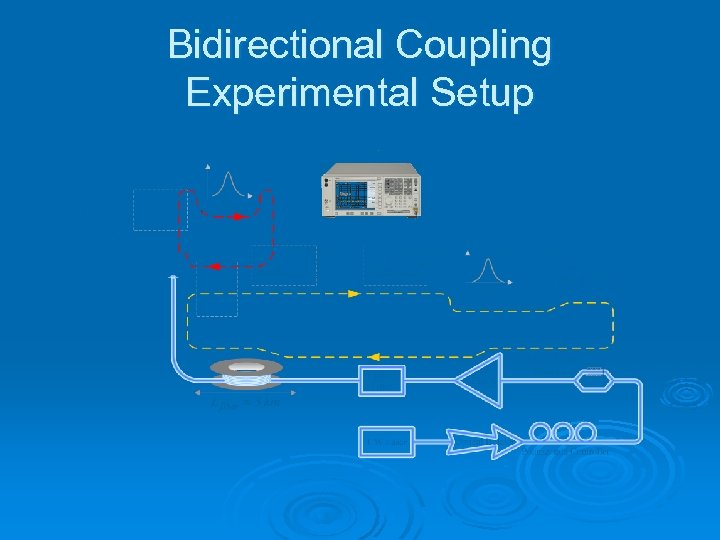Bidirectional Coupling Experimental Setup

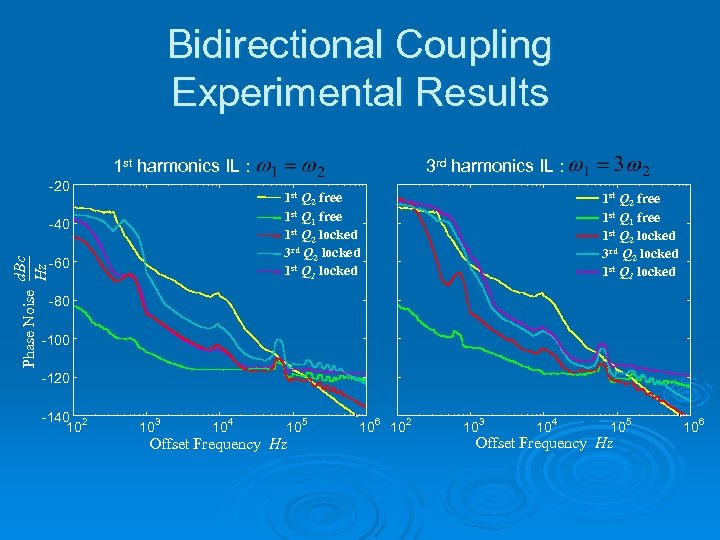Bidirectional Coupling Experimental Results 1 st harmonics IL : -20 1 st Q 2 free 1 st Q 1 free 1 st Q 2 locked 3 rd Q 2 locked 1 st Q 1 locked d. Bc Hz -40 -60 Phase Noise 3 rd harmonics IL : 1 st Q 2 free 1 st Q 1 free 1 st Q 2 locked 3 rd Q 2 locked 1 st Q 1 locked -80 -100 -120 -140 2 10 103 104 105 Offset Frequency Hz 106 102 103 104 105 Offset Frequency Hz 106

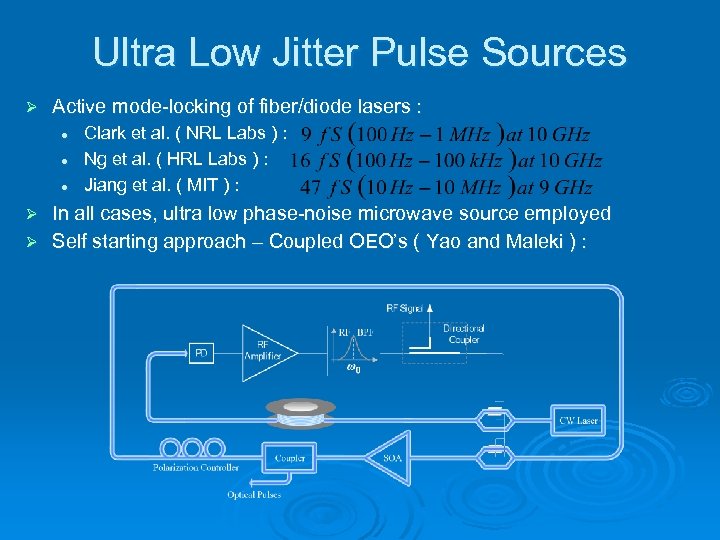Ultra Low Jitter Pulse Sources Ø Active mode-locking of fiber/diode lasers : l l l Clark et al. ( NRL Labs ) : Ng et al. ( HRL Labs ) : Jiang et al. ( MIT ) : In all cases, ultra low phase-noise microwave source employed Ø Self starting approach – Coupled OEO’s ( Yao and Maleki ) : Ø

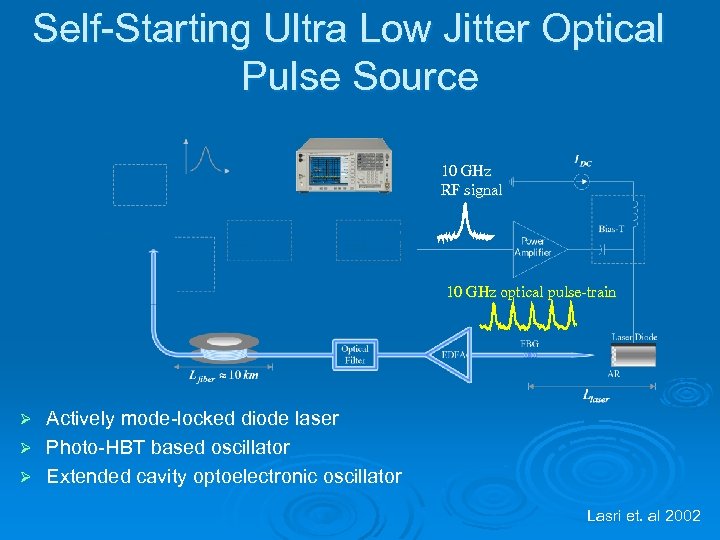Self-Starting Ultra Low Jitter Optical Pulse Source 10 GHz RF signal 10 GHz optical pulse-train Actively mode-locked diode laser Ø Photo-HBT based oscillator Ø Extended cavity optoelectronic oscillator Ø Lasri et. al 2002

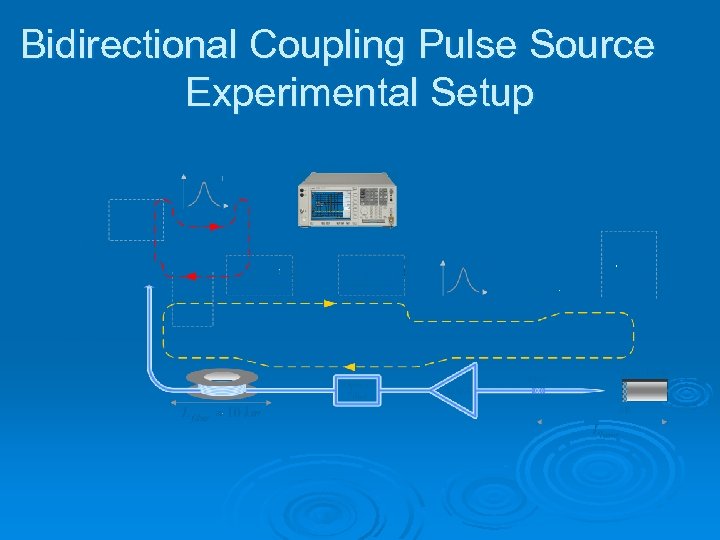Bidirectional Coupling Pulse Source Experimental Setup

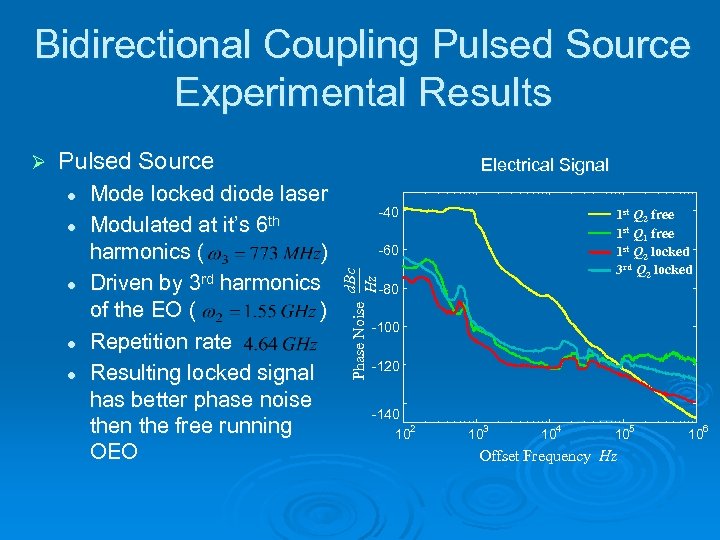Bidirectional Coupling Pulsed Source Experimental Results Pulsed Source l l Mode locked diode laser Modulated at it’s 6 th harmonics ( ) Driven by 3 rd harmonics of the EO ( ) Repetition rate Resulting locked signal has better phase noise then the free running OEO -40 1 st Q 2 free 1 st Q 1 free 1 st Q 2 locked 3 rd Q 2 locked -60 d. Bc Hz l Electrical Signal -80 Phase Noise Ø -100 -120 -140 102 3 10 4 10 5 10 Offset Frequency Hz 6 10

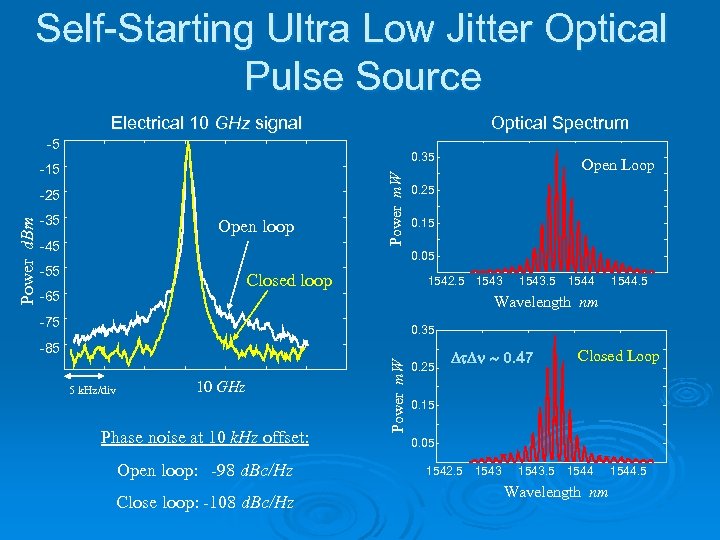Self-Starting Ultra Low Jitter Optical Pulse Source Electrical 10 GHz signal Optical Spectrum -5 -35 Open loop -45 Open Loop 0. 25 0. 15 0. 05 -55 Closed loop -65 1542. 5 1543. 5 1544. 5 Wavelength nm -75 0. 35 -85 5 k. Hz/div 10 GHz Phase noise at 10 k. Hz offset: Open loop: -98 d. Bc/Hz Close loop: -108 d. Bc/Hz Power m. W Power d. Bm -25 Power m. W 0. 35 -15 0. 25 Dt. Dn ~ 0. 47 Closed Loop 0. 15 0. 05 1542. 5 1543. 5 1544 Wavelength nm 1544. 5

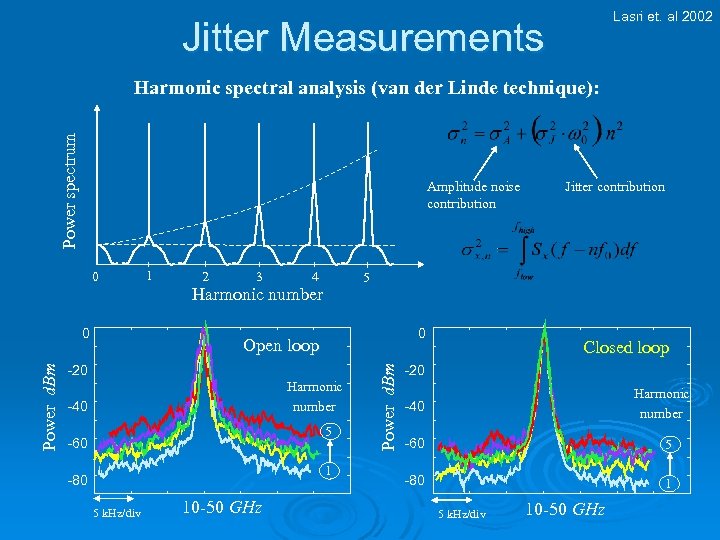Lasri et. al 2002 Jitter Measurements Power spectrum Harmonic spectral analysis (van der Linde technique): Amplitude noise contribution 0 1 2 3 4 5 Harmonic number 0 Open loop -20 Harmonic number -40 5 -60 1 -80 5 k. Hz/div 10 -50 GHz Power d. Bm 0 Jitter contribution Closed loop -20 Harmonic number -40 -60 5 -80 1 5 k. Hz/div 10 -50 GHz

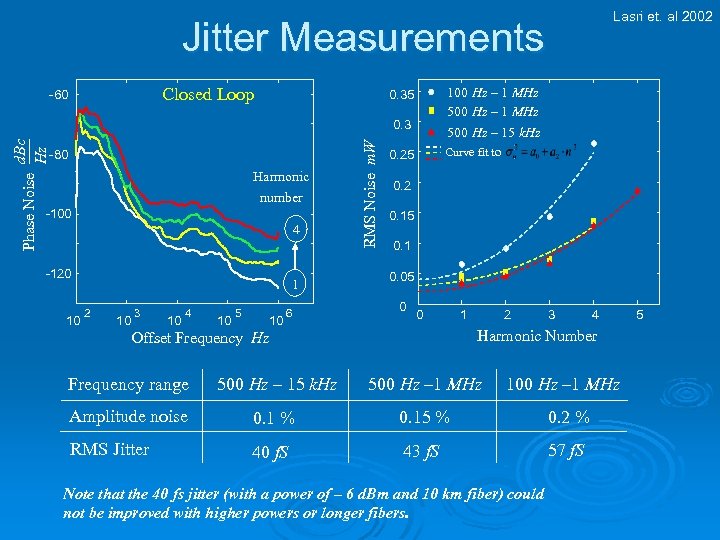Lasri et. al 2002 Jitter Measurements Closed Loop -60 100 Hz – 1 MHz 500 Hz – 15 k. Hz 0. 35 -80 Harmonic number -100 4 -120 10 1 2 10 3 10 4 10 5 10 6 RMS Noise m. W Phase Noise d. Bc Hz 0. 3 Curve fit to 0. 25 0. 2 0. 15 0. 1 0. 05 0 0 1 2 3 4 Harmonic Number Offset Frequency Hz Frequency range 500 Hz – 15 k. Hz 500 Hz – 1 MHz 100 Hz – 1 MHz Amplitude noise 0. 1 % 0. 15 % 0. 2 % RMS Jitter 40 f. S 43 f. S 57 f. S Note that the 40 fs jitter (with a power of – 6 d. Bm and 10 km fiber) could not be improved with higher powers or longer fibers. 5

Conclusion Ø Ø Ø Ø Photo HBT based oscillator – versatile multi functional system Accurate numerical model Fundamental and Harmonic injection locking Uni and bi-directional locking Improved noise performance due to correlated noise interaction in Harmonically locked oscillators Multi rate timing extraction Bi-directional locking – characteristics determined by mutual locking efficiency and relevant Q factors Self starting low jitter mode locked diode laser

Fundamental Locking The locking mechanism l Injected signal x 1 (t) saturates the gain l Loop lifetime is long l Free running dynamics are overwritten by x 1 (t) for

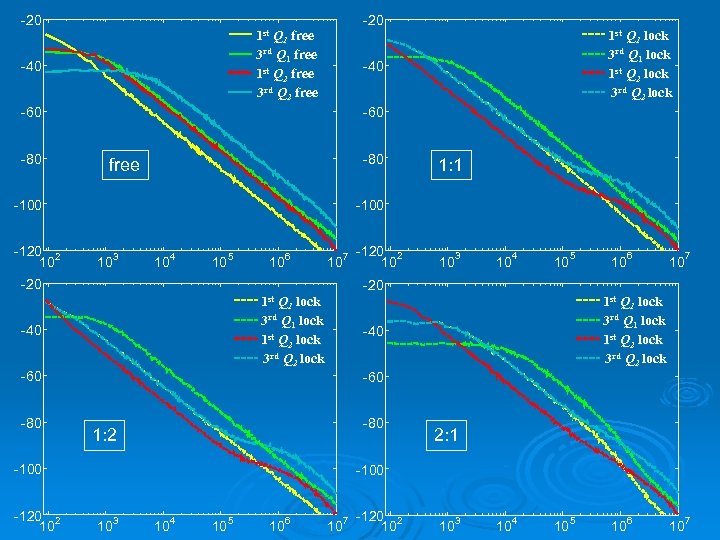-20 1 st Q 1 free 3 rd Q 1 free 1 st Q 2 free 3 rd Q 2 free -40 -60 -80 free 1: 1 -100 -120 2 10 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock 10 3 10 4 10 5 10 6 10 7 -20 -120 2 10 10 3 10 4 10 5 Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 10 7 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -60 -80 1: 2 -100 -120 2 10 6 -20 1 st -80 10 2: 1 -100 10 3 10 4 10 5 10 6 10 7 -120 2 10 10 3 10 4 10 5 10 6

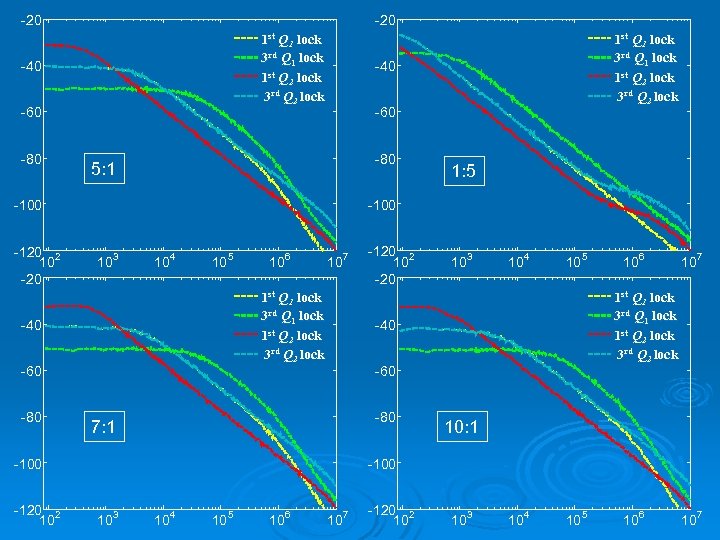-20 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -60 -80 5: 1 10 3 10 4 10 5 10 6 10 7 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -60 -80 -120 2 10 -20 10 3 10 4 10 5 -60 -80 7: 1 10 6 10 7 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -100 -120 2 10 1: 5 -100 -120 2 10 -20 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock 10: 1 -100 10 3 10 4 10 5 10 6 10 7 -120 2 10 10 3 10 4 10 5 10 6

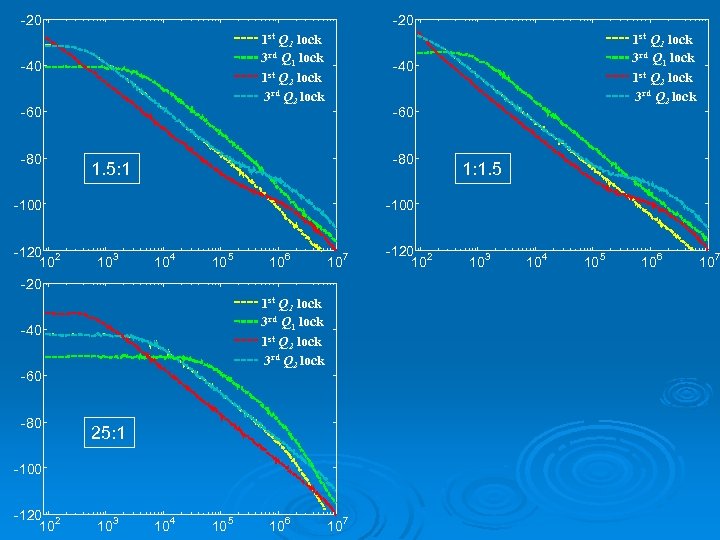-20 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -60 -80 1. 5: 1 10 3 10 4 10 5 10 6 10 7 -20 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock -40 -60 -80 25: 1 -100 -120 2 10 1: 1. 5 -100 -120 2 10 1 st Q 1 lock 3 rd Q 1 lock 1 st Q 2 lock 3 rd Q 2 lock 10 3 10 4 10 5 10 6 -120 2 10 10 3 10 4 10 5 10 6 10 7

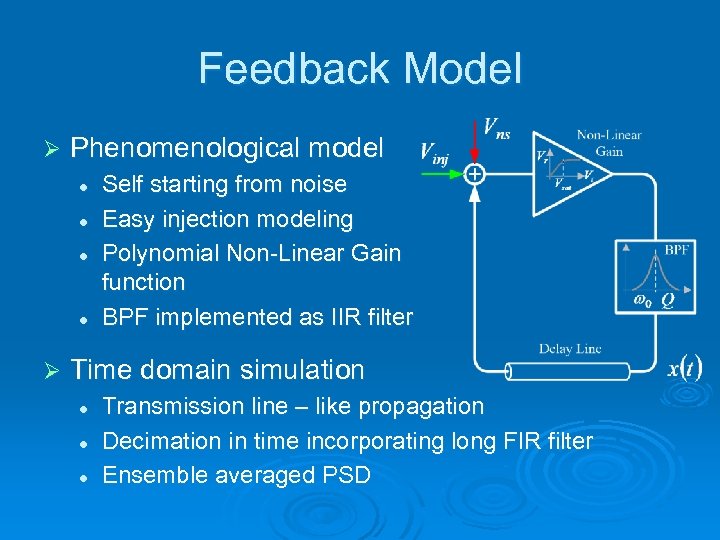Feedback Model Ø Phenomenological model l l Ø Self starting from noise Easy injection modeling Polynomial Non-Linear Gain function BPF implemented as IIR filter Time domain simulation l l l Transmission line – like propagation Decimation in time incorporating long FIR filter Ensemble averaged PSD

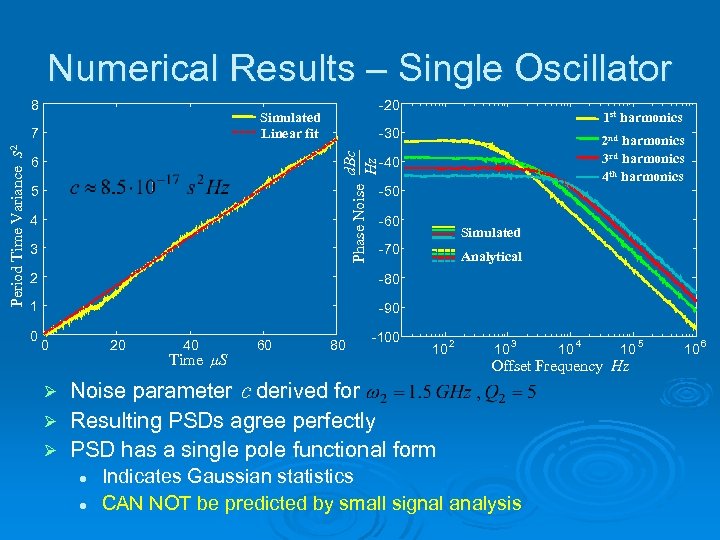Numerical Results – Single Oscillator 8 d. Bc Hz 6 1 st harmonics -30 2 nd harmonics 3 rd harmonics 4 th harmonics -40 Phase Noise s 2 7 Period Time Variance -20 Simulated Linear fit -50 5 4 3 -60 Simulated -70 2 -80 1 Analytical -90 0 0 20 40 Time μS 60 80 -100 10 2 10 3 Noise parameter c derived for Ø Resulting PSDs agree perfectly Ø PSD has a single pole functional form l 4 10 Offset Frequency Hz Ø l 10 Indicates Gaussian statistics CAN NOT be predicted by small signal analysis 5 10 6