Information Rates for Two-Dimensional ISI Channels Jiangxin Chen

Information Rates for Two-Dimensional ISI Channels Jiangxin Chen and Paul H. Siegel Center for Magnetic Recording Research University of California, San Diego DIMACS Workshop March 22 -24, 2004 3/23/04 1

Outline • • Motivation: Two-dimensional recording Channel model Information rates Bounds on the Symmetric Information Rate (SIR) • Upper Bound • • Lower Bound • Convergence 3/23/04 Alternative upper bound Numerical results Conclusions DIMACS Workshop 2

Two-Dimensional Channel Model • Constrained input array • Linear intersymbol interference • Additive, i. i. d. 3/23/04 Gaussian noise DIMACS Workshop 3

Two-Dimensional Processes • Input process: • Output process: • Array upper left corner: lower right corner: 3/23/04 DIMACS Workshop 4

Entropy Rates • Output entropy rate: • Noise entropy rate: • Conditional entropy rate: 3/23/04 DIMACS Workshop 5

Mutual Information Rates • Mutual information rate: • Capacity: • Symmetric information rate (SIR): Inputs are constrained to be independent, identically distributed, and equiprobable binary. 3/23/04 DIMACS Workshop 6

Capacity and SIR • The capacity and SIR are useful measures of the achievable storage densities on the twodimensional channel. • They serve as performance benchmarks for channel coding and detection methods. • So, it would be nice to be able to compute them. 3/23/04 DIMACS Workshop 7

Finding the Output Entropy Rate • For one-dimensional ISI channel model: and where 3/23/04 DIMACS Workshop 8

Sample Entropy Rate • If we simulate the channel N times, using inputs with specified (Markovian) statistics and generating output realizations then converges to 3/23/04 with probability DIMACS Workshop 1 as . 9

Computing Sample Entropy Rate • The forward recursion of the sum-product (BCJR) algorithm can be used to calculate the probability of a sample realization of the channel output. • In fact, we can write where the quantity is precisely the normalization constant in the (normalized) forward recursion. 3/23/04 DIMACS Workshop 10

Computing Entropy Rates • Shannon-Mc. Millan-Breimann theorem implies as , where is a single long sample realization of the channel output process. 3/23/04 DIMACS Workshop 11

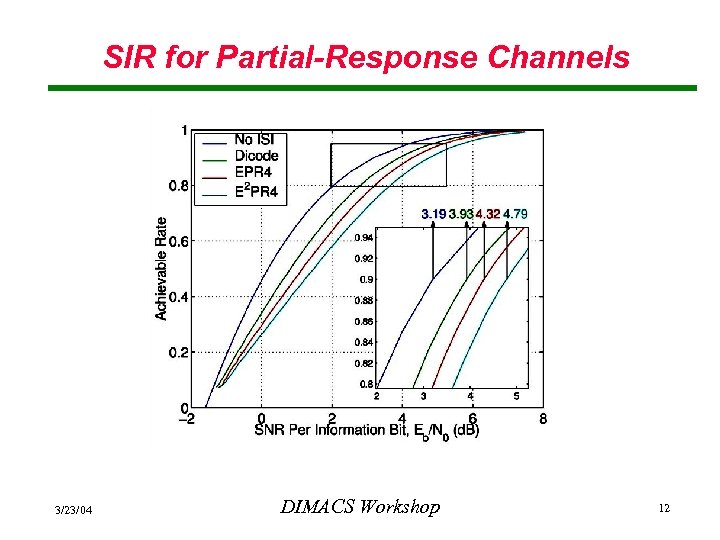SIR for Partial-Response Channels 3/23/04 DIMACS Workshop 12

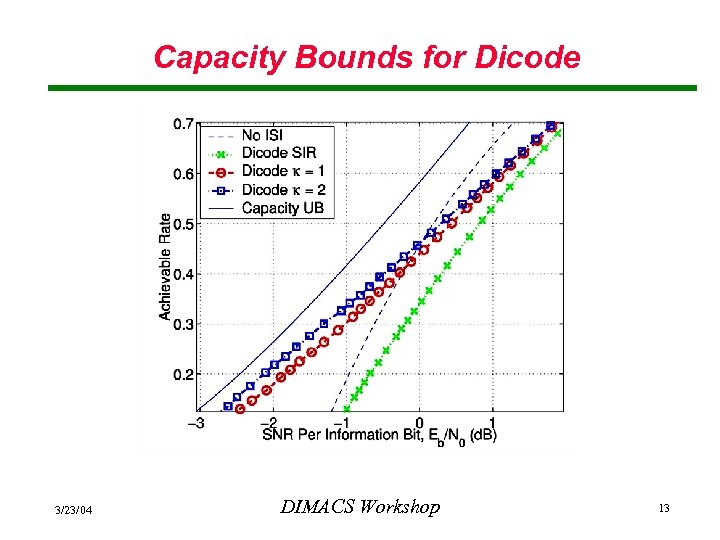Capacity Bounds for Dicode 3/23/04 DIMACS Workshop 13

Markovian Sufficiency Remark: It can be shown that optimized Markovian processes whose states are determined by their previous r symbols can asymptotically achieve the capacity of finite-state intersymbol interference channels with AWGN as the order r of the input process approaches . (J. Chen and P. H. Siegel, ISIT 2004) 3/23/04 DIMACS Workshop 14

Capacity and SIR in Two Dimensions • In two dimensions, we could estimate by calculating the sample entropy rate of a very large simulated output array. • However, there is no counterpart of the BCJR algorithm in two dimensions to simplify the calculation. • Instead, we use conditional entropies to derive upper and lower bounds on 3/23/04 . DIMACS Workshop 15

Array Ordering • Permuted lexicographic ordering: • Choose vector , a permutation of • Map each array index to • Then or precedes and . . if . • Therefore, row-by-row ordering column-by-column ordering 3/23/04 DIMACS Workshop 16

Two-Dimensional “Past” • Let vector. • Define preceding be a non-negative to be the elements inside the region (with permutation k ) 3/23/04 DIMACS Workshop 17

Examples of Past{Y[i, j]} 3/23/04 DIMACS Workshop 18

Conditional Entropies • For a stationary two-dimensional random field Y on the integer lattice, the entropy rate satisfies: (The proof uses the entropy chain rule. See [5 -6]) • This extends to random fields on the hexagonal lattice, via the natural mapping to the integer lattice. 3/23/04 DIMACS Workshop 19

Upper Bound on H(Y) • For a stationary two-dimensional random field Y, where 3/23/04 DIMACS Workshop 20

Two-Dimensional Boundary of Past{Y[i, j]} • Define of to be the boundary. • The exact expression for is messy, but the geometrical concept is simple. 3/23/04 DIMACS Workshop 21

Two-Dimensional Boundary of Past{Y[i, j]} 3/23/04 DIMACS Workshop 22

Lower Bound on H(Y) • For a stationary two-dimensional hidden Markov field Y, where and the strip 3/23/04 is the “state information” for. DIMACS Workshop 23

Sketch of Proof • Upper bound: Note that and that conditioning reduces entropy. • Lower bound: Markov property of information” 3/23/04 , given “state. DIMACS Workshop 24

Convergence Properties • The upper bound on the entropy rate is monotonically non-increasing as the size of the array defined by increases. • The lower bound on the entropy rate is monotonically non-decreasing as the size of the array defined by increases. 3/23/04 DIMACS Workshop 25

Convergence Rate • The upper bound and lower bound converge to the true entropy rate as fast as 3/23/04 O(1/lmin) , at least where DIMACS Workshop 26

Computing the SIR Bounds • Estimate the two-dimensional conditional entropies over a small array. • Calculate to get for many realizations of output array. • For column-by-column ordering, treat each row as a variable and calculate the joint probability row-by-row using the BCJR forward recursion. 3/23/04 DIMACS Workshop 27

2 x 2 Impulse Response • “Worst-case” scenario - large ISI: • Conditional entropies computed from 100, 000 realizations. • Upper bound: • Lower bound: (corresponds to element in middle of last column) 3/23/04 DIMACS Workshop 28

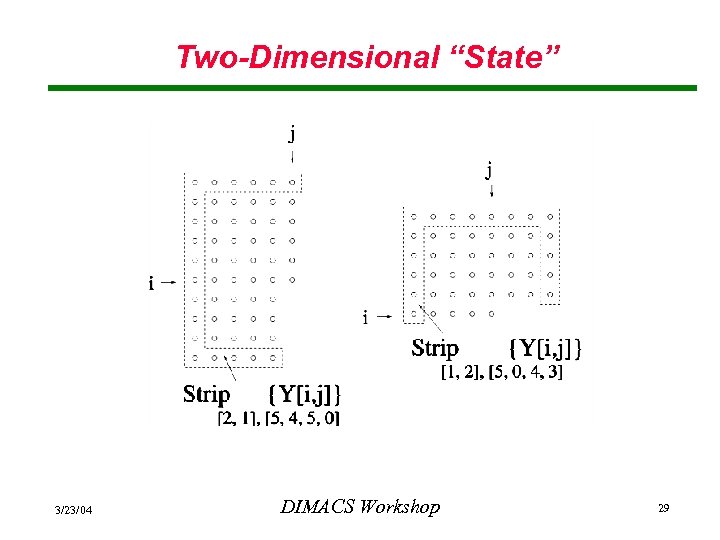Two-Dimensional “State” 3/23/04 DIMACS Workshop 29

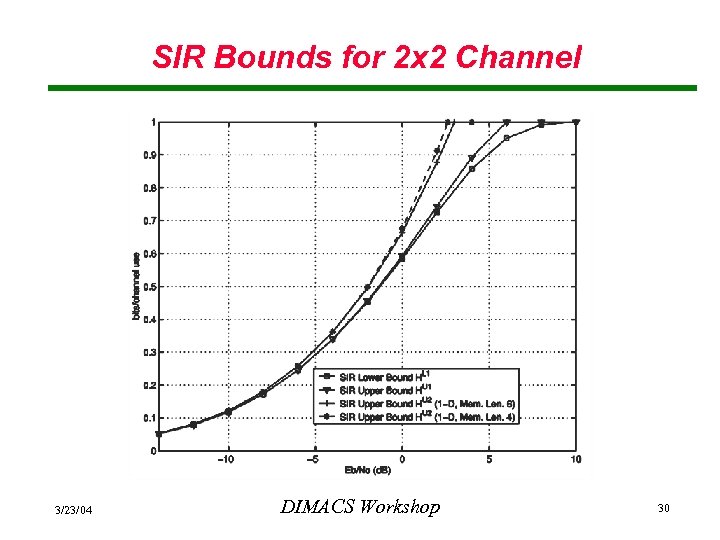SIR Bounds for 2 x 2 Channel 3/23/04 DIMACS Workshop 30

Computing the SIR Bounds • The number of states for each variable increases exponentially with the number of columns in the array. • This requires that the two-dimensional impulse response have a small support region. • It is desirable to find other approaches to computing bounds that reduce the complexity, perhaps at the cost of weakening the resulting bounds. 3/23/04 DIMACS Workshop 31

Alternative Upper Bound • Modified BCJR approach limited to small impulse response support region. • Introduce “auxiliary ISI channel” and bound where and is an arbitrary conditional probability distribution. 3/23/04 DIMACS Workshop 32

Choosing the Auxiliary Channel • Assume is conditional probability distribution of the output from an auxiliary ISI channel • A one-dimensional auxiliary channel permits a calculation based upon a larger number of columns in the output array. • Conversion of the two-dimensional array into a onedimensional sequence should “preserve” the statistical properties of the array. • Pseudo-Peano-Hilbert space-filling curves can be used on a rectangular array to convert it to a sequence. 3/23/04 DIMACS Workshop 33

Pseudo-Peano-Hilbert Curve 3/23/04 DIMACS Workshop 34

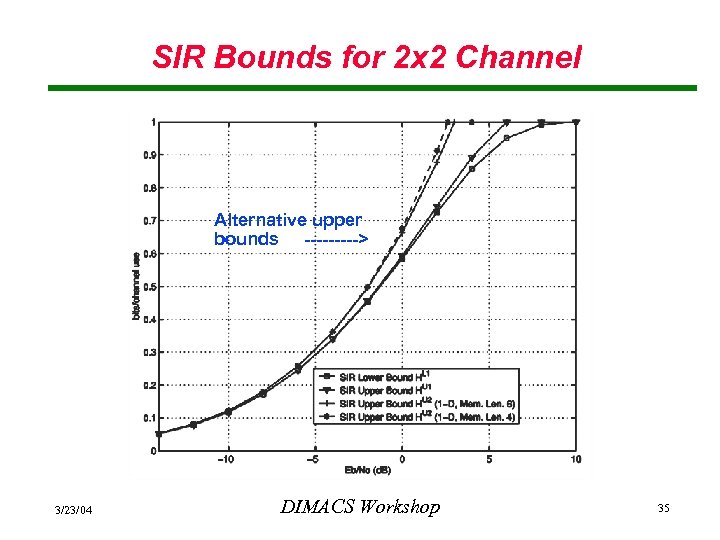SIR Bounds for 2 x 2 Channel Alternative upper bounds -----> 3/23/04 DIMACS Workshop 35

3 x 3 Impulse Response • Two-DOS transfer function • Auxiliary one-dimensional ISI channel with memory length 4. • Useful upper bound up to Eb/N 0 = 3 d. B. 3/23/04 DIMACS Workshop 36

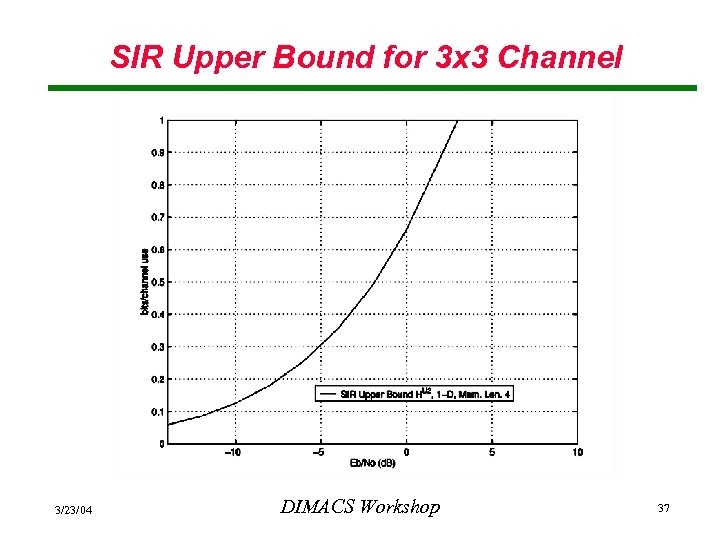SIR Upper Bound for 3 x 3 Channel 3/23/04 DIMACS Workshop 37

Concluding Remarks • Upper and lower bounds on the SIR of twodimensional finite-state ISI channels were presented. • Monte Carlo methods were used to compute the bounds for channels with small impulse response support region. • Bounds can be extended to multi-dimensional ISI channels • Further work is required to develop computable, tighter bounds for general multi-dimensional ISI channels. 3/23/04 DIMACS Workshop 38

References 1. 2. 3. 4. 5. D. Arnold and H. -A. Loeliger, “On the information rate of binaryinput channels with memory, ” IEEE International Conference on Communications, Helsinki, Finland, June 2001, vol. 9, pp. 2692 -2695. H. D. Pfister, J. B. Soriaga, and P. H. Siegel, “On the achievable information rate of finite state ISI channels, ” Proc. Globecom 2001, San Antonio, TX, November 2001, vol. 5, pp. 2992 -2996. V. Sharma and S. K. Singh, “Entropy and channel capacity in the regenerative setup with applications to Markov channels, ” Proc. IEEE International Symposium on Information Theory, Washington, DC, June 2001, p. 283. A. Kavcic, “On the capacity of Markov sources over noisy channels, ” Proc. Globecom 2001, San Antonio, TX, November 2001, vol. 5, pp. 2997 -3001. D. Arnold, H. -A. Loeliger, and P. O. Vontobel, “Computation of information rates from finite-state source/channel models, ” Proc. 40 th Annual Allerton Conf. Commun. , Control, and Computing, Monticello, IL, October 2002, pp. 457 -466. 3/23/04 DIMACS Workshop 39

References 6. 7. Y. Katznelson and B. Weiss, “Commuting measurepreserving transformations, ” Israel J. Math. , vol. 12, pp. 161 -173, 1972. D. Anastassiou and D. J. Sakrison, “Some results regarding the entropy rates of random fields, ” IEEE Trans. Inform. Theory, vol. 28, vol. 2, pp. 340 -343, March 1982. 3/23/04 DIMACS Workshop 40