32394c8150aa45eb5a2de9f083fccdc9.ppt
- Количество слайдов: 46

Information Layer Chapter 2. Binary Values and Number Systems Chapter 3. Data Representation

Digital System Digital system – All the information in digital system is represented as binary numbers (logically) • Base 2 with two digits: 0 & 1 (11010)2 = 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 = (26)10 Signals – These numbers are represented as electrical signals (physically) • Such as voltages – Two discrete values: high & low (or true & false, 1 & 0) • High 4. 0 V~5. 5 V • Low 0 V~1. 0 V

Electronic Signals Analog Signal – An analog signal continually fluctuates in time Digital Signal – Digital signal has only a high or low state Both analog and digital signals degrade as they move down a line due to a noise – This degradation is sometimes impossible to recover since there is no easy way to distinguish the noise from the signal. – However, digital signals can often be transmitted, stored and processed without introducing noise.
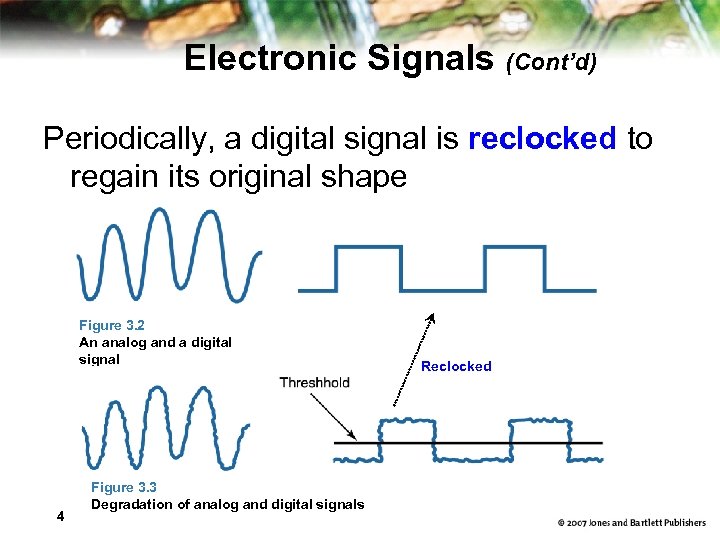
Electronic Signals (Cont’d) Periodically, a digital signal is reclocked to regain its original shape Figure 3. 2 An analog and a digital signal 4 Figure 3. 3 Degradation of analog and digital signals Reclocked

Digital System Bits and Bytes – Digits in a binary numbers are called bits • A binary digit is called a bit – A group of 8 bits is called a byte (B) • Byte is the basic unit of memory and storage – Information is represented in group of bits • Byte, KB (210), MB (220), GB (230), TB (240)
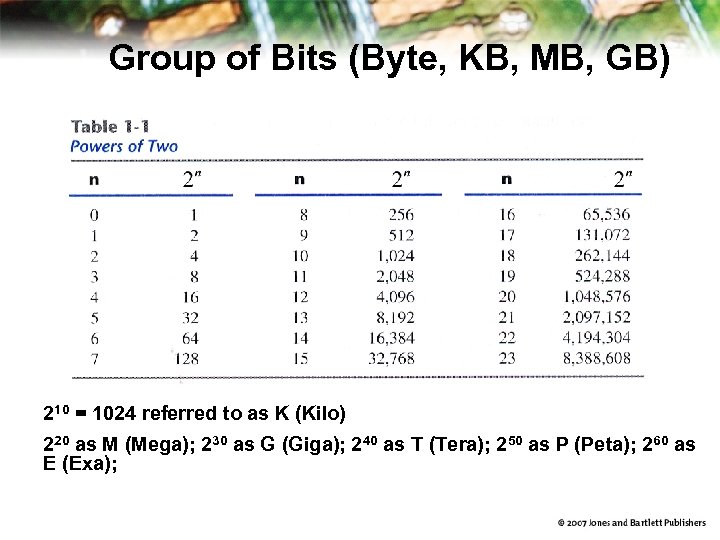
Group of Bits (Byte, KB, MB, GB) 210 = 1024 referred to as K (Kilo) 220 as M (Mega); 230 as G (Giga); 240 as T (Tera); 250 as P (Peta); 260 as E (Exa);

Number Systems Base-r (or radix r) system – Expressed with a power series in r where for all j – Positional notation • . is called radix point – an is the most significant digit • In binary, it is called the most significant bit (msb) – a-m is the least significant digit • In binary, it is called the least significant bit (lsb) – Enclose coefficients in parentheses and place a subscript (312. 4)5 = 3 x 52 + 1 x 51 + 2 x 50 + 4 x 5 -1 = 75 + 2 + 0. 8 = (82. 8)10 – In computers, binary, octal, and hexadecimal is popular.

Number Systems Octal numbers – Base 8 (0, 1, . . . , 6, 7) – 1 octal digit = 3 binary digits (001010111. 100)2 = (127. 4)8 = 1 x 82 + 2 x 81 + 7 x 80 + 4 x 8 -1 = (87. 5 )10 Hexadecimal numbers – Base 16 (0, 1, . . , 9, A, B, C, D, E, F) – 1 hexadecimal digit = 4 binary digits (1011011001011111)2 = (B 65 F)16 = x. B 65 F 11 x 163 + 6 x 162 + 5 x 161 + 15 x 160 = (46687)10
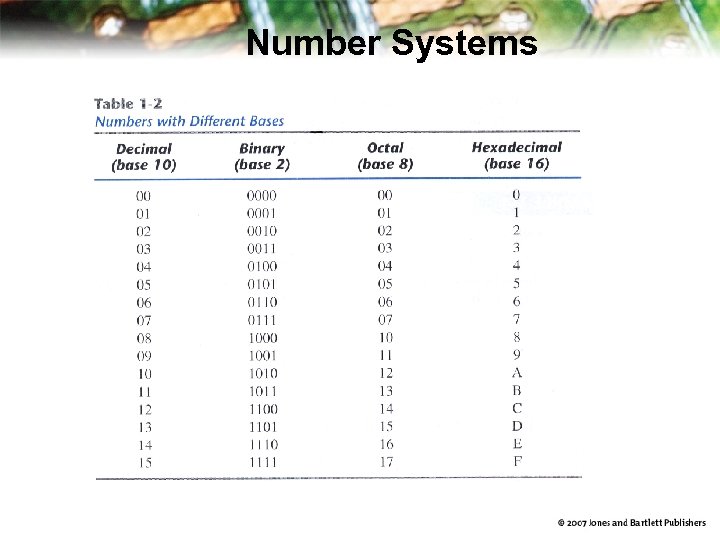
Number Systems

Arithmetic Operations Addition, subtraction, and multiplication – Same as for decimal numbers

Number Overflow What happen if the computed value won't fit? This is known as Overflow If each value is stored using seven bits, adding 127 to 3 overflows 1111111 + 0000011 10000010 Problems occur when mapping an infinite world onto a finite machine! 11

Number Base Conversion Binary to octal: – 10110001101011. 111100000110 = (26153. 7406)8 Binary to hexadecimal: – 10110001101011. 111100000110 = (2 C 6 B. F 06)16 Octal to binary: – (673. 124)8 = 11011. 001010100 Hexadecimal to binary: – (306. D)16 = 001100000110. 1101

Negative Numbers Two representative representations – Sign-magnitude – Two’s complement Sign-magnitude – Left most bit is sign bit and the remaining bits are magnitude. • 0 means positive • 1 means negative – Example • +5 = 00000101 • – 2 = 10000010 – Problems • Binary addition algorithm does not work for negative numbers • Two representations of zero (+0 and -0)

Complements – Represent negative numbers – Used for subtraction operation Two types of complements for base-r system – Radix complement: r’s complement – Diminished radix complement: (r – 1)’s complement r’s complement = rn – N (for an n-digit number N) – 2진수 n-bit 숫자 N에 대한 2의 보수는 2 n – N (r-1)’s complement = (rn – 1) – N – – 2진수 n-bit 숫자 N에 대한 1의 보수는 (2 n – 1) – N 1’s complements of 1011000 is 0100111 1’s complements of 0101101 is 1010010 따라서, 1의 보수는 N을 bit complement 한 것과 같음

2’s Complement Given N, 2’s complement of N with n bits – – 2 n – N = (2 n – 1) – N + 1 = bit complement of N + 1 Like sign-magnitude, MSB represents the sign bit 2’s complement can represent numbers from -2 n-1 to 2 n-1 +1 32 bit number • Positive numbers : 0 (x 0000) to 231 – 1 (x 7 FFFFFFF) • Negative numbers : -1 (x. FFFF) to – 231 (x 8000000) Examples – – – – +3 = 011 +2 = 010 +1 = 001 +0 = 000 -1 = 111 -2 = 110 -3 = 101 -4 = 100

Characteristics of 2’s Complement A single representation of zero Negation is fairly easy (bit complement of N + 1) – 3 – Boolean complement gives – Add 1 to LSB = 00000011 11111100 11111101 Arithmetic works easily – To perform A – B, take the 2’s complement of B and add it to A – A + (2 n – B) = A – B + 2 n (if A >= B, ignore the carry) = 2 n – (B – A) (if B > A, 2’s complement of B – A)

Real Numbers with fractions – 104. 32, 0. 999999, 357. 0, and 3. 14159 Binary real numbers – 1001. 1010 = 24 + 20 +2 -1 + 2 -3 =9. 625 Where is the binary point? Fixed-point (ex: integers) • Very large numbers cannot be represented • Very small fractions cannot be represented Floating-point • Use the exponent to slide (place) the binary point • 976, 000, 000 = 9. 76 * 1014 • 0. 000000976 = 9. 76 * 10 -14 17

Floating Point Number FP number can be represented by 3 components Sign bit – sign * mantissa (significand) * 2 exponent – Base 2 is omitted Exponent (E) Significand or Mantissa (S) – Multiple representations of a single number • 11. 101 can be represented by – 11. 101 * 20 – 1. 1101 * 21 (Normalized Representation) – 0. 1101 * 22 • Instead, normalized representation is used 18

Alphanumeric Codes Handle text of letters and numbers – Set of texts include 10 digits, 26 letters, special characters (+, -, *, /, =, <, etc. ) – if only capital letters: need 6 bits (36 ~ 64 letters) if upper/lower letters: need 7 bits (64 ~ 128 letters) ASCII character code – American Standard Code for Information Interchange – 7 -bit standard to represent 128 characters • ASCII contain 94 printable chars + 34 control chars – Later extended ASCII (8 -bit) evolved so that all eight bits were used
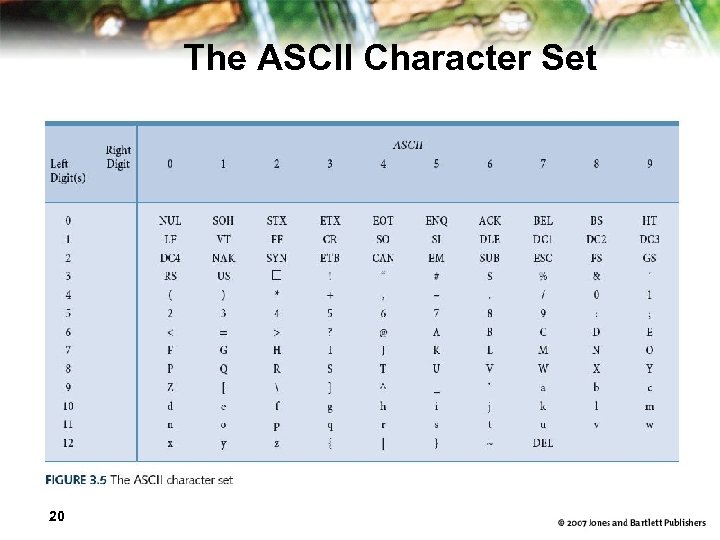
The ASCII Character Set 20

Unicode Extended ASCII is not enough for international use Unicode uses 16 bits per character – How many characters can Unicode represent? – The first 256 characters correspond exactly to the extended ASCII character set – The current standard uses 1 to 4 byte variable encoding and does not restrict to 16 -bit encoding • UTF-8 uses 8 -bit encoding – The first byte is ASCII and the remaining bytes are for other characters • UTF-16 uses 16 -bit encoding – The first 2 byte is UCS-2 21

The Unicode Character Set 22 Figure 3. 6 A few characters in the Unicode character set

Text Compression Assigning 16 bits to each character in a document uses too much file space We need ways to store and transmit text efficiently Text compression techniques Keyword encoding Run-length encoding Huffman encoding 23

Keyword Encoding Given the following paragraph, We hold these truths to be self-evident, that all men are created equal, that they are endowed by their Creator with certain unalienable Rights, that among these are Life, Liberty and the pursuit of Happiness. ム That to secure these rights, Governments are instituted among Men, deriving their just powers from the consent of the governed, ム That whenever any Form of Government becomes destructive of these ends, it is the Right of the People to alter or to abolish it, and to institute new Government, laying its foundation on such principles and organizing its powers in such form, as to them shall seem most likely to effect their Safety and Happiness. 24

Keyword Encoding Replace frequently used words with a single character 25

Keyword Encoding The encoded paragraph is We hold # truths to be self-evident, $ all men are created equal, $ ~y are endowed by ~ir Creator with certain unalienable Rights, $ among # are Life, Liberty + ~ pursuit of Happiness. — $ to secure # rights, Governments are instituted among Men, deriving ~ir just powers from ~ consent of ~ governed, — $ whenever any Form of Government becomes destructive of # ends, it is ~ Right of ~ People to alter or to abolish it, + to institute new Government, laying its foundation on such principles + organizing its powers in such form, ^ to ~m shall seem most likely to effect ~ir Safety + Happiness. 26

Keyword Encoding What did we save? Original paragraph 656 characters Encoded paragraph 596 characters Compression ratio 596/656 = 0. 9085 27

Run-Length Encoding A single character may be repeated over and over again in a long sequence Replace a repeated sequence with – a flag character – repeated character – number of repetitions *n 8 – * is the flag character – n is the repeated character – 8 is the number of times n is repeated 28

Run-Length Encoding Original text bbbbjjjkllqqqqqq+++++ Encoded text *b 8 jjjkll*q 6*+5 (Why isn't j encoded? ) The compression ratio is 15/25 or. 6 Encoded text *x 4*p 4 l*k 7 Original text xxxxpppplkkkkkkk 29

Huffman Encoding More frequently used letters should have shorter code to represent them – Why should the character “X” and “z” take up the same number of bits as “e” or “ ”? Huffman codes use variable-length bit strings to represent each character 30

Huffman Encoding ballboard would be 101001001010110001111011 compression ratio 28/72 31

Huffman Encoding • In Huffman encoding no character’s code is the prefix of any other character’s code • To decode – Look for match left to right, bit by bit – Record letter when a match is found – Begin where you left off, going left to right 32

Information Representation Information representation in digital computers Program (code) – A sequence of instructions – Instruction contains opcode and operands Data – Text (alphanumeric codes): ASCII (7 b), Unicode (16 b) – Numbers • Integer: unsigned, sign-magnitude, 2’s complement • Floating point: sign-significand-exponent – 976, 000, 000 = 9. 76 * 1014 – 0. 000000976 = 9. 76 * 10 -14 – Multimedia • Image: 1024 x 768 pixels (1 b ~ 3 B per pixel) • Video, audio: MPEG

Machine Instruction MIPS Instruction: – add $8, $9, $10 Decimal number per field representation: 0 9 10 8 0 32 Binary number per field representation: 000000 01001 01010 01000 00000 100000 hex representation: decimal representation: Called a Machine Instruction 012 A 402016 19, 546, 14410 hex
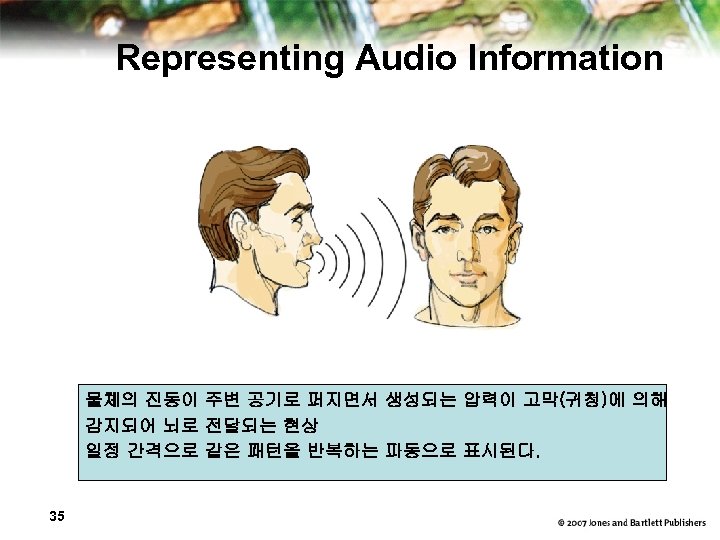
Representing Audio Information 물체의 진동이 주변 공기로 퍼지면서 생성되는 압력이 고막(귀청)에 의해 감지되어 뇌로 전달되는 현상 일정 간격으로 같은 패턴을 반복하는 파동으로 표시된다. 35
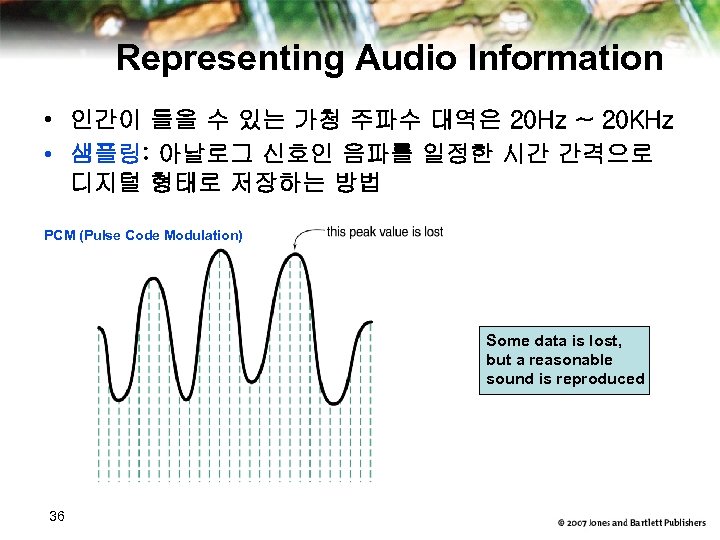
Representing Audio Information • 인간이 들을 수 있는 가청 주파수 대역은 20 Hz ~ 20 KHz • 샘플링: 아날로그 신호인 음파를 일정한 시간 간격으로 디지털 형태로 저장하는 방법 PCM (Pulse Code Modulation) Some data is lost, but a reasonable sound is reproduced 36

Digital Audio Formats – CD: 초당 44. 1 KHz로 2 채널 16비트로 샘플링된 오디오 – WAV: CD에 저장된 음원을 압축없이 저장한 형식 • 4분짜리 CD 오디오의 경우 2채널 * 2바이트 * 44. 1 K * 240 = 42 MB의 용량 필요 – FLAC: 무손실(lossless) 압축 형식 – MP 3: 손실(lossy) 압축 음원 형식 • MPEG-2, audio layer 3 파일 • Perceptual coding: 사람의 청각 특성을 이용하여 감도가 낮은 정 보를 생략하고 Huffman 코딩을 사용하여 비트 스트림을 추가 압 축 • CD에 비하여 75~95% (1/10) 크기로 압축 37

Representing Images • Digitizing an image – Representing a picture as a collection of individual dots called pixels – Pixel (picture element): a point in an image – Resolution: the number of pixels in an image – Each pixel can have a color • Color – Black or white: 1 bit – Grayscale: 8 bit – Color: expressed as an RGB(Red-Green-Blue) value • Each value indicates the relative contribution of each primary color 38

Representing Color • Color Depth – The amount of data that is used to represent a color • 8 bit color: 28 = 256 colors • High Color: 216 = 65536 colors – A 16 -bit color depth: 5 bits used for each number in an RGB value with the extra bit used to represent transparency • True Color: 224 = 16 M colors – A 24 -bit color depth: 8 bits used for each number in an RGB value 39

Representing Color Images 40

Digitized Images • Raster Graphics – Storage of data on a pixel-by-pixel basis – Bitmap format • Contains the pixel color value of the image from left to right and from top to bottom – Most images are stored in raster graphics format or compressed variations • Compressed Variations – GIF format • Each image is made up of only 256 colors • Use lossless compression for digital images – JPEG format • Use lossy compression for digital images • Achieve 10: 1 compression with little perceptible loss 41

Digitized Images and Graphics Whole picture Figure 3. 12 A digitized picture composed of many individual pixels 42

Digitized Images and Graphics Magnified portion of the picture See the pixels? Figure 3. 12 A digitized picture composed of many individual pixels 43

Vector Graphics – A format that describes an image in terms of lines and geometric shapes – A vector graphics image is a series of commands that describe a line’s direction, thickness, and color – The file sizes tend to be smaller because not every pixel is described – 장점: Vector graphics can be resized mathematically and changes can be calculated dynamically as needed – 단점: Vector graphics are not good for representing real-world images 44

Representing Video Vector codec (coder/decoder) – 비디오 파일은 엄청난 크기의 용량을 필요 • 1920 * 1080 픽셀의 해상도를 가지는 1시간 짜리 초당 30프레임의 비디오 파 일의 경우 1920 * 1080 * 3 (True Color) * 30 * 60 = 671 GB의 용량 필요 – 비디오를 컴퓨터에 저장하거나 네트워크에 전송하기 위해 파일의 크기를 줄이는 압축 표준 방식들 – 예: H. 264, MPEG 4, AVI, WMV – 대부분의 비디오 코덱은 파일의 크기를 줄이기 위하여 손실 (lossy) 압축을 사용 • Spatial compression: 한 frame에서 불필요한 정보를 제거 – 이미지 압축과 동일 • Temporal compression: frame 사이의 차이 정보만 전송 45

Homework 2 • Read Chapters 4 and 5 • Exercise – Chapter 2 • 1~5, 12~17, 21, 29, 34, 46 – Chapter 3 • 1~20, 28, 33, 40, 44, 48, 51, 53, 72 46
32394c8150aa45eb5a2de9f083fccdc9.ppt