ИНФОРМАТИКА Выигрышная стратегия 2014 г Кирсанов Илья Андреевич

ИНФОРМАТИКА Выигрышная стратегия. 2014 г. Кирсанов Илья Андреевич © C 3

ИНФОРМАТИКА Задача 1. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 22. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 22 или больше камней. В начальный момент в куче было S камней, 1 < S < 21. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. 2014 г. Кирсанов Илья Андреевич ©

ИНФОРМАТИКА Задача 1. Выполните следующие задания. Во всех случаях обосновывайте свой ответ. 1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S. б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани. 2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем - Петя не может выиграть за один ход, и - Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети. 3. Укажите значение S, при котором: - у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и - у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите Илья Андреевич © выигрышную стратегию Вани. 2014 г. Кирсанов

ИНФОРМАТИКА Задача 1. Чтобы ответить на данные вопросы, нам надо будет рассмотреть возможные варианты для переменной S. Для экономии времени, мы не станем рассматривать более 2 ходов для каждого из игроков. Для удобства представления информации, представим всю информацию в виде таблицы: 2014 г. Кирсанов Илья Андреевич ©

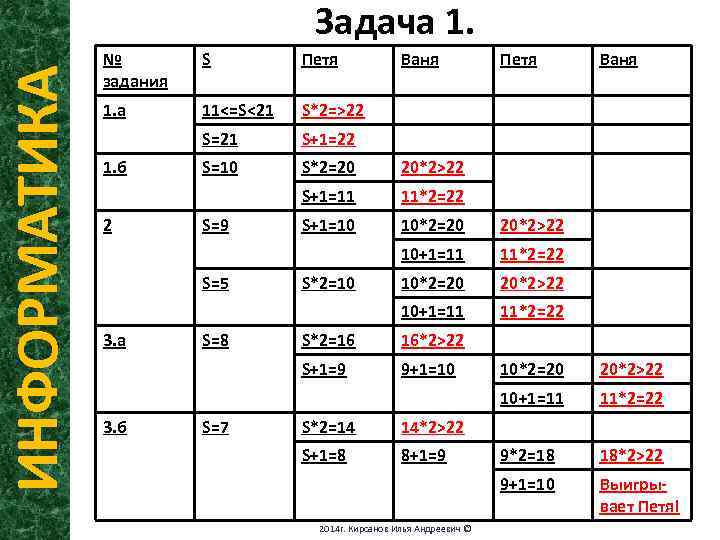ИНФОРМАТИКА Задача 1. № задания S Петя 1. а 11<=S<21 S*2=>22 S=21 S+1=22 S=10 S*2=20 20*2>22 S+1=11 11*2=22 S+1=10 10*2=20 20*2>22 10+1=11 11*2=22 1. б 2 S=9 S=5 3. а S=8 S*2=10 Ваня S*2=16 9+1=10 Ваня 16*2>22 S+1=9 Петя S=7 8+1=9 9*2=18 18*2>22 Выигрывает Петя! 14*2>22 S+1=8 11*2=22 9+1=10 S*2=14 20*2>22 10+1=11 3. б 10*2=20 2014 г. Кирсанов Илья Андреевич ©

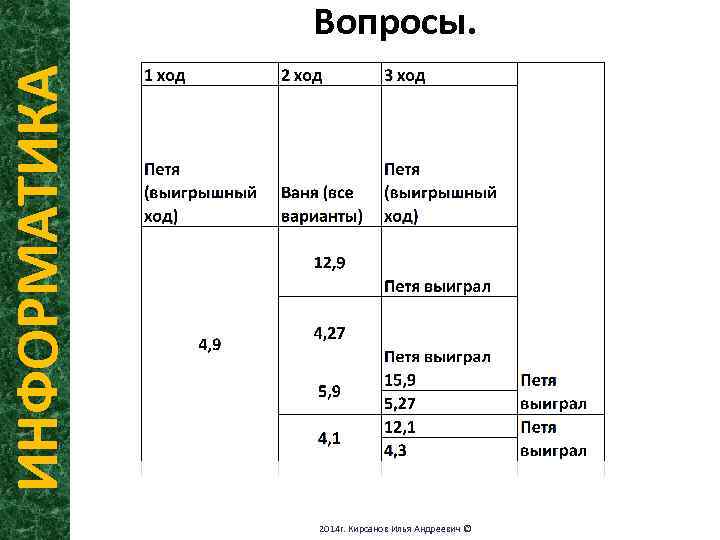
ИНФОРМАТИКА Вопросы. Два игрока, Петя и Ваня, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй - 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 20. Если в момент завершения игры общее число камней в двух кучах не менее 35, то выиграл Ваня, в противном случае - Петя. Кто выигрывает при безошибочной игре обоих игроков? Укажите, стратегию выигрывающего игрока - какой ход он должен сделать в каждой из позиций, которые могут ему встретиться при правильной игре. Докажите, что описанная стратегия - выигрышная. 2014 г. Кирсанов Илья Андреевич ©

ИНФОРМАТИКА Вопросы. 2014 г. Кирсанов Илья Андреевич ©