ИНФОРМАТИКА Лекция 6 Основы математической логики 1

ИНФОРМАТИКА Лекция № 6 Основы математической логики 1

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. 2

Понятие высказывания Высказывание - это повествовательное предложение, относительно которого можно определенно сказать, истинно оно или ложно. Например: "Луна - спутник Земли" - истинное высказывание, "Два больше трех" - ложное высказывание. "Как вы себя чувствуете? ", "Будь внимателен!" — не являются высказываниями и в алгебре высказываний не рассматриваются. Высказывания принято обозначать буквами латинского алфавита. Так, высказывание "Трава — зеленая" можно обозначить буквой А, "Лев -птица" - буквой В и т. д. 3

Значения истинности высказываний В алгебре высказываний отвлекаются от конкретного содержания высказывания и интересуются лишь вопросом, является ли оно истинным или ложным. . Каждому верному высказыванию присваивается значение истинности 1 (истинно), каждому неверному - значение истинности 0 (ложно). Например, А = 1, В = 0. 4

Операции над высказываниями Над высказываниями можно производить логические операции. В результате выполнения операций получаются новые высказывания, истинность которых определяется истинностью исходных высказываний и характером логических операций. 5

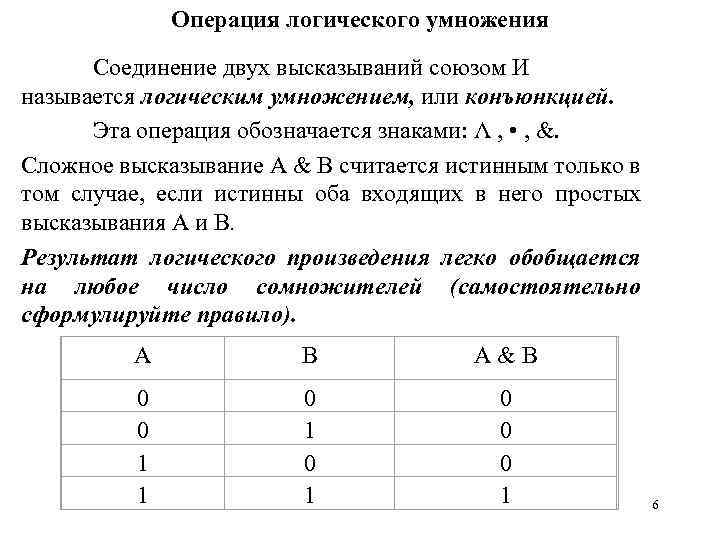Операция логического умножения Соединение двух высказываний союзом И называется логическим умножением, или конъюнкцией. Эта операция обозначается знаками: Λ , • , &. Сложное высказывание А & В считается истинным только в том случае, если истинны оба входящих в него простых высказывания А и В. Результат логического произведения легко обобщается на любое число сомножителей (самостоятельно сформулируйте правило). А В А & В 0 0 1 1 0 1 0 0 0 1 6

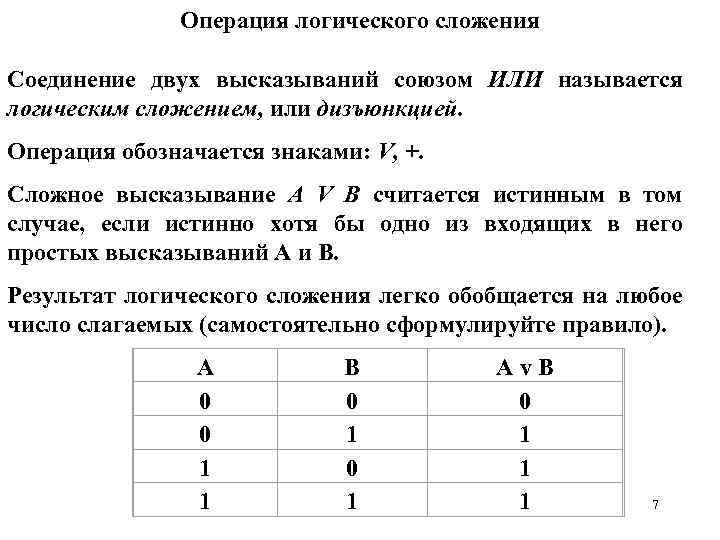Операция логического сложения Соединение двух высказываний союзом ИЛИ называется логическим сложением, или дизъюнкцией. Операция обозначается знаками: V, +. Сложное высказывание A V В считается истинным в том случае, если истинно хотя бы одно из входящих в него простых высказываний А и В. Результат логического сложения легко обобщается на любое число слагаемых (самостоятельно сформулируйте правило). А 0 0 1 1 В 0 1 А v В 0 1 1 1 7

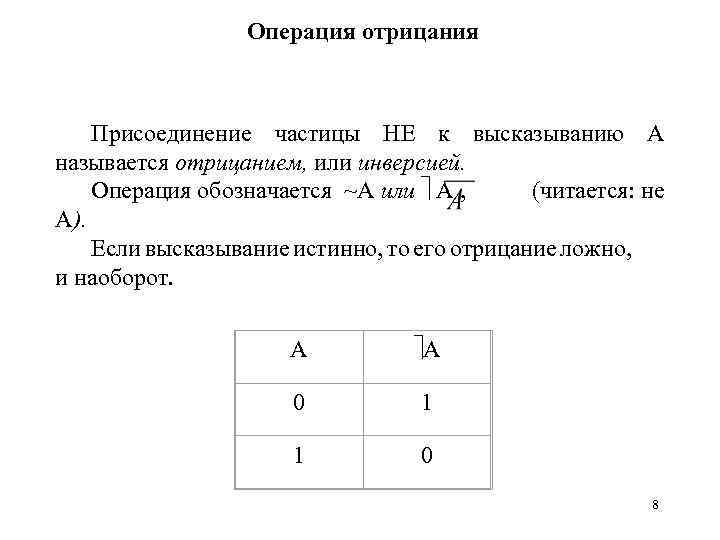Операция отрицания Присоединение частицы НЕ к высказыванию А называется отрицанием, или инверсией. Операция обозначается ~А или А , (читается: не А). Если высказывание истинно, то его отрицание ложно, и наоборот. А А 0 1 1 0 8

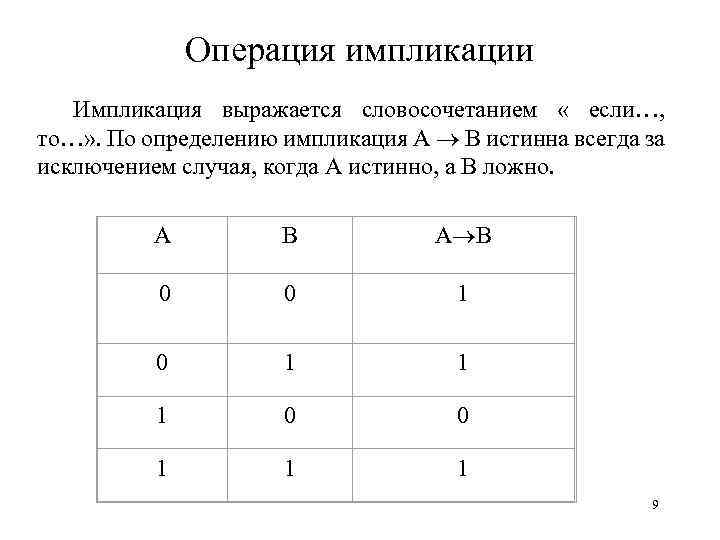Операция импликации Импликация выражается словосочетанием « если…, то…» . По определению импликация А В истинна всегда за исключением случая, когда А истинно, а В ложно. А В 0 0 1 1 1 9

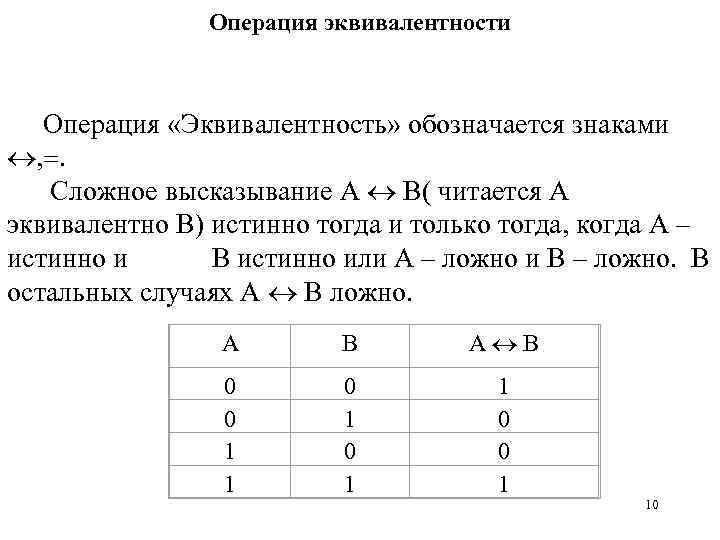Операция эквивалентности Операция «Эквивалентность» обозначается знаками , . Сложное высказывание А В( читается А эквивалентно В) истинно тогда и только тогда, когда А – истинно и В истинно или А – ложно и В – ложно. В остальных случаях А В ложно. А В А В 0 0 1 1 0 0 1 10

Операция штрих Шеффера A | B = (A&B) А В А | В 0 0 1 1 0 11

Операция стрелка Пирса A B = (AVB) А В 0 0 1 1 0 0 0 12

Операция «Сложение по модулю два» A B = A& B A& B А В А В 0 0 1 1 0 1 0 13

ЛОГИЧЕСКИЕ ФОРМУЛЫ 14

15

Порядок выполнения логических операций Отрицание - операция первой ступени. Конъюнкция (логическое умножение) операция второй ступени. Дизъюнкции (логического сложения) операция третьей ступени. Скобки используются для изменения порядка выполнения операций. 16

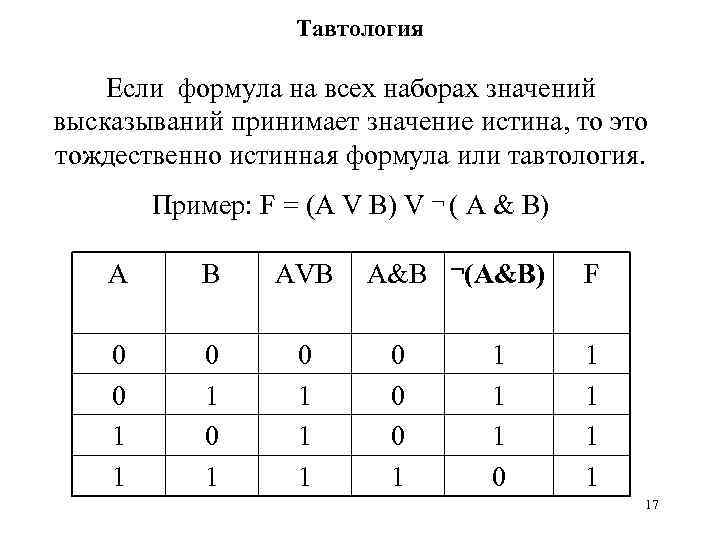Тавтология Если формула на всех наборах значений высказываний принимает значение истина, то это тождественно истинная формула или тавтология. Пример: F = (А V B) V ( A & B) A B AVB A&B (A&B) F 0 0 1 1 0 1 0 1 1 1 0 0 0 1 1 1 1 17

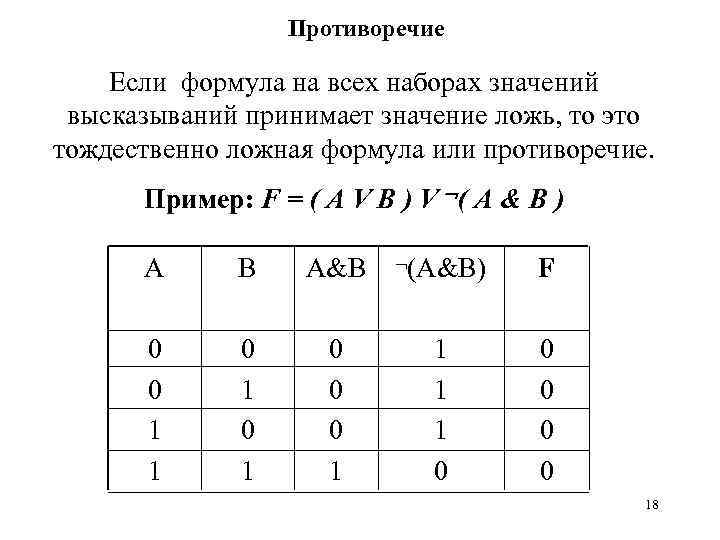Противоречие Если формула на всех наборах значений высказываний принимает значение ложь, то это тождественно ложная формула или противоречие. Пример: F = ( А V B ) V ( A & B ) A B A&B 0 0 1 1 0 1 0 0 0 1 (A&B) F 1 1 1 0 0 0 18

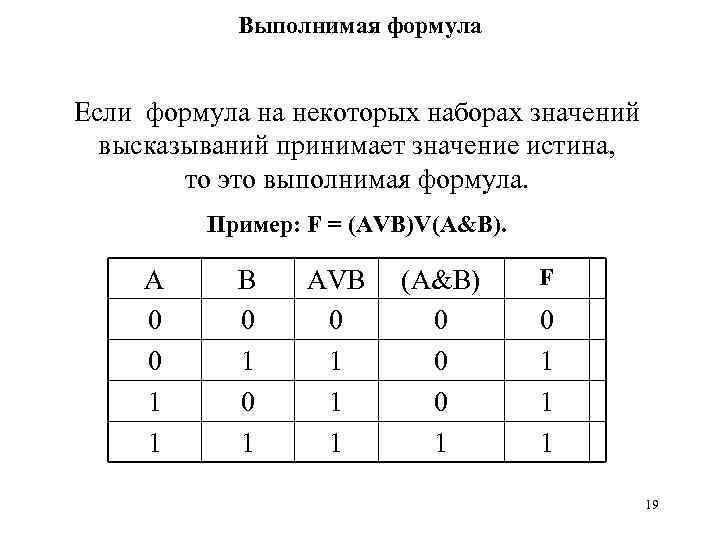Выполнимая формула Если формула на некоторых наборах значений высказываний принимает значение истина, то это выполнимая формула. Пример: F = (АVB)V(A&B). A 0 0 1 1 B 0 1 AVB 0 1 1 1 (A&B) 0 0 0 1 F 0 1 19

20

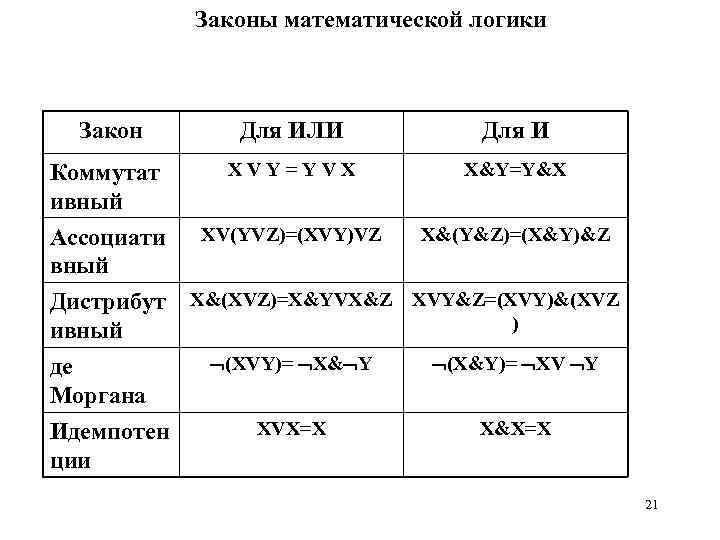Законы математической логики Закон Для ИЛИ Для И Коммутат ивный X V Y = Y V X X&Y=Y&X Ассоциати вный XV(YVZ)=(XVY)VZ X&(Y&Z)=(X&Y)&Z Дистрибут ивный де Моргана Идемпотен ции X&(XVZ)=X&YVX&Z XVY&Z=(XVY)&(XVZ ) (XVY)= X& Y (X&Y)= XV Y XVX=X X&X=X 21

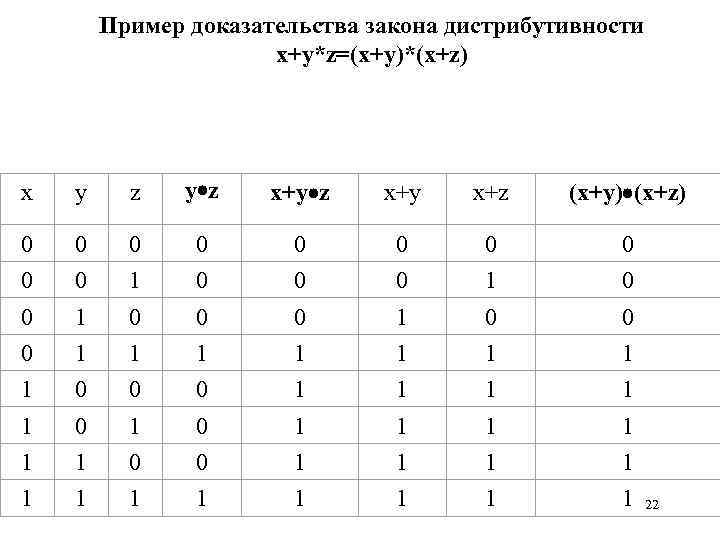Пример доказательства закона дистрибутивности x+y*z=(x+y)*(x+z) x 0 0 y 0 0 z 0 1 y z 0 0 x+y 0 0 x+z 0 1 (x+y) (x+z) 0 0 1 1 0 1 1 1 0 0 0 1 1 1 1 0 1 1 1 22

Законы математической логики • Формулы для отрицания: • Формулы для дизъюнкции: • Формулы для конъюнкции: • Правило действия со скобками: • Операция поглощения: • Операция склеивания: • Формулы де Моргана: 23

КАК УПРОСТИТЬ ЛОГИЧЕСКУЮ ФОРМУЛУ? Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики. 24

ПРИЕМЫ И СПОСОБЫ, ПРИМЕНЯЕМЫЕ ПРИ УПРОЩЕНИИ ЛОГИЧЕСКИХ ФОРМУЛ Законы алгебры логики применяются в следующей последовательности: 1. правило де Моргана; 2. сочетательный закон; 3. правило операций переменной с её инверсией; 4. правило операций с константами. 25

Примеры упрощения формул Пример 1. (применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией). Пример 2. (повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания). 26

Пример 3. (вводится вспомогательный логический сомножитель ( ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения); 27

Какая связь между алгеброй логики и двоичным кодированием? Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “ 1” и “ 0”. 28

Из этого следует два вывода: - одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных; - на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. 29

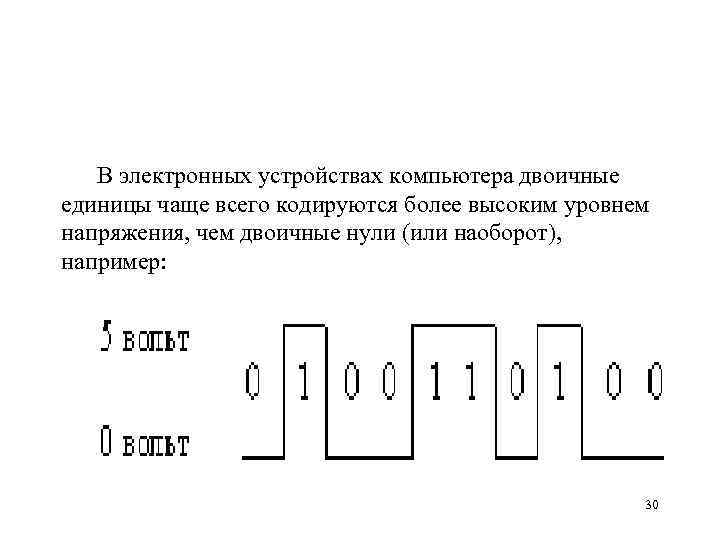В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например: 30

ЛОГИЧЕСКИЙ ЭЛЕМЕНТ КОМПЬЮТЕРА Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер. 31

ФУНКЦИИ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ Схема «И» реализует операцию логического умножения двух или более логических значений. Схема «ИЛИ» реализует логическое сложение двух или более логических значений. Схема «НЕ» реализует логическое отрицание логического значения. Схема «И-НЕ» реализует отрицание результата схемы «И» . Схема «ИЛИ-НЕ» реализует отрицание схемы «ИЛИ» . 32

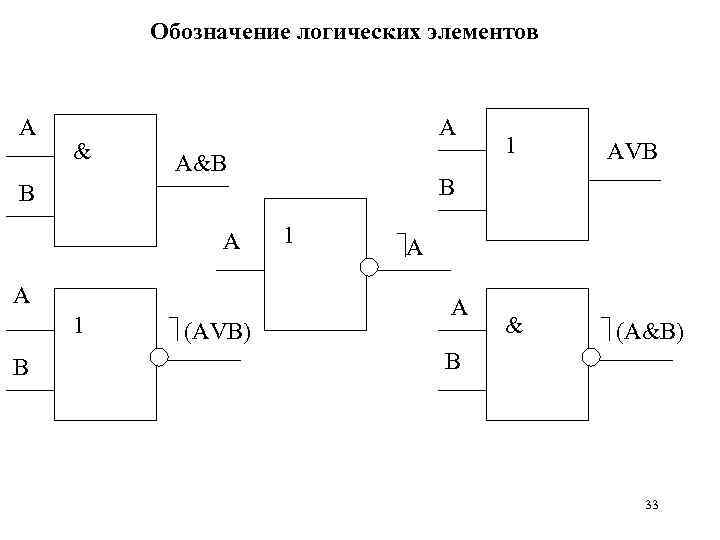Обозначение логических элементов A & A A&B A 1 B (AVB) AVB & (A&B) B B A 1 1 A A B 33

Построение электронной схемы по логическому выражению 1. Найдем группу операций одного типа выполняемых в последнюю очередь. Обозначим количество операций группы через k. 2. Выберем логический элемент. Соответствующий логическим операциям группы. 3. Свяжем с выходом логического элемента результат логического выражения. 4. Определим количество входов логического элемента. 5. Установим порядок выполнения логических операций. 6. Удалим из исходного логического выражения операции найденной группы. 7. Сопоставим каждому полученному выражению один из входов выбранного логического элемента. 34

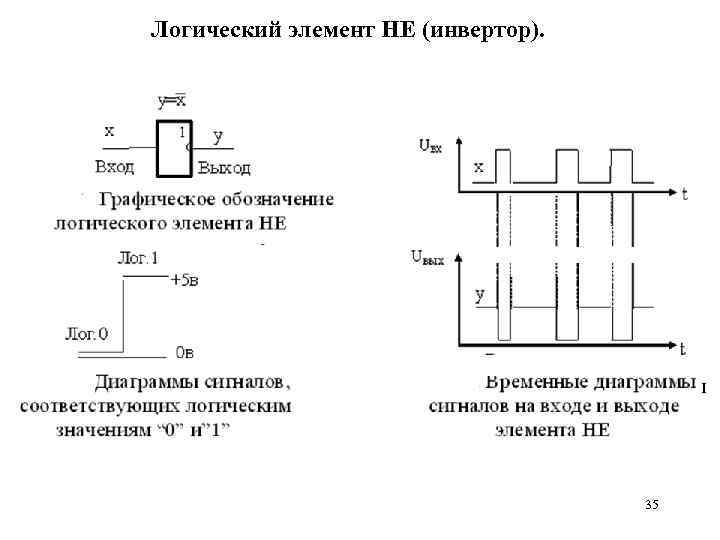Логический элемент НЕ (инвертор). 35

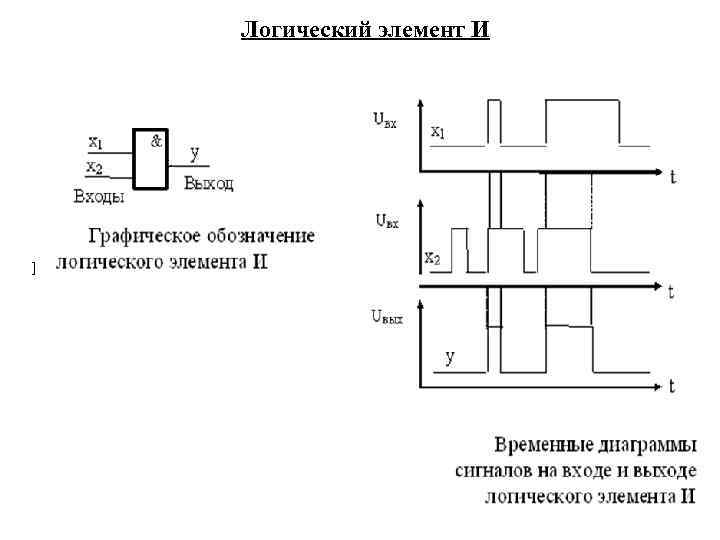Логический элемент И 36

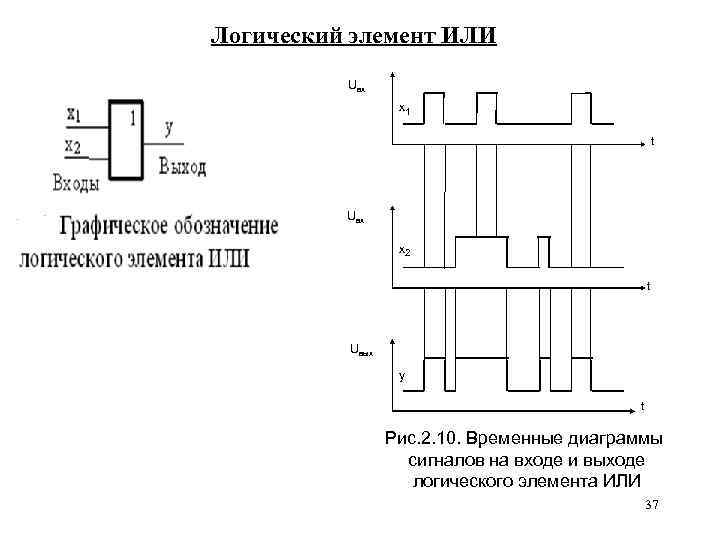Логический элемент ИЛИ Uвх х1 t Uвх х2 t Uвых у t Рис. 2. 10. Временные диаграммы сигналов на входе и выходе логического элемента ИЛИ 37

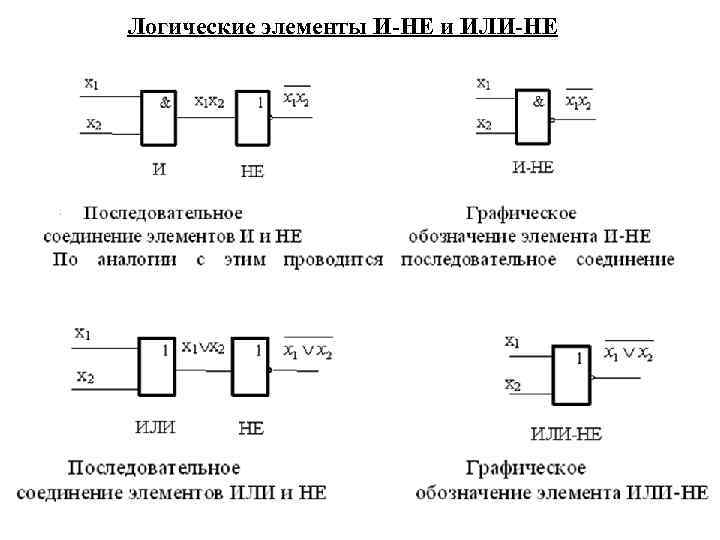Логические элементы И-НЕ и ИЛИ-НЕ 38

ПРИМЕР ПОСТРОЕНИЯ ЭЛЕКТРОННОЙ СХЕМЫ Исходное логическое выражение: E = D + B С + D (A + B), E = D + F+ G, Разбиение исходного выражения: D F = B С, G= D (A + B). 39

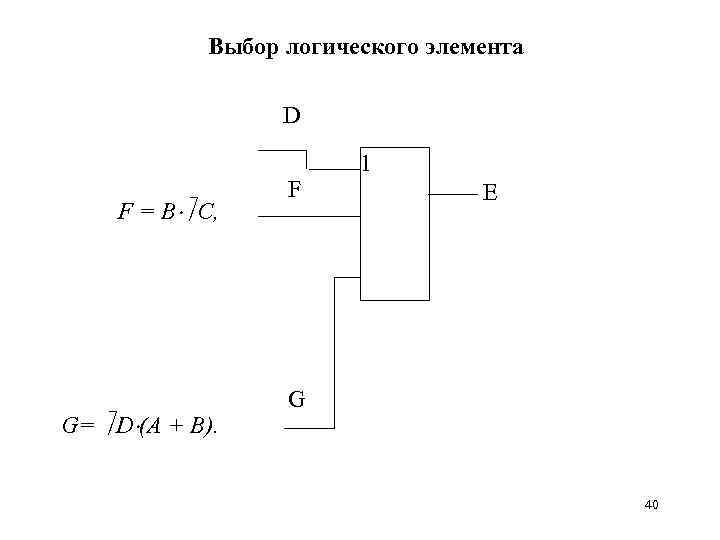Выбор логического элемента D F = B С, G= D (A + B). F 1 Е G 40

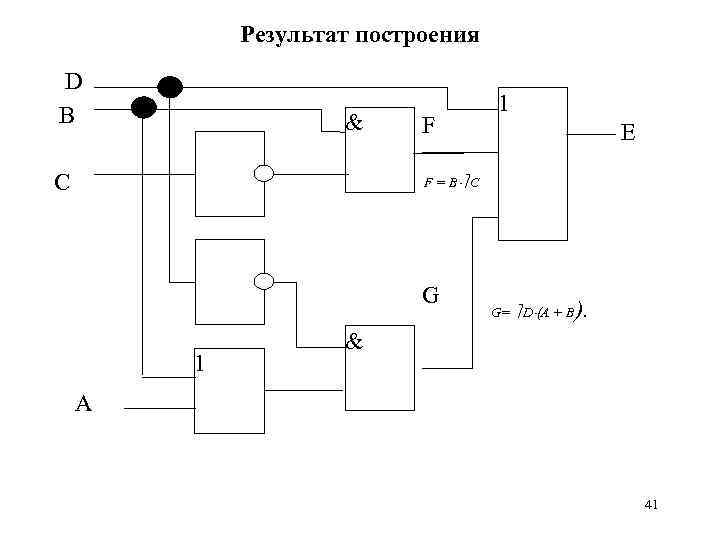Результат построения D В & C F 1 Е F = B С G 1 G= D (A + B ). & A 41

Триггеры – элементы памяти цифровых автоматов, в свою очередь являются элементарными цифровыми автоматами (автоматами Мура) с двумя устойчивыми состояниями. 42

Основные типы триггеров • триггер с раздельной установкой состояний (RS-триггер), • триггер "защелка" (D - триггер), • универсальный триггер (JK - триггер), • триггер со счетным входом (T - триггер) 43

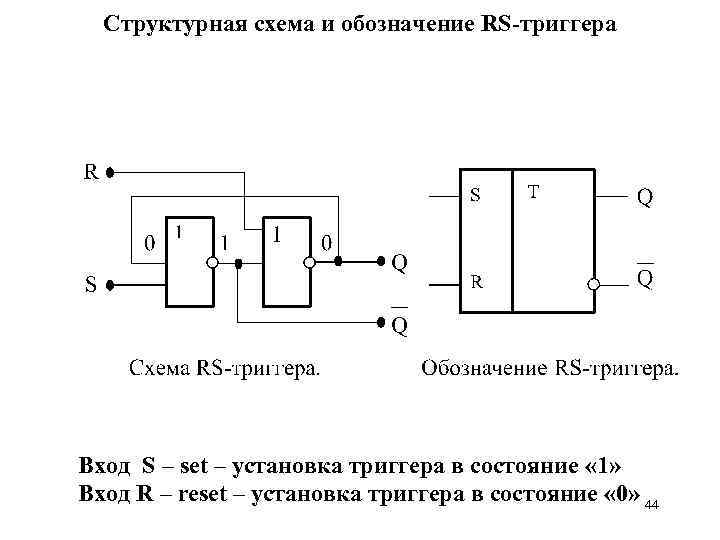Структурная схема и обозначение RS-триггера Вход S – set – установка триггера в состояние « 1» Вход R – reset – установка триггера в состояние « 0» 44

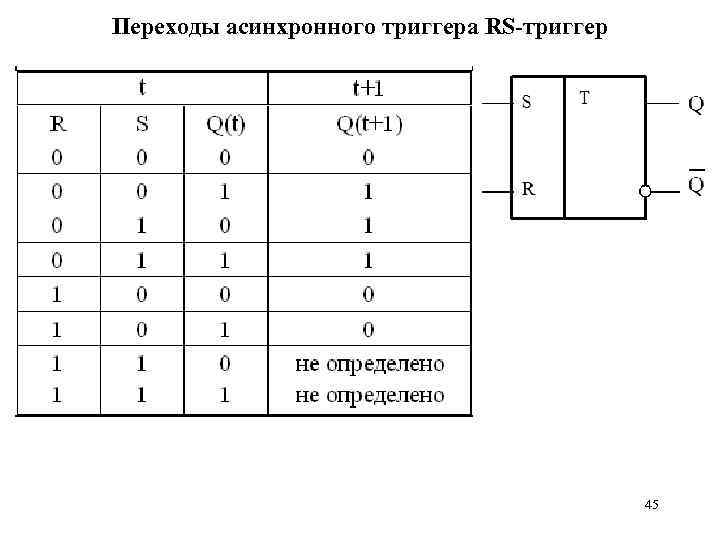Переходы асинхронного триггера RS-триггер 45

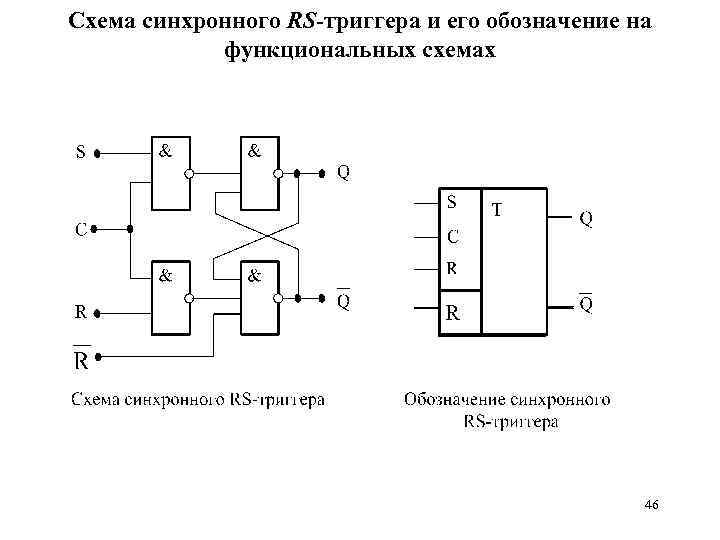Схема синхронного RS-триггера и его обозначение на функциональных схемах 46

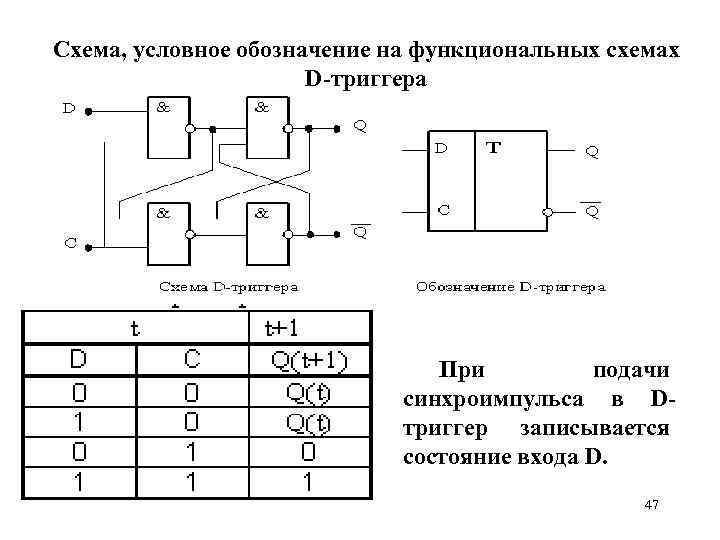Схема, условное обозначение на функциональных схемах D-триггера При подачи синхроимпульса в Dтриггер записывается состояние входа D. 47

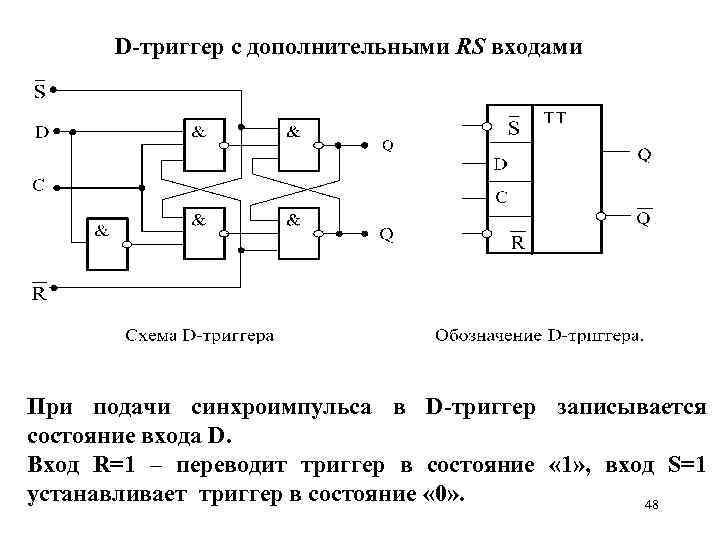D-триггер с дополнительными RS входами При подачи синхроимпульса в D-триггер записывается состояние входа D. Вход R=1 – переводит триггер в состояние « 1» , вход S=1 устанавливает триггер в состояние « 0» . 48

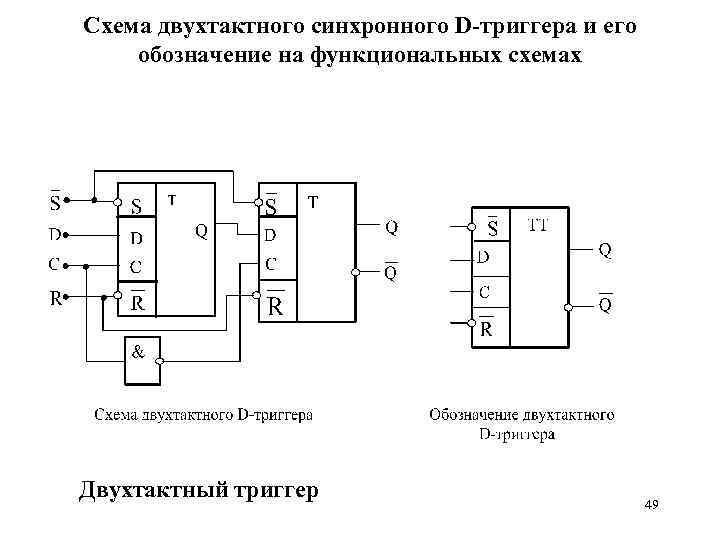Схема двухтактного синхронного D-триггера и его обозначение на функциональных схемах Двухтактный триггер 49

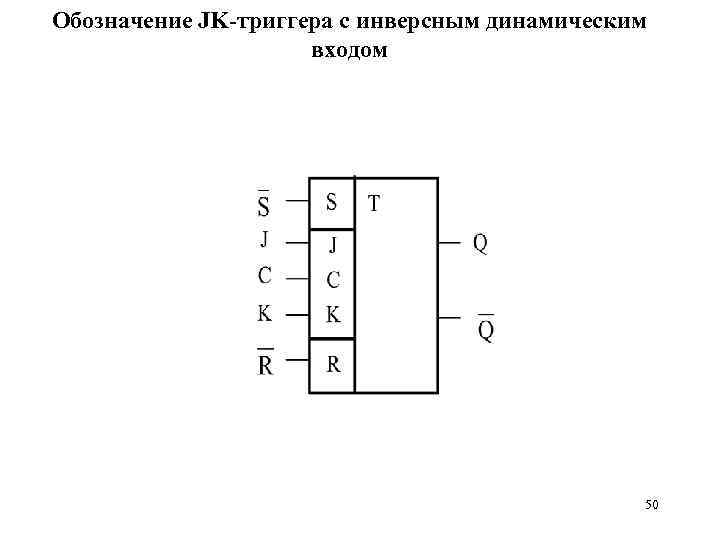Обозначение JK-триггера с инверсным динамическим входом 50

Вопросы по лекции 1. В чем отличие конечного автомата от комбинационных схем? 2. Как различаются автоматы Мура и Мили? 3. Сколько состояний имеет элементарный автомат? 4. Что такое триггер? 5. Почему Т-триггер называют триггером со счетным входом? 6. В какое состояние перейдет Т-триггер при входном сигнале Т = 1? 7. Какая запрещенная комбинация входных сигналов для RSтриггера? 8. В какое состояние перейдет RS-триггер при сигнале S = 1? 9. В какое состояние перейдет JK -триггер при сигнале К = 1? 10. В какое состояние перейдет JK -триггер при сигнале J = K = 1? 51

Вопросы по лекции 52

ЛЕКЦИЯ № Устройства ЦВМ 53

Дешифратор адреса предназначен для опознавания адреса устройства A. A 0 A 1 ДШ F A 2 A 3 A 2 A 1 A 0 (2) – запись адреса в двоичной системе счисления A 10 = A 3* 23 + A 2* 22 + A 1* 21 + A 0* 20 - адрес в десятичной системе счисления Если значение адреса A совпадает с значением адреса на входе устройства A, то на выходе дешифратора формируется сигнал 54 равный 1, в противном случае сигнал равный нулю.

Пример дешифратора Допустим, адрес устройства, которое подключается к адресной шине, равен 510 (0 l 0 l 2). По сигналу с дешифратора это устройство должно активизироваться, если на адресной шине появляется сигнал, равный пяти (Аз = 0, A 2. = 1, А 1 = 0, А 0 = 1), т. е. дешифратор распознает адресный код, равный пяти, и при этом на выходе дешифратора вырабатывается сигнал, равный логической единице. При любом другом значении адресного кода на выходе дешифратора вырабатывается сигнал, равный логическому нулю. Шина - это канал передачи электрических сигналов, который может состоять из нескольких параллельных проводников. Шина, предназначенная для передачи адреса устройства 55 называется шиной адреса.

Правило построения дешифратора адреса 1. Произведем перевод адресного кода из десятичной системы счисления в двоичную систему счисления и дополним полученное двоичное число слева нулями до необходимой разрядности n+1. 2. Сопоставим с каждым разрядом адресной шины высказывания: Аi, (i=0, . . . , n): Аn, …, А 2, А 1, А 0. 56

Правило построения дешифратора адреса 3. Запишем логическое выражение в виде логического произведения высказываний Bi (i = 0, . . . , n), количество которых совпадает с количеством разрядов адресной шины n+1. При этом каждый сомножитель Bi (i = 0, . . . , n) равен: Ai (i = 0, . . . , n), если соответствующий разряд двоичного числа равен 1; Аi (i = 0, . . . , n), если соответствующий разряд двоичного числа равен 0. 4. Применим алгоритм построения логических схем. 57

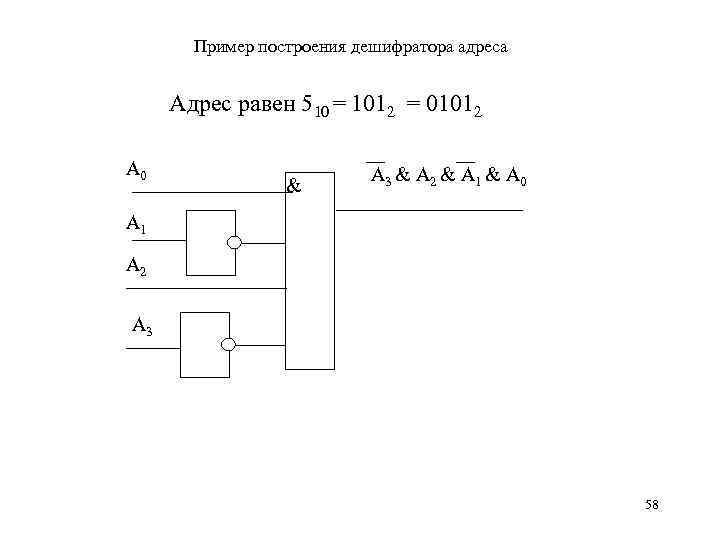Пример построения дешифратора адреса Адрес равен 510 = 1012 = 01012 А 0 & А 3 & А 2 & А 1 & А 0 А 1 А 2 А 3 58

Дешифратор кода операции Дешифраторы, преобразующие n-разрядное входное двоичное число (код) в единичный сигнал на одном из 2 n их выходов. Такие дешифраторы могут использоваться, например, для определения исполняемых машинных команд в устройстве управления ЭВМ. 59

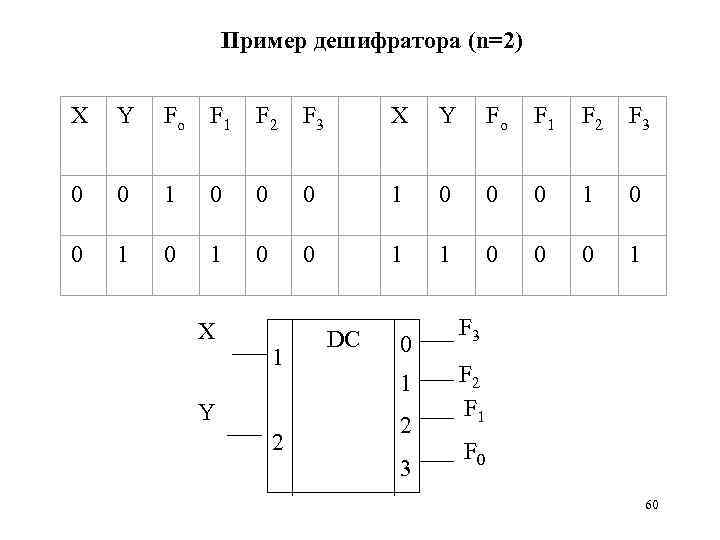Пример дешифратора (n=2) Х Y Fo F 1 F 2 F 3 X Y Fo F 1 F 2 F 3 0 0 1 0 1 0 0 1 1 0 0 0 1 X 1 Y 2 DC 0 1 2 3 F 2 F 1 F 0 60

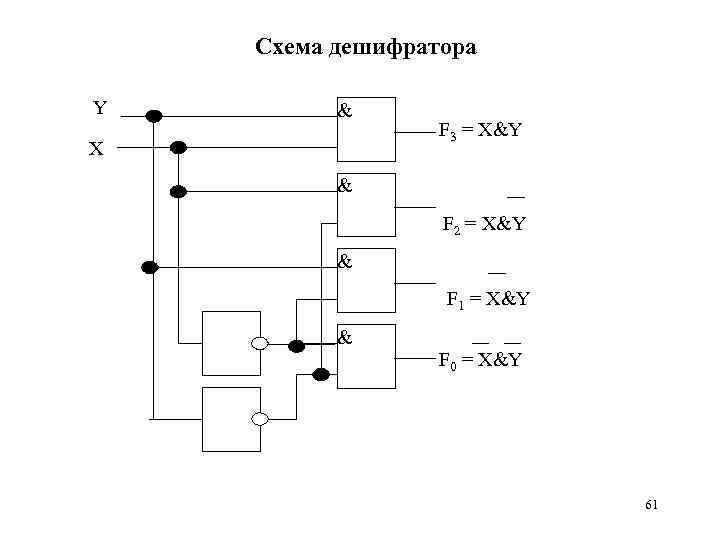Схема дешифратора Y & X F 3 = X&Y & F 2 = X&Y & F 1 = X&Y & F 0 = X&Y 61

Дешифратор кода операции Дешифратор – это устройство, которое имеет n входов и 2 n выходов, причем каждой i-ой комбинации сигналов на входе соответствует сигнал на одном определенном 2 i-ом выходе. Другими словами, дешифратор – это устройство, которое дешифрирует число в позицию. Дешифраторы предназначены для декодирования (распознавания) кодовых комбинаций (адрес устройства, код операции и т. д. ). 62

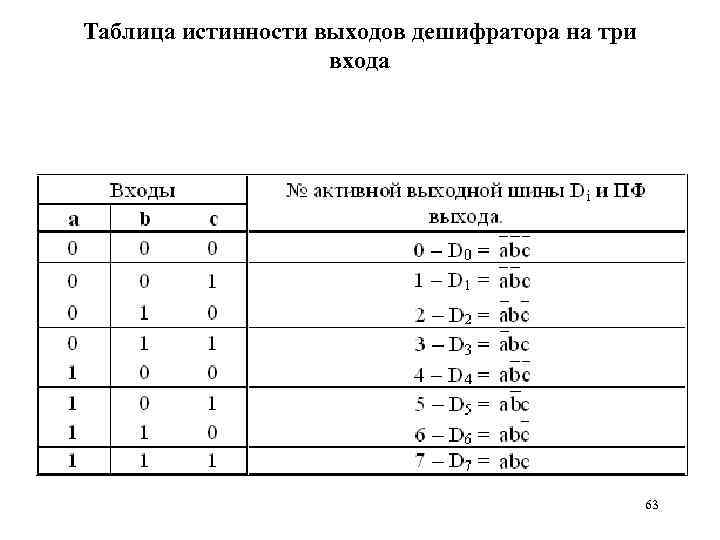Таблица истинности выходов дешифратора на три входа 63

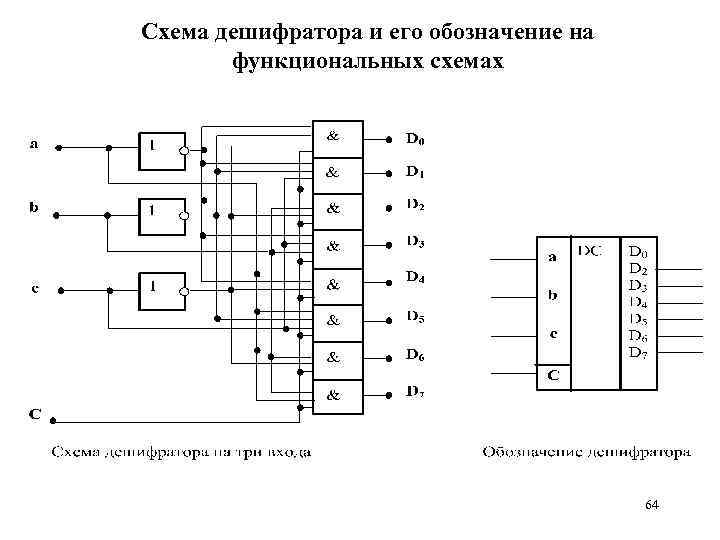Схема дешифратора и его обозначение на функциональных схемах 64

Полусумматор осуществляет сложение одноразрядных чисел по следующим правилам: двоичных 0+0=00; 0; +1=01; 1+0=01; 1+1=10. Полусумматор имеет два входа: А -. первое слагаемое, В - второе слагаемое, и два выхода: S — значение суммы в данном разряде, Р - значение переноса в старший разряд. В этом устройстве отсутствует третий вход для переноса единицы из младшего разряда. 65

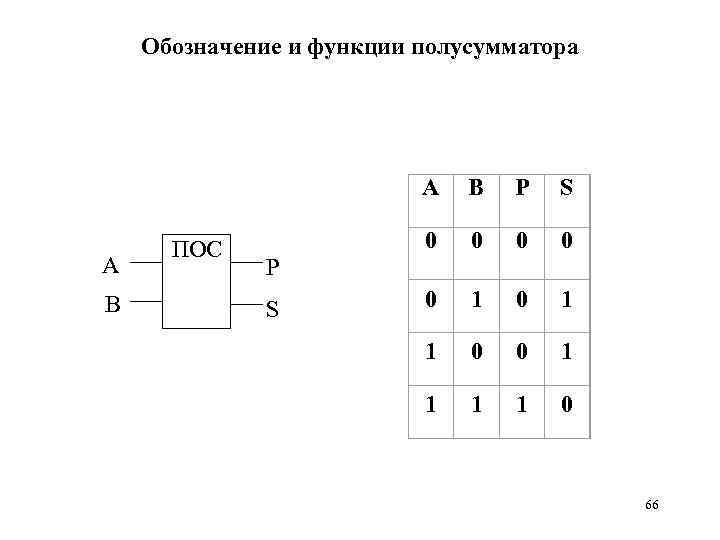Обозначение и функции полусумматора А А В ПОС В P S 0 0 0 1 1 0 P S 66

Построение полусумматора А В P S 0 0 0 1 1 0 Логические выражения, определяющие состояние выходов S и Р, имеют следующий вид: S=A • B+ A • B (*), Р = А • В. Преобразуем логическое выражение для выхода S, сложим выражение (*) с тождественно ложным высказыванием А • А + В • В: S = A • B+ A • B + А • А + В • В : 67

Воспользуемся коммуникативными и дистрибутивными свойствами : S = ( А + В) • (А+В). С учетом закона де Моргана имеем: S = (А • В) • (А+В). 68

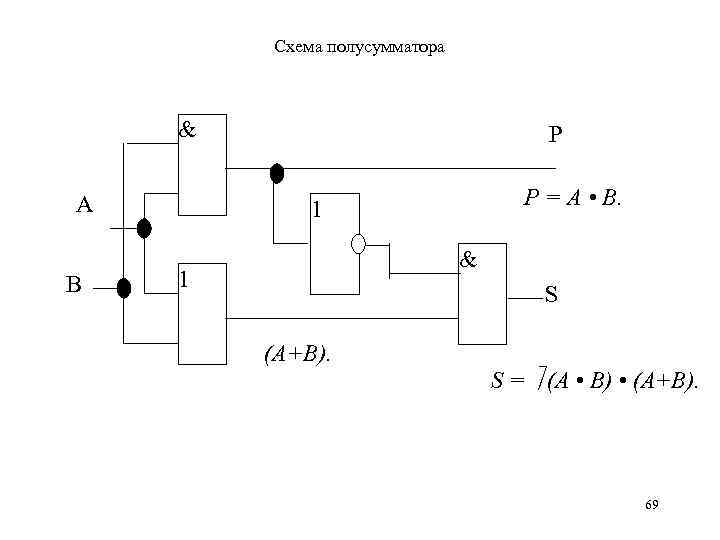Схема полусумматора & А В Р Р = А • В. 1 & 1 S (А+В). S = (А • В) • (А+В). 69

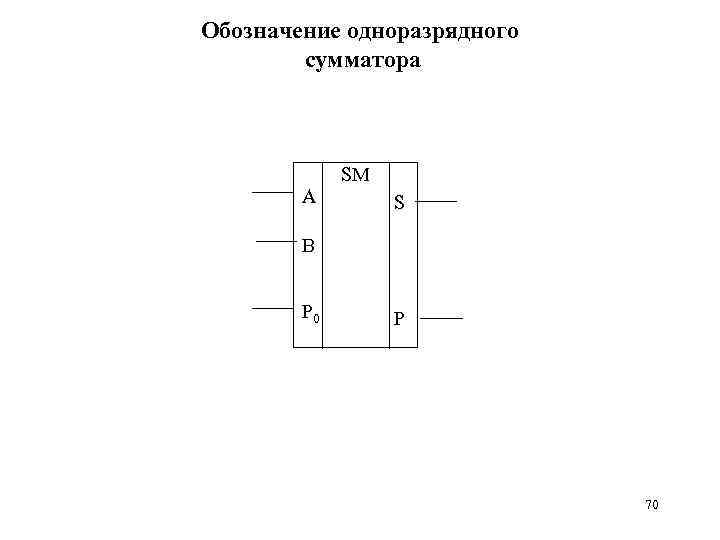Обозначение одноразрядного сумматора A SM S В P 0 P 70

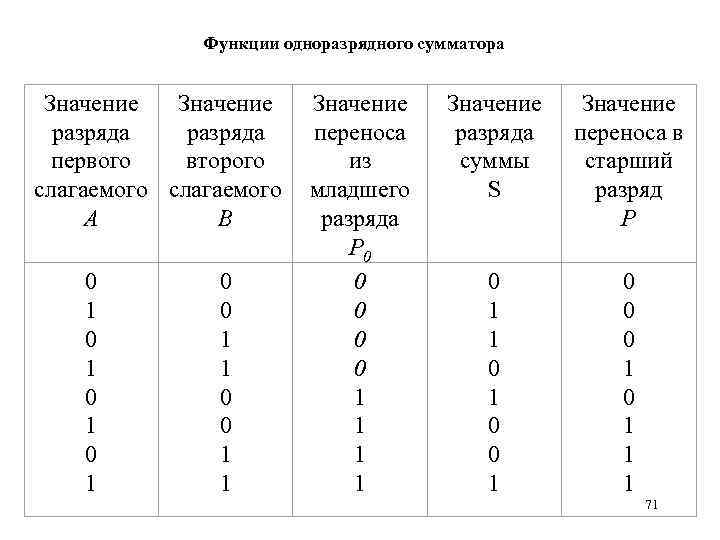Функции одноразрядного сумматора Значение разряда первого второго слагаемого А В 0 1 0 1 0 0 1 1 Значение переноса из младшего разряда P 0 0 0 1 1 Значение разряда суммы S Значение переноса в старший разряд Р 0 1 1 0 0 0 1 1 1 71

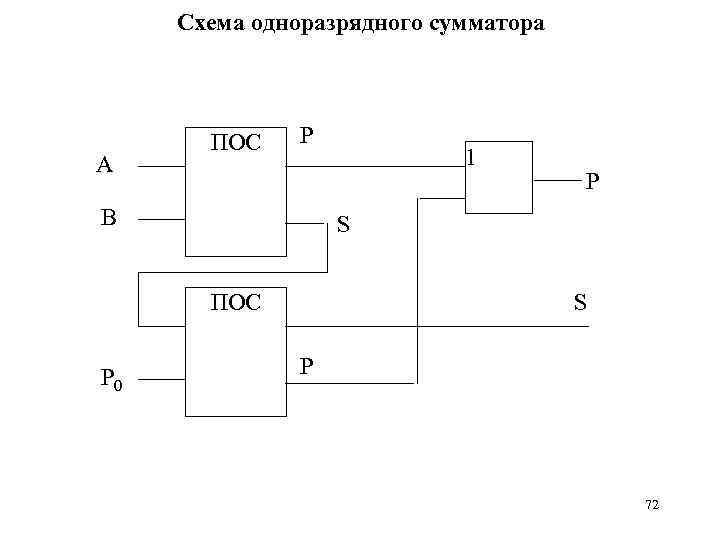Схема одноразрядного сумматора А ПОС P В Р S ПОС Р 0 1 S P 72

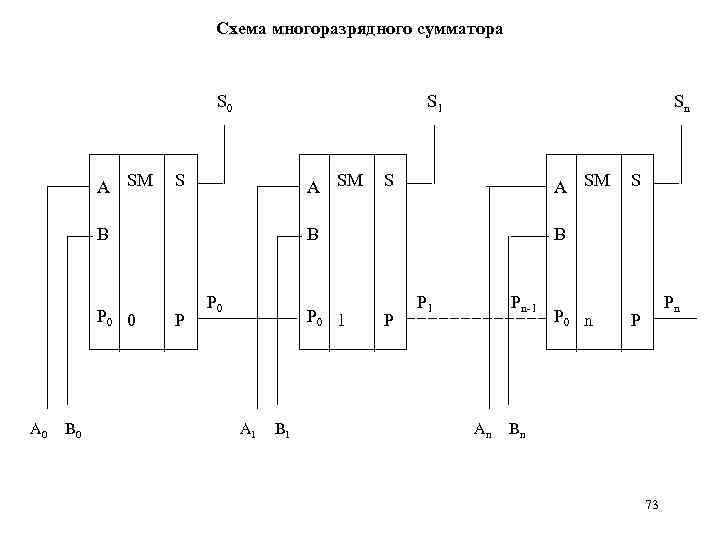Схема многоразрядного сумматора S 0 А SM S 1 S А SM В Р 0 0 А 0 В 0 Sn S А SM В P Р 0 1 А 1 В 1 S В P Р 1 Рn-1 Аn Р 0 n Рn P Вn 73

Регистры — это набор простейших запоминающих устройств (например, триггеров) для временного хранения двоичной информации в устройствах обработки информации. - Основные виды регистров: Параллельные - Последовательные 74

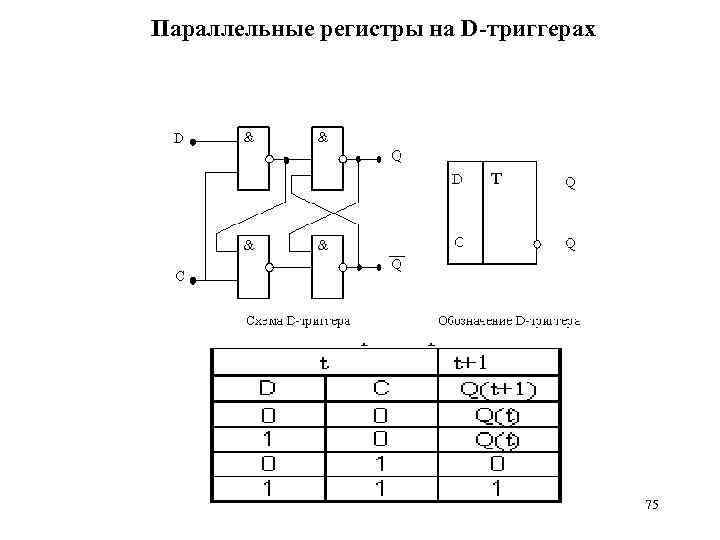Параллельные регистры на D-триггерах 75

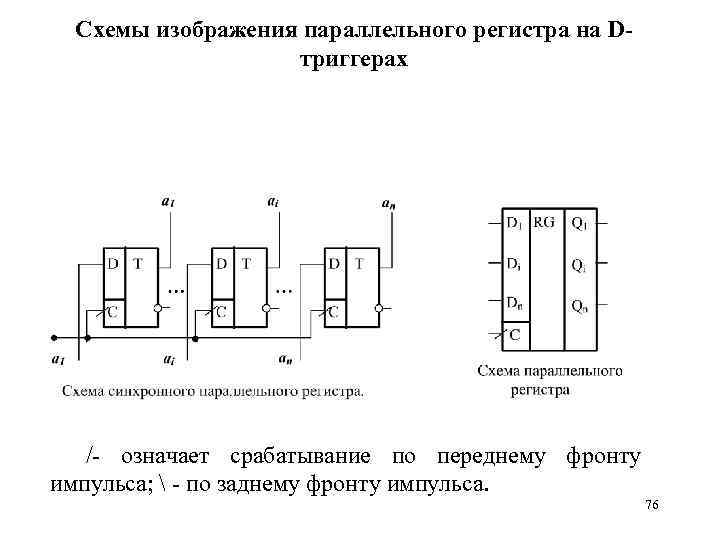Схемы изображения параллельного регистра на Dтриггерах /- означает срабатывание по переднему фронту импульса; - по заднему фронту импульса. 76

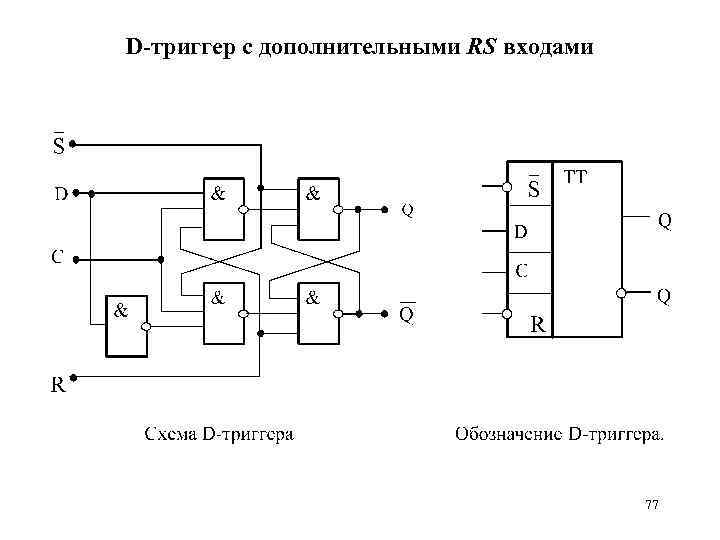D-триггер с дополнительными RS входами 77

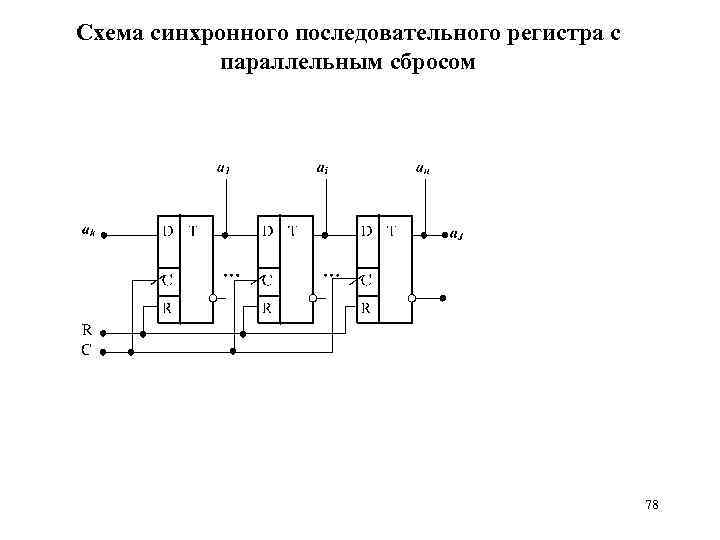Схема синхронного последовательного регистра с параллельным сбросом 78

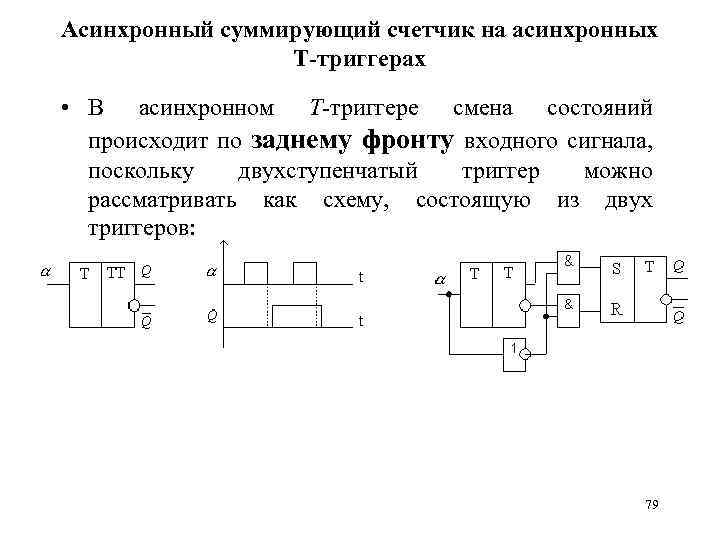Асинхронный суммирующий счетчик на асинхронных Т-триггерах • В асинхронном Т-триггере смена состояний происходит по заднему фронту входного сигнала, поскольку двухступенчатый триггер можно рассматривать как схему, состоящую из двух триггеров: 79

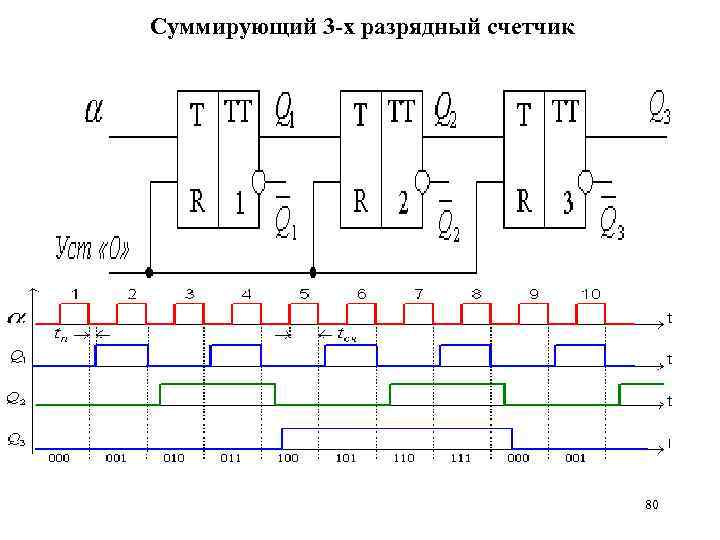Суммирующий 3 -х разрядный счетчик 80

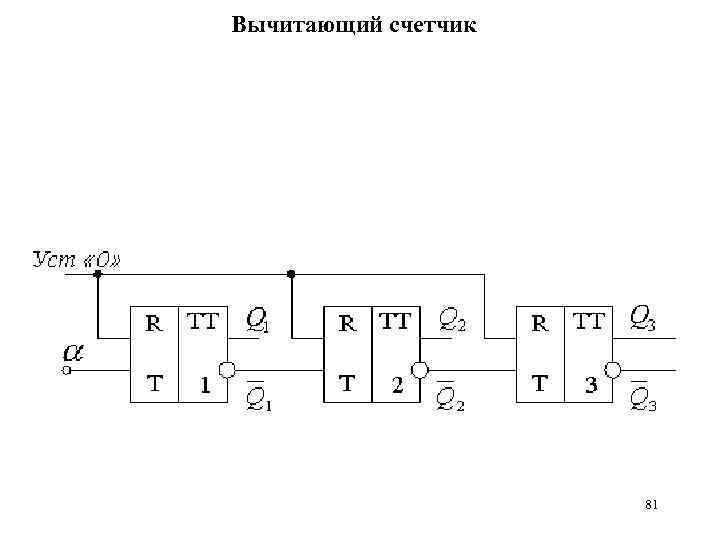Вычитающий счетчик 81

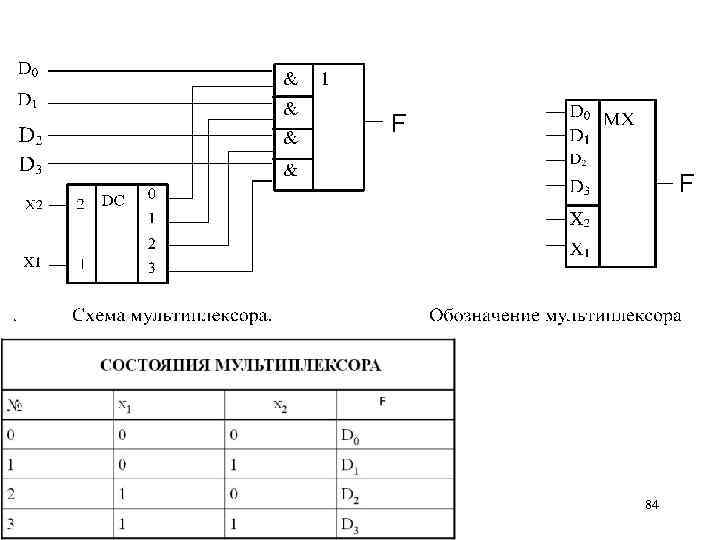
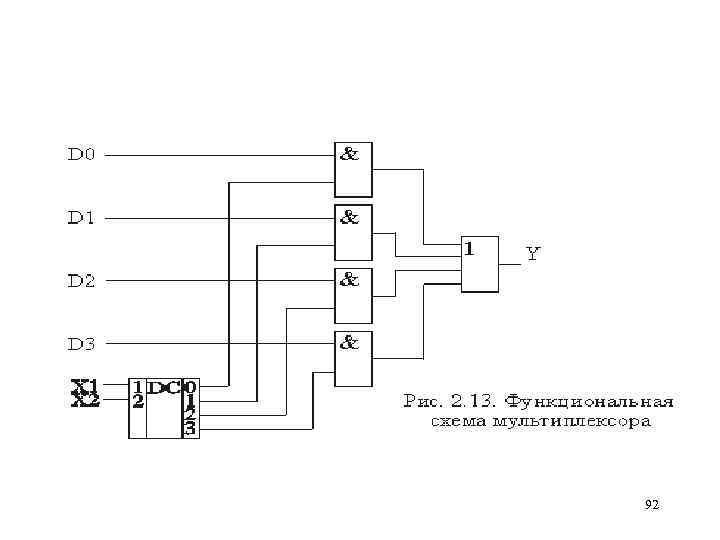
Мультиплексор (MX, MUL), –это электронное устройство, которое имеет несколько информационных D -входов и один выход F, осуществляющее последовательное подключение входов к выходу в соответствии с адресным кодом, поступающим на управляющие (адресные) входы (х1, х2). 82

Mультиплексор Mультиплексор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов. Аналоговые и цифровые мультиплексоры значительно различаются по принципу работы. Первые электрически соединяют выбранный вход с выходом (при этом сопротивление между ними невелико — порядка единиц/десятков ом). Вторые же не образуют прямого электрического соединения между выбранным входом и выходом, а лишь «копируют» на выход логический уровень ('0' или '1') с выбранного входа. Аналоговые мультиплексоры иногда называют ключами. Устройство, противоположное мультиплексору по своей функции, называется демультиплексором. 83

84

Демультиплексор – это устройство, имеющее один информационный вход D и несколько выходов, осуществляющее передачу сигнала с информационного входа на один из выходов в соответствии с управляющим (адресным) кодом, поступающим на управляющие входы. В простейшем случае, в качестве демультиплексора может использоваться дешифратор, у которого вместо сигнала OE подается информационный сигнал X. Например, если на входы подать код a 1 a 0=10(2)=2(10), то сигнал X появится на выходе y 2, а на остальных выходах yi=0. 85

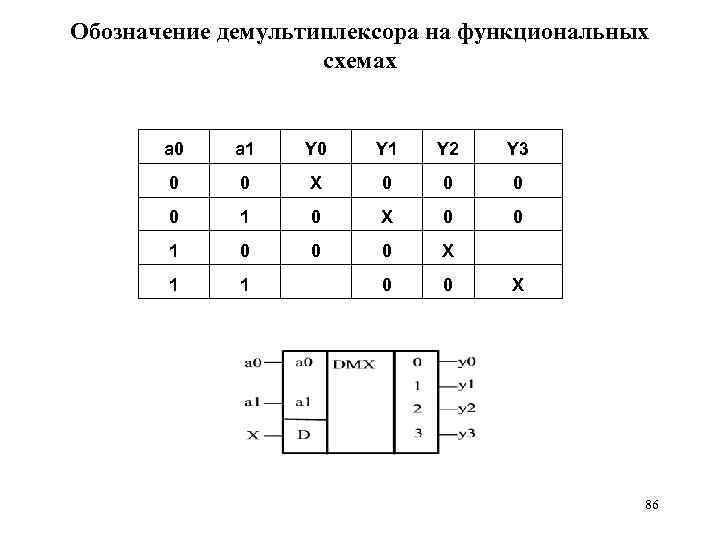Обозначение демультиплексора на функциональных схемах a 0 a 1 Y 0 Y 1 Y 2 Y 3 0 0 X 0 0 1 0 0 0 X 1 1 0 0 X 86

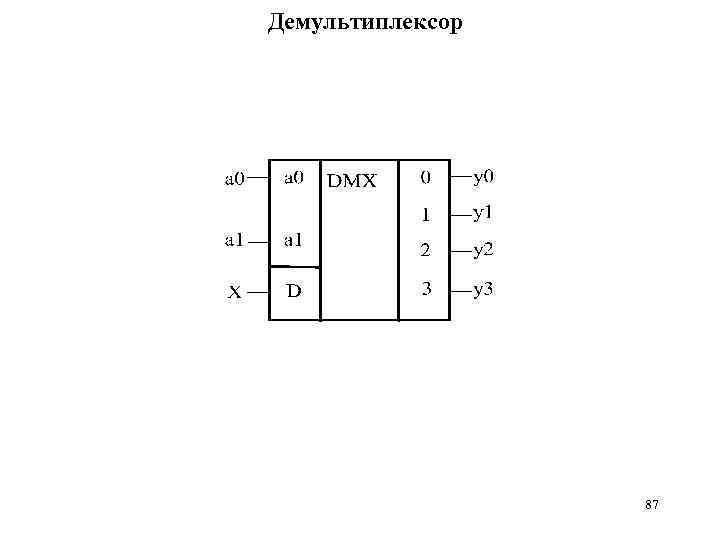Демультиплексор 87

Конец 88

Мультиплексор Mультиплексор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передавать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов. Устройство, противоположное мультиплексору по своей функции, называется демультиплексором. 89

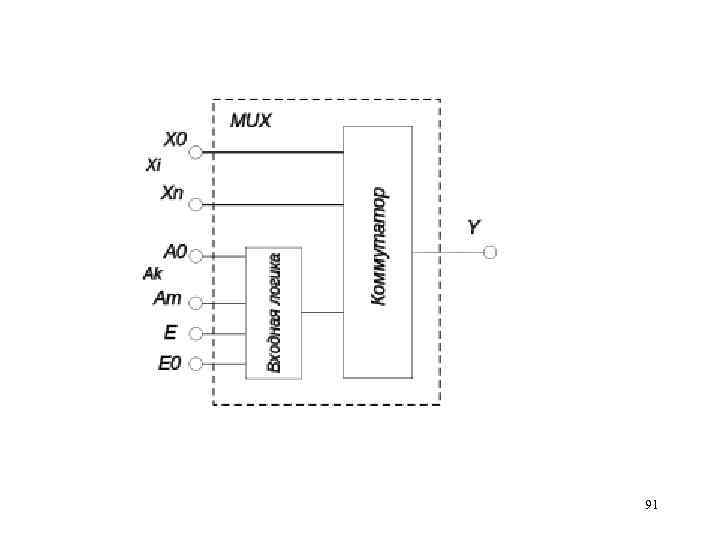
Мультиплексор - коммутатор цифровых сигналов. Мультиплексор представляет собой комбинационное устройство с m информационными, n управляющими входами и одним выходом. Функционально мультиплексор состоит из m элементов конъюнкции, выходы которых объединены дизъюнктивно с помощью элемента ИЛИ с m входами. На одни входы всех элементов конъюнкции подаются информационные сигналы, а другие входы этих элементов соединены с соответствующими выходами дешифратора с n 90

91

92

Схемное обозначение мультиплексора 4>1 93

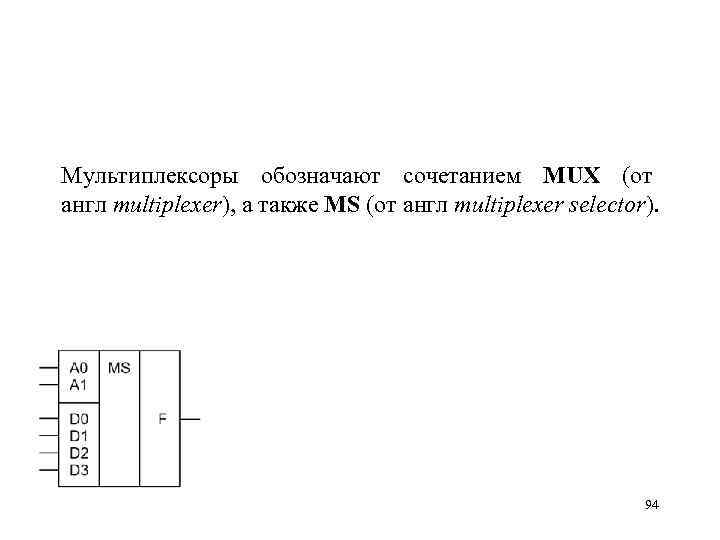Мультиплексоры обозначают сочетанием MUX (от англ multiplexer), а также MS (от англ multiplexer selector). 94

Использование мультиплексоров Мультиплексоры могут использоваться в делителях частоты, сдвигающих устройствах и др. Мультиплексоры часто используют для преобразования параллельного двоичного кода в последовательный. Для такого преобразования достаточно подать на информационные входы мультиплексора параллельный двоичный код, а сигналы на адресные входы подавать в такой последовательности, чтобы к выходу поочередно подключались входы, начиная с первого и заканчивая последним. 95