ИНФОРМАТИКА Кафедра Информационные системы Представление информации в

ИНФОРМАТИКА Кафедра «Информационные системы»

Представление информации в ЭВМ Лекция 1

Понятие информации Информационный процесс – последовательность действий, выполняемых с информацией; n

Понятие информации Информационная система – система, реализующая информационные процессы; n

Понятие информации Сообщение – форма представления информации в виде совокупности знаков (символов), используемая для передачи.

Понятие информации Сообщение рассматривается на 3 х уровнях: n n n синтаксический; семантический; прагматический.

Функции информации n Познавательная – получение новой информации;

Функции информации n n Познавательная – получение новой информации; Коммуникативная – функция общения людей;

Функции информации n n n Познавательная – получение новой информации; Коммуникативная – функция общения людей; Управленческая – формирование целесообразного поведения управляемой системы.

Меры информации Для измерения водятся два параметра: 1. Объем информации – Vg (объемный подход)

Меры информации Для измерения водятся два параметра: 1. Объем информации – Vg (объемный подход) 2. Количество информации – I (энтропийный подход)

Объемный подход Объем информации Vg – равен количеству символов (разрядов) в сообщении. n

10 -ная система счисления 1 разряд имеет вес 10, единица измерения – ДИТ (десятичный разряд)

10 -ная система счисления 1 разряд имеет вес 10, Берем N-разрядное число Vg = N дит

10 -ная система счисления Пример: 2006 Vg = ?

2 -ная система счисления 1 разряд имеет вес 2, единица измерения – БИТ (двоичный разряд)

2 -ная система счисления Берем N-разрядное число Vg = N бит

2 -ная система счисления Пример: 11001011 Vg = ?

Измерение двоичной информации 1 Байт = 8 Бит;

Измерение двоичной информации 1 Байт = 8 Бит; 1 Кбайт=1024 Кбайт=210 байт;

Измерение двоичной информации 1 Байт = 8 Бит; 1 Кбайт=1024 Кбайт=210 байт; 1 Мбайт=1024 Кбайт=220 байт;

Измерение двоичной информации 1 Байт = 8 Бит; 1 Кбайт=1024 Кбайт=210 байт; 1 Мбайт=1024 Кбайт=220 байт; 1 Гбайт=1024 Мбайт=230 байт;

Измерение двоичной информации 1 Байт = 8 Бит; 1 Кбайт=1024 Кбайт=210 байт; 1 Мбайт=1024 Кбайт=220 байт; 1 Гбайт=1024 Мбайт=230 байт; 1 Тбайт=1024 Гбайт=240 байт.

Энтропийный подход Количество информации I – мера уменьшения неопределенности (энтропии) состояния данной системы после получения сообщения.

Энтропийный подход Количество информации I – мера уменьшения неопределенности (энтропии) состояния данной системы после получения сообщения. I = Hapr – Haps

Принципы построения ПК n Программное управление В основе лежит представление алгоритма решения любой задачи в виде программы вычислений.

Принцип двоичного кодирования Вся информация кодируется 0 или 1 Каждый тип информации имеет свой формат.

Принцип двоичного кодирования Последовательность битов в формате, имеющая определенный смысл, называется полем.

Принцип адресности Основная память состоит из пронумерованных ячеек. В произвольный момент времени процессору доступна любая ячейка.

Принцип адресности Двоичные коды команд разделяются на слова и хранятся в ячейках памяти, для доступа к ним используются адреса – номера соответствующих ячеек.

Принцип программного управления Все вычисления, предусмотренные алгоритмом, должны быть представлены в виде программы, состоящей из последовательности управляющих слов - команд.

Принцип программного управления Команды программы хранятся в ячейках памяти ПК и выполняются в естественной последовательности.

Принцип однородности памяти Команды и данные хранятся в одной и той же памяти и внешне в памяти неразличимы.

Принцип однородности памяти Команды одной программы могут быть получены как результат выполнения другой программы – основа трансляции.

Группы характеристик структуры ПК n Технические характеристики;

Группы характеристик структуры ПК n n Технические характеристики; Характеристики функциональных модулей базовой конфигурации;

Группы характеристик структуры ПК n n n Технические характеристики; Характеристики функциональных модулей базовой конфигурации; Состав ПО и сервисных услуг.

Основные характеристики Быстродействие – число определенного типа команд, выполняемых ПК за 1 секунду.

Быстродействие Общая характеристика – тактовая частота микропроцессора. n Важны тип микропроцессора и его структурные особенности.

Основные характеристики Производительность – объем работ(число программ), выполняемых ПК в единицу времени.

Как измерить? 1. MIPS (Million Instructions Per Second);

Как измерить? 1. MIPS (Million Instructions Per Second); 2. МFLOPS (Million Floating Point Operations Per Second);

Емкость запоминающих устройств Емкость памяти измеряется количеством структурных единиц информации, которое может одновременно находится в памяти.

Емкость памяти Размер ячейки памяти– один байт. 1 Байт = 8 Бит; n Для хранения больших чисел используют 2, 4 или 8 байт, размещаемых в ячейках с последовательными адресами.

Емкость памяти Пример: 32 -х разрядное число Хранится в ячейках с адресами 200, 201, 202, и 203

Надежность - способность ПК при определенных условиях выполнять требуемые функции в течение заданного периода времени;

Точность - возможность ПК различать почти равные значения.

Точность результатов определяется: 1. Разрядностью ПК 2. Структурными единицами представления информации (байт, слово, двойное слово).

Точность в применении Обработка текстов – 8 ми и 16 ти разрядные двоичные коды. n Математические расчеты – Используют двоичные коды с высокой разрядностью(32, 64 и более) n

Достоверность - свойство информации быть правильно воспринятой.

Достоверность Главная характеристика - вероятность получения безошибочных результатов. Обеспечивается аппаратно-программными средствами ПК.

Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр).

Непозиционная система счисления Система, в которой символы, обозначающие то или иное количество, не меняют своего значения в зависимости от местоположения(позиции) в изображении числа. AD = D 1+D 2+…+DN В непозиционных системах вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа!

Примеры 1. В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. 2. 3252 – это три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы). Величина числа не зависела от того, в каком порядке располагались составляющие его знаки. 3. Запись числа 12 будет иметь вид 111111

Правила записи чисел в непозиционных системах n n Если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой Если цифра справа меньше или равна цифре слева, то эти цифры складываются.

Недостатки непозиционных систем счисления n n n Существует постоянная потребность введения новых знаков для записи больших чисел. Невозможно представлять дробные и отрицательные числа. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения.

Позиционные системы счисления - это система, в которой значение цифры определяется ее местоположением(позицией) в изображении числа. Любая позиционная система счисления характеризуется своим основанием.

Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе. Пример: 757, 7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы. 700 + 50 + 7 + 0, 7 = 7 • 102 + 5 • 101 + 7 • 100 + 7 • 10 -1

Запись чисел в системах счисления Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения an-1 qn-1 + an-2 qn-2+. . . + a 1 q 1 + a 0 q 0 + + a-1 q-1 +. . . + a-m q-m где ai – цифры системы счисления; n и m – число целых и дробных разрядов.

Системы с основанием, целой степенью числа 2 • Двоичная (цифры 0, 1); • Восьмеричная (цифры 0, 1, . . . , 7); • Шестнадцатеричная (для первых целых чисел используются 0, 1, . . . , 9, а для следующих чисел — от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).

Примеры

Преимущества двоичной системы счисления • для реализации нужны технические устройства с двумя устойчивыми состояниями; • представление информации посредством только двух состояний надежно и помехоустойчиво; • возможно применение аппарата булевой алгебры для преобразования информации; • двоичная арифметика намного проще десятичной. Недостаток - быстрый рост числа разрядов, необходимых для записи чисел.

8 -ая и 16 -ая системы счисления Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе 8 = 23 16 = 24

Перевод 8 -ных и 16 -ных чисел в двоичную систему Достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Перевод чисел из двоичной системы в 8 -ную и 16 -ную Число нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Перевод чисел из двоичной системы в 8 -ную и 16 -ную

Перевод целого числа из десятичной системы При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q– 1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример перевода целого десятичного числа Перевести число 75 из десятичной системы в двоичную, восьмеричную : Ответ: 7510 = 1 001 0112 = 1138

Перевод числа в десятичную систему При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Примеры перевода числа в десятичную систему

Арифметические операции в позиционных системах счисления При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Сложение в двоичной системе

Арифметические операции в позиционных системах счисления Сложение в 8 -ой системе

Арифметические операции в позиционных системах счисления Сложение в 16 -ой системе

Примеры Сложить числа 15 и 6 в различных системах счисления. Ответ: 15+6 = 2110 = 101012 = 258 = 1516.

Вычитание в позиционных системах счисления Пример: Вычтем число 59, 75 из числа 201, 25.

Вычитание в позиционных системах счисления Пример: Вычтем число 59, 75 из числа 201, 25.

Умножение в позиционных системах счисления Можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения. знаков (цифр).

Умножение в позиционных системах счисления Умножение в двоичной системе

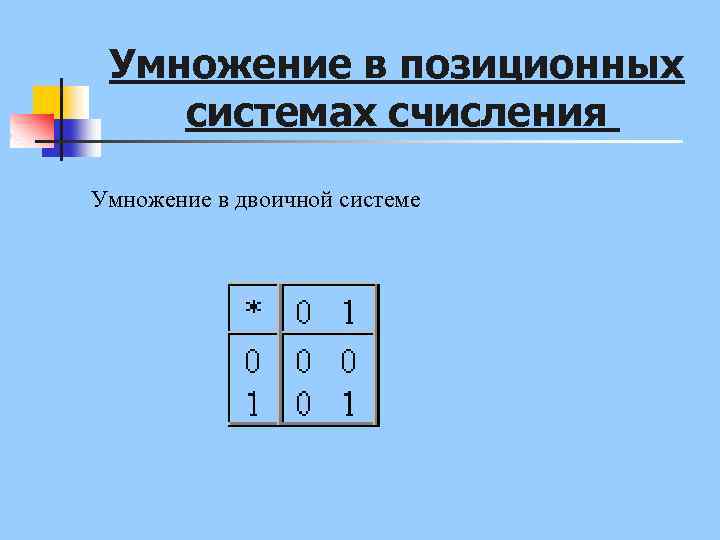Умножение в позиционных системах счисления Умножение в восьмеричной системе

Умножение в позиционных системах счисления Пример: Перемножим числа 5 и 6. Проверка: 111102 = 24 + 23 + 22 + 21 = 30; 368 = 3 • 81 + 6 • 80 = 30. Ответ: 5*6 = 3010 = 111102 = 368

Деление в позиционных системах счисления Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В 2 -ной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Деление в позиционных системах счисления Пример: Разделим число 30 на 6. Ответ: 30 : 6 = 510 = 1012 = 58