Лекция информатика 03_1_10_2011.ppt
- Количество слайдов: 132
 Информатика К. т. н. , доцент Михаил Петрович Белов
Информатика К. т. н. , доцент Михаил Петрович Белов
 Литература Основной: 1. Информатика. Базовый курс/Сост. : Симонович С. В. и др. СПб: Питер, 2010. 2. Острейковский В. А. Информатика: Учеб. для вузов. М. : Высш. школа, 2009 3. Информатика: Учебник /Под. ред. проф. Д. В. Макаровой. М. : Финансы и статистика, 2008. 4. Шафрин Ю. А. Информационные технологии. – М. : Лаборатория Базовых Знаний, 2009. 5. Кудрявцев Е. М. Mathcad 2000 Pro. – М. : ДМК Пресс, 2001. – 576 с. Дополнительный: 6. Гук М. Аппаратные средства PC: Энциклопедия. – СПб. : Питер, 2009. 7. Пятибратов А. П. , Гудыко Л. П. , Кириченко А. А. Вычислительные системы, сети и телекоммуникации. 2006.
Литература Основной: 1. Информатика. Базовый курс/Сост. : Симонович С. В. и др. СПб: Питер, 2010. 2. Острейковский В. А. Информатика: Учеб. для вузов. М. : Высш. школа, 2009 3. Информатика: Учебник /Под. ред. проф. Д. В. Макаровой. М. : Финансы и статистика, 2008. 4. Шафрин Ю. А. Информационные технологии. – М. : Лаборатория Базовых Знаний, 2009. 5. Кудрявцев Е. М. Mathcad 2000 Pro. – М. : ДМК Пресс, 2001. – 576 с. Дополнительный: 6. Гук М. Аппаратные средства PC: Энциклопедия. – СПб. : Питер, 2009. 7. Пятибратов А. П. , Гудыко Л. П. , Кириченко А. А. Вычислительные системы, сети и телекоммуникации. 2006.
 АКСИОМАТИКА ИНФОРМАТИКИ Формирование аксиоматики т. е. фундаментальных соотношений, – решающий момент в становлении любой науки. Аксиоматика вводится дедуктивным путем. Взгляд на информатику как на науку о функционировании ИР и развитии информационной среды, ее технологизации с помощью ПК позволяет сформулировать новые, не известные ранее аксиомы, не пересекающиеся с аксиоматикой других наук. В сложных системах управления управляющая подсистема имеет иерархическую структуру. Назовем наблюдателем главный, верхний элемент управляющей подсистемы. К каждому элементу управляющей подсистемы от наблюдателя идет исходный информационный поток Iисх (бит), равны Iисх = N • H (1) где N – количество сигналов (команд, документов, данных, указаний и т. п. ), исходящих от наблюдателя; Н – энтропия этих сигналов ( 0 ≤ Н ≤ 1 ). Это первая аксиома информатики.
АКСИОМАТИКА ИНФОРМАТИКИ Формирование аксиоматики т. е. фундаментальных соотношений, – решающий момент в становлении любой науки. Аксиоматика вводится дедуктивным путем. Взгляд на информатику как на науку о функционировании ИР и развитии информационной среды, ее технологизации с помощью ПК позволяет сформулировать новые, не известные ранее аксиомы, не пересекающиеся с аксиоматикой других наук. В сложных системах управления управляющая подсистема имеет иерархическую структуру. Назовем наблюдателем главный, верхний элемент управляющей подсистемы. К каждому элементу управляющей подсистемы от наблюдателя идет исходный информационный поток Iисх (бит), равны Iисх = N • H (1) где N – количество сигналов (команд, документов, данных, указаний и т. п. ), исходящих от наблюдателя; Н – энтропия этих сигналов ( 0 ≤ Н ≤ 1 ). Это первая аксиома информатики.
 Вторая аксиома информатики: информационная напряженность каждого элемента управляющей подсистемы gj определяется информационным воздействием на него наблюдателя (исходным информационным потоком) с учетом энтропии данного элемента Hj: gj = Iисх / Hj , j = 1, m (2) В содержательном аспекте энтропия любого элемента управляющей подсистемы Н, является показателем его способности к творчеству, т. е. функционированию с учетом отрицательной обратной связи с объектом. Если Hj = 1, это означает, что рассматриваемый элемент управляющей подсистемы лишь воспринимает и ретранслирует команды наблюдателя и не вырабатывает собственной информации, т. е. не осуществляет корректирующих воздействий на объект управления с учетом конкретных условий. Если Hj = 0 – управляющий элемент осуществляет управление объектом независимо от наблюдателя, полностью самостоятельно. При 0 < Hj < 1 управляющий элемент не только ретранслирует командную информацию, идущую от наблюдателя, но и вносит собственный творческий вклад в информационный потенциал управляющей подсистемы. Например, если Hj = 0, 5, то элемент в два раза усиливает направленный на него информационный поток.
Вторая аксиома информатики: информационная напряженность каждого элемента управляющей подсистемы gj определяется информационным воздействием на него наблюдателя (исходным информационным потоком) с учетом энтропии данного элемента Hj: gj = Iисх / Hj , j = 1, m (2) В содержательном аспекте энтропия любого элемента управляющей подсистемы Н, является показателем его способности к творчеству, т. е. функционированию с учетом отрицательной обратной связи с объектом. Если Hj = 1, это означает, что рассматриваемый элемент управляющей подсистемы лишь воспринимает и ретранслирует команды наблюдателя и не вырабатывает собственной информации, т. е. не осуществляет корректирующих воздействий на объект управления с учетом конкретных условий. Если Hj = 0 – управляющий элемент осуществляет управление объектом независимо от наблюдателя, полностью самостоятельно. При 0 < Hj < 1 управляющий элемент не только ретранслирует командную информацию, идущую от наблюдателя, но и вносит собственный творческий вклад в информационный потенциал управляющей подсистемы. Например, если Hj = 0, 5, то элемент в два раза усиливает направленный на него информационный поток.
 Третья аксиома информатики: информационная напряженность всей управляющей подсистемы равна сумме напряженности всех ее элементов, включая и наблюдателя: Q = ∑ gj , j = 1, m (3) где gj – информационная напряженность конкретного j го элемента; т – число элементов управляющей подсистемы. Выражение (3) не совсем точно: здесь должна быть не простая сумма, а формула, подобная выражению типа цепной реакции в ядерной физике. Четвертая аксиома информатики устанавливает соотношение между полным информационным потоком IПОЛН воздействующим на объект управления за период его перехода в новое целевое состояние, информационной напряженностью Q и энергией объекта управления Е, затрачиваемой объектом управления на переход в новое состояние: E = Q – IПОЛН (4) причем энергия имеет смысл и размерность информационной энергии. Полный информационный поток IПОЛН соответствует полезной работе управляющей подсистемы за весь период перехода объекта в новое целевое состояние. Отсюда можно качественно и количественно определить интенсивность информационной работы всей подсистемы и каждого ее элемента, отнеся ее к тому или иному отрезку времени.
Третья аксиома информатики: информационная напряженность всей управляющей подсистемы равна сумме напряженности всех ее элементов, включая и наблюдателя: Q = ∑ gj , j = 1, m (3) где gj – информационная напряженность конкретного j го элемента; т – число элементов управляющей подсистемы. Выражение (3) не совсем точно: здесь должна быть не простая сумма, а формула, подобная выражению типа цепной реакции в ядерной физике. Четвертая аксиома информатики устанавливает соотношение между полным информационным потоком IПОЛН воздействующим на объект управления за период его перехода в новое целевое состояние, информационной напряженностью Q и энергией объекта управления Е, затрачиваемой объектом управления на переход в новое состояние: E = Q – IПОЛН (4) причем энергия имеет смысл и размерность информационной энергии. Полный информационный поток IПОЛН соответствует полезной работе управляющей подсистемы за весь период перехода объекта в новое целевое состояние. Отсюда можно качественно и количественно определить интенсивность информационной работы всей подсистемы и каждого ее элемента, отнеся ее к тому или иному отрезку времени.
 Пятая аксиома информатики: работа управляющей подсистемы А (осуществление физической работы, затраты вещественно энергетических ресурсов на осуществление информационной работы) состоит из двух частей: А = а + b, где а – внутренняя работа управляющей подсистемы, затраченная на компенсацию ее исходной энтропии; b – работа, направленная на объект, т. е. усилия управляющей подсистемы на ее информационную отдачу. Согласно второму началу термодинамики (b), т. е. энтропия замкнутого пространства (системы), может только возрастать. Для осуществления обратного процесса – стабилизации и понижения энтропии – нужны компенсационные усилия. Эти компенсационные усилия затрачивает управляющая подсистема – осуществляет работу по удержанию всей системы на исходном энтропийном уровне (а). Чем выше исходная энтропия, тем большую внутреннюю работу должна осуществлять управляющая подсистема. Шестая аксиома информатики: полезная работа управляющей подсистемы (b) должна соответствовать полному информационному потоку /полн за рассматриваемый период времени.
Пятая аксиома информатики: работа управляющей подсистемы А (осуществление физической работы, затраты вещественно энергетических ресурсов на осуществление информационной работы) состоит из двух частей: А = а + b, где а – внутренняя работа управляющей подсистемы, затраченная на компенсацию ее исходной энтропии; b – работа, направленная на объект, т. е. усилия управляющей подсистемы на ее информационную отдачу. Согласно второму началу термодинамики (b), т. е. энтропия замкнутого пространства (системы), может только возрастать. Для осуществления обратного процесса – стабилизации и понижения энтропии – нужны компенсационные усилия. Эти компенсационные усилия затрачивает управляющая подсистема – осуществляет работу по удержанию всей системы на исходном энтропийном уровне (а). Чем выше исходная энтропия, тем большую внутреннюю работу должна осуществлять управляющая подсистема. Шестая аксиома информатики: полезная работа управляющей подсистемы (b) должна соответствовать полному информационному потоку /полн за рассматриваемый период времени.
 ВИДЫ И СВОЙСТВА ИНФОРМАЦИИ Как правило, свойства объектов можно разделить на два больших класса: внешние и внутренние свойства. Внутренние свойства – это свойства, Органически присущие объекту. Они обычно «скрыты» от изучающего объект и проявляют себя косвенным образом при взаимодействии данного объекта с другими. Внешние свойства – это свойства, характеризующие поведение объекта при взаимодействии с другими объектами. Поясним сказанное на примере. Масса является внутренним свойством вещества (материи). Проявляет же она себя во взаимодействии или в ходе некоторого процесса. Отсюда появляются такие понятия физики, как гравитационная масса и инерциальная масса, которые можно было бы назвать внешними свойствами вещества. Подобное разделение свойств можно привести и для информации. Для любой информации можно указать три объекта взаимодействия: источник информации, приемник информации (ее потребитель) и объект или явление, которые данная информация отражает. Поэтому можно выделить три группы внешних свойств, важнейшими из которых являются свойства информации с точки зрения потребителя. Качество информации – обобщенная положительная характеристика информации, отражающая степень ее полезности для пользователя.
ВИДЫ И СВОЙСТВА ИНФОРМАЦИИ Как правило, свойства объектов можно разделить на два больших класса: внешние и внутренние свойства. Внутренние свойства – это свойства, Органически присущие объекту. Они обычно «скрыты» от изучающего объект и проявляют себя косвенным образом при взаимодействии данного объекта с другими. Внешние свойства – это свойства, характеризующие поведение объекта при взаимодействии с другими объектами. Поясним сказанное на примере. Масса является внутренним свойством вещества (материи). Проявляет же она себя во взаимодействии или в ходе некоторого процесса. Отсюда появляются такие понятия физики, как гравитационная масса и инерциальная масса, которые можно было бы назвать внешними свойствами вещества. Подобное разделение свойств можно привести и для информации. Для любой информации можно указать три объекта взаимодействия: источник информации, приемник информации (ее потребитель) и объект или явление, которые данная информация отражает. Поэтому можно выделить три группы внешних свойств, важнейшими из которых являются свойства информации с точки зрения потребителя. Качество информации – обобщенная положительная характеристика информации, отражающая степень ее полезности для пользователя.
 Показатель качества – одно из важных положительных свойств информации (с позиции потребителя). Любое отрицательное свойство может быть заменено обратным ему, положительным. Чаще всего рассматривают показатели качества, которые можно выразить числом, и такие показатели являются количественными характеристиками положительных свойств информации. Как явствует из приведенных определений, для того, чтобы определить набор важнейших показателей качества, необходимо оценить информацию с точки зрения ее потребителя. Потребитель на практике сталкивается со следующими ситуациями: часть информации соответствует его запросу, его требованиям и такую информацию называют релевантной; а часть – нет, и ее называют нерелевантной; вся информация релевантна, но ее недостаточно для нужд потребителя; если полученной информации достаточно, то такую информацию естественно назвать полной; полученная информация несвоевременная (например, устарела); часть информации из признанной потребителем релевантной может оказаться недостоверной, т. е. содержащей скрытые ошибки (если часть ошибок потребитель обнаруживает, то он испорченную информацию попросту относит к нерелевантной); информация недоступна; информация подвержена «нежелательному» использованию и изменению со стороны других потребителей; информация имеет неудобные для потребителя форму или объем. Обзор приведенных ситуаций позволяет сформулировать следующие определения свойств информации.
Показатель качества – одно из важных положительных свойств информации (с позиции потребителя). Любое отрицательное свойство может быть заменено обратным ему, положительным. Чаще всего рассматривают показатели качества, которые можно выразить числом, и такие показатели являются количественными характеристиками положительных свойств информации. Как явствует из приведенных определений, для того, чтобы определить набор важнейших показателей качества, необходимо оценить информацию с точки зрения ее потребителя. Потребитель на практике сталкивается со следующими ситуациями: часть информации соответствует его запросу, его требованиям и такую информацию называют релевантной; а часть – нет, и ее называют нерелевантной; вся информация релевантна, но ее недостаточно для нужд потребителя; если полученной информации достаточно, то такую информацию естественно назвать полной; полученная информация несвоевременная (например, устарела); часть информации из признанной потребителем релевантной может оказаться недостоверной, т. е. содержащей скрытые ошибки (если часть ошибок потребитель обнаруживает, то он испорченную информацию попросту относит к нерелевантной); информация недоступна; информация подвержена «нежелательному» использованию и изменению со стороны других потребителей; информация имеет неудобные для потребителя форму или объем. Обзор приведенных ситуаций позволяет сформулировать следующие определения свойств информации.
 Релевантность – способность информации соответствовать нуждам (запросам) потребителя. Полнота – свойство информации исчерпывающе (для данного потребителя) характеризовать отображаемый объект и / или процесс. Своевременность – способность информации соответствовать нуждам потребителя в нужный момент времени. Достоверность – свойство информации не иметь скрытых ошибок. Доступность – свойство информации, характеризующее возможность ее получения данным потребителем. Защищенность – свойство, характеризующее невозможность несанкционированного использования или изменения. Эргономичностъ – свойство, характеризующее удобство формы или объема информации с точки зрения данного потребителя. Кроме того, информацию можно классифицировать с точки зрения ее использования на следующие виды: политическую, техническую, биологическую, химическую и т. д. Это, по существу, классификация информации по потребителю. Наконец, обобщенно характеризуя качество информации, часто используют следующее определение. Логическая, адекватно отображающая объективные закономерности природы, общества и мышления – это есть научная информация. Заметим, что последнее определение характеризует не взаимоотношение «информация – потребитель» , а взаимоотношение «информация – отражаемый объект / явление» , т. е. это уже следующая группа внешних свойств информации. Здесь наиболее важным является свойство адекватности.
Релевантность – способность информации соответствовать нуждам (запросам) потребителя. Полнота – свойство информации исчерпывающе (для данного потребителя) характеризовать отображаемый объект и / или процесс. Своевременность – способность информации соответствовать нуждам потребителя в нужный момент времени. Достоверность – свойство информации не иметь скрытых ошибок. Доступность – свойство информации, характеризующее возможность ее получения данным потребителем. Защищенность – свойство, характеризующее невозможность несанкционированного использования или изменения. Эргономичностъ – свойство, характеризующее удобство формы или объема информации с точки зрения данного потребителя. Кроме того, информацию можно классифицировать с точки зрения ее использования на следующие виды: политическую, техническую, биологическую, химическую и т. д. Это, по существу, классификация информации по потребителю. Наконец, обобщенно характеризуя качество информации, часто используют следующее определение. Логическая, адекватно отображающая объективные закономерности природы, общества и мышления – это есть научная информация. Заметим, что последнее определение характеризует не взаимоотношение «информация – потребитель» , а взаимоотношение «информация – отражаемый объект / явление» , т. е. это уже следующая группа внешних свойств информации. Здесь наиболее важным является свойство адекватности.
 Адекватность – свойство информации однозначно соответствовать отображаемому объекту или явлению. Адекватность оказывается для потребителя внутренним свойством информации, проявляющем себя через релевантность и достоверность. Среди внутренних свойств информации важнейшими являются объем (количество) информации и ее внутренняя организация, структура. По способу ее внутренней организации информацию делят на две группы: 1. Данные или простой, логически неупорядоченный набор сведений. 2. Логически упорядоченные, организованные наборы данных. Упорядоченность данных достигается наложением на данные некоторой структуры (отсюда часто используемый термин – структура данных). Во второй группе выделяют особым образом организованную информацию – знания. Знания в отличие от данных представляют собой информацию не о каком то единичном и конкретном факте, а о том, как устроены все факты определенного типа. Наконец, вне поля нашего зрения оказались свойства информации, связанные с процессом ее хранения. Здесь важнейшим свойством является живучесть – способность информации сохранять свое качество с течением времени. К этому еще можно добавить свойство уникальности. Уникальной называют информацию, хранящуюся в единственном экземпляре.
Адекватность – свойство информации однозначно соответствовать отображаемому объекту или явлению. Адекватность оказывается для потребителя внутренним свойством информации, проявляющем себя через релевантность и достоверность. Среди внутренних свойств информации важнейшими являются объем (количество) информации и ее внутренняя организация, структура. По способу ее внутренней организации информацию делят на две группы: 1. Данные или простой, логически неупорядоченный набор сведений. 2. Логически упорядоченные, организованные наборы данных. Упорядоченность данных достигается наложением на данные некоторой структуры (отсюда часто используемый термин – структура данных). Во второй группе выделяют особым образом организованную информацию – знания. Знания в отличие от данных представляют собой информацию не о каком то единичном и конкретном факте, а о том, как устроены все факты определенного типа. Наконец, вне поля нашего зрения оказались свойства информации, связанные с процессом ее хранения. Здесь важнейшим свойством является живучесть – способность информации сохранять свое качество с течением времени. К этому еще можно добавить свойство уникальности. Уникальной называют информацию, хранящуюся в единственном экземпляре.
 Тема 2 Арифметические основы компьютера
Тема 2 Арифметические основы компьютера
 Как измеряется количество информации
Как измеряется количество информации
 Задача № 1 На железнодорожном вокзале 8 путей отправления поездов. Вам сообщили, что ваш поезд прибывает на четвертый путь. Сколько информации вы получили? Решение: Из 8 путей нужно выбрать один. Поэтому N = 8, а I = 3, т. к. 8 = 23. Пояснение: номер пути (4) не влияет на количество информации, так как вероятности событий в этих задачах мы приняли считать одинаковыми. Ответ: 3 бита. Задача № 2 В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько инфор мации несет сообщение о том, что из коробки достали красный кубик? Решение: Из 16 равновероятных событий нужно выбрать одно. Поэтому N = 16, следовательно, I = 4 (16 = 24). Пояснение: события равновероятны, т. к. всех цветов в коробке присутствует по одному. Ответ: 4 бита. Задача № 3 Была получена телеграмма: «Встречайте, вагон 7» . Известно, что в составе поезда 16 вагонов. Какое количество информации было получено? Решение: Так как из 16 вагонов нужно выбрать один, то N = 16, следова тельно, = 4 (16 = 24). I Ответ: 4 бита.
Задача № 1 На железнодорожном вокзале 8 путей отправления поездов. Вам сообщили, что ваш поезд прибывает на четвертый путь. Сколько информации вы получили? Решение: Из 8 путей нужно выбрать один. Поэтому N = 8, а I = 3, т. к. 8 = 23. Пояснение: номер пути (4) не влияет на количество информации, так как вероятности событий в этих задачах мы приняли считать одинаковыми. Ответ: 3 бита. Задача № 2 В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько инфор мации несет сообщение о том, что из коробки достали красный кубик? Решение: Из 16 равновероятных событий нужно выбрать одно. Поэтому N = 16, следовательно, I = 4 (16 = 24). Пояснение: события равновероятны, т. к. всех цветов в коробке присутствует по одному. Ответ: 4 бита. Задача № 3 Была получена телеграмма: «Встречайте, вагон 7» . Известно, что в составе поезда 16 вагонов. Какое количество информации было получено? Решение: Так как из 16 вагонов нужно выбрать один, то N = 16, следова тельно, = 4 (16 = 24). I Ответ: 4 бита.

 Задача № 1 В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар. Решение: 1. Найдем вероятность того, что достали белый шар: рб = 15 / 20 = 0, 75; 2. Найдем вероятность того, что достали красный шар: рк = 5 / 20 = 0, 25. 3. Найдем количество информации в сообщении о вытаскивании белого шара: Iб = log 2 (1/рб) = log 2(1 / 0, 75) = log 21, 3 =1, 15470 бит. 4. Найдем количество информации в сообщении о вытаскивании красного шара: Iк = log 2 (1/ рк) = log 2 (1 / 0, 25) = log 24 = 2 бит. Ответ: количество информации в сообщении о том, что достали белый шар, равно 1, 1547 бит. Количество информации в сообщении о том, что достали красный шар, равно 2 бит. При сравнении ответов получается следующая ситуация: вероятность вытаскивания белого шара была больше, чем вероятность вытаскивания красного шара, а информации при этом получилось меньше. Это не случай ность, закономерная, качественная связь между вероятностью события а и количеством информации в сообщении об этом событии.
Задача № 1 В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар. Решение: 1. Найдем вероятность того, что достали белый шар: рб = 15 / 20 = 0, 75; 2. Найдем вероятность того, что достали красный шар: рк = 5 / 20 = 0, 25. 3. Найдем количество информации в сообщении о вытаскивании белого шара: Iб = log 2 (1/рб) = log 2(1 / 0, 75) = log 21, 3 =1, 15470 бит. 4. Найдем количество информации в сообщении о вытаскивании красного шара: Iк = log 2 (1/ рк) = log 2 (1 / 0, 25) = log 24 = 2 бит. Ответ: количество информации в сообщении о том, что достали белый шар, равно 1, 1547 бит. Количество информации в сообщении о том, что достали красный шар, равно 2 бит. При сравнении ответов получается следующая ситуация: вероятность вытаскивания белого шара была больше, чем вероятность вытаскивания красного шара, а информации при этом получилось меньше. Это не случай ность, закономерная, качественная связь между вероятностью события а и количеством информации в сообщении об этом событии.
 Задача № 2 В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено. Решение: 1. Всего кубиков в коробке N = 10 + 8 + 5+12 = 35. 2. Найдем вероятности: рк = 10 / 35 ≈ 0, 29, рз = 8 / 35 ≈ 0, 22, рс = 12 / 35 ≈ 0, 34, рж = 5 / 35 ≈ 0, 14. 3. Найдем количество информации: Iк = log 2( 1 / 0, 29) = log 23, 4 = 1, 85695 бит, Ic = log 2(1 / 0, 34) = log 22, 9 = 1, 71498 бит, Iз = log 2(1 / 0, 22) = log 24, 5 = 2, 132007 бит, Iж = log 2(1 / 0, 14) = log 27, 1 = 2, 672612 бит. Сравните количества информации. Ответ: наибольшее количество информации мы получим при доставании желтого кубика по причине качественной связи между вероятностью и количеством информации.
Задача № 2 В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено. Решение: 1. Всего кубиков в коробке N = 10 + 8 + 5+12 = 35. 2. Найдем вероятности: рк = 10 / 35 ≈ 0, 29, рз = 8 / 35 ≈ 0, 22, рс = 12 / 35 ≈ 0, 34, рж = 5 / 35 ≈ 0, 14. 3. Найдем количество информации: Iк = log 2( 1 / 0, 29) = log 23, 4 = 1, 85695 бит, Ic = log 2(1 / 0, 34) = log 22, 9 = 1, 71498 бит, Iз = log 2(1 / 0, 22) = log 24, 5 = 2, 132007 бит, Iж = log 2(1 / 0, 14) = log 27, 1 = 2, 672612 бит. Сравните количества информации. Ответ: наибольшее количество информации мы получим при доставании желтого кубика по причине качественной связи между вероятностью и количеством информации.
 Единицы измерения информации в технике 1 бит (binary digit – двоичный знак) – это минимальная единица измерения информации, циркулирующая в компьютере (информационный вес символа двоичного алфавита). 1 байт = 8 бит = 23; 1 маш. слово = 2 байта = 16 бит; 1 Кбайт (килобайт) = 1024 байт = 210 байт; 1 Мбайт (мегабайт) = 1024 Кбайт = 210 Кбайт = 220 байт; 1 Гбайт (гигабайт) = 1024 Мбайт = 210 Мбайт = 230 байт; 1 Тбайт (терабайт) = 1024 Гбайт = 210 Гбайт = 240 байт; 1 Пбайт (петабайт) = 1024 Тбайт = 210 Тбайт = 250 байт; 1 Эбайт (экзабайт) = 1024 Пбайт = 210 Пбайт = 260 байт; 1 Збайт (зетабайт) = 1024 Эбайт = 210 Эбайт = 270 байт; 1 Йбайт (йотабайт) = 1024 Збайт = 210 Збайт = 280 байт.
Единицы измерения информации в технике 1 бит (binary digit – двоичный знак) – это минимальная единица измерения информации, циркулирующая в компьютере (информационный вес символа двоичного алфавита). 1 байт = 8 бит = 23; 1 маш. слово = 2 байта = 16 бит; 1 Кбайт (килобайт) = 1024 байт = 210 байт; 1 Мбайт (мегабайт) = 1024 Кбайт = 210 Кбайт = 220 байт; 1 Гбайт (гигабайт) = 1024 Мбайт = 210 Мбайт = 230 байт; 1 Тбайт (терабайт) = 1024 Гбайт = 210 Гбайт = 240 байт; 1 Пбайт (петабайт) = 1024 Тбайт = 210 Тбайт = 250 байт; 1 Эбайт (экзабайт) = 1024 Пбайт = 210 Пбайт = 260 байт; 1 Збайт (зетабайт) = 1024 Эбайт = 210 Эбайт = 270 байт; 1 Йбайт (йотабайт) = 1024 Збайт = 210 Збайт = 280 байт.
 Система счисления – способ представления любого числа с помощью алфавита символов, называемых цифрами. Непозиционная система счисления В ней вводится ряд символов для представления основных чисел, а остальные числа – результат их сложения и вычитания. Основные символы для обозначения десятичных разрядов в римской системе счисления: I – один, X – десять, C – сто, M – тысяча и их половины V – пять, L – пятьдесят, D – пятьсот. Натуральные числа записываются при помощи повторения этих цифр (например, II – два, III – три, XXX – тридцать, CC – двести). Если же большая цифра стоит перед меньшей цифрой, то они складываются, если наоборот – вычитаются (например, VII – семь, IX – девять).
Система счисления – способ представления любого числа с помощью алфавита символов, называемых цифрами. Непозиционная система счисления В ней вводится ряд символов для представления основных чисел, а остальные числа – результат их сложения и вычитания. Основные символы для обозначения десятичных разрядов в римской системе счисления: I – один, X – десять, C – сто, M – тысяча и их половины V – пять, L – пятьдесят, D – пятьсот. Натуральные числа записываются при помощи повторения этих цифр (например, II – два, III – три, XXX – тридцать, CC – двести). Если же большая цифра стоит перед меньшей цифрой, то они складываются, если наоборот – вычитаются (например, VII – семь, IX – девять).
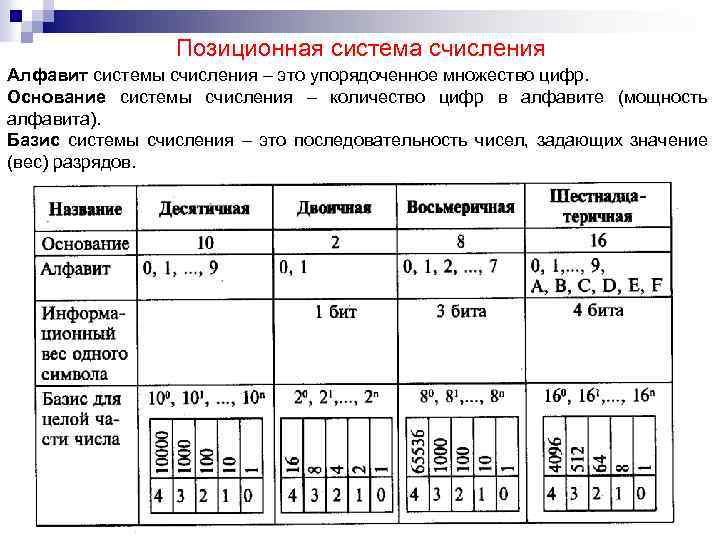 Позиционная система счисления Алфавит системы счисления – это упорядоченное множество цифр. Основание системы счисления – количество цифр в алфавите (мощность алфавита). Базис системы счисления – это последовательность чисел, задающих значение (вес) разрядов.
Позиционная система счисления Алфавит системы счисления – это упорядоченное множество цифр. Основание системы счисления – количество цифр в алфавите (мощность алфавита). Базис системы счисления – это последовательность чисел, задающих значение (вес) разрядов.
 Перевод целого числа из десятичной системы в любую другую позиционную систему счисления При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q – 1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. Пример. Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.
Перевод целого числа из десятичной системы в любую другую позиционную систему счисления При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q – 1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. Пример. Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.
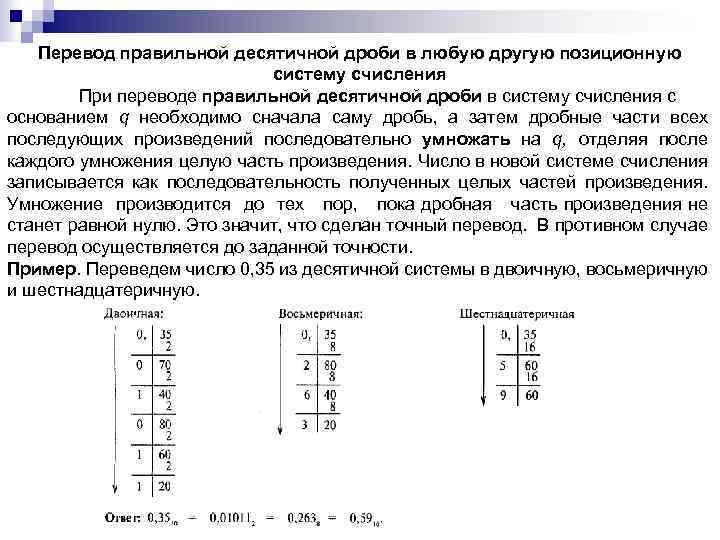 Перевод правильной десятичной дроби в любую другую позиционную систему счисления При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения. Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Пример. Переведем число 0, 35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.
Перевод правильной десятичной дроби в любую другую позиционную систему счисления При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения. Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Пример. Переведем число 0, 35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную.
 Перевод числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. Пример.
Перевод числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. Пример.
 Перевод целых чисел между системами счисления с основанием 2, 8, 16
Перевод целых чисел между системами счисления с основанием 2, 8, 16

 Правила двоичной арифметики Операция деление выполняется через последовательное умножение и вычитание.
Правила двоичной арифметики Операция деление выполняется через последовательное умножение и вычитание.
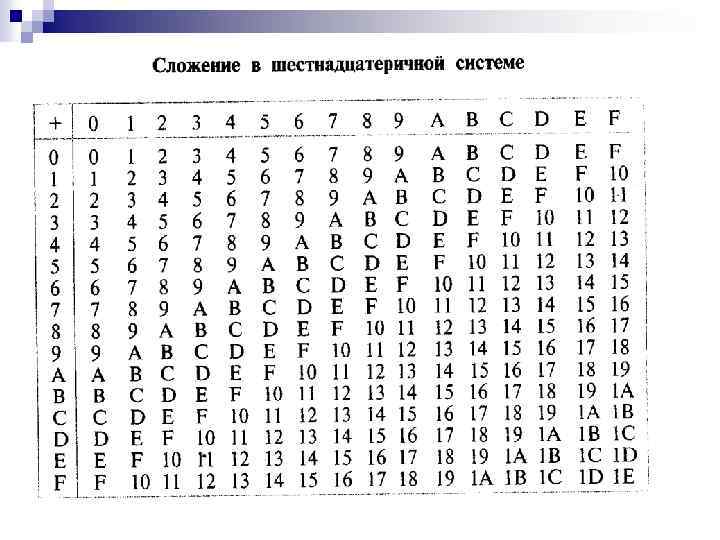
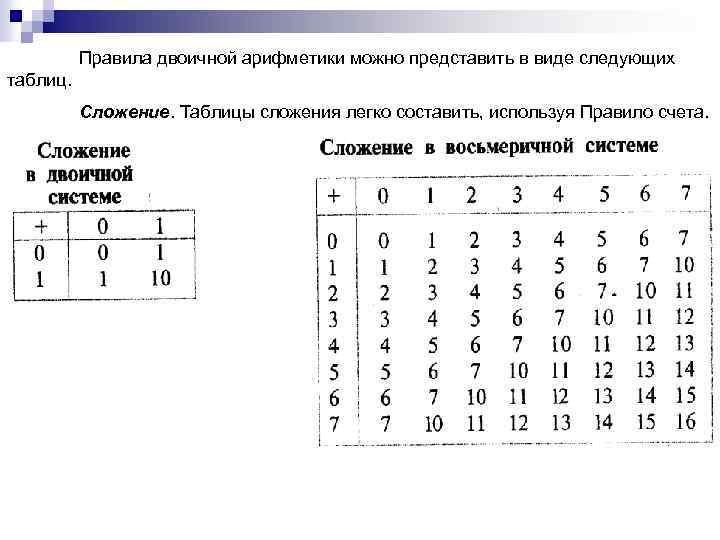 Правила двоичной арифметики можно представить в виде следующих таблиц. Сложение. Таблицы сложения легко составить, используя Правило счета.
Правила двоичной арифметики можно представить в виде следующих таблиц. Сложение. Таблицы сложения легко составить, используя Правило счета.
 При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
 Вычитание
Вычитание
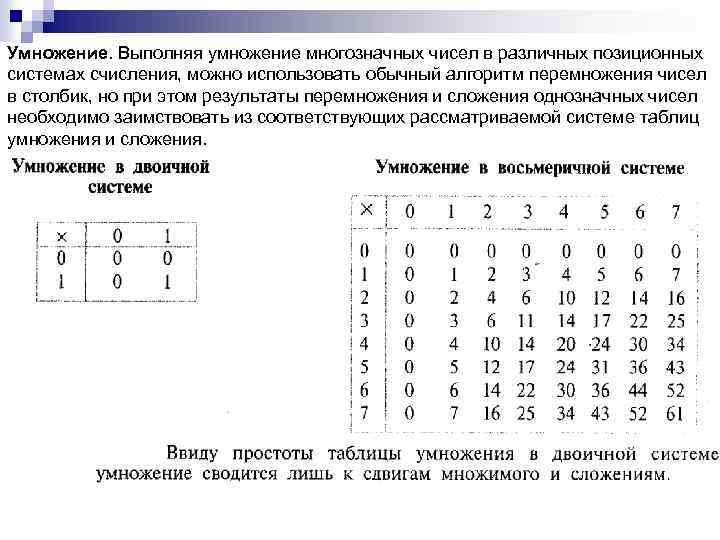 Умножение. Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение. Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
 Пример:
Пример:
 Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто: ведь очередная цифра частного может быть только нулем или единицей.
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто: ведь очередная цифра частного может быть только нулем или единицей.
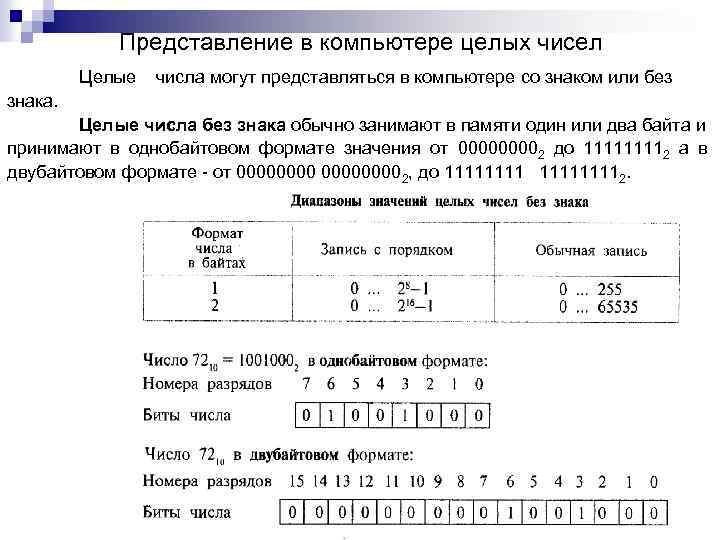 Представление в компьютере целых чисел Целые числа могут представляться в компьютере со знаком или без знака. Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00002 до 11112 а в двубайтовом формате от 000000002, до 111111112.
Представление в компьютере целых чисел Целые числа могут представляться в компьютере со знаком или без знака. Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00002 до 11112 а в двубайтовом формате от 000000002, до 111111112.
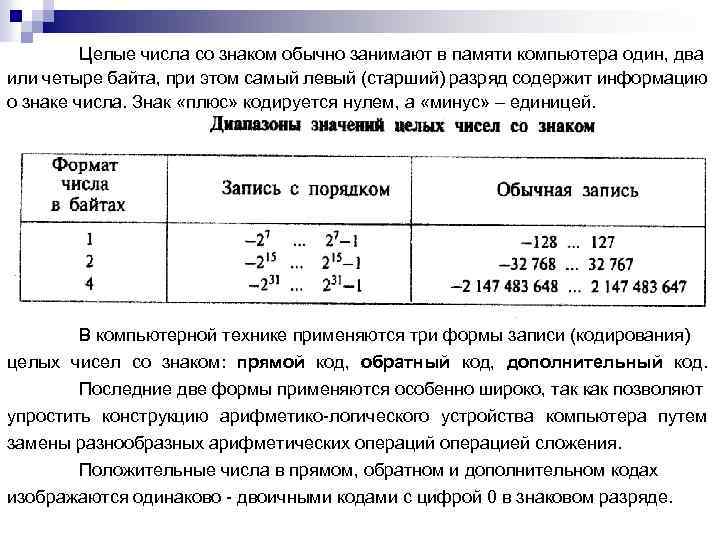 Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» – единицей. В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения. Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково двоичными кодами с цифрой 0 в знаковом разряде.
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» – единицей. В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения. Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково двоичными кодами с цифрой 0 в знаковом разряде.
 Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение. 1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа двоичный код его абсолютной величины. 2. Обратный код получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение. 1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа двоичный код его абсолютной величины. 2. Обратный код получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.
 3. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
3. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
 Представление в компьютере вещественных чисел Вещественными числами (в отличие от целых) в компьютерной технике называются числа, имеющие дробную часть. При их написании вместо запятой принято писать точку. Так, например, число 5 целое, а числа 5. 1 и 5. 0 вещественные. Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Пример. 1. 25 • 100 = 0. 125 • 101 = 0. 0125 • 102 =. . . или 12. 5 • 10 1 = 125. 0 • 10 2 = 1250. 0 • 10 3 =. . Любое число N в системе счисления с основанием q можно записать в виде N – М • qp, где М называется мантиссой числа, а р – порядком. Такой способ записи чисел называется представлением числа с плавающей точкой. Если плавающая точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т. е. максимальная точность представления числа в машине. Из этого следует, что мантисса должна быть правильной дробью, первая цифра которой отлична от нуля: M принадлежит интервалу [0. 1, 1). Такое наиболее выгодное для компьютера представление вещественных чисел называется нормализованным. Мантиссу и порядок q ичного числа принято записывать в системе с основанием q, a само основание в десятичной системе.
Представление в компьютере вещественных чисел Вещественными числами (в отличие от целых) в компьютерной технике называются числа, имеющие дробную часть. При их написании вместо запятой принято писать точку. Так, например, число 5 целое, а числа 5. 1 и 5. 0 вещественные. Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Пример. 1. 25 • 100 = 0. 125 • 101 = 0. 0125 • 102 =. . . или 12. 5 • 10 1 = 125. 0 • 10 2 = 1250. 0 • 10 3 =. . Любое число N в системе счисления с основанием q можно записать в виде N – М • qp, где М называется мантиссой числа, а р – порядком. Такой способ записи чисел называется представлением числа с плавающей точкой. Если плавающая точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т. е. максимальная точность представления числа в машине. Из этого следует, что мантисса должна быть правильной дробью, первая цифра которой отлична от нуля: M принадлежит интервалу [0. 1, 1). Такое наиболее выгодное для компьютера представление вещественных чисел называется нормализованным. Мантиссу и порядок q ичного числа принято записывать в системе с основанием q, a само основание в десятичной системе.
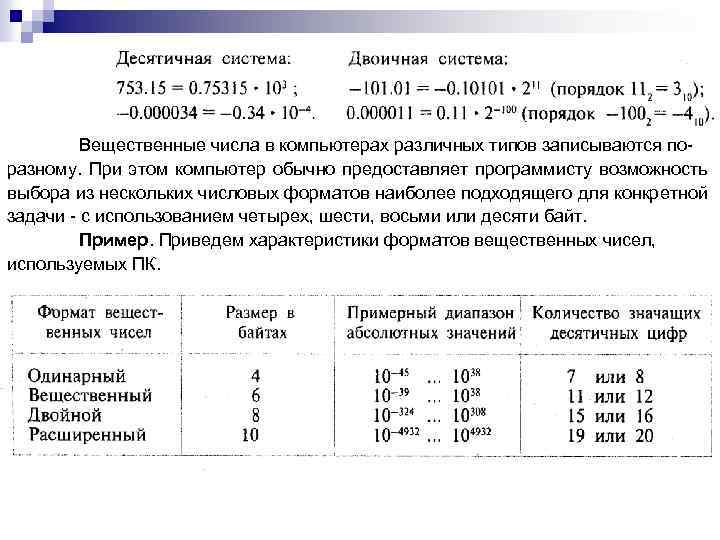 Вещественные числа в компьютерах различных типов записываются по разному. При этом компьютер обычно предоставляет программисту возможность выбора из нескольких числовых форматов наиболее подходящего для конкретной задачи с использованием четырех, шести, восьми или десяти байт. Пример. Приведем характеристики форматов вещественных чисел, используемых ПК.
Вещественные числа в компьютерах различных типов записываются по разному. При этом компьютер обычно предоставляет программисту возможность выбора из нескольких числовых форматов наиболее подходящего для конкретной задачи с использованием четырех, шести, восьми или десяти байт. Пример. Приведем характеристики форматов вещественных чисел, используемых ПК.
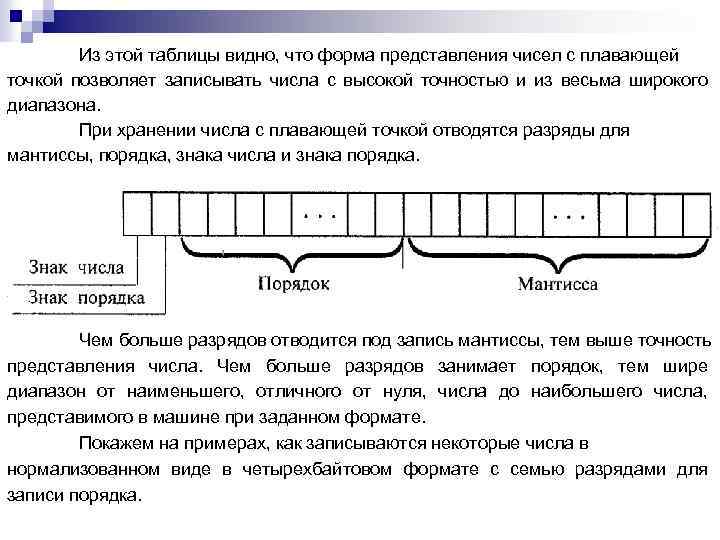 Из этой таблицы видно, что форма представления чисел с плавающей точкой позволяет записывать числа с высокой точностью и из весьма широкого диапазона. При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего, отличного от нуля, числа до наибольшего числа, представимого в машине при заданном формате. Покажем на примерах, как записываются некоторые числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка.
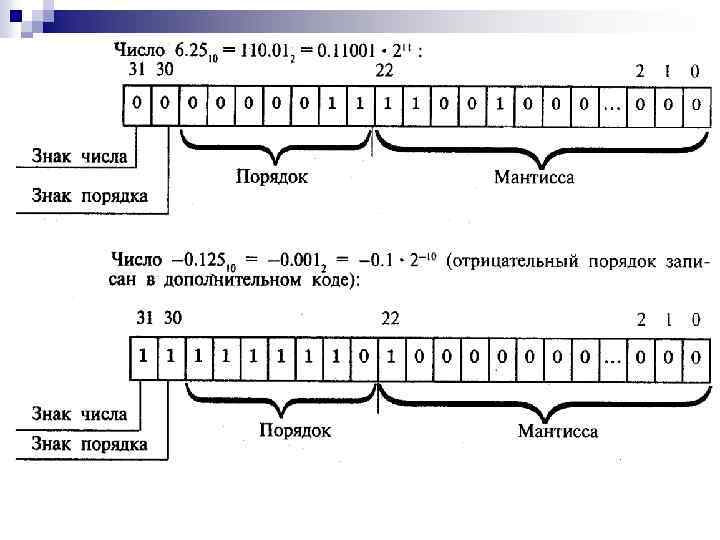
Из этой таблицы видно, что форма представления чисел с плавающей точкой позволяет записывать числа с высокой точностью и из весьма широкого диапазона. При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка. Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего, отличного от нуля, числа до наибольшего числа, представимого в машине при заданном формате. Покажем на примерах, как записываются некоторые числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка.
 Выполнение ПК арифметических действий над нормализованными числами К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ. Сложение и вычитание. При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Выполнение ПК арифметических действий над нормализованными числами К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ. Сложение и вычитание. При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
 Примеры
Примеры

 Тема 3 ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
Тема 3 ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
 ФОРМЫ МЫШЛЕНИЯ n ЛОГИКА — это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений. n Логика изучает мышление как средство познания объективного мира. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны. Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике (построение компьютеров основано на законах математической логики). В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции. n n n
ФОРМЫ МЫШЛЕНИЯ n ЛОГИКА — это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений. n Логика изучает мышление как средство познания объективного мира. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны. Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике (построение компьютеров основано на законах математической логики). В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции. n n n
 Основные формы мышления Основными формами мышления являются: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ. ПОНЯТИЕ форма мышления, в которой отражаются существенные признаки отдельного объекта или класса однородных объектов. Примеры: портфель, трапеция, ураганный ветер. Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя» . Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Основные формы мышления Основными формами мышления являются: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ. ПОНЯТИЕ форма мышления, в которой отражаются существенные признаки отдельного объекта или класса однородных объектов. Примеры: портфель, трапеция, ураганный ветер. Понятие имеет две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов. Например, содержание понятия «персональный компьютер» можно раскрыть следующим образом: «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя» . Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
 Основные формы мышления СУЖДЕНИЕ – это форма мышления, в которой что либо утверждается или отрицается об объектах, их свойствах и отношениях. Суждениями обычно являются повествовательными предложениями, которые могут быть или истинными или ложными. «Берн — столица Франции» , «Река Кубань впадает в Азовское море» , « 2>9» , « 3× 5=10» УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем новое суждение (заключение). Все металлы - простые вещества. Литий - металл. → Литий - простое вещество. Один из углов треугольника равен 90º. → Этот треугольник прямоугольный.
Основные формы мышления СУЖДЕНИЕ – это форма мышления, в которой что либо утверждается или отрицается об объектах, их свойствах и отношениях. Суждениями обычно являются повествовательными предложениями, которые могут быть или истинными или ложными. «Берн — столица Франции» , «Река Кубань впадает в Азовское море» , « 2>9» , « 3× 5=10» УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем новое суждение (заключение). Все металлы - простые вещества. Литий - металл. → Литий - простое вещество. Один из углов треугольника равен 90º. → Этот треугольник прямоугольный.
 АЛГЕБРА ВЫСКАЗЫВАНИЙ n В основе работы логических схем и устройств персонального компьютера лежит специальный математический аппарат математическая логика. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции. n Английский математик Джордж Буль (1815 — 1864 г. ) создал логическую алгебру, в которой высказывания обозначены буквами. Сочинение Джорджа Буля, в котором подробно исследовалась эта алгебра, было опубликовано в 1854 г. Оно называлось «Исследование законов мысли» ( «Investigation of the Laws of Thought» ). Отсюда ясно, что Буль рассматривал свою алгебру как инструмент изучения законов человеческого мышления, то есть законов логики. Алгебру логики иначе называют алгеброй высказываний. В математической логике суждения называются высказываниями.
АЛГЕБРА ВЫСКАЗЫВАНИЙ n В основе работы логических схем и устройств персонального компьютера лежит специальный математический аппарат математическая логика. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции. n Английский математик Джордж Буль (1815 — 1864 г. ) создал логическую алгебру, в которой высказывания обозначены буквами. Сочинение Джорджа Буля, в котором подробно исследовалась эта алгебра, было опубликовано в 1854 г. Оно называлось «Исследование законов мысли» ( «Investigation of the Laws of Thought» ). Отсюда ясно, что Буль рассматривал свою алгебру как инструмент изучения законов человеческого мышления, то есть законов логики. Алгебру логики иначе называют алгеброй высказываний. В математической логике суждения называются высказываниями.
 ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно или истинно или ложно. Например: Земля - планета Солнечной системы. (Истинно) 2+8<5 (Ложно) 5 · 5=25 (Истинно) Всякий квадрат есть параллелограмм (Истинно) Каждый параллелограмм есть квадрат (Ложно) 2 · 2 =5 (Ложно) Ш Не всякое предложение является высказыванием: 1) Восклицательные и вопросительные предложения высказываниями не являются. “Какого цвета этот дом? ” “Пейте томатный сок!” “Стоп!” 2) Не являются высказываниями и определения. “Назовем медианой отрезок, соединяющий вершину треугольника с серединой противоположной стороны”. Определения не бывают истинными или ложными, они лишь фиксируют принятое использование терминов. 3) Не являются высказываниями и предложения типа “Он сероглаз” или “х- 4 х + 3=0” в них не указано о каком человеке идет речь или для какого числа х верно равенство. Такие предложения называются высказывательными формами. Ш Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Ш
ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно или истинно или ложно. Например: Земля - планета Солнечной системы. (Истинно) 2+8<5 (Ложно) 5 · 5=25 (Истинно) Всякий квадрат есть параллелограмм (Истинно) Каждый параллелограмм есть квадрат (Ложно) 2 · 2 =5 (Ложно) Ш Не всякое предложение является высказыванием: 1) Восклицательные и вопросительные предложения высказываниями не являются. “Какого цвета этот дом? ” “Пейте томатный сок!” “Стоп!” 2) Не являются высказываниями и определения. “Назовем медианой отрезок, соединяющий вершину треугольника с серединой противоположной стороны”. Определения не бывают истинными или ложными, они лишь фиксируют принятое использование терминов. 3) Не являются высказываниями и предложения типа “Он сероглаз” или “х- 4 х + 3=0” в них не указано о каком человеке идет речь или для какого числа х верно равенство. Такие предложения называются высказывательными формами. Ш Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Ш
 Высказывания могут быть простыми и сложными. Высказывание считается простым, если никакую его часть нельзя рассматривать как отдельное высказывание Некоторые высказывания можно разложить на отдельные части, при этом каждая такая часть будет самостоятельным высказыванием. Например, высказывание “Сегодня в 4 часа дня я был в школе, а к 6 часам вечера пошел на каток” состоит из 2 частей. Высказывание может состоять и из большего количества частей. Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым. Сложное высказывание получается путем объединения простых высказываний логическими связками — НЕ, И, ИЛИ. Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок. Например, даны простые высказывания: На улице идет дождь. На улице светит солнце. На улице пасмурная погода. Составим из них сложные высказывания: На улице идет дождь и на улице светит солнце. На улице светит солнце или на улице пасмурная погода. Неверно что на улице идет дождь.
Высказывания могут быть простыми и сложными. Высказывание считается простым, если никакую его часть нельзя рассматривать как отдельное высказывание Некоторые высказывания можно разложить на отдельные части, при этом каждая такая часть будет самостоятельным высказыванием. Например, высказывание “Сегодня в 4 часа дня я был в школе, а к 6 часам вечера пошел на каток” состоит из 2 частей. Высказывание может состоять и из большего количества частей. Высказывание, которое можно разложить на части, будем называть сложным, а неразложимое далее высказывание - простым. Сложное высказывание получается путем объединения простых высказываний логическими связками — НЕ, И, ИЛИ. Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок. Например, даны простые высказывания: На улице идет дождь. На улице светит солнце. На улице пасмурная погода. Составим из них сложные высказывания: На улице идет дождь и на улице светит солнце. На улице светит солнце или на улице пасмурная погода. Неверно что на улице идет дождь.
 n n n В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0. Простые высказывания назвали логическими переменными и для простоты записи их обозначают латинскими буквами: А, В, С… Луна является спутником Земли. А = 1 Москва – столица Германии. В = 0 Сложные высказывания называются логическими функциями. Значения логической функции также может принимать значения только 0 или 1.
n n n В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0. Простые высказывания назвали логическими переменными и для простоты записи их обозначают латинскими буквами: А, В, С… Луна является спутником Земли. А = 1 Москва – столица Германии. В = 0 Сложные высказывания называются логическими функциями. Значения логической функции также может принимать значения только 0 или 1.
 БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ В алгебре высказываний, как и в обычной алгебре, вводится ряд операций. Логические связки И, ИЛИ и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.
БАЗОВЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ В алгебре высказываний, как и в обычной алгебре, вводится ряд операций. Логические связки И, ИЛИ и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.
 1. Логическая операция ИНВЕРСИЯ (ОТРИЦАНИЕ) Ш Ш Ш соответствует частице НЕ обозначается черточкой над именем переменной или знаком ¬ перед переменной Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. Таблица истинности инверсии имеет вид: A 0 1 1 0
1. Логическая операция ИНВЕРСИЯ (ОТРИЦАНИЕ) Ш Ш Ш соответствует частице НЕ обозначается черточкой над именем переменной или знаком ¬ перед переменной Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. Таблица истинности инверсии имеет вид: A 0 1 1 0
 2. Логическая операция ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) Ш соответствует союзу ИЛИ Ш обозначается знаком или ║ Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. Это определение можно обобщить для любого количества логических переменных, объединенных дизъюнкцией. А В С =0, только если А=0, В=0, С=0. Таблица истинности дизъюнкции имеет следующий вид: Ш v + v v A B АVВ 0 0 1 1 1 0 1 1
2. Логическая операция ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) Ш соответствует союзу ИЛИ Ш обозначается знаком или ║ Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. Это определение можно обобщить для любого количества логических переменных, объединенных дизъюнкцией. А В С =0, только если А=0, В=0, С=0. Таблица истинности дизъюнкции имеет следующий вид: Ш v + v v A B АVВ 0 0 1 1 1 0 1 1
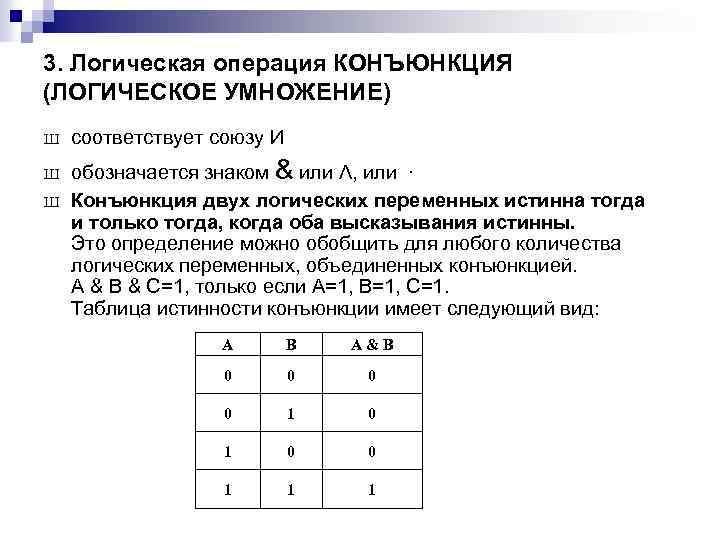 3. Логическая операция КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) Ш Ш Ш соответствует союзу И обозначается знаком & или Λ, или · Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны. Это определение можно обобщить для любого количества логических переменных, объединенных конъюнкцией. А & В & С=1, только если А=1, В=1, С=1. Таблица истинности конъюнкции имеет следующий вид: A B А&В 0 0 1 1 1
3. Логическая операция КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) Ш Ш Ш соответствует союзу И обозначается знаком & или Λ, или · Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны. Это определение можно обобщить для любого количества логических переменных, объединенных конъюнкцией. А & В & С=1, только если А=1, В=1, С=1. Таблица истинности конъюнкции имеет следующий вид: A B А&В 0 0 1 1 1
 ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ n Сложные высказывания можно записывать в виде формул. Для этого простые логические высказывания нужно обозначить как логические переменные буквами и связать их с помощью знаков логических операций. Такие формулы называются логическими выражениями. Например: n Чтобы определить значение логического выражения необходимо подставить значения логических переменных в выражение и выполнить логические операции. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.
ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ТАБЛИЦЫ ИСТИННОСТИ n Сложные высказывания можно записывать в виде формул. Для этого простые логические высказывания нужно обозначить как логические переменные буквами и связать их с помощью знаков логических операций. Такие формулы называются логическими выражениями. Например: n Чтобы определить значение логического выражения необходимо подставить значения логических переменных в выражение и выполнить логические операции. Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке: 1. инверсия; 2. конъюнкция; 3. дизъюнкция; 4. импликация и эквивалентность. Для изменения указанного порядка выполнения логических операций используются круглые скобки.
 Таблицы истинности Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных). n При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий: 1) записать выражение и определить порядок выполнения операций 2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формуле. Q=2 n , где n количество входных переменных) 3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций) 4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных. 5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности Теперь мы можем определить значение логической функции для любого набора значений логических переменных. n
Таблицы истинности Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных). n При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий: 1) записать выражение и определить порядок выполнения операций 2) определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение (определяется по формуле. Q=2 n , где n количество входных переменных) 3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций) 4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных. 5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности Теперь мы можем определить значение логической функции для любого набора значений логических переменных. n
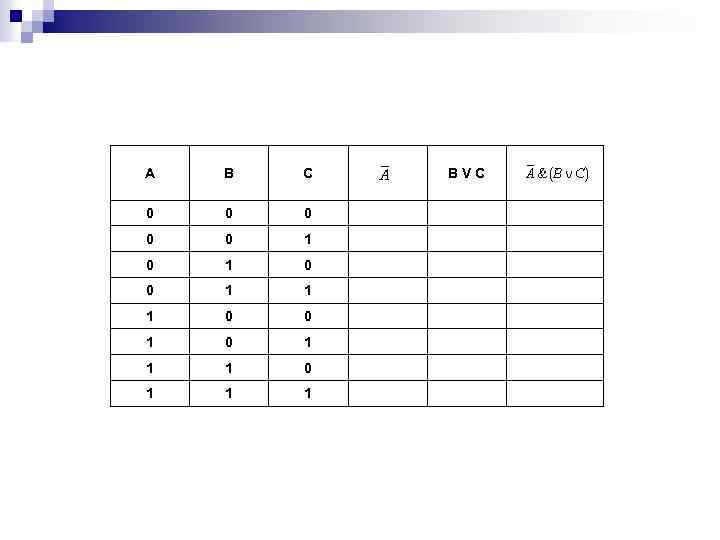
 Например, построим таблицу истинности для логической функции: Количество входных переменных в заданном выражении равно трем (A, B, C). Значит, количество входных наборов, а значит и строк Q=23=8. Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A, B, C, промежуточных результатов и (B V C), а также искомого окончательного значения сложного арифметического выражения
Например, построим таблицу истинности для логической функции: Количество входных переменных в заданном выражении равно трем (A, B, C). Значит, количество входных наборов, а значит и строк Q=23=8. Количество столбцов равно 6 (3 переменные + 3 операции). Столбцы таблицы истинности соответствуют значениям исходных выражений A, B, C, промежуточных результатов и (B V C), а также искомого окончательного значения сложного арифметического выражения
 A B C BVC
A B C BVC
 A B C 0 0 0 1 1 1 0 0 1 1 1 BVC
A B C 0 0 0 1 1 1 0 0 1 1 1 BVC
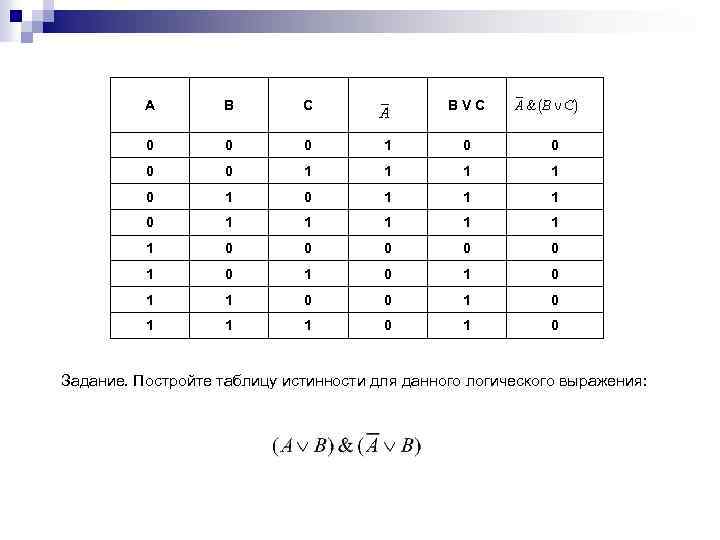 A B C BVC 0 0 0 1 1 0 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0 Задание. Постройте таблицу истинности для данного логического выражения:
A B C BVC 0 0 0 1 1 0 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0 Задание. Постройте таблицу истинности для данного логического выражения:
 А В 0 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 1 1 Равносильные логические выражения. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак =. Например:
А В 0 0 0 1 1 1 1 0 1 0 0 0 1 1 1 0 1 1 Равносильные логические выражения. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак =. Например:
 ЗАПИСЬ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ Правила построения логического выражения: 1. Для каждой строки таблицы истинности с единичным значением функции построить минтерм. Минтермом называется произведение, в котором каждая переменная встречается только один раз — либо с отрицанием, либо без него. Переменные, имеющие нулевые значения в строке, входят в минтерм с отрицанием, а переменные со значением 1 — без отрицания. 2. Объединить все минтермы операцией дизъюнкция (логическое сложение), что даст стандартную сумму произведений для заданной таблицы истинности.
ЗАПИСЬ ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ Правила построения логического выражения: 1. Для каждой строки таблицы истинности с единичным значением функции построить минтерм. Минтермом называется произведение, в котором каждая переменная встречается только один раз — либо с отрицанием, либо без него. Переменные, имеющие нулевые значения в строке, входят в минтерм с отрицанием, а переменные со значением 1 — без отрицания. 2. Объединить все минтермы операцией дизъюнкция (логическое сложение), что даст стандартную сумму произведений для заданной таблицы истинности.
 X 2 X 3 F 0 0 0 1 1 0 1 0 1 0 0 1 Построим логическое выражение для F. Найдем строки, в которых F=1. Это вторая, третья и шестая. X 1 1 Пример. Дана таблица истинности: 1 1 0 Для второй строки X 1=0, Х 2=0, X 3=1. Эту строку описывает минтерм Для третьей строки X 1=0, Х 2=1, X 3=0. Эту строку описывает минтерм Для шестой строки X 1=1, X 2=0, X 3=1. Эту строку описывает минтерм Объединяя термы, получим булево выражение F = В это выражение вошли термы произведения для строк с единичным значением функции F, а вся сумма соответствует совокупности из трех строк. Для остальных пяти наборов значений входных переменных это выражение равно нулю.
X 2 X 3 F 0 0 0 1 1 0 1 0 1 0 0 1 Построим логическое выражение для F. Найдем строки, в которых F=1. Это вторая, третья и шестая. X 1 1 Пример. Дана таблица истинности: 1 1 0 Для второй строки X 1=0, Х 2=0, X 3=1. Эту строку описывает минтерм Для третьей строки X 1=0, Х 2=1, X 3=0. Эту строку описывает минтерм Для шестой строки X 1=1, X 2=0, X 3=1. Эту строку описывает минтерм Объединяя термы, получим булево выражение F = В это выражение вошли термы произведения для строк с единичным значением функции F, а вся сумма соответствует совокупности из трех строк. Для остальных пяти наборов значений входных переменных это выражение равно нулю.
 ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ). n n Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО» . Она обозначается символом → Запись А → В читается как «из А следует В» Импликация двух высказываний истинна всегда, кроме случая, если первое высказывание истинно, а второе ложно. Таблица истинности импликации двух суждений А и В такова: А В А→В 0 0 1 1 1 В программировании эту операцию обозначают «IMP» .
ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ). n n Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО» . Она обозначается символом → Запись А → В читается как «из А следует В» Импликация двух высказываний истинна всегда, кроме случая, если первое высказывание истинно, а второе ложно. Таблица истинности импликации двух суждений А и В такова: А В А→В 0 0 1 1 1 В программировании эту операцию обозначают «IMP» .
 ЭКВИВАЛЕНТНОСТЬ (ЛОГИЧЕСКОЕ РАВЕНСТВО, ФУНКЦИЯ ТОЖДЕСТВА) n n Она обозначается символами ≡ или <=>. ( «тогда и только тогда» ). Запись А ≡ В читается как «А эквивалентно В» . Эквивалентность двух высказываний истинна только в тех случаях, когда оба высказывания ложны или оба истинны. Таблица истинности эквивалентности двух суждений А и В такова: А В А≡В 0 0 1 0 1 0 0 1 1 1 В программировании эту операцию обозначают «EQV» . В алгебре высказываний все логические функции могут быть сведены путём логических преобразований к трём базовым логическим операциям: инверсии, дизъюнкции и конъюнкции
ЭКВИВАЛЕНТНОСТЬ (ЛОГИЧЕСКОЕ РАВЕНСТВО, ФУНКЦИЯ ТОЖДЕСТВА) n n Она обозначается символами ≡ или <=>. ( «тогда и только тогда» ). Запись А ≡ В читается как «А эквивалентно В» . Эквивалентность двух высказываний истинна только в тех случаях, когда оба высказывания ложны или оба истинны. Таблица истинности эквивалентности двух суждений А и В такова: А В А≡В 0 0 1 0 1 0 0 1 1 1 В программировании эту операцию обозначают «EQV» . В алгебре высказываний все логические функции могут быть сведены путём логических преобразований к трём базовым логическим операциям: инверсии, дизъюнкции и конъюнкции
 Логические законы и правила преобразования логических выражений Равносильности формул логики высказываний часто называют законами логики. Законы логики отражают наиболее важные закономерно сти логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствие с законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям. Перечислим наиболее важные из них:
Логические законы и правила преобразования логических выражений Равносильности формул логики высказываний часто называют законами логики. Законы логики отражают наиболее важные закономерно сти логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствие с законами логики. Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям. Перечислим наиболее важные из них:
 1. Закон тождества. Всякое высказывание тождественно самому себе: Этот закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. 2. Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: Закон непротиворечия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. “Это яблоко спелое” и “Это яблоко не спелое”
1. Закон тождества. Всякое высказывание тождественно самому себе: Этот закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. 2. Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: Закон непротиворечия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. “Это яблоко спелое” и “Это яблоко не спелое”
 3. Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означа ет, что результат логического сложения высказывания и его отрицания всегда принимает значение истина: Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно, либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. 4. Закон двойного отрицания. Если дважды отрицать неко торое высказывание, то в результате мы получим исходное высказывание: Закон двойного отрицания. Отрицать отрицание какого нибудь высказывания то же, что утверждать это высказывание. “ Неверно, что 2× 2¹ 4”
3. Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означа ет, что результат логического сложения высказывания и его отрицания всегда принимает значение истина: Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно, либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. 4. Закон двойного отрицания. Если дважды отрицать неко торое высказывание, то в результате мы получим исходное высказывание: Закон двойного отрицания. Отрицать отрицание какого нибудь высказывания то же, что утверждать это высказывание. “ Неверно, что 2× 2¹ 4”
 5. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых «сомножителей» равносильна одному из них: Дизъюнкция одинаковых «слагаемых» равносильна одному: 6. Законы де Моргана: Смысл законов де Моргана (Август де Морган (1806 1871) шотландский математик и логик) можно выразить в кратких словесных формулировках: отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых; отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
5. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых «сомножителей» равносильна одному из них: Дизъюнкция одинаковых «слагаемых» равносильна одному: 6. Законы де Моргана: Смысл законов де Моргана (Август де Морган (1806 1871) шотландский математик и логик) можно выразить в кратких словесных формулировках: отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых; отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
 . 7 Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказыва ний можно менять местами логические переменные при опе рацияхлогического умножения и логического сложения: Логическое умножение: Логическое сложение: . 8 Правило ассоциативности. Если в логическом выраже нии используются только операция логического умножения или только операция логического сложения, то можно пре небрегать скобками или произвольно их расставлять: Логическое умножение: Логическое сложение:
. 7 Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказыва ний можно менять местами логические переменные при опе рацияхлогического умножения и логического сложения: Логическое умножение: Логическое сложение: . 8 Правило ассоциативности. Если в логическом выраже нии используются только операция логического умножения или только операция логического сложения, то можно пре небрегать скобками или произвольно их расставлять: Логическое умножение: Логическое сложение:
 9. Правило дистрибутивности. В отличие от обычной алгеб ры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки, как общие множители, так и общие слагаемые: Дистрибутивность умножения относительно сложения: Дистрибутивность сложения относительно умножения: 10. 11. 12. Законы поглощения:
9. Правило дистрибутивности. В отличие от обычной алгеб ры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки, как общие множители, так и общие слагаемые: Дистрибутивность умножения относительно сложения: Дистрибутивность сложения относительно умножения: 10. 11. 12. Законы поглощения:
 РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
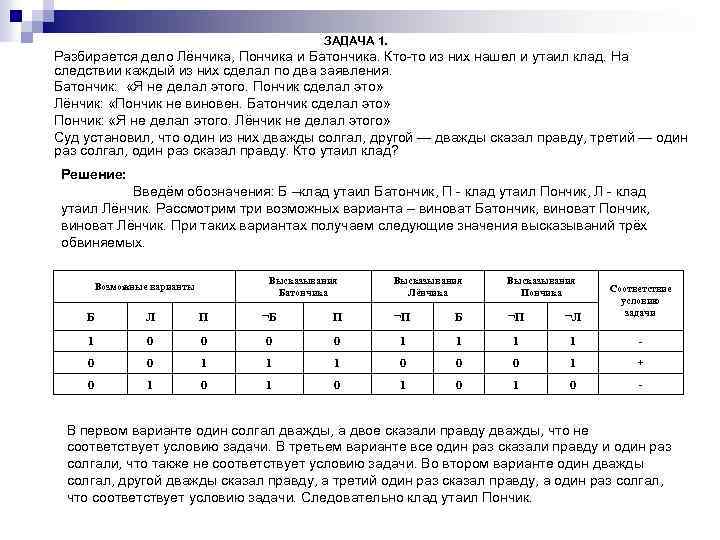 ЗАДАЧА 1. Разбирается дело Лёнчика, Пончика и Батончика. Кто то из них нашел и утаил клад. На следствии каждый из них сделал по два заявления. Батончик: «Я не делал этого. Пончик сделал это» Лёнчик: «Пончик не виновен. Батончик сделал это» Пончик: «Я не делал этого. Лёнчик не делал этого» Суд установил, что один из них дважды солгал, другой — дважды сказал правду, третий — один раз солгал, один раз сказал правду. Кто утаил клад? Решение: Введём обозначения: Б –клад утаил Батончик, П клад утаил Пончик, Л клад утаил Лёнчик. Рассмотрим три возможных варианта – виноват Батончик, виноват Пончик, виноват Лёнчик. При таких вариантах получаем следующие значения высказываний трёх обвиняемых. Высказывания Батончика Возможные варианты Высказывания Лёнчика Высказывания Пончика Соответствие условию задачи Б Л П ¬Б П ¬П Б ¬П ¬Л 1 0 0 1 1 - 0 0 1 1 1 0 0 0 1 + 0 1 0 1 0 - В первом варианте один солгал дважды, а двое сказали правду дважды, что не соответствует условию задачи. В третьем варианте все один раз сказали правду и один раз солгали, что также не соответствует условию задачи. Во втором варианте один дважды солгал, другой дважды сказал правду, а третий один раз сказал правду, а один раз солгал, что соответствует условию задачи. Следовательно клад утаил Пончик.
ЗАДАЧА 1. Разбирается дело Лёнчика, Пончика и Батончика. Кто то из них нашел и утаил клад. На следствии каждый из них сделал по два заявления. Батончик: «Я не делал этого. Пончик сделал это» Лёнчик: «Пончик не виновен. Батончик сделал это» Пончик: «Я не делал этого. Лёнчик не делал этого» Суд установил, что один из них дважды солгал, другой — дважды сказал правду, третий — один раз солгал, один раз сказал правду. Кто утаил клад? Решение: Введём обозначения: Б –клад утаил Батончик, П клад утаил Пончик, Л клад утаил Лёнчик. Рассмотрим три возможных варианта – виноват Батончик, виноват Пончик, виноват Лёнчик. При таких вариантах получаем следующие значения высказываний трёх обвиняемых. Высказывания Батончика Возможные варианты Высказывания Лёнчика Высказывания Пончика Соответствие условию задачи Б Л П ¬Б П ¬П Б ¬П ¬Л 1 0 0 1 1 - 0 0 1 1 1 0 0 0 1 + 0 1 0 1 0 - В первом варианте один солгал дважды, а двое сказали правду дважды, что не соответствует условию задачи. В третьем варианте все один раз сказали правду и один раз солгали, что также не соответствует условию задачи. Во втором варианте один дважды солгал, другой дважды сказал правду, а третий один раз сказал правду, а один раз солгал, что соответствует условию задачи. Следовательно клад утаил Пончик.
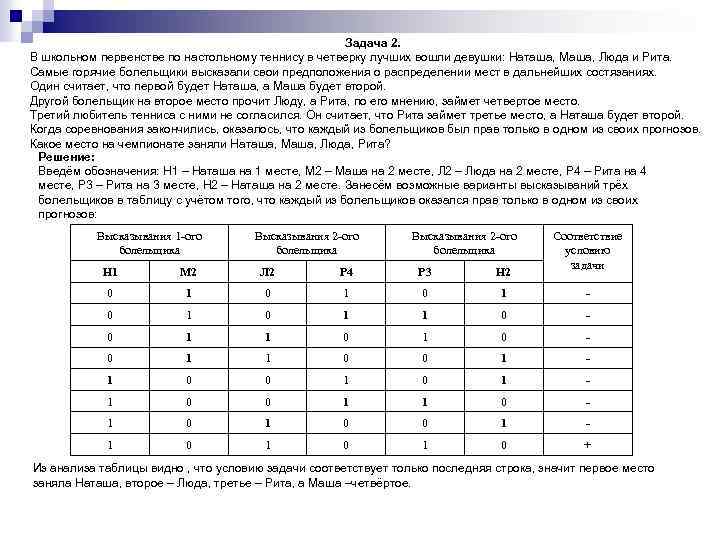 Задача 2. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях. Один считает, что первой будет Наташа, а Маша будет второй. Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй. Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита? Решение: Введём обозначения: Н 1 – Наташа на 1 месте, М 2 – Маша на 2 месте, Л 2 – Люда на 2 месте, Р 4 – Рита на 4 месте, Р 3 – Рита на 3 месте, Н 2 – Наташа на 2 месте. Занесём возможные варианты высказываний трёх болельщиков в таблицу с учётом того, что каждый из болельщиков оказался прав только в одном из своих прогнозов: Высказывания 1 -ого болельщика Высказывания 2 -ого болельщика Соответствие условию задачи Н 1 М 2 Л 2 Р 4 Р 3 Н 2 0 1 0 1 - 0 1 1 0 0 1 - 1 0 0 1 1 0 - 1 0 0 1 - 1 0 1 0 + Из анализа таблицы видно , что условию задачи соответствует только последняя строка, значит первое место заняла Наташа, второе – Люда, третье – Рита, а Маша –четвёртое.
Задача 2. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях. Один считает, что первой будет Наташа, а Маша будет второй. Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй. Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита? Решение: Введём обозначения: Н 1 – Наташа на 1 месте, М 2 – Маша на 2 месте, Л 2 – Люда на 2 месте, Р 4 – Рита на 4 месте, Р 3 – Рита на 3 месте, Н 2 – Наташа на 2 месте. Занесём возможные варианты высказываний трёх болельщиков в таблицу с учётом того, что каждый из болельщиков оказался прав только в одном из своих прогнозов: Высказывания 1 -ого болельщика Высказывания 2 -ого болельщика Соответствие условию задачи Н 1 М 2 Л 2 Р 4 Р 3 Н 2 0 1 0 1 - 0 1 1 0 0 1 - 1 0 0 1 1 0 - 1 0 0 1 - 1 0 1 0 + Из анализа таблицы видно , что условию задачи соответствует только последняя строка, значит первое место заняла Наташа, второе – Люда, третье – Рита, а Маша –четвёртое.
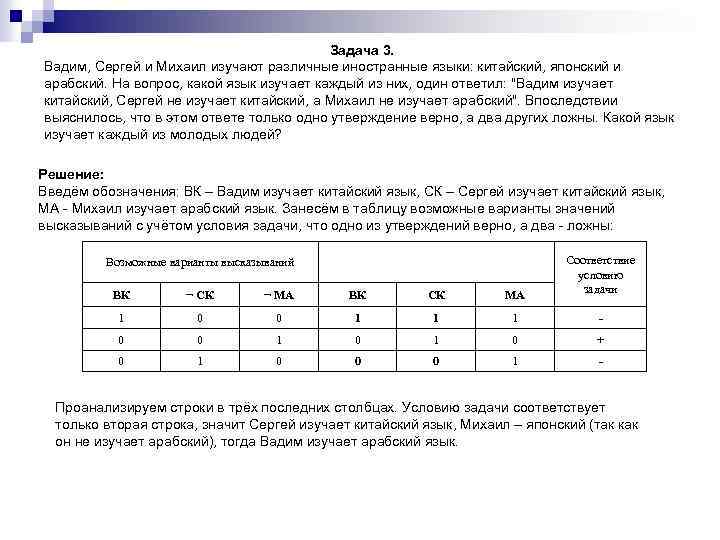 Задача 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение: Введём обозначения: ВК – Вадим изучает китайский язык, СК – Сергей изучает китайский язык, МА Михаил изучает арабский язык. Занесём в таблицу возможные варианты значений высказываний с учётом условия задачи, что одно из утверждений верно, а два ложны: Возможные варианты высказываний Соответствие условию задачи ВК ¬ СК ¬ МА ВК СК МА 1 0 0 1 1 1 - 0 0 1 0 + 0 1 0 0 0 1 - Проанализируем строки в трёх последних столбцах. Условию задачи соответствует только вторая строка, значит Сергей изучает китайский язык, Михаил – японский (так как он не изучает арабский), тогда Вадим изучает арабский язык.
Задача 3. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение: Введём обозначения: ВК – Вадим изучает китайский язык, СК – Сергей изучает китайский язык, МА Михаил изучает арабский язык. Занесём в таблицу возможные варианты значений высказываний с учётом условия задачи, что одно из утверждений верно, а два ложны: Возможные варианты высказываний Соответствие условию задачи ВК ¬ СК ¬ МА ВК СК МА 1 0 0 1 1 1 - 0 0 1 0 + 0 1 0 0 0 1 - Проанализируем строки в трёх последних столбцах. Условию задачи соответствует только вторая строка, значит Сергей изучает китайский язык, Михаил – японский (так как он не изучает арабский), тогда Вадим изучает арабский язык.
 Задача 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия. Решение: Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение). Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист. Имя Юра Профессия врач Увлечение туризм Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем: Имя Юра Тимур Влад Профессия физик врач юрист Увлечение бег туризм регби Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
Задача 4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия. Решение: Здесь исходные данные разбиваются на тройки (имя — профессия — увлечение). Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист. Имя Юра Профессия врач Увлечение туризм Буква "а", присутствующая в слове "врач", указывает на то, что Влад тоже не врач, следовательно врач — Тимур. В его имени есть буквы "т" и "р", встречающиеся в слове "туризм", следовательно второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени — Юра не юрист и не регбист, так как в его имени содержатся буквы "ю" и "р". Следовательно, окончательно имеем: Имя Юра Тимур Влад Профессия физик врач юрист Увлечение бег туризм регби Ответ. Влад — юрист и регбист, Тимур — врач и турист, Юра — физик и бегун.
 ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
 Логические элементы В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Знания из области математической логики можно использовать для конструирования различных электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого то предмета нашего мира, условно называемых "ложь" и "истина". Таким предметом, имеющим два фиксированных состояния, может быть электрический ток. Были созданы устройства управления электричеством электронные схемы, состоящие из набора полупроводниковых элементов. Такие электронные схемы, которые преобразовывают сигналы только двух фиксированных напряжений электрического тока стали называть логическими элементами. Логические элементы — это электронные устройства, которые преобразуют проходящие через них двоичные электрические сигналы по определенному закону. Логические элементы имеют один или несколько входов, на которые подаются электрические сигналы, обозначаемые условно 0, если отсутствует электрический сигнал, и 1, если имеется электрический сигнал. Также логические элементы имеют один выход, с которого снимается преобразованный электрический сигнал. Было доказано, что все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.
Логические элементы В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Знания из области математической логики можно использовать для конструирования различных электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого то предмета нашего мира, условно называемых "ложь" и "истина". Таким предметом, имеющим два фиксированных состояния, может быть электрический ток. Были созданы устройства управления электричеством электронные схемы, состоящие из набора полупроводниковых элементов. Такие электронные схемы, которые преобразовывают сигналы только двух фиксированных напряжений электрического тока стали называть логическими элементами. Логические элементы — это электронные устройства, которые преобразуют проходящие через них двоичные электрические сигналы по определенному закону. Логические элементы имеют один или несколько входов, на которые подаются электрические сигналы, обозначаемые условно 0, если отсутствует электрический сигнал, и 1, если имеется электрический сигнал. Также логические элементы имеют один выход, с которого снимается преобразованный электрический сигнал. Было доказано, что все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.
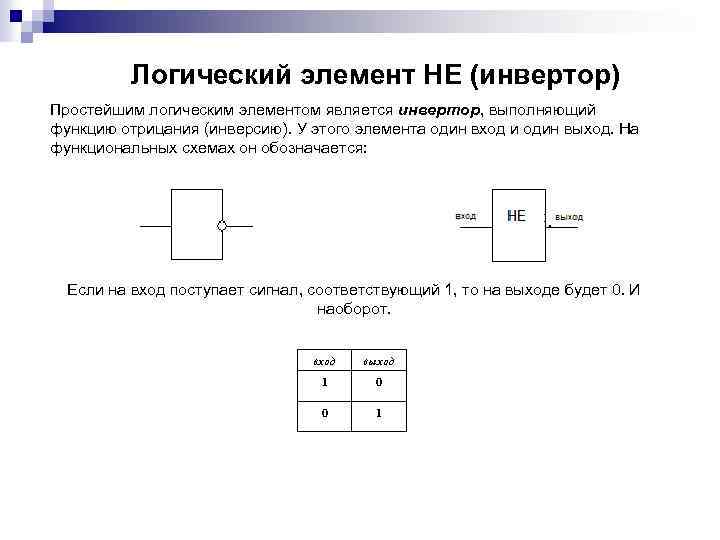 Логический элемент НЕ (инвертор) Простейшим логическим элементом является инвертор, выполняющий функцию отрицания (инверсию). У этого элемента один вход и один выход. На функциональных схемах он обозначается: Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. вход выход 1 0 0 1
Логический элемент НЕ (инвертор) Простейшим логическим элементом является инвертор, выполняющий функцию отрицания (инверсию). У этого элемента один вход и один выход. На функциональных схемах он обозначается: Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. вход выход 1 0 0 1
 Логический элемент ИЛИ (дизъюнктор) Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается: Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1. вход 1 вход 2 выход 0 0 1 1 1 0 1 1
Логический элемент ИЛИ (дизъюнктор) Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается: Если хотя бы на один вход поступает сигнал 1, то на выходе будет сигнал 1. вход 1 вход 2 выход 0 0 1 1 1 0 1 1
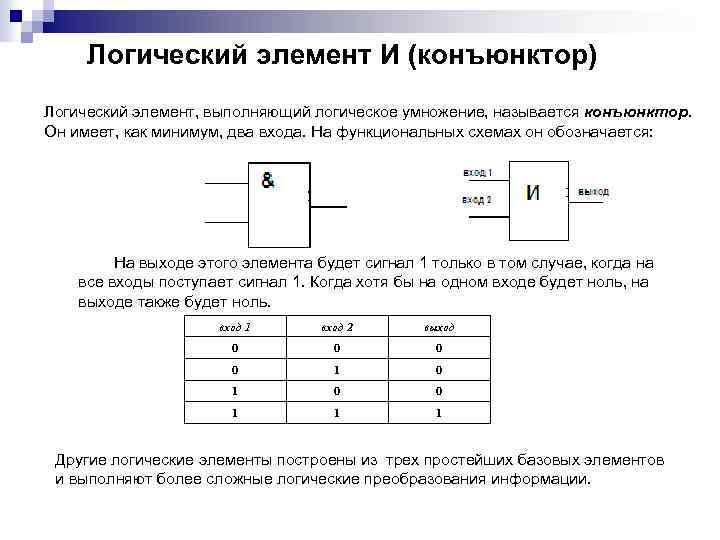 Логический элемент И (конъюнктор) Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается: На выходе этого элемента будет сигнал 1 только в том случае, когда на все входы поступает сигнал 1. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. выход вход 1 вход 2 0 0 1 1 1 Другие логические элементы построены из трех простейших базовых элементов и выполняют более сложные логические преобразования информации.
Логический элемент И (конъюнктор) Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается: На выходе этого элемента будет сигнал 1 только в том случае, когда на все входы поступает сигнал 1. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. выход вход 1 вход 2 0 0 1 1 1 Другие логические элементы построены из трех простейших базовых элементов и выполняют более сложные логические преобразования информации.
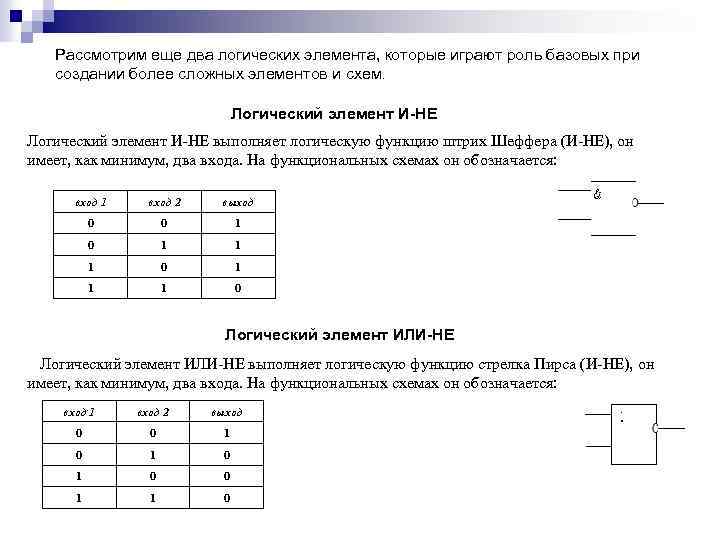 Рассмотрим еще два логических элемента, которые играют роль базовых при создании более сложных элементов и схем. Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (И-НЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается: вход 1 вход 2 выход 0 0 1 1 1 0 Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (И-НЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается: вход. 1 вход 2 выход 0 0 1 0 1 0 0 1 1 0
Рассмотрим еще два логических элемента, которые играют роль базовых при создании более сложных элементов и схем. Логический элемент И-НЕ выполняет логическую функцию штрих Шеффера (И-НЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается: вход 1 вход 2 выход 0 0 1 1 1 0 Логический элемент ИЛИ-НЕ выполняет логическую функцию стрелка Пирса (И-НЕ), он имеет, как минимум, два входа. На функциональных схемах он обозначается: вход. 1 вход 2 выход 0 0 1 0 1 0 0 1 1 0
 Функциональные схемы Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов — функциональные схемы. Функциональная (логическая) схема – это схема, состоящая из логических элементов, которая выполняет определённую функцию. Анализируя функциональную схему, можно понять, как работает логическое устройство, т. е. дать ответ на вопрос: какую функцию она выполняет. Важной формой описания функциональных схем является структурная формула. Покажем на примере, как выписывают формулу по заданной функциональной схеме. Ясно, что элемент “И” осуществляет логическое умножение значений ¬А и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т. е. вычисляется значение выражения: Таким образом структурной формулой данной функциональной схемы является формула:
Функциональные схемы Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов — функциональные схемы. Функциональная (логическая) схема – это схема, состоящая из логических элементов, которая выполняет определённую функцию. Анализируя функциональную схему, можно понять, как работает логическое устройство, т. е. дать ответ на вопрос: какую функцию она выполняет. Важной формой описания функциональных схем является структурная формула. Покажем на примере, как выписывают формулу по заданной функциональной схеме. Ясно, что элемент “И” осуществляет логическое умножение значений ¬А и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т. е. вычисляется значение выражения: Таким образом структурной формулой данной функциональной схемы является формула:
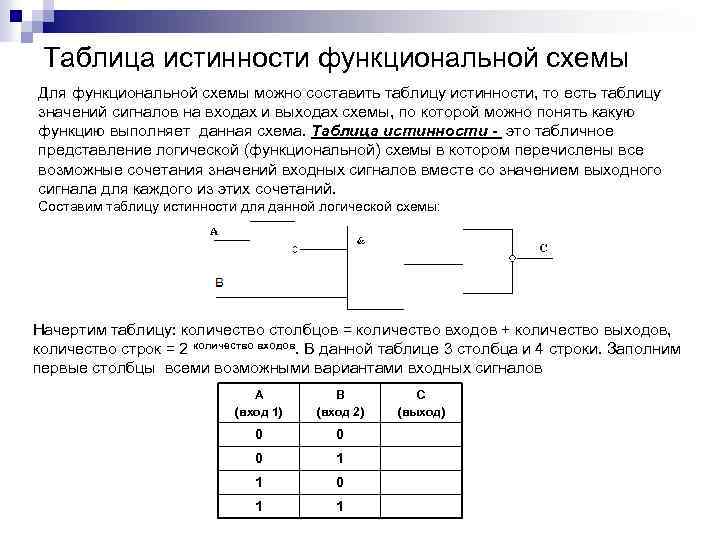 Таблица истинности функциональной схемы Для функциональной схемы можно составить таблицу истинности, то есть таблицу значений сигналов на входах и выходах схемы, по которой можно понять какую функцию выполняет данная схема. Таблица истинности - это табличное представление логической (функциональной) схемы в котором перечислены все возможные сочетания значений входных сигналов вместе со значением выходного сигнала для каждого из этих сочетаний. Составим таблицу истинности для данной логической схемы: Начертим таблицу: количество столбцов = количество входов + количество выходов, количество строк = 2 количество входов. В данной таблице 3 столбца и 4 строки. Заполним первые столбцы всеми возможными вариантами входных сигналов А (вход 1) В (вход 2) 0 0 0 1 1 С (выход)
Таблица истинности функциональной схемы Для функциональной схемы можно составить таблицу истинности, то есть таблицу значений сигналов на входах и выходах схемы, по которой можно понять какую функцию выполняет данная схема. Таблица истинности - это табличное представление логической (функциональной) схемы в котором перечислены все возможные сочетания значений входных сигналов вместе со значением выходного сигнала для каждого из этих сочетаний. Составим таблицу истинности для данной логической схемы: Начертим таблицу: количество столбцов = количество входов + количество выходов, количество строк = 2 количество входов. В данной таблице 3 столбца и 4 строки. Заполним первые столбцы всеми возможными вариантами входных сигналов А (вход 1) В (вход 2) 0 0 0 1 1 С (выход)
 Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу. Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=0), запишем в таблицу. Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
Рассмотрим первый вариант входных сигналов: А=0, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу. Рассмотрим второй вариант входных сигналов: А=0, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=0), запишем в таблицу. Рассмотрим третий вариант входных сигналов: А=1, В=0. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу.
 Рассмотрим четвёртый вариант входных сигналов: А=1, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу. В результате получаем таблицу истинности данной логической схемы: А (вход 1) В (вход 2) С (выход) 0 0 1 0 1 1 1 1 Задание. Построить таблицу истинности для данной логической схемы и записать формулу для данной схемы:
Рассмотрим четвёртый вариант входных сигналов: А=1, В=1. Проследим по схеме, как проходят и преобразуются входные сигналы. Результат, полученный на выходе (С=1), запишем в таблицу. В результате получаем таблицу истинности данной логической схемы: А (вход 1) В (вход 2) С (выход) 0 0 1 0 1 1 1 1 Задание. Построить таблицу истинности для данной логической схемы и записать формулу для данной схемы:
 Логическая реализация типовых устройств компьютера Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико логическое устройство (АЛУ). Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры, полусумматоры, шифраторы, дешифраторы, счетчики, регистры. Выясним , как из логических элементов разрабатываются логические устройства.
Логическая реализация типовых устройств компьютера Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико логическое устройство (АЛУ). Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры, полусумматоры, шифраторы, дешифраторы, счетчики, регистры. Выясним , как из логических элементов разрабатываются логические устройства.
 Этапы конструирования логического устройства. Конструирование логического устройства состоит из следующих этапов: 1. Построение таблицы истинности по заданным условиям работы проектируемого узла (т. е. по соответствию его входных и выходных сигналов). 2. Конструирование логической функции данного узла по таблице истинности, ее преобразование (упрощение), если это возможно и необходимо. 3. Составление функциональной схемы проектируемого узла по формуле логической функции. После этого остается только реализовать полученную схему.
Этапы конструирования логического устройства. Конструирование логического устройства состоит из следующих этапов: 1. Построение таблицы истинности по заданным условиям работы проектируемого узла (т. е. по соответствию его входных и выходных сигналов). 2. Конструирование логической функции данного узла по таблице истинности, ее преобразование (упрощение), если это возможно и необходимо. 3. Составление функциональной схемы проектируемого узла по формуле логической функции. После этого остается только реализовать полученную схему.
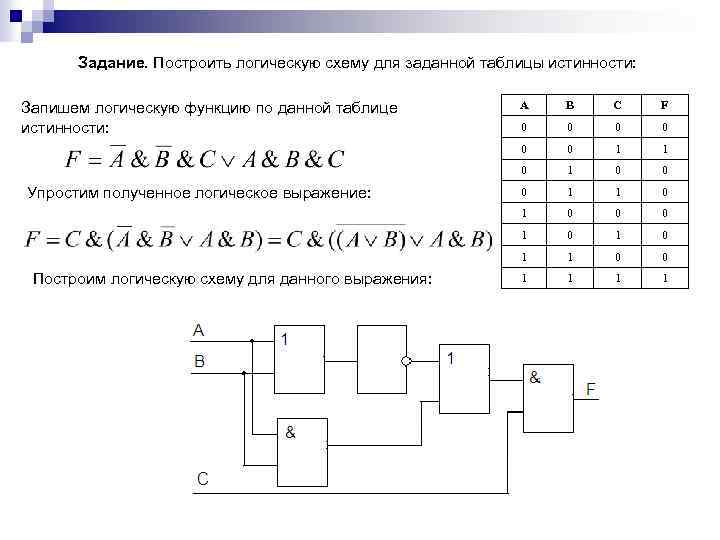 Задание. Построить логическую схему для заданной таблицы истинности: С F 0 0 0 1 1 1 0 0 0 1 0 1 Построим логическую схему для данного выражения: В 0 Упростим полученное логическое выражение: А 0 Запишем логическую функцию по данной таблице истинности: 1 0 0 1 1
Задание. Построить логическую схему для заданной таблицы истинности: С F 0 0 0 1 1 1 0 0 0 1 0 1 Построим логическую схему для данного выражения: В 0 Упростим полученное логическое выражение: А 0 Запишем логическую функцию по данной таблице истинности: 1 0 0 1 1
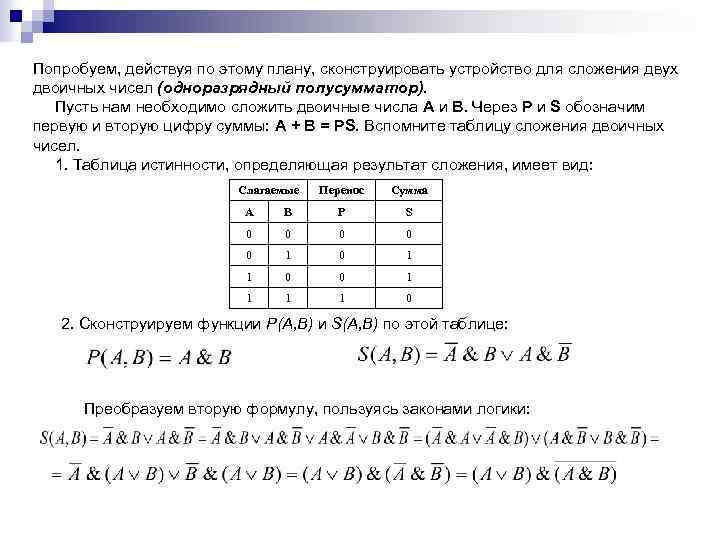 Попробуем, действуя по этому плану, сконструировать устройство для сложения двух двоичных чисел (одноразрядный полусумматор). Пусть нам необходимо сложить двоичные числа А и В. Через P и S обозначим первую и вторую цифру суммы: A + B = PS. Вспомните таблицу сложения двоичных чисел. 1. Таблица истинности, определяющая результат сложения, имеет вид: Слагаемые Перенос Сумма А В Р S 0 0 0 1 1 0 2. Сконструируем функции P(A, B) и S(A, B) по этой таблице: Преобразуем вторую формулу, пользуясь законами логики:
Попробуем, действуя по этому плану, сконструировать устройство для сложения двух двоичных чисел (одноразрядный полусумматор). Пусть нам необходимо сложить двоичные числа А и В. Через P и S обозначим первую и вторую цифру суммы: A + B = PS. Вспомните таблицу сложения двоичных чисел. 1. Таблица истинности, определяющая результат сложения, имеет вид: Слагаемые Перенос Сумма А В Р S 0 0 0 1 1 0 2. Сконструируем функции P(A, B) и S(A, B) по этой таблице: Преобразуем вторую формулу, пользуясь законами логики:
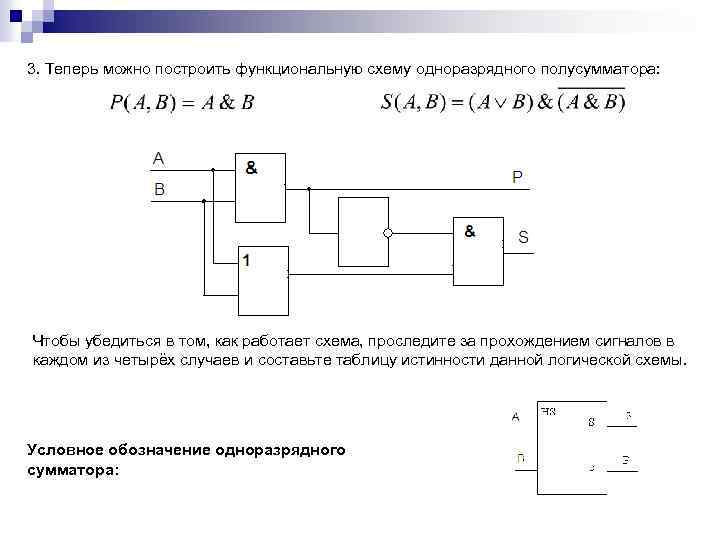 3. Теперь можно построить функциональную схему одноразрядного полусумматора: Чтобы убедиться в том, как работает схема, проследите за прохождением сигналов в каждом из четырёх случаев и составьте таблицу истинности данной логической схемы. Условное обозначение одноразрядного сумматора:
3. Теперь можно построить функциональную схему одноразрядного полусумматора: Чтобы убедиться в том, как работает схема, проследите за прохождением сигналов в каждом из четырёх случаев и составьте таблицу истинности данной логической схемы. Условное обозначение одноразрядного сумматора:
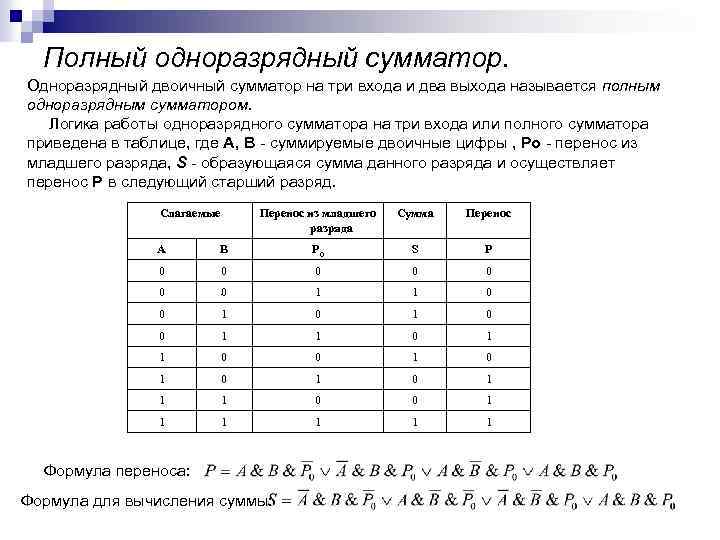 Полный одноразрядный сумматор. Одноразрядный двоичный сумматор на три входа и два выхода называется полным одноразрядным сумматором. Логика работы одноразрядного сумматора на три входа или полного сумматора приведена в таблице, где А, В суммируемые двоичные цифры , Pо перенос из младшего разряда, S образующаяся сумма данного разряда и осуществляет перенос P в следующий старший разряд. Слагаемые Перенос из младшего разряда Сумма Перенос А B P 0 S P 0 0 0 . 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 Формула переноса: Формула для вычисления суммы:
Полный одноразрядный сумматор. Одноразрядный двоичный сумматор на три входа и два выхода называется полным одноразрядным сумматором. Логика работы одноразрядного сумматора на три входа или полного сумматора приведена в таблице, где А, В суммируемые двоичные цифры , Pо перенос из младшего разряда, S образующаяся сумма данного разряда и осуществляет перенос P в следующий старший разряд. Слагаемые Перенос из младшего разряда Сумма Перенос А B P 0 S P 0 0 0 . 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 Формула переноса: Формула для вычисления суммы:
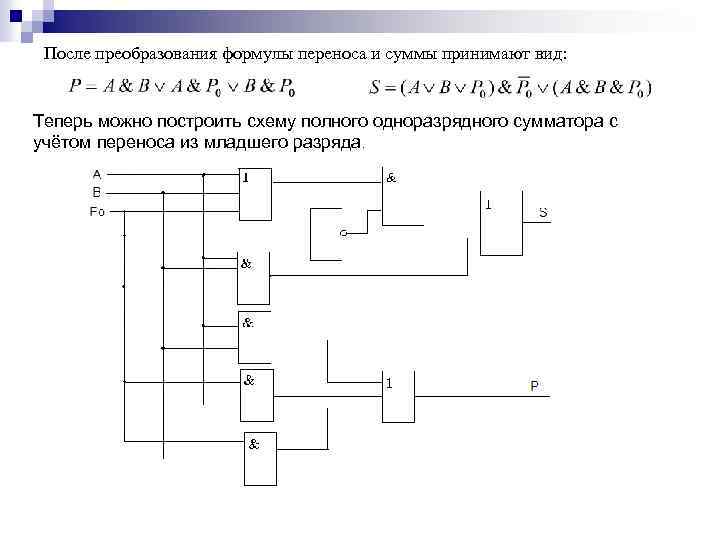 После преобразования формулы переноса и суммы принимают вид: Теперь можно построить схему полного одноразрядного сумматора с учётом переноса из младшего разряда.
После преобразования формулы переноса и суммы принимают вид: Теперь можно построить схему полного одноразрядного сумматора с учётом переноса из младшего разряда.
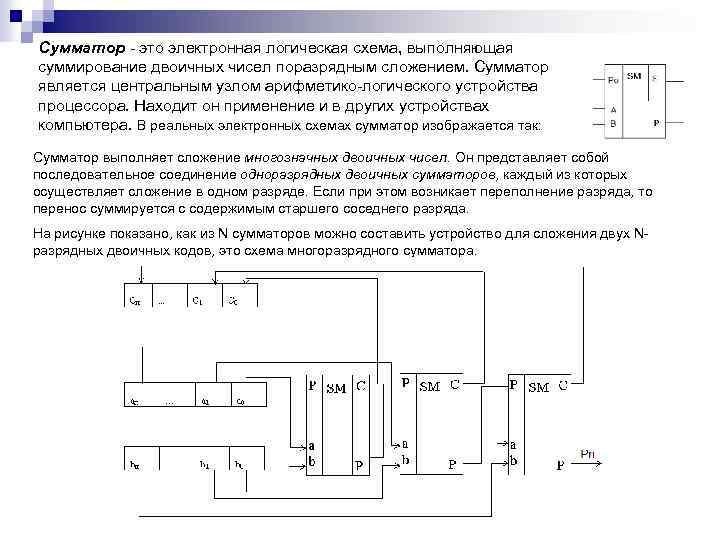 Сумматор это электронная логическая схема, выполняющая суммирование двоичных чисел поразрядным сложением. Сумматор является центральным узлом арифметико логического устройства процессора. Находит он применение и в других устройствах компьютера. В реальных электронных схемах сумматор изображается так: Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то перенос суммируется с содержимым старшего соседнего разряда. На рисунке показано, как из N сумматоров можно составить устройство для сложения двух N разрядных двоичных кодов, это схема многоразрядного сумматора.
Сумматор это электронная логическая схема, выполняющая суммирование двоичных чисел поразрядным сложением. Сумматор является центральным узлом арифметико логического устройства процессора. Находит он применение и в других устройствах компьютера. В реальных электронных схемах сумматор изображается так: Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то перенос суммируется с содержимым старшего соседнего разряда. На рисунке показано, как из N сумматоров можно составить устройство для сложения двух N разрядных двоичных кодов, это схема многоразрядного сумматора.
 ТРИГГЕР Триггер электронная схема, применяемая для хранения значения одноразрядного двоичного кода. Воздействуя на входы триггера, его переводят в одно из двух возможных состояний (0 или 1). С поступлением сигналов на входы триггера в зависимости от его состояния либо происходит переключение, либо исходное состояние сохраняется. При отсутствии входных сигналов триггер сохраняет свое состояние сколь угодно долго. Термин триггер происходит от английского слова trigger защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает "хлопанье". Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить ("перебрасываться") из одного электрического состояния в другое. Существуют разные варианты исполнения триггеров в зависимости от элементной базы (И НЕ, ИЛИ НЕ) и функциональных связей между сигналами на входах и выходах (RS, JK, T, D и другие). Самый распространённый тип триггера это RS триггер (S и R соответственно от английских set установка, и reset сброс). Условное обозначение RS триггера:
ТРИГГЕР Триггер электронная схема, применяемая для хранения значения одноразрядного двоичного кода. Воздействуя на входы триггера, его переводят в одно из двух возможных состояний (0 или 1). С поступлением сигналов на входы триггера в зависимости от его состояния либо происходит переключение, либо исходное состояние сохраняется. При отсутствии входных сигналов триггер сохраняет свое состояние сколь угодно долго. Термин триггер происходит от английского слова trigger защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает "хлопанье". Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить ("перебрасываться") из одного электрического состояния в другое. Существуют разные варианты исполнения триггеров в зависимости от элементной базы (И НЕ, ИЛИ НЕ) и функциональных связей между сигналами на входах и выходах (RS, JK, T, D и другие). Самый распространённый тип триггера это RS триггер (S и R соответственно от английских set установка, и reset сброс). Условное обозначение RS триггера:
 RS триггер построен на 2 х логических элементах: ИЛИ НЕ либо И – НЕ. Как, правило, триггер имеет 2 выхода: прямой и инверсный Q и Как он работает? Пусть на вход элемента № 1 подан сигнал 1, а на вход элемента № 3 0. На выходе элемента № 1 независимо от того, какой второй сигнал поступит на вход, будет 1, т. к. это элемент ИЛИ (по свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение 0 (Q=0). Следовательно, и на втором входе элемента № 3 установится сигнал 0. На выходе элемента № 3 0. Пройдя через элемент № 4 сигнал изменится на 1. Следовательно, = 1. Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0, =1. В момент прекращения входных сигналов (S=0, R=0) на выходе =1. Это напряжение подается на вход элемента № 1. На выходе элемента № 1 сохраняется 1, и на Q сигнал 0. На входах элемента № 3 0, следовательно =1. Таким образом, при отсутствии на внешних входах сигналов 1 триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить напряжение на выходах триггера, надо подать сигнал 1 на вход элемента № 3. Тогда Q=1, =0.
RS триггер построен на 2 х логических элементах: ИЛИ НЕ либо И – НЕ. Как, правило, триггер имеет 2 выхода: прямой и инверсный Q и Как он работает? Пусть на вход элемента № 1 подан сигнал 1, а на вход элемента № 3 0. На выходе элемента № 1 независимо от того, какой второй сигнал поступит на вход, будет 1, т. к. это элемент ИЛИ (по свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение 0 (Q=0). Следовательно, и на втором входе элемента № 3 установится сигнал 0. На выходе элемента № 3 0. Пройдя через элемент № 4 сигнал изменится на 1. Следовательно, = 1. Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0, =1. В момент прекращения входных сигналов (S=0, R=0) на выходе =1. Это напряжение подается на вход элемента № 1. На выходе элемента № 1 сохраняется 1, и на Q сигнал 0. На входах элемента № 3 0, следовательно =1. Таким образом, при отсутствии на внешних входах сигналов 1 триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить напряжение на выходах триггера, надо подать сигнал 1 на вход элемента № 3. Тогда Q=1, =0.
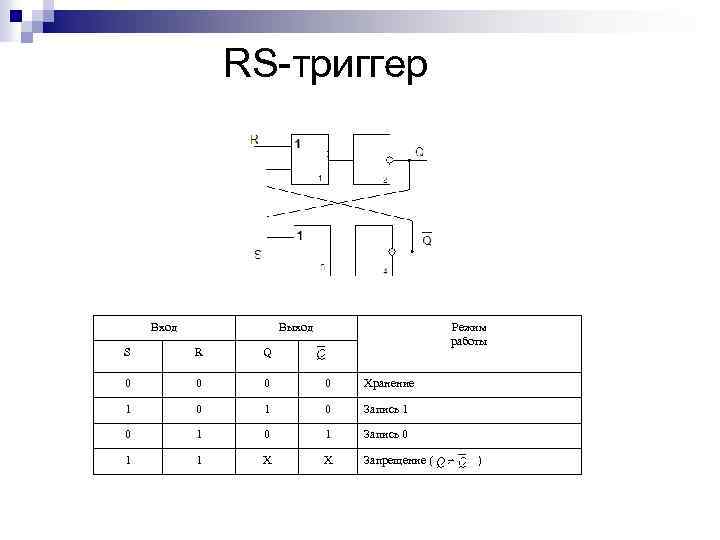 RS триггер Вход Выход Режим работы S R Q 0 0 Хранение 1 0 Запись 1 0 1 Запись 0 1 1 Х Х Запрещение ( )
RS триггер Вход Выход Режим работы S R Q 0 0 Хранение 1 0 Запись 1 0 1 Запись 0 1 1 Х Х Запрещение ( )
 РЕГИСТРЫ Функциональная схема компьютера, состоящая из триггеров, предназначенная для запоминания многоразрядных кодов и выполнения над ними некоторых логических преобразований называется регистром. Упрощенно регистр можно представить как совокупность ячеек, в каждой из которых может быть записано одно из двух значений: 0 или 1, то есть один разряд двоичного числа. С помощью регистров можно выполнять следующие операции: установку, сдвиг, преобразование. Основными типами регистров являются параллельные и последовательные (сдвигающие). Совокупность регистров, используемых ЭВМ для запоминания программы работы, исходных и промежуточных результатов называется оперативной памятью (ОП). Регистры содержатся в различных вычислительных узлах компьютера процессоре, периферийных устройствах и т. д. Регистр это устройство, предназначенное для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.
РЕГИСТРЫ Функциональная схема компьютера, состоящая из триггеров, предназначенная для запоминания многоразрядных кодов и выполнения над ними некоторых логических преобразований называется регистром. Упрощенно регистр можно представить как совокупность ячеек, в каждой из которых может быть записано одно из двух значений: 0 или 1, то есть один разряд двоичного числа. С помощью регистров можно выполнять следующие операции: установку, сдвиг, преобразование. Основными типами регистров являются параллельные и последовательные (сдвигающие). Совокупность регистров, используемых ЭВМ для запоминания программы работы, исходных и промежуточных результатов называется оперативной памятью (ОП). Регистры содержатся в различных вычислительных узлах компьютера процессоре, периферийных устройствах и т. д. Регистр это устройство, предназначенное для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.
 РЕГИСТРЫ Существует несколько типов регистров, отличающихся видом выполняемых операций. Некоторые важные регистры имеют свои названия, например: сдвиговый регистр предназначен для выполнения операции сдвига; счетчики схемы, способные считать поступающие на вход импульсы. К ним относятся Т триггеры (название от англ. tumble опрокидываться). Этот триггер имеет один счетный вход и два выхода. Под действием сигналов триггер меняет свое состояние с нулевого на единичное и наоборот. Число перебрасываний соответствует числу поступивших сигналов; счетчик команд регистр устройства управления процессора (УУ), содержимое которого соответствует адресу очередной выполняемой команды; служит для автоматической выборки программы из последовательных ячеек памяти; регистр команд регистр УУ для хранения кода команды на период времени, необходимый для ее выполнения. Часть его разрядов используется для хранения кода операции, остальные для хранения кодов адресов операндов. В ЭВМ применяются регистры 8, 16, 32, 48 и 64 разрядов.
РЕГИСТРЫ Существует несколько типов регистров, отличающихся видом выполняемых операций. Некоторые важные регистры имеют свои названия, например: сдвиговый регистр предназначен для выполнения операции сдвига; счетчики схемы, способные считать поступающие на вход импульсы. К ним относятся Т триггеры (название от англ. tumble опрокидываться). Этот триггер имеет один счетный вход и два выхода. Под действием сигналов триггер меняет свое состояние с нулевого на единичное и наоборот. Число перебрасываний соответствует числу поступивших сигналов; счетчик команд регистр устройства управления процессора (УУ), содержимое которого соответствует адресу очередной выполняемой команды; служит для автоматической выборки программы из последовательных ячеек памяти; регистр команд регистр УУ для хранения кода команды на период времени, необходимый для ее выполнения. Часть его разрядов используется для хранения кода операции, остальные для хранения кодов адресов операндов. В ЭВМ применяются регистры 8, 16, 32, 48 и 64 разрядов.
 ШИФРАТОРЫ И ДЕШИФРАТОРЫ Шифратор и дешифратор являются типовыми узлами ЭВМ. Шифратор (кодер) это логическое устройство, которое преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (например в клавиатуре), для преобразования десятичных чисел в двоичную систему счисления. Дешифратор (декодер) это логическое устройство, преобразующее двоичный код, поступающий на его входы, в сигнал только на одном из его выходов. Дешифраторы широко применяются в устройствах управления, в системах цифровой индикации с газоразрядными индикаторами, для построения распределителей импульсов по различным цепям и т. д. Схема используется для перевода двоичных цифр в десятичные. Дешифратор двоичного n разрядного кода имеет 2 n выходов, т. к. каждому из 2 n значений входного кода должен соответствовать единичный сигнал на одном из выходов дешифратора.
ШИФРАТОРЫ И ДЕШИФРАТОРЫ Шифратор и дешифратор являются типовыми узлами ЭВМ. Шифратор (кодер) это логическое устройство, которое преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (например в клавиатуре), для преобразования десятичных чисел в двоичную систему счисления. Дешифратор (декодер) это логическое устройство, преобразующее двоичный код, поступающий на его входы, в сигнал только на одном из его выходов. Дешифраторы широко применяются в устройствах управления, в системах цифровой индикации с газоразрядными индикаторами, для построения распределителей импульсов по различным цепям и т. д. Схема используется для перевода двоичных цифр в десятичные. Дешифратор двоичного n разрядного кода имеет 2 n выходов, т. к. каждому из 2 n значений входного кода должен соответствовать единичный сигнал на одном из выходов дешифратора.
 Тема 4 Вычислительная техника
Тема 4 Вычислительная техника
 «Computer» это вычислитель Само слово компьютер является производным от английских слов to compute, computer, которые переводятся как «вычислять» , «вычислитель» (английское слово, в свою очередь, происходит от латинского computo — «вычисляю» ). Впервые трактовка слова компьютер появилась в 1897 году в Оксфордском английском словаре. Его составители тогда понимали компьютер как механическое вычислительное устройство. На заре эры компьютеров считалось, что основная функция компьютера — вычисление. Однако в настоящее время полагают, что основная их функция — управление.
«Computer» это вычислитель Само слово компьютер является производным от английских слов to compute, computer, которые переводятся как «вычислять» , «вычислитель» (английское слово, в свою очередь, происходит от латинского computo — «вычисляю» ). Впервые трактовка слова компьютер появилась в 1897 году в Оксфордском английском словаре. Его составители тогда понимали компьютер как механическое вычислительное устройство. На заре эры компьютеров считалось, что основная функция компьютера — вычисление. Однако в настоящее время полагают, что основная их функция — управление.
 Принципы фон Неймана Схема устройства компьютера впервые была предложена в 1946 году американским ученым Джоном фон Нейманом. Дж. фон Нейман сформулировал основные принципы работы ЭВМ, которые во многом сохранились и в современных компьютерах.
Принципы фон Неймана Схема устройства компьютера впервые была предложена в 1946 году американским ученым Джоном фон Нейманом. Дж. фон Нейман сформулировал основные принципы работы ЭВМ, которые во многом сохранились и в современных компьютерах.
 Принципы фон Неймана: 1. 2. 3. Принцип программного управления. Программа состоит из набора команд, которые выполняются процессором автоматически друг за другом в определённой последовательности. Принцип адресности. Основная память состоит из перенумерованных ячеек; процессору времени доступна любая ячейка. Наиболее оптимальным оказываются 8 битные ячейки. Принцип однородности памяти. Программы и данные хранятся в одной и той же памяти. Поэтому компьютер не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.
Принципы фон Неймана: 1. 2. 3. Принцип программного управления. Программа состоит из набора команд, которые выполняются процессором автоматически друг за другом в определённой последовательности. Принцип адресности. Основная память состоит из перенумерованных ячеек; процессору времени доступна любая ячейка. Наиболее оптимальным оказываются 8 битные ячейки. Принцип однородности памяти. Программы и данные хранятся в одной и той же памяти. Поэтому компьютер не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.
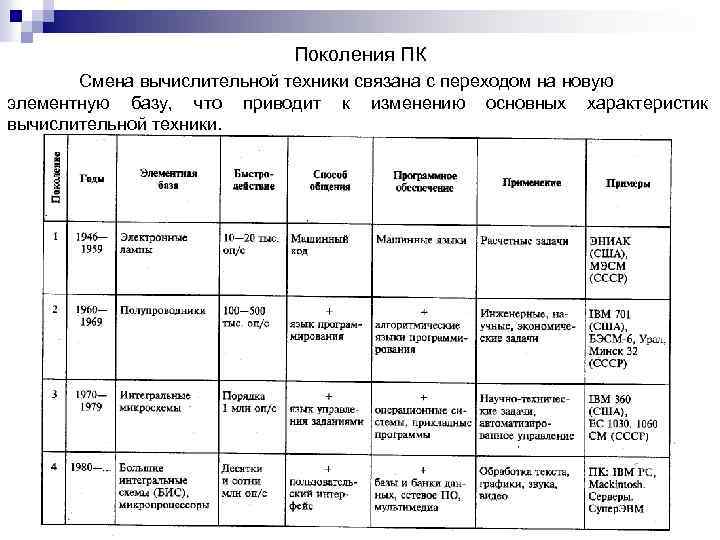 Поколения ПК Смена вычислительной техники связана с переходом на новую элементную базу, что приводит к изменению основных характеристик вычислительной техники.
Поколения ПК Смена вычислительной техники связана с переходом на новую элементную базу, что приводит к изменению основных характеристик вычислительной техники.
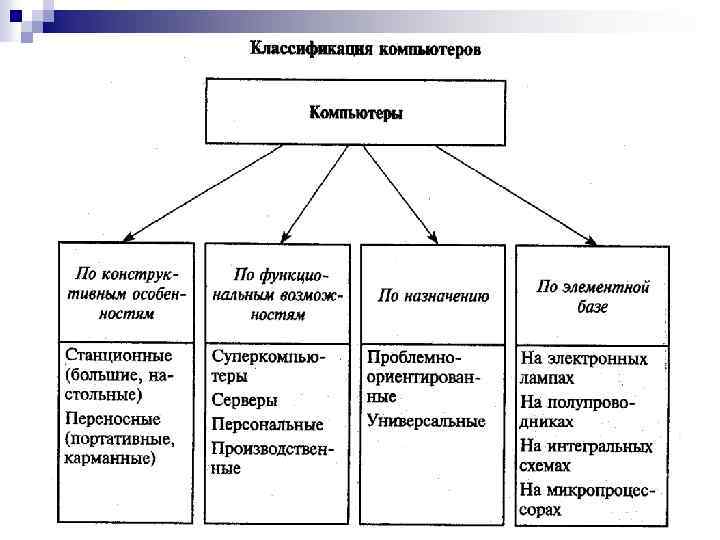
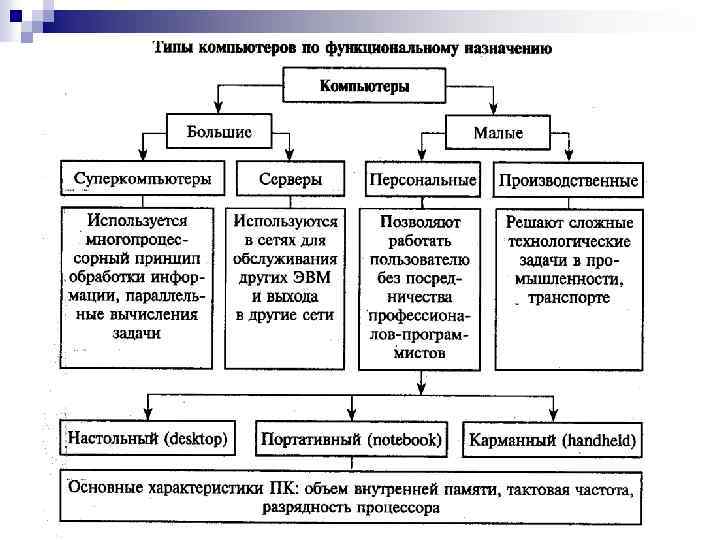
 Архитектура ЭВМ Описание устройства и принципов работы компьютера, достаточное для пользователя и программиста называют архитектурой ЭВМ. Архитектура не включает в себя конструктивных подробностей устройства машины, электронных схем. Эти сведения нужны конструкторам, специалистам по наладке и ремонту ЭВМ. К архитектуре относится именно логическое построение вычислительных средств, без учета конкретных деталей их реализации.
Архитектура ЭВМ Описание устройства и принципов работы компьютера, достаточное для пользователя и программиста называют архитектурой ЭВМ. Архитектура не включает в себя конструктивных подробностей устройства машины, электронных схем. Эти сведения нужны конструкторам, специалистам по наладке и ремонту ЭВМ. К архитектуре относится именно логическое построение вычислительных средств, без учета конкретных деталей их реализации.
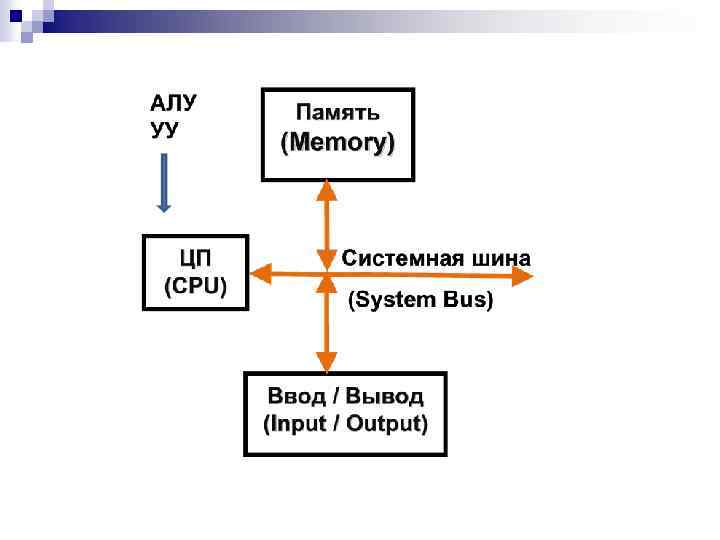
 Магистрально-модульный принцип положен в основу построения архитектуры компьютера четвертого поколения и заключается в том, что информационная связь между устройствами осуществляется через общую магистраль (системную магистраль). Магистрально модульный принцип позволяет производить необходимую модернизацию компьютера, замену блоков с минимальными затратами труда и времени. Системная магистраль является основным узлом компьютера, связывающим микропроцессор и оперативную память с периферийными устройствами в единое целое. В состав системной магистрали входят. набор электронных проводов, связывающих центральный процессор и внутреннюю память с периферийными устройствами для передачи данных (шина данных), служебных сигналов (шина управления) и адресов памяти (шина адреса); регистры, в которых запоминается передаваемая информация; микросхемы северного моста (мост памяти) и южного моста (мост ввода вывода). Набор электронных проводников делится на шины данных, адреса и управления. Шина – это физическая совокупность проводов, предназначенная для передачи различных сигналов.
Магистрально-модульный принцип положен в основу построения архитектуры компьютера четвертого поколения и заключается в том, что информационная связь между устройствами осуществляется через общую магистраль (системную магистраль). Магистрально модульный принцип позволяет производить необходимую модернизацию компьютера, замену блоков с минимальными затратами труда и времени. Системная магистраль является основным узлом компьютера, связывающим микропроцессор и оперативную память с периферийными устройствами в единое целое. В состав системной магистрали входят. набор электронных проводов, связывающих центральный процессор и внутреннюю память с периферийными устройствами для передачи данных (шина данных), служебных сигналов (шина управления) и адресов памяти (шина адреса); регистры, в которых запоминается передаваемая информация; микросхемы северного моста (мост памяти) и южного моста (мост ввода вывода). Набор электронных проводников делится на шины данных, адреса и управления. Шина – это физическая совокупность проводов, предназначенная для передачи различных сигналов.
 Центральный процессор – это основной компонент компьютера, который выполняет арифметические и логические операции, заданные программой, управляет вычислительным процессом и координирует работу периферийных устройств компьютера через контроллеры. Центральный процессор содержит: АЛУ – арифметико логическое устройство, которое выполняет арифметические и логические операции над двоичными кодами; УУ – устройство управления, которое с помощью управляющих сигналов обеспечивает взаимодействие всех компонентов компьютера; ПП – процессорную память, реализованную с помощью регистров и предназначенную для временного запоминания двоичных кодов. Микропроцессор – микросхема (сверхбольшая интегральная схема, содержащая несколько миллионов компонентов), реализующая функции центрального процессора. Северный мост (мост памяти) – микросхема системной магистрали, предназначенная для обмена информацией микропроцессора с быстродействующими устройствами (оперативной памятью, видеоадаптером). Этапы обработки команд процессором: 1. выборка команды из ОП; 2. декодирование; 3. расшифровка; 4. выполнение; 5. запись результата в ОП.
Центральный процессор – это основной компонент компьютера, который выполняет арифметические и логические операции, заданные программой, управляет вычислительным процессом и координирует работу периферийных устройств компьютера через контроллеры. Центральный процессор содержит: АЛУ – арифметико логическое устройство, которое выполняет арифметические и логические операции над двоичными кодами; УУ – устройство управления, которое с помощью управляющих сигналов обеспечивает взаимодействие всех компонентов компьютера; ПП – процессорную память, реализованную с помощью регистров и предназначенную для временного запоминания двоичных кодов. Микропроцессор – микросхема (сверхбольшая интегральная схема, содержащая несколько миллионов компонентов), реализующая функции центрального процессора. Северный мост (мост памяти) – микросхема системной магистрали, предназначенная для обмена информацией микропроцессора с быстродействующими устройствами (оперативной памятью, видеоадаптером). Этапы обработки команд процессором: 1. выборка команды из ОП; 2. декодирование; 3. расшифровка; 4. выполнение; 5. запись результата в ОП.
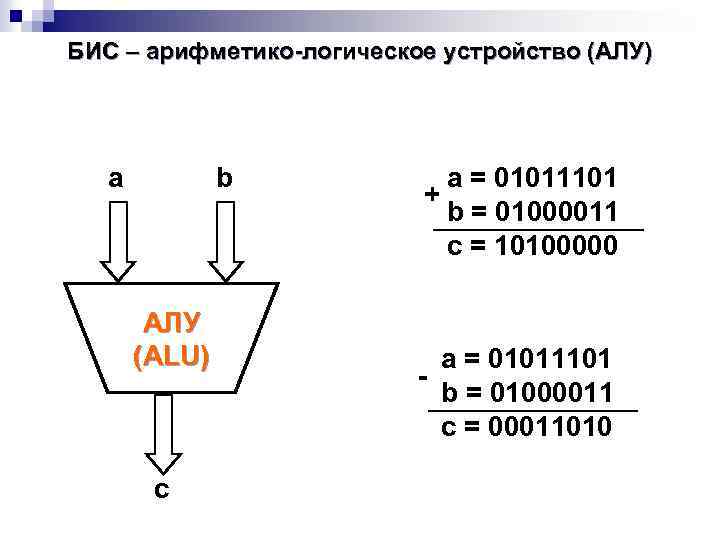 БИС – арифметико-логическое устройство (АЛУ) a b АЛУ (ALU) c a = 01011101 + b = 01000011 c = 10100000 a = 01011101 b = 01000011 c = 00011010
БИС – арифметико-логическое устройство (АЛУ) a b АЛУ (ALU) c a = 01011101 + b = 01000011 c = 10100000 a = 01011101 b = 01000011 c = 00011010
 Характеристики ЦП: Тактовая частота – количество тактов в секунду. Такт – интервал времени между двумя последовательными импульсами электрического тока, в течение которого выполняется элементарная операция, например пересылка двоичного кода из ЦП в ОП. Измеряется в герцах (1 ГГц = 1 млрд тактов в секунду). Производительность – количество операций в секунду, которая определяется: скоростью работы процессора, пропускной способностью шины данных и скоростью обмена с внешними устройствами. Разрядность процессора – число одновременно обрабатываемых бит. Процессоры могут быть 8 , 16 , 32 , 64 , 128 разрядные. Интерфейс с системной шиной определяет совпадение разрядности ЦП и внешней шины. Объем физически адресуемой основной памяти определяется разрядностью адресной шины. Если N – разрядность шины, то 2 N – количество двоичных кодов, которые по ней можно передать, а значит, количество ячеек основной памяти, к которым, используя адресную шину, может обратиться ЦП. Южный мост (мост ввода вывода) – микросхема системной магистрали, предназначенная для обмена информацией микропроцессора с медленными устройствами (периферийными устройствами, постоянной памятью компьютера).
Характеристики ЦП: Тактовая частота – количество тактов в секунду. Такт – интервал времени между двумя последовательными импульсами электрического тока, в течение которого выполняется элементарная операция, например пересылка двоичного кода из ЦП в ОП. Измеряется в герцах (1 ГГц = 1 млрд тактов в секунду). Производительность – количество операций в секунду, которая определяется: скоростью работы процессора, пропускной способностью шины данных и скоростью обмена с внешними устройствами. Разрядность процессора – число одновременно обрабатываемых бит. Процессоры могут быть 8 , 16 , 32 , 64 , 128 разрядные. Интерфейс с системной шиной определяет совпадение разрядности ЦП и внешней шины. Объем физически адресуемой основной памяти определяется разрядностью адресной шины. Если N – разрядность шины, то 2 N – количество двоичных кодов, которые по ней можно передать, а значит, количество ячеек основной памяти, к которым, используя адресную шину, может обратиться ЦП. Южный мост (мост ввода вывода) – микросхема системной магистрали, предназначенная для обмена информацией микропроцессора с медленными устройствами (периферийными устройствами, постоянной памятью компьютера).
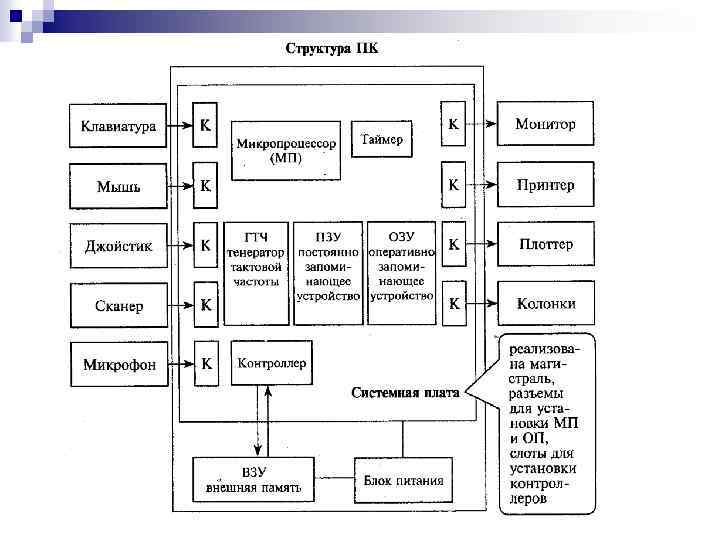
 Слот – разъем на системной плате компьютера, в который устанавливаются платы контроллеров устройств (например, видеоадаптер) и дополнительных устройств (например, модем). Контроллеры – устанавливаются в слоты расширения системной платы и управляют работой внешних устройств. Видеоадаптер (видеокарта) – электронная плата, которая обрабатывает видеоданные и управляет выводом изображения на экран монитора. Порт – специальный разъем, расположенный на тыльной стороне системного блока для подключения внешних устройств и имеющий собственное адресное пространство. Параллельный порт – используется для подсоединения внешних устройств, которым необходимо передавать большой объем информации на близкое расстояние (8 бит по 8 проводам одновременно) – принтер, сканер; LPT 1; LPT 2; LPT 3. Последовательный порт – используется для подключения к системному блоку манипуляторов, модемов и др. устройств, передача информации на большие расстояния (передается последовательный поток данных по 1 биту) – коммуникационный; СОМ 1 COM 4. Порт USB (универсальная последовательная шина), который обеспечивает высокоскоростное подключение к компьютеру периферийных устройств (сканеры, цифровые камеры).
Слот – разъем на системной плате компьютера, в который устанавливаются платы контроллеров устройств (например, видеоадаптер) и дополнительных устройств (например, модем). Контроллеры – устанавливаются в слоты расширения системной платы и управляют работой внешних устройств. Видеоадаптер (видеокарта) – электронная плата, которая обрабатывает видеоданные и управляет выводом изображения на экран монитора. Порт – специальный разъем, расположенный на тыльной стороне системного блока для подключения внешних устройств и имеющий собственное адресное пространство. Параллельный порт – используется для подсоединения внешних устройств, которым необходимо передавать большой объем информации на близкое расстояние (8 бит по 8 проводам одновременно) – принтер, сканер; LPT 1; LPT 2; LPT 3. Последовательный порт – используется для подключения к системному блоку манипуляторов, модемов и др. устройств, передача информации на большие расстояния (передается последовательный поток данных по 1 биту) – коммуникационный; СОМ 1 COM 4. Порт USB (универсальная последовательная шина), который обеспечивает высокоскоростное подключение к компьютеру периферийных устройств (сканеры, цифровые камеры).
 Пути повышения производительности ЭВМ совершенствование элементной базы; Ø многопроцессорная (многоядерная) архитектура; Ø многоуровневая память (кэшпамять). Ø
Пути повышения производительности ЭВМ совершенствование элементной базы; Ø многопроцессорная (многоядерная) архитектура; Ø многоуровневая память (кэшпамять). Ø
 СБИС Teraflops Research Chip Все 80 ядер полностью идентичны. Роутер ядра используется для передачи данных и команд в сети между ядрами он имеет пять 39 -битных портов. Общая пропускную способность 80 ГБ/с (при работе на частоте 4 ГГц).
СБИС Teraflops Research Chip Все 80 ядер полностью идентичны. Роутер ядра используется для передачи данных и команд в сети между ядрами он имеет пять 39 -битных портов. Общая пропускную способность 80 ГБ/с (при работе на частоте 4 ГГц).
 Тема 5 Программное обеспечение компьютеров
Тема 5 Программное обеспечение компьютеров
 Software ПК = Hardware + Software (ПО): Системное ПО - управление компьютером. Прикладное ПО – решение конкретных задач.
Software ПК = Hardware + Software (ПО): Системное ПО - управление компьютером. Прикладное ПО – решение конкретных задач.
 Системное ПО 1. Операционные системы (ОС) – планирование (ОС) вычислительного процесса и распоряжение ресурсами машины ( DOS, Unix, Windows, Linux, OS/2 ). DOS – однозадачная ОС. 2. Файловые оболочки – для диалога пользователя с ОС оболочки (Командная строка, Norton Commander, Far) 3. Драйверы – для связи между ОС и внешними устройствами Драйверы (драйверы мыши, клавиатуры, принтера и т. д. ). копирование, отладчики программ (debuger), трансляторы и т. д.
Системное ПО 1. Операционные системы (ОС) – планирование (ОС) вычислительного процесса и распоряжение ресурсами машины ( DOS, Unix, Windows, Linux, OS/2 ). DOS – однозадачная ОС. 2. Файловые оболочки – для диалога пользователя с ОС оболочки (Командная строка, Norton Commander, Far) 3. Драйверы – для связи между ОС и внешними устройствами Драйверы (драйверы мыши, клавиатуры, принтера и т. д. ). копирование, отладчики программ (debuger), трансляторы и т. д.
 Прикладное ПО n n n Текстовые редакторы (me, Лексикон) – позволяют создавать документы и редактировать их; Текстовые процессоры (Word, Writer) – дают возможность форматировать (оформлять) документы, добавлять в них графику, таблицы, формулы, фрагменты документов из других пакетов программ; Графические редакторы (Corel. Draw, Photoshop, Paint);
Прикладное ПО n n n Текстовые редакторы (me, Лексикон) – позволяют создавать документы и редактировать их; Текстовые процессоры (Word, Writer) – дают возможность форматировать (оформлять) документы, добавлять в них графику, таблицы, формулы, фрагменты документов из других пакетов программ; Графические редакторы (Corel. Draw, Photoshop, Paint);
 Прикладное ПО n Табличные процессоры (Excel, Calc, Lotus) – позволяют хранить и обрабатывать огромные массивы информации в виде двумерных таблиц. Имеют большие вычислительные и графические возможности; n Системы управления базами данных – СУБД (Fox. Pro, Access, DBase) – для создания баз данных. Имеют хорошие возможности поиска информации;
Прикладное ПО n Табличные процессоры (Excel, Calc, Lotus) – позволяют хранить и обрабатывать огромные массивы информации в виде двумерных таблиц. Имеют большие вычислительные и графические возможности; n Системы управления базами данных – СУБД (Fox. Pro, Access, DBase) – для создания баз данных. Имеют хорошие возможности поиска информации;
 Прикладное ПО Экспертные системы – для принятия решений в различных областях; n Программы пользователей. n
Прикладное ПО Экспертные системы – для принятия решений в различных областях; n Программы пользователей. n
 Стандартное ПО Это программы, устанавливаемые вместе с операционной системой: n Калькулятор n Блокнот n Paint n Игры n и т. д.
Стандартное ПО Это программы, устанавливаемые вместе с операционной системой: n Калькулятор n Блокнот n Paint n Игры n и т. д.
 Языки программирования – основные понятия n АЛГОРИТМ – последовательность действий. Языки программирования служат для реализации алгоритмов на ЭВМ. n МАШИННЫЙ КОД – последовательность команд для ЭВМ (двоичных чисел). Процессоры ЭВМ работают с машинным кодом.
Языки программирования – основные понятия n АЛГОРИТМ – последовательность действий. Языки программирования служат для реализации алгоритмов на ЭВМ. n МАШИННЫЙ КОД – последовательность команд для ЭВМ (двоичных чисел). Процессоры ЭВМ работают с машинным кодом.
 Языки программирования Алгоритмические языки – искусственные языки, содержащие ограниченный набор слов (команд) и очень жесткие правила их записи. Создано более 500 языков программирования. Из них около 30 – универсальные (можно написать программу для любой области): Алгол, Фортран, Паскаль, Си, Бейсик и т. д. Остальные языки специальные: Про. Лог –программирование логических задач; Электро расчет электронных схем и т. д.
Языки программирования Алгоритмические языки – искусственные языки, содержащие ограниченный набор слов (команд) и очень жесткие правила их записи. Создано более 500 языков программирования. Из них около 30 – универсальные (можно написать программу для любой области): Алгол, Фортран, Паскаль, Си, Бейсик и т. д. Остальные языки специальные: Про. Лог –программирование логических задач; Электро расчет электронных схем и т. д.
 Уровни языков программирования Язык программирования, ориентированный на конкретный процессор, называется языком программирования низкого уровня (Ассемблер ASM-86 - ориентирован на процессор Intel).
Уровни языков программирования Язык программирования, ориентированный на конкретный процессор, называется языком программирования низкого уровня (Ассемблер ASM-86 - ориентирован на процессор Intel).
 Языки программирования высокого уровня Язык программирования, не зависящий от типа процессора, называется языком программирования высокого уровня: Паскаль (Pascal, Object Pascal DELPHI); n Бейсик (Basic, Visual Basic for Applications, Visual Basic Script); n Си (С, С++, Visual C) и т. д. n
Языки программирования высокого уровня Язык программирования, не зависящий от типа процессора, называется языком программирования высокого уровня: Паскаль (Pascal, Object Pascal DELPHI); n Бейсик (Basic, Visual Basic for Applications, Visual Basic Script); n Си (С, С++, Visual C) и т. д. n
 Компиляторы и интерпретаторы Это программы-переводчики с алгоритмического языка в машинный код n Интерпретатор поочередно переводит в машинный код и исполняет каждый оператор программы. n Компилятор переводит в машинный код всю программу и создает новый файл с расширением exe.
Компиляторы и интерпретаторы Это программы-переводчики с алгоритмического языка в машинный код n Интерпретатор поочередно переводит в машинный код и исполняет каждый оператор программы. n Компилятор переводит в машинный код всю программу и создает новый файл с расширением exe.
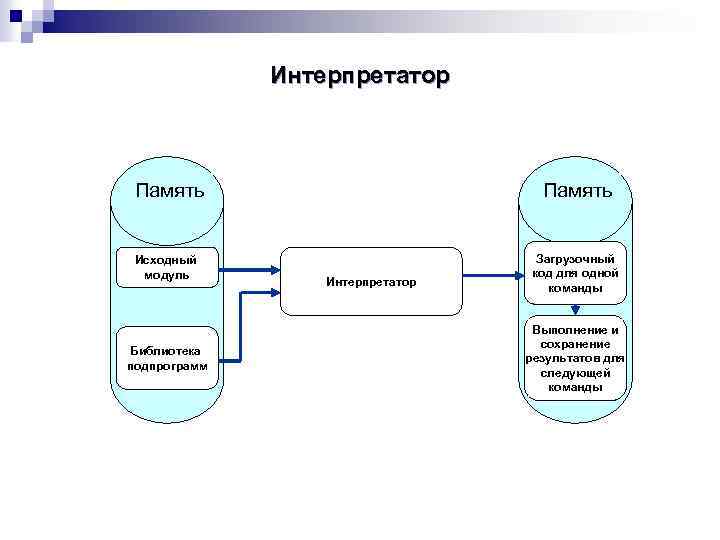 Интерпретатор Память Исходный модуль Библиотека подпрограмм Память Интерпретатор Загрузочный код для одной команды Выполнение и сохранение результатов для следующей команды
Интерпретатор Память Исходный модуль Библиотека подпрограмм Память Интерпретатор Загрузочный код для одной команды Выполнение и сохранение результатов для следующей команды
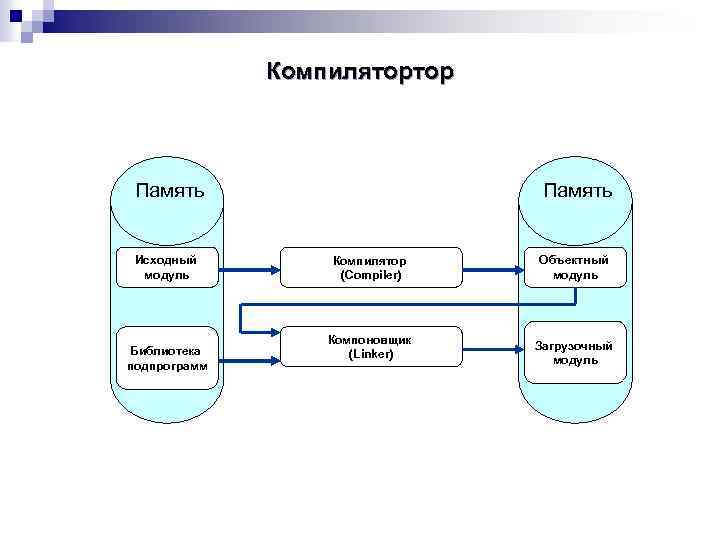 Компилятортор Память Исходный модуль Библиотека подпрограмм Память Компилятор (Compiler) Объектный модуль Компоновщик (Linker) Загрузочный модуль
Компилятортор Память Исходный модуль Библиотека подпрограмм Память Компилятор (Compiler) Объектный модуль Компоновщик (Linker) Загрузочный модуль


