Информатика и математика 1 семестр – 24/16 –

Информатика и математика 1 семестр – 24/16 – зачет 2 семестр – 36/32 – экзамен Ведущая кафедра: компьютерных технологий и систем доцент Креймер Алексей Семенович

Лекция 1 Предмет "Математика и информатика". Элементы теории множеств

Вопросы 1. Математика и информатика 2. Понятие множества. Виды множеств. 3. 4. 5. 6. Специальные виды множеств Взаимно-однозначное соответствие. Мощность множества Операции над множествами Свойства операций над множествами. Мощность объединения множеств

Математика и информатика Основная цель курса – изучить фундаментальные теоретические и практические основы информатики и научиться их применять в своей профессиональной деятельности. Математика при этом выступает в роли "базиса", основы для информатики, являясь также инструментом развития логического и абстрактного мышления.

Учение о множествах Кантора До второй половины XIX века понятие «множества» не рассматривалось в качестве математического ( «множество книг на полке» , «множество человеческих добродетелей» и т. д. — всё это чисто бытовые обороты речи). Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным «множеством» .

Парадоксы теории множеств Учение о множествах, предложенное Георгом Кантором еще называют "наивной теорией множеств", т. к. в нем запрещаются действия, ведущие к парадоксам. В одной стране вышел указ: «Мэры всех городов должны жить не в своем городе, а в специальном Городе мэров» Где должен жить мэр Города мэров?

Понятие множества является одним из ключевых понятий математики. Строгого определения этого понятие не существует (как, например, информации, числа и др. ). Множество – совокупность элементов, объединенных по какому-либо признаку. Пример. Множество студентов Куб. ГАУ, множество деревьев в дендрарии, множество стульев в аудитории.

Определения Множество состоит из элементов, при этом нет никакой разницы, каким именно образом расположены эти элементы внутри множества. Имеет значение лишь факт принадлежности элемента множеству. Будем обозначать множества латинскими буквами: A, B, C и т. д. Факт принадлежности элемента множеству обозначим следующим образом: a A.

Виды множеств Можно выделить следующие виды множеств: конечные и бесконечные. В конечном множестве число элементов ограничено, конечно. Пример: множество законов РФ. В бесконечном множестве, напротив, число элементов бесконечно. Пример: множество целых чисел.

К понятию бесконечности Необходимо уточнение понятия бесконечности. Существует два вида бесконечности: потенциальная (геометрическая интерпретация – прямая, продолжающаяся бесконечно в обе стороны) и актуальная (число точек в отрезке прямой).

Специальные виды множеств К специальным видам множеств относятся пустое множество и универсальное множество (универсум). Пустое множество не содержит ни одного элемента, обозначается символом . Универсум содержит все мыслимые элементы, обозначается символом U. Пример пустого множества: множество студентов 10 курса Куб. ГАУ.

Понятие мощности множества «Мощность» представляет собой некую количественную характеристику множества. Мощность множества можно определить как характеристику двух эквивалентных множеств.

Эквивалентные и равные множества Эквивалентными называются такие множества, между элементами которых можно установить взаимно-однозначное соответствие, т. е элементу аi множества А соответствует только один элемент bj множества B и наоборот. В отличие от эквивалентных равные множества просто содержат одинаковые элементы.

Примеры Пример. А={1, 2, 3}, B={1, 2, 3}, C={a, b, c} Множества А и В равны, множества А, В и С эквивалентны. Таким образом мощность это общая характеристика разных множеств – например, множество пальцев на одной руке и множество пяти коров на лугу связывает только одно – одинаковая мощность.

Операции над множествами Объединением множеств А и В называется такое множество С, которое содержит все элементы множеств А и В. Пример. А={1, 2, 3, 4} B={2, 3, 5, 7, 0} C = A B = {0, 1, 2, 3, 4, 5, 7}

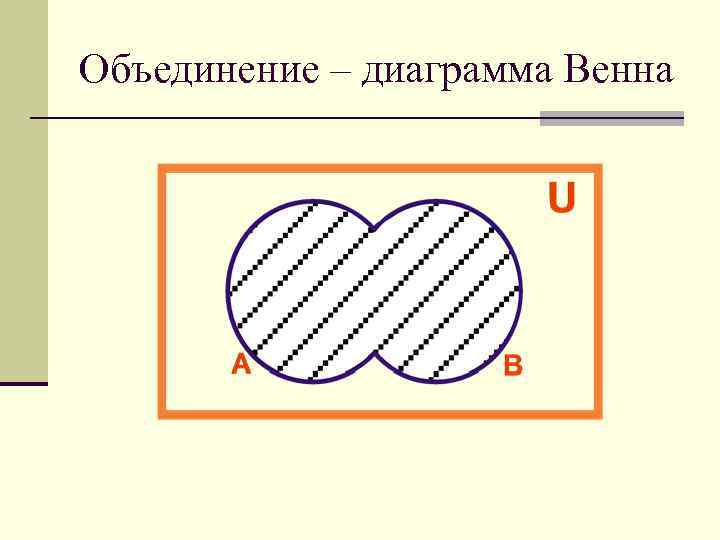Объединение – диаграмма Венна

Пересечением множеств А и В называется такое множество С, которое содержит только элементы, принадлежащие одновременно А и В. Пример. А={1, 2, 3, 4} B={2, 3, 5, 7, 0} C = A B = {2, 3}

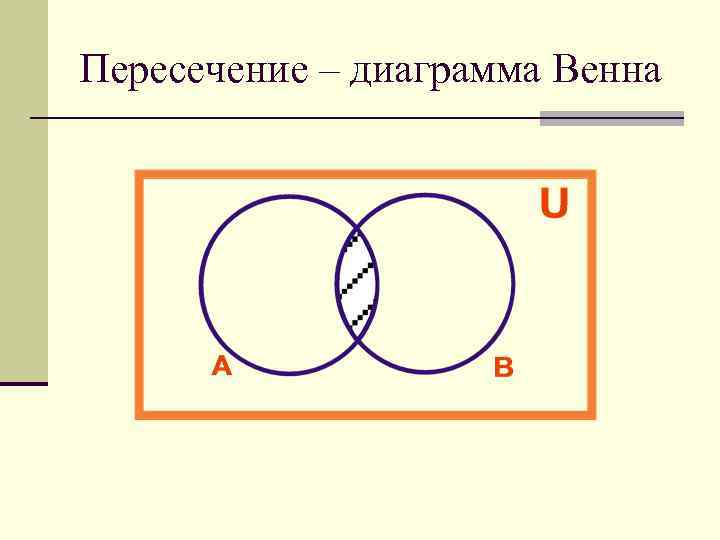Пересечение – диаграмма Венна

Дополнением множества А называется такое множество С, в которое входят все элементы, не принадлежащие множеству А.

Разностью множеств В и А называют множество С, которое состоит из элементов множества В, не принадлежащих множеству А. Пример. А={1, 2, 3, 4} B={2, 3, 5, 7, 0} С = ВА = {5, 7, 0}

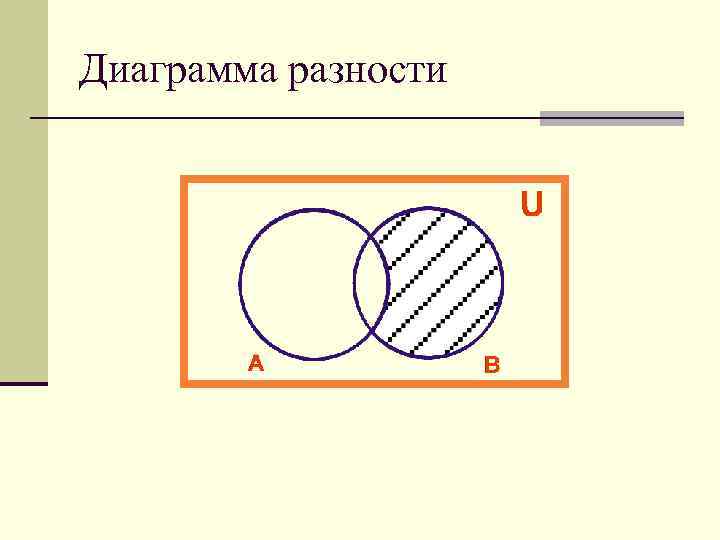Диаграмма разности

Свойства операций над множествами Свойства коммутативности. Коммутативность объединения множеств A B B A Коммутативность пересечения множеств: A B B A

Свойства операций над множествами Свойства ассоциативности Ассоциативность объединения множеств A (B C) (A B) C Ассоциативность пересечения множеств A (B C) (A B) C

Свойства операций над множествами Свойства дистрибутивности Дистрибутивность пересечения относительно объединения A (B C) (A B) (A C) Дистрибутивность объединения относительно пересечения A (B C) (A B) (A C)

Свойства операций над множествами Свойства универсального множества A U U A U A Ā U A Свойства пустого множества A А A Ā А

Мощность объединения множеств |А В| = |A| + |B| –|А ∩ В| |А В С| = |A| + |B| + |С| – – |А ∩ В| – |А ∩ С| – |В ∩ С| – + |A + B + С|