ИНФОРМАТИКА 1 Рекомендуемая литература 1 Волков В

ИНФОРМАТИКА 1

Рекомендуемая литература 1. Волков В. Б. , Макарова Н. В. Информатика – СПб. : Питер, 2011. 2. Макарова Н. В. Практикум по информатике – СПб. : Питер, 2012. 3. Хеннер Е. К. , Могилев А. В. , Пак Н. И. Информатика – М. : Academia, 2012. 4. Симонович С. В. Информатика. Базовый курс – СПб. : Питер, 2012. 5. Справочная система программных продуктов. 2

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАТИКИ 3

Разделы: 1. Процессы сбора, передачи и обработки информации 2. Атрибутивные свойства информации. 3. Системы счисления 4. Меры и единицы количества и объема информации 5. Кодирование данных в ЭВМ 4

Разделы: 6. Основные понятия алгебры логики 7. Логические основы ЭВМ. 5

1. Процессы сбора, передачи и обработки информации Информатика Термин «информатика» (комбинация из слов «информация» и «автоматика» ) был введен в 1970 -х годах прошлого века в связи с началом массового производства и широкого внедрения электронных вычислительных машин (ЭВМ). Информатика — это наука, предметом изучения которой являются процессы сбора, получения, передачи, хранения, накопления, отображения, использования, защиты, преобразования и обработки информации. Основные направления развития информатики можно подразделить на теоретическую и прикладную информатику. 6

Теоретическая информатика включает теорию информации, информационное моделирование, методы измерения информации, алгебру логики, теорию алгоритмов, искусственный интеллект, теорию автоматов, теорию баз данных и представление знаний. Прикладная информатика включает вычислительные и информационные технологии, а также техническое и программное обеспечение информационных процессов. 7

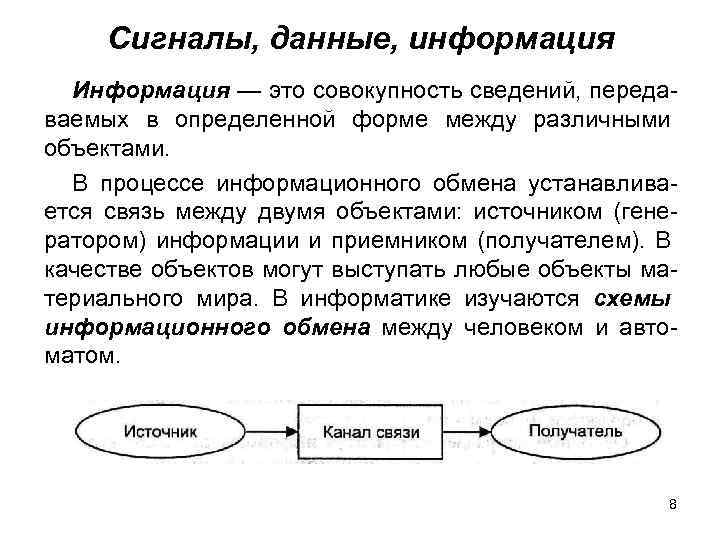Сигналы, данные, информация Информация — это совокупность сведений, передаваемых в определенной форме между различными объектами. В процессе информационного обмена устанавливается связь между двумя объектами: источником (генератором) информации и приемником (получателем). В качестве объектов могут выступать любые объекты материального мира. В информатике изучаются схемы информационного обмена между человеком и автоматом. 8

Сообщения — это совокупность знаков или сигналов, отображающих ту или иную информацию. Физический процесс, несущий передаваемое сообщение в пространстве и во времени, называется сигналом. Линией связи называется физическая среда, используемая для передачи сигналов. Данные — это зарегистрированные сигналы, представленные в форме, пригодной для хранения, передачи и обработки информации. Система передачи информации состоит из источника, передатчика, канала связи, приемника и получателя информации. Информационный процесс — это последовательность действий, производимых с информацией. Наиболее значимыми информационными процессами являются процессы сбора, передачи, преобразования, обработки, накопления, хранения и использования информации. 9

2. Атрибутивные свойства информации Формы представления информации Существует множество форм и видов представления информации. По способу восприятия информации через органы чувств различают: визуальную, звуковую, тактильную, ароматическую и вкусовую информацию. Форма восприятия информации тесно связана с понятием пользовательского интерфейса. Особое значение имеет визуальная и звуковая информация. 10

Визуальная информация может быть представлена в знаковой, графической и табличной форме, а звуковая — в виде устной словесной (вербальной) и музыкальной формы. Для хранения информации используются различные материальные носители информации (книги, пластинки, оптические диски и т. д. ) При компьютерном хранении и обработке информации все формы информации кодируются, т. е. каждому значению некоторой физической величины присваивается числовое значение. Этот процесс имеет еще одно название — оцифровка. 11

Показатели качества информации Качественные характеристики информации определяет получатель информации. Одна и та же информация с точки зрения одного получателя может быть очень важной и ценной, а с точки зрения другого нет. Основными свойствами информации являются структурированность, смысл и ценность. Структурированность, или синтаксические характеристики информации, позволяют выделять информацию из получаемых сигналов. Смысл, или семантические характеристики информации, позволяют определить цель, назначение и практическую значимость информации (прагматические характеристики). Ценность информации выражается в таких понятиях, как содержательность, актуальность, своевременность, адекватность, полнота и достоверность. 12

3. Системы счисления Позиционные системы счисления Системой счисления называют способ записи чисел. В позиционной системе значение числа определяется символами, принятыми в системе, и положением (позицией) этих символов в числе. В общем виде запись числа в позиционной системе счисления имеет вид: А = аn-1 рn-1 + … + а 0 р0 + а-1 р-1 + … + а-i р-i + … + а-m р-m, где р — основание системы счисления; аi — коэффициенты целой и дробной части числа; n — разрядность целой части числа; т — разрядность дробной части числа. 13

Общий вид записи числа в позиционной системе счисления позволяет переводить числа, записанные в системе счисления с любым основанием, в десятичную систему. Например, запись двоичного числа 1100, 011 будет иметь вид: А = 1· 23 + 1· 22 + 0· 21 + 0· 20 + 0· 2 -1 + 1· 2 -2 + 1· 2 -3 = = 8 + 4 + 0 + 0, 25 + 0, 125 = 12, 375. Арифметические действия с числами любой позиционной системы счисления производятся по тем же правилам, что и в десятичной системе. Например, пусть требуется сложить два числа (58 и 68) в восьмеричной системе счисления. Сумма 58 и 68 больше основания системы счисления 8, поэтому необходимо произвести перенос единицы в старший разряд и записать остаток в младшем разряде. Получим 138. 14

Перевод чисел из одной системы счисления в другую Для перевода чисел из одной системы счисления в другую разработаны специальные правила, причем целая часть числа переводится по одним правилам, а дробная по другим. Для перевода целой части число последовательно делится на основание системы счисления. Остаток от деления будет являться одним из разрядов искомого числа. Рассмотрим пример. Пусть требуется перевести число 12 в двоичную систему счисления. Делим число 12 на 2 (остаток — 0), результат деления 6 делим на 2 (остаток — 0), результат деления 3 делим на 2 (остаток — 1), результат деления 1, процесс перевода закончен, получаем 1100. 12 1 -й остаток деления (нулевой разряд)→ 2 (0) 6 2 (0) 3 2 (1) 1 2 -й остаток деления (первый разряд)→ 3 -й остаток деления (второй разряд)→ 15

Для перевода дробной части число последовательно умножается на основание системы счисления. Целая часть будет являться одним из разрядов после запятой искомой дроби. Рассмотрим пример. Пусть требуется перевести десятичную дробь 0, 375 в двоичную систему счисления. Умножаем 0, 375 на 2 (целая часть произведения — 0), дробную часть произведения 0, 750 умножаем на 2 (целая часть произведения — 1), дробную часть произведения 0, 5 умножаем на 2 (целая часть произведения — 1), дробная часть произведения 0, процесс перевода закончен, получаем 0, 011. 0, 375 х 2 = 0, 75 ← целая часть 0 (1 -й разряд двоичной дроби) 0, 75 х 2 = 1, 5 ← целая часть 1 (2 -й разряд двоичной дроби) 0, 5 х 2 = 1 ← целая часть 1 (3 -й разряд двоичной дроби) 16

Для того чтобы перевести в двоичную систему счисления смешанное десятичное число, необходимо выделить дробную и целую часть числа, а затем воспользоваться сформулированными выше правилами. Например, пусть дано число 12, 375. Переведем целую часть числа (12) в двоичную систему, получим 1100. Переведем дробную часть числа (0, 375) в двоич-ную систему, получим 0, 011. Сложим дробную и целую части, получим 1100, 011. Программа Калькулятор, входящая в состав стандартных приложений Windows, при выполнении вычислений, кроме десятичной системы счисления может использовать двоичную, восьмеричную и шестнадцатеричную системы. Для этого Калькулятор надо перевести в инженерный вид, после чего появятся переключатели систем счисления (16 -Нех, 10 -Dec, 8 -Oct, 2 -Bin). Число, набранное в поле ввода, автоматически переводится в другую систему счисления. При преобразовании дробных чисел в другую систему счисления его дробная часть автоматически отбрасывается. 17

4. Меры и единицы количества и объема информации Имеется несколько подходов, которые устанавливают количество информации в сообщении, при этом учитываются синтаксические и семантические характеристики информации. Комбинаторный подход Количество информации в комбинаторной мере — это число возможных комбинаций информационных элементов. Размещениями из n элементов по т называются такие их соединения, которые различаются друг от друга самими элементами и их порядком. Например, размещения из трех элементов А, В, С по 2: АВ, АС, ВА, СВ. Число всех размещений из n различных элементов по т равняется n!/(n-т)!. 18

Перестановками из n элементов называются их соединения, отличающиеся друг от друга только порядком входящих в них элементов. Например, перестановки из трех элементов А, В, С: ABC, АСВ, ВСА, ВАС, CAB, CBA. Число перестановок из n элементов равняется n!. Сочетаниями из n элементов по т называются их соединения, отличающиеся друг от друга только самими элементами. Например, сочетания из трех элементов А, В, С по 2: АВ, АС, ВС. Число всех сочетаний из n различных элементов по т равняется n!/((n-т)!т!). 19

Алфавитный подход Количество информации I, приходящееся на один символ сообщения, определяют по формуле Хартли: I = log 2 N, где N — число возможных символов, которое может использоваться при передаче сообщения. Например, при передаче символов русского алфавита, который содержит 33 буквы, количество информации будет равно I = log 233 = 5, 04. Это значит, что для кодирования 33 -х букв требуется 6 бит. 20

Статистический подход базируется на понятии энтропии и служит для оценки меры информационной неопределенности, учитывающей вероятность появления событий. Количество информации определяется, как мера уменьшения неопределенности знаний о передаваемой информации. Формула Шеннона: где N — число возможных символов, которое может использоваться при передаче сообщения; pi — вероятность появления i-го символа в сообщении. Количество информации, определяемое по формуле Шеннона, называют информационной энтропией. Энтропия при равенстве всех вероятностей имеет наибольшее значение, при этом формула Шеннона совпадает с формулой Хартли. 21

Единицы измерения информации Минимальной единицей измерения информации является бит. Бит - это количество информации, которое можно записать в одном двоичном разряде. Двоичный разряд может принимать значение 1 или 0. Байт равняется 8 битам. Один байт может принимать 256 различных значений, (т. е можно закодировать 256 различных символов). Более крупными единицами информации являются килобайты (К), мегабайты (М), гигабайты (Г) и терабайты (Т). По определению: 1 килобайт = 1024 байт. 1 Кбайт = 210 байт = 1024 байт. 1 Мбайт = 220 байт = 1024 Кбайт. 1 Гбайт = 230 байт = 1024 Мбайт. 1 Тбайт = 240 байт = 1024 Гбайт. 22

5. Кодирование данных в ЭВМ Кодирование чисел Для кодирования чисел используются 1, 2, 4, 8, 16 байт. Если число представляется на внутримашинном уровне, то на его хранение отводятся, по крайней мере, два байта. При хранении чисел один бит (крайний левый) отводится под знак числа. 23

В вычислительной технике, с целью упрощения выполнения арифметических операций, применяют специальные коды (прямой, обратный и дополнительный). За счет этого облегчается определение знака результата вычисления арифметической операции, а операция вычитания чисел сводится к арифметическому сложению. Положительные числа хранятся в прямом коде, а отрицательные числа в дополнительном. Прямой двоичный код — это такое представление двоичного числа, при котором знак плюс кодируется нулем в старшем разряде числа, а знак минус — единицей. При этом старший разряд называется знаковым. Например, числа +510 и -510, представленные в прямом четырехразрядном коде, выглядят так: +510 = = 0. 1012; -510 = 1. 1012. Здесь точка условно отделяет зна-ковые разряды. 24

Обратный код для отрицательных чисел получается из прямого кода с помощью инверсии, при которой единицы незнаковых разрядов заменяются нулями, а нули заменяются единицами. Например, число -510 в обратном коде выглядит так 1. 0102 Дополнительный код для отрицательных чисел получается из обратного кода добавлением единицы к младшему разряду кода. Например, число -510 в дополнительном коде выглядит так 1. 0112. Для положительных чисел прямой, обратный и дополнительный коды совпадают. 25

Для дробных чисел используется формат хранения с плавающей точкой. При этом число предварительно преобразуется в нормализованную форму n = т·q p, где т (<1) — мантисса числа; q — основание системы счисления; р — порядок числа. Пусть дано число в десятичной системе счисления 12, 375. Преобразуем его в нормальную форму 12, 375 = 0, 12375*102. Пусть дано число в двоичной системе счисления 1100, 011. Преобразуем его в нормальную форму: 1100, 011 = 0, 1100011*2100. 26

При хранении дробных чисел часть битов отводится для мантиссы числа, часть — для хранения порядка числа, а в крайнем левом бите хранится знак. Мантисса числа выражается в прямом коде, как для положительных, так и для отрицательных чисел. Различие проявляется только в значении знакового разряда. 27

Кодовые таблицы При вводе информации каждый символ (буквы, цифры, знаки пунктуации и др. ) кодируются определенной последовательностью двоичных цифр в соответствии с международными стандартами кодирования, которые называются таблицами кодирования. Наиболее широкое распространение имеет кодовая таблица ASCII (American Standard Code for Information Interchange). В первой части таблицы (коды 0 — 127) содержатся коды латинских букв, цифр, знаков препинания и управляющих символов. Вторая часть таблицы (коды 128 — 255) предназначена для размещения символов национального алфавита. В разных странах, в разных операционных системах могут использоваться различные варианты второй половины кодовой таблицы, их называют расширениями ASCII. 28

Система кодировки Unicode предназначена для поддержки символов национального алфавита. Набор знаков в кодировке Unicode имеет несколько форм представления. В большинстве случаев используется двухбайтная кодировка, что позволяет закодировать 65 536 символов. 29

Кодование растровых изображений Растровое изображение формируется из множества отдельных точек (пикселей). Каждая точка характеризуется положением и цветом. Глубина цвета — это число разрядов, отводимых для кодирования цвета каждой точки, т. е. количество битов на один пиксель. Глубина цвета измеряется в битах. Черно-белые штриховые изображения кодируются одним битом. Для кодирования 256 полутонов оттенков серого цвета требуется 1 байт — этот формат кодирования черно-белых изображений является в настоящее время общепринятым. 30

Для кодирования растра цветного изображения используются различные стандарты кодировки: стандарт 256 цветов (1 байт) позволяет кодировать 256 оттенков цвета; стандарт High Color (2 байта) позволяет кодировать до 65 тыс. цветовых оттенков; стандарт True Color (3 байта) позволяет кодировать 16, 7 млн. различных цветов. Этот формат в своей основе имеет три основных цвета: красный (Red, R), зеленый (Green, G) и синий (Blue, В). Каждый цвет имеет 256 оттенков и кодируется 1 байтом. В результате смешения трех основных цветов получается 16, 7 млн. оттенков. Такая система кодирования называется RGB по первым буквам названий основных цветов. 31

6. Основные понятия алгебры логики Алгебра высказываний Высказывание - это повествовательное предложение, которое либо истинно, либо ложно. В высказывании говорится о единственном событии. Высказывание «Москва — столица России» является истинным, а высказывание «Волга впадает в Черное море» — ложным. Не всякое предложение является высказыванием. К высказываниям не относятся вопросительные и восклицательные предложения; предложения, в которых не может быть единого мнения о том, истинны они или ложны. 32

Из двух предложений можно образовать новые предложения с помощью союзов: «И» , «ИЛИ» , «ЕСЛИ. . . ТО. . . » , «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» , также с помощью частицы «НЕ» или словосочетания «НЕВЕРНО, ЧТО» , которые в алгебре высказываний называются логическими связками. Высказывания обозначаются большими буквами латинского алфавита. Высказывания принимают значения «истина» (1) или «ложь» (0). В алгебре высказываний определены действия над высказываниями, в результате выполнения которых получают новые высказывания. Пусть А и В простые высказывания. 33

Инверсией (отрицанием) называется логическая операция, проводимая с одним высказыванием, с помощью связки «НЕВЕРНО, ЧТО» . Обозначения инверсии: ¯, NOT, НЕ. А читается, как «неверно, что А» . Конъюнкцией (логическим умножением) называется операция объединения простых высказываний в одно с помощью союза «И» . Обозначения конъюнкции: *, ʌ, &, AND, И. А&В читается, как «А и В» . Дизъюнкцией (логическим сложением) называется операция объединения простых высказываний в одно с помощью союза ИЛИ. Обозначение дизъюнкции: +, v, OR, ИЛИ. Av. В читается, как «А или В» . Импликацией (логическим следованием) называется операция объединения двух простых высказываний в одно с помощью союза «ЕСЛИ …, ТО. . . » . Обозначение импликации: =>. А=>В читается, как «если А, то В» или «из А следует В» . 34

Эквивалентностью (логическим равенством) называется операция объединения двух простых высказываний в одно с помощью союза «ТОГДА И ТОЛЬКО ТОГДА, КОГДА. . . » . Обозначение эквивалентности: <=>. А<=>В читается, как «А эквивалентно В тогда и только тогда, когда из А следует В и из В следует А» . Неэквивалентностью (логическим неравенством, исключающим ИЛИ) называется операция объединения двух простых высказываний в одно с помощью союза «ТОГДА И ТОЛЬКО ТОГДА, КОГДА. . . » . Обозначения: , XOR. А В читается, как «А не эквивалентно В тогда и только тогда, когда из А не следует В а из В не следует А» . При определении значения логического выражения учитывают старшинство или приоритет логических операций: сначала выполняется инверсия, затем конъюнкция, а потом дизъюнкция. Для изменения указанного порядка используют скобки. 35

Таблица истинности Высказывания, образованные при помощи операций логического сложения, умножения и отрицания, называют сложными высказываниями. Истинность всякого сложного высказывания устанавливают с помощью таблиц истинности, которые содержат всевозможные комбинации значений входных переменных вместе с соответствующими им значениями выходных переменных. 36

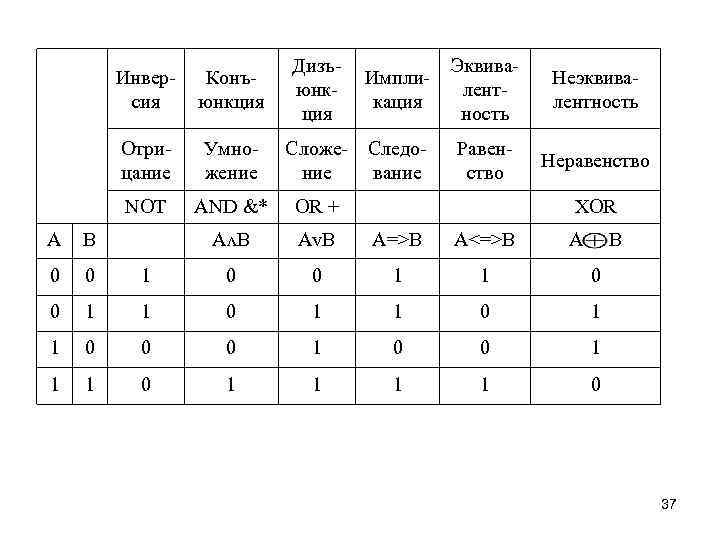Дизъюнкция Импликация Эквивалентность Неэквивалентность Равенство Неравенство Инверсия Конъюнкция Отрицание Умножение NOT AND &* OR + АʌВ Av. В А=>В А<=>В Сложе- Следоние вание XOR А В 0 0 1 1 0 1 1 0 0 0 1 1 1 0 37

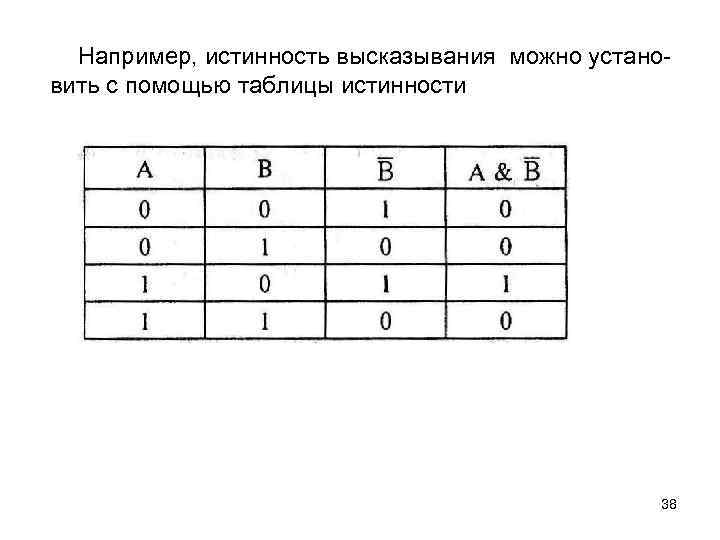Например, истинность высказывания можно установить с помощью таблицы истинности 38

Тождественные преобразования над высказываниями Высказывания, у которых совпадают таблицы истинности, называются равносильными. При тождественных преобразованиях можно заменять высказывания, входящие в формулу, равносильными. Равносильности формул логики высказываний называют законами логики. Законы формальной логики, сформулированные Аристотелем: закон тождества: в ходе рассуждений истинностные значения высказываний не должны изменяться; закон противоречия, никакое высказывание не может быть истинным и ложным одновременно; закон исключенного третьего: каждое высказывание должно быть либо истинным, либо ложным. 39

Согласно закону двойного отрицания отрицать отрицание высказывания то же, что утверждать это высказывание: . Законы коммутативности (переместительный закон) и ассоциативности (сочетательный закон) конъюнкции и дизъюнкции аналогичны одноименным законам сложения и умножения чисел: А&В=В&А или А*В=В*А; Av. В=Вv. А или А+В=В+А; (А&В)&С=А&(В&С) или (А*В)*С=А*(В*С); (Av. В)v. С=Av(Вv. С) или (А+В)+С=А+(В+С). 40

В силу законов идемпотентности в алгебре логики нет «показателей степеней» и «коэффициентов» ; конъюнкция одинаковых «сомножителей» равносильна одному из них, дизъюнкция одинаковых «слагаемых» равносильна одному из них: А&А=А или А*А=А Av. А=А или А+А=А Закон дистрибутивности (распределительный закон): (Av. В)&С=(Av. С)v(В&С) или (А+В)*С=(А*С)+(В*С); (А&В)v. С=(Av. С)&(Вv. С) или (А*В)+С=(А+С)*(В+С). 41

Закон двойственности (де Моргана): или ; или . Закон поглощения: Av(A&В)=A или A+(A*В)=A; A&(Av. В)=A или A*(A+В)=A. Закон склеивания: или ; или . 42

7. Логические основы ЭВМ Логический элемент предназначен для преобразования одного или нескольких входных сигналов в выходной. Различают два вида сигналов: логическая единица и логический нуль. Логическая единица соответствует высокому уровню некоторой физической величины, например электрического напряжения, а логический нуль — низкому. На рисунке приведены условные обозначения базовых логических элементов, применяемых в вычислительной технике, а в таблице приведены их соответствующие таблицы истинности. 43

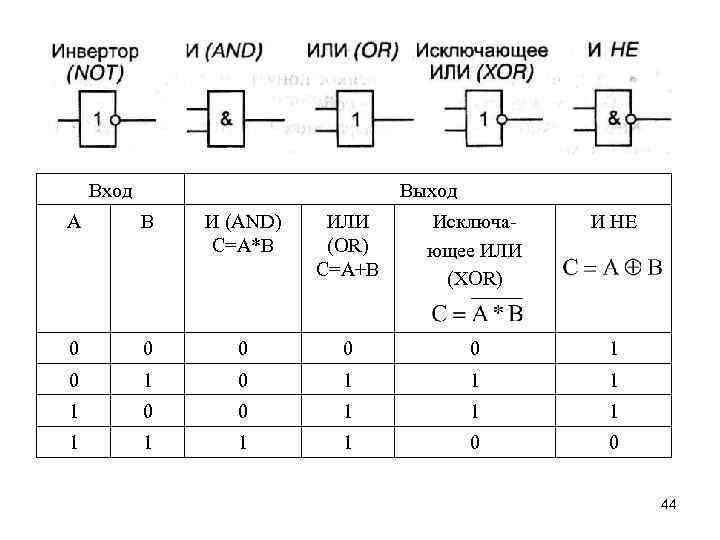Вход Выход А В И (AND) С=А*В ИЛИ (OR) С=А+В Исключающее ИЛИ (XOR) И НЕ 0 0 0 1 0 1 1 0 0 1 1 1 1 0 0 44

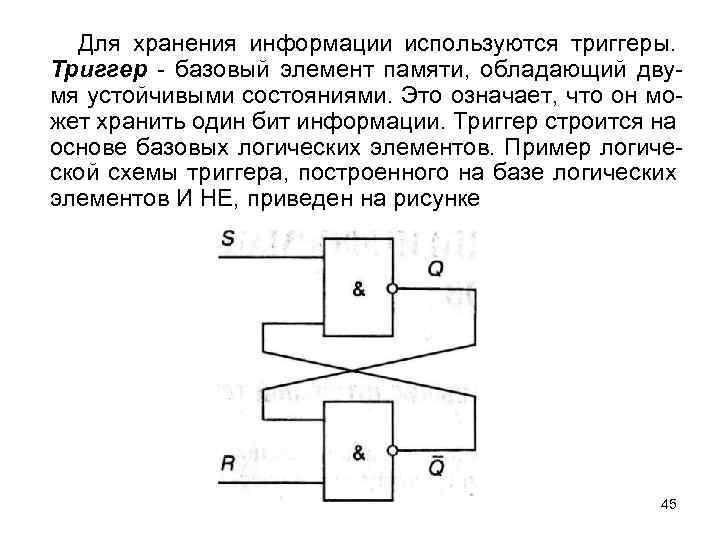Для хранения информации используются триггеры. Триггер - базовый элемент памяти, обладающий двумя устойчивыми состояниями. Это означает, что он может хранить один бит информации. Триггер строится на основе базовых логических элементов. Пример логической схемы триггера, построенного на базе логических элементов И НЕ, приведен на рисунке 45