ИНФОРМАЦИЯ Измерение количества информации В презентации использованы слайды

ИНФОРМАЦИЯ Измерение количества информации В презентации использованы слайды из презентации К. Ю. Полякова

Содержание • • Понятие информации Единицы измерения информации Подходы к измерению информации Количество информации как мера уменьшения неопределенности знания • Количество информации в сообщении (двоичное кодирование) Теория Задачи – Формула Ральфа Хартли – Формула Клода Шеннона • • • Количество информации в сообщении Теория Задачи Кодирование текстовой информации Теория Задачи Кодирование графической информации Теория Задачи Кодирование звуковой информации Теория Задачи Передача информации Задачи

Понятие информации в различных областях науки и техники Информация - это сведения об окружающем мире (объекте, процессе, явлении, событии), которые являются объектом преобразования (включая хранение, передачу и т. д. ) и используются для выработки поведения, для принятия решения, для управления или для обучения. Информация - это любые данные или сведения, которые кого-либо интересуют (толковый словарь русского языка С. И. Ожегова). Информация – это сведения(сообщения, данные) независимо от формы их представления (Федеральный закон Российской Федерации от 27 июля 2006 г. № 149 ФЗ «Об информации, информационных технологиях и о защите информации» ). Информация – это отражение внешнего мира с помощью знаков или сигналов. Под информацией в теории информации понимают не любые сведения, а лишь те, которые снимают полностью или уменьшают существующую до их получения неопределенность. По определению К. Шеннона, информация – это снятая неопределенность. ? Как измерить информацию? Очевидно, это сделать не так просто, т. к. нет её универсального определения.

Единицы измерения 1 байт (bytе) = 8 бит 1 Кб (килобайт) = 1024 байта 1 Мб (мегабайт) = 1024 Кб 1 Гб (гигабайт) = 1024 Мб 1 Тб (терабайт) = 1024 Гб 1 Пб (петабайт) = 1024 Тб 210

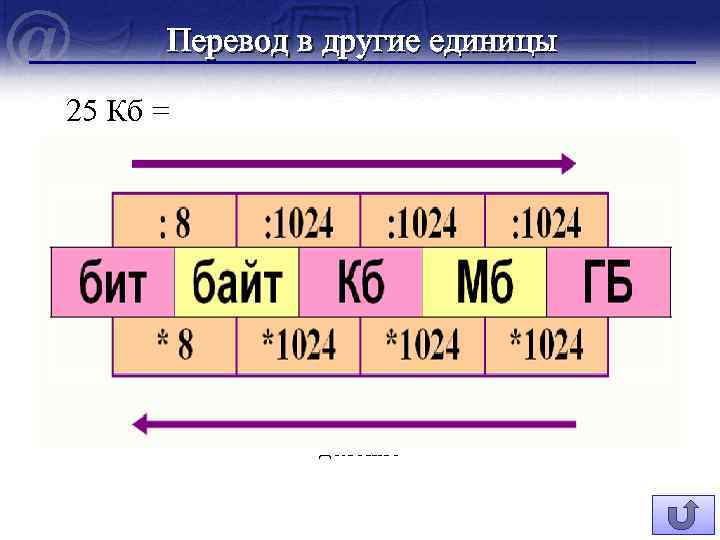Перевод в другие единицы 25 Кб = =25· 1024 байт =25· 1024· 8 бит =25: 1024 Мб =25: 1024=25: 10242 Гб =25: 1024: 1024= 25: 10243 Тб умножение крупные единицы мелкие единицы деление

Подходы к измерению информации Алфавитный • Отталкивается от практических нужд хранения и передачи информации в технических системах; • Не связан со смыслом (содержанием) информации; • Через количество символов с учетом информационного веса каждого символа. Содержательный (вероятностный) • Рассматривает восприятие информации человеком; • Имеет дело со смыслом информации; • Через неопределенность знаний, с учетом вероятности наступления события.

Количество информации как мера уменьшения неопределенности знания Рассмотрим, как можно измерить количество информации на примере подбрасывания монеты: Перед броском существует неопределенность нашего знания. n возможны два события (как упадет монета, предсказать невозможно) После броска наступает полная определенность n мы видим, (получаем зрительное сообщение), что монета находится в определенном положении ( «орел» или «решка» ) n Это сообщение приводит к уменьшению неопределенности нашего знания в два раза, т. к. из двух равновероятностных событий реализовалось одно. Неопределенность знания (N) – это количество возможных вариантов ответов на поставленный вопрос или количество возможных исходов события.

Количество информации как мера уменьшения неопределенности знания При подбрасывании шестигранного кубика: n Возможно получить один результат из шести равновероятных событий N=6 После броска n получаем зрительное сообщение о результате, неопределенность знаний уменьшается в шесть раз

Единицы измерения 1 бит (binary digit, двоичная цифра) – это количество информации, которое мы получаем при выборе одного из двух возможных вариантов (вопрос: «Да» или «Нет» ? ) «Да» или «Нет» или 1 0 Примеры: Эта стена – зеленая? Да. Дверь открыта? Нет. Сегодня выходной? Нет. Это новый автомобиль? Новый. Ты будешь чай или кофе? Кофе.

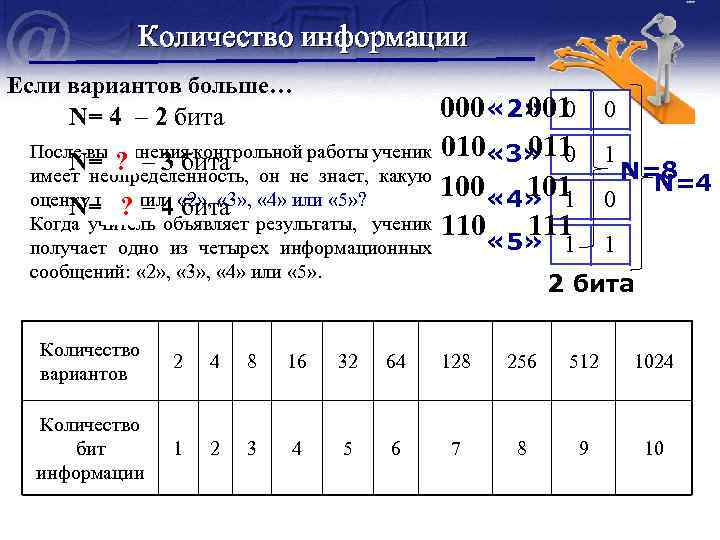Количество информации Если вариантов больше… 000 « 2» 0 001 011 После выполнения контрольной работы ученик 010 « 3» 0 N= 8 – 3 бита он не знает, какую ? имеет неопределенность, 100 « 4» 1 101 оценку получил: « 2» , « 3» , « 4» или « 5» ? N=16 – 4 бита ? Когда учитель объявляет результаты, ученик 110 111 « 5» 0 N= 4 – 2 бита 1 0 N=8 N=4 1 1 получает одно из четырех информационных сообщений: « 2» , « 3» , « 4» или « 5» . 2 бита Количество вариантов 2 4 8 16 32 64 128 256 512 1024 Количество бит информации 1 2 3 4 5 6 7 8 9 10

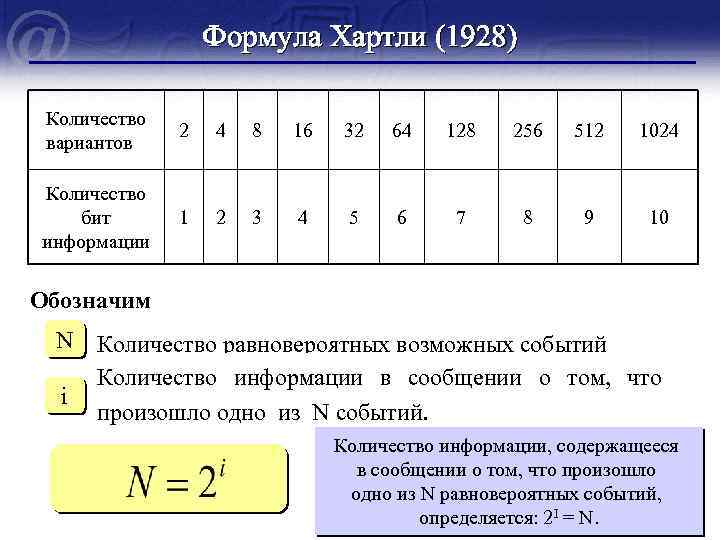Формула Хартли (1928) Количество вариантов 2 4 8 16 32 64 128 256 512 1024 Количество бит информации 1 2 3 4 5 6 7 8 9 10 Обозначим N Количество равновероятных возможных событий Количество информации в сообщении о том, что i произошло одно из N событий. Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется: 2 I = N.

Формула Хартли (1928) ? 6 вариантов – между 4 (2 бита) и 8 (3 бита) i N – количество информации в битах – количество вариантов Пример: В аэропорту стоит 6 самолетов, из них один летит в Москву. Сколько информации в сообщении «В Москву летит второй самолет» ? N=6 бит Ответ: i=2, 585 (количество информации между 2 и 3 битами)

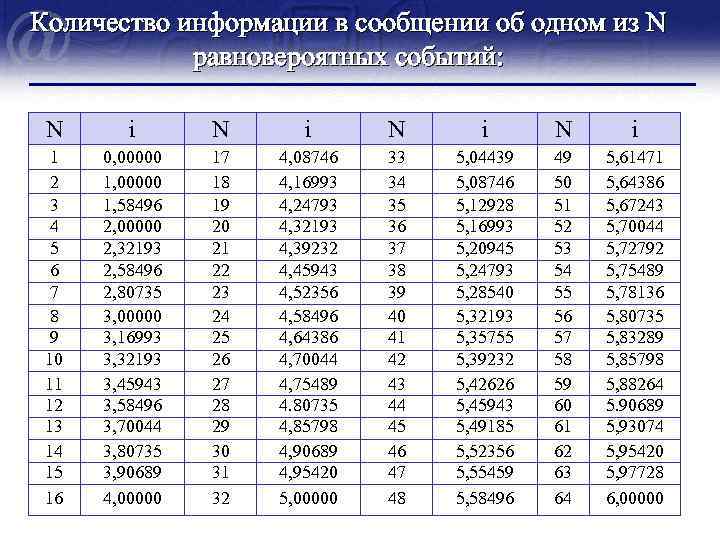Количество информации в сообщении об одном из N равновероятных событий: N i N i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0, 00000 1, 58496 2, 00000 2, 32193 2, 58496 2, 80735 3, 00000 3, 16993 3, 32193 3, 45943 3, 58496 3, 70044 3, 80735 3, 90689 4, 00000 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 4, 08746 4, 16993 4, 24793 4, 32193 4, 39232 4, 45943 4, 52356 4, 58496 4, 64386 4, 70044 4, 75489 4. 80735 4, 85798 4, 90689 4, 95420 5, 00000 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 5, 04439 5, 08746 5, 12928 5, 16993 5, 20945 5, 24793 5, 28540 5, 32193 5, 35755 5, 39232 5, 42626 5, 45943 5, 49185 5, 52356 5, 55459 5, 58496 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 5, 61471 5, 64386 5, 67243 5, 70044 5, 72792 5, 75489 5, 78136 5, 80735 5, 83289 5, 85798 5, 88264 5. 90689 5, 93074 5, 95420 5, 97728 6, 00000

Алфавитный подход Алфавит – набор знаков, используемых при кодировании информации с помощью некоторого языка. Примеры: АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ 32 ABCDEFGHIJKLMNOPQRSTUVWXYZ 26 × O 2 0123456789 10 Мощность алфавита – количество символов. ! Все символы несут одинаковую информацию: информационная емкость символа мощность алфавита

Содержательный подход и вероятность Вероятность события (р) – число от 0 до 1, показывающее, как часто случается это событие в большой серии одинаковых опытов. p = 0 событие никогда не происходит (нет неопределенности) p = 0, 5 событие происходит в половине случаев (есть неопределенность) p = 1 событие происходит всегда (нет неопределенности) pi pз = 1/2 pк =1/2 Полная система событий: одно из N событий обязательно произойдет (и только одно!). – вероятность выбора i-ого варианта (i=1, …, N) p= 1/N pз = 0, 5 pк = 0, 5 pз +pк = 1/2 + 1/2 =1

Содержательный подход и вероятность Вычисление вероятности Задача. В пруду живут 100 рыб, из них 20 карасей, 30 Вероятность показывает какую часть пескарей, а остальные – окуни. Какова вероятность от общего числа событий составляет данное поймать карася (пескаря, окуня), если все рыбы событие (например, ловля окуня). одинаково голодны? Формула: Решение: караси пескари окуни число «нужных» событий общее число событий ? Как иначе посчитать p 3?

На первый взгляд кажется, что формулы для вычисления информации различны. Первая — через количество событий, вторая — через вероятность: На самом деле это не разные формулы! Первая формула является частным случаем второй, когда вероятность событий одинаковая. • Задача: Ученик за год получил 100 оценок. Одинаковое количество пятерок, четверок, троек, двоек — по 25 штук. Вероятность каждой оценки была бы равна 25/100 = 1/4. Значит, и количество информации будет одинаковым. Посчитаем: Но это та же самая задача о четырех равновероятных оценках, количество равновероятностных вариантов N=4 (оценки: 2, 3, 4, 5)

Вероятностный подход Как посчитать информацию, если варианты не равновероятны? Клод Шеннон (1916 — 2001) американский математик и электротехник, один из создателей математической теории информации и криптографии. Идея: если случается менее вероятное событие, мы получаем больше информации. – вероятность выбора i-ого варианта (n=1, …, N) Если произошло событие n, мы получаем информацию

Вероятностный подход Задача 1. В пруду живут 100 рыб, из них 20 карасей, 30 пескарей, а остальные – окуни. Сколько информации несет сообщение о том, что рыбак поймал карася (пескаря, окуня), если все рыбы одинаково голодны? Формула: Решение: бита карась бита пескарь окунь бит

Вероятностный подход Для оценки средней информативности событий с учетом разной вероятности их благоприятных исходов формула К. Шеннона: i средняя информативность в сообщении о том, что произошло одно из N событий. pn вероятность (частота) наступления событий N количество возможных событий (мощность алфавита) Если: p 1=p 2=…=pn=p (события равновероятны), тогда: Формула Хартли

Вероятностный подход Задача 2. В пруду живут 100 рыб, из них 20 карасей, 30 пескарей, а остальные – окуни. Сколько информации несет сообщение о том, что рыбак поймал какую-нибудь рыбу? Формула: Решение: Карась: Пескарь: Количество информации: Окунь:

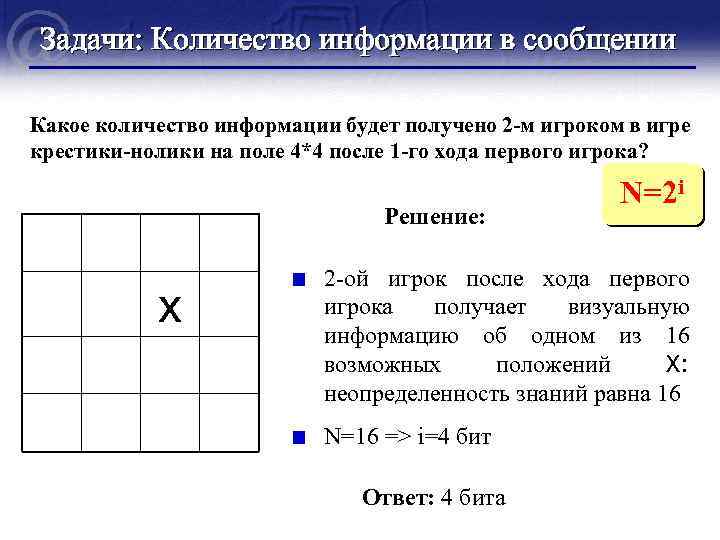Задачи: Количество информации в сообщении Какое количество информации будет получено 2 -м игроком в игре крестики-нолики на поле 4*4 после 1 -го хода первого игрока? Решение: х N=2 i 2 -ой игрок после хода первого игрока получает визуальную информацию об одном из 16 возможных положений Х: неопределенность знаний равна 16 N=16 => i=4 бит Ответ: 4 бита

Задачи: Количество информации в сообщении Была получена телеграмма: ”Встречайте, вагон 4”. Известно, что в составе поезда 8 вагонов. Какое количество информации было получено? Решение: n Количество вагонов равно 8, значит надо выбрать один из 8 вагонов, т. е. N=8 n по формуле N=2 i 8=2 i i=3 бита Примечание: номер вагона (4) на влияет на количество информации, т. к. вероятность событий считаем одинаковой Ответ: 3 бита

Задачи: Количество информации в сообщении В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар? Решение: n считаем общее количество шаров: 8+24=32 n вероятность того, что достали черный шар: n информационный объем сообщения: бита Ответ: 2 бита

Задачи: Количество информации в сообщении В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине? Решение: n сообщение о том, что достали белый шар, несет 2 бита информации, значит количество белых шаров равно N=22=4 n вероятность того, что достали белый шар: Значит вероятность достать черный шар: р ч = n ч / N ч+б = n всего шаров (черных и белых): Ответ: 24 шара

Задачи: Количество информации в сообщении В зоопарке 32 обезьяны живут в двух вольерах, А и Б. Одна из обезьян – альбинос (вся белая). Сообщение «Обезьяна-альбинос живет в вольере А» содержит 4 бита информации. Сколько обезьян живут в вольере Б? Решение: информация в 4 бита соответствует выбору одного из 16 вариантов, т. е. N=16 у нас не было никакой предварительной информации о том, где живет альбинос, поэтому можно считать, что вероятность определяется количеством обезьян в вольере – вероятность равна 1/16, это значит в вольере живет 1/16 часть всех обезьян всего обезьян – 32, поэтому в вольере А живет 32/16 = 2 обезьяны поэтому в вольере Б живут все оставшиеся 32 – 2 = 30 обезьян Ответ: 30 обезьян

Задачи: Количество информации в сообщении Была произведена серия из 11 подбрасываний монетки. В результате каждого подбрасывания монетка может выпасть орлом или решкой с равной вероятностью. Сколько бит информации будет нести в себе сообщение о том, что в этой серии было только четыре выпадения монетки орлом, и все они следовали строго подряд. В ответе укажите целое число. Решение: 1 2 3 4 5 6 7 8 9 10 11 n считаем общее количество событий, для 11 подбрасываний оно равно 211 n количество вариантов благоприятных исходов N=8=23 n вероятность наступления благоприятного исхода равна n бит Ответ: 8 бит

Задачи: Количество информации в сообщении Сколько бит информации несет сообщение о том, что из мешка вытащен белый (серый, черный) камень? Если в мешке 4 белых, 2 серых и 2 черных камня. Решение: всего в мешке: 4+2+2=8 камней вероятность того, что вытащили белый камень: вероятность того, что вытащили серый камень: вероятность того, что вытащили черный камень: количество информации в сообщении о вытаскивании белого камня: серого и черного камней: Ответ: 1 бит, 2 бита

Задачи: Количество информации в сообщении Сколько бит информации несет сообщение о том, что из мешка вытащен один камень? (В мешке 4 белых, 2 серых и 2 черных камня. ) Решение: всего в мешке: 4+2+2=8 камней вероятность того, что вытащили белый камень: вероятность того, что вытащили серый камень: вероятность того, что вытащили черный камень: по формуле Шеннона: Ответ: 1, 5

Количество информации в сообщении Кодирование информации не обязательно должно быть двоичным. Можно использовать не два различных состояния (ноль и один), а больше, в зависимости от выбранного способа передачи/хранения информации. Например: фонарики трех различных цветов, флажки различных видов, палочки четырех различных длин, символы из некоторого алфавита. Количество информации при этом рассчитываться по формуле: — количество различных сигналов (лампочек / символов / объектов), которые используются при кодировании, i — длина последовательности этих сигналов, N — количество различных сообщений, которое можно закодировать, используя последовательность из i сигналов a различных видов. a ai=N Если N не является целой степенью а, то берут i=loga. N+1, то есть округляют (ai < N < a i+1) => N ai

Количество информации в сообщении Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи двух сигнальных флагов, если на корабле имеются флаги трех различных видов (флагов каждого вида неограниченное количество)? а=3 i=2 ai=N Решение: имеются флаги всего трех видов, значит каждый вывешенный сигнальный флаг будет нести в себе количество информации равное 3 битам (один из трех возможных), следовательно сообщение из двух флагов будет нести количество информации равное 32=9 Ответ: 9 сигналов

Количество информации в сообщении Некоторый алфавит содержит три различных символа. Сколько слов длиной ровно в 4 символа можно составить из слов данного алфавита (символы в слове могут повторяться)? Решение: а=3 i=4 ai=N n в алфавите три символа один знак в слове может быть одной из трех возможных символов т. е. несет в себе количество информации равное 3 битам а=3 n в каждом слове по 4 символа, т. е. по четыре знака i = 4 n количество всевозможных четырехбуквенных слов, которое можно составить из данного алфавита N=34=81 Ответ: 81

Количество информации в сообщении Два туристских лагеря, расположенных по разные стороны реки, условились передавать другу сообщения при помощи цветных фонариков красного и зеленого цвета, зажигая или гася их на одну минуту. Каждую минуту наблюдатель с другого берега может зафиксировать одно из трех событий: светит красный фонарик, светит зеленый фонарик, не светит ни один фонарик. Сколько различных сообщений длиной в пять минут можно передать таким способом? Решение: N=ai n одно сообщение длится 1 мин, значит за 5 мин будет получено 5 сообщений i=5 n каждое сообщение может быть одним из трех возможных, поэтому а=3 n N=35=243 Ответ: 243

Количество информации в сообщении Светодиод может находиться в пяти состояниях. Какое минимальное количество светодиодов понадобиться, чтобы собрать индикатор, способный воспроизводить 107 различных сообщений? В ответе укажите целое число. Решение: N аi n Количество различных сообщений , которое необходимо кодировать 107 N=107 n Каждый светодиод имеет 5 состояний: а=5 5 i 107 i 3 Ответ: 3

Количество информации в сообщении Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите в байтах информационный объем результатов наблюдений. Решение: N 2 i V=i*k n всего имеем 101 измерение N=101 n необходимо иметь столько бит, чтобы кодировать 101 различных вариантов, поэтому: 101 2 i i 7 n объем информации для k=80 измерений V=7*80 бит=560 бит=70 байт Ответ: 70 байт

Количество информации в сообщении Обычный дорожный светофор без дополнительных секций подает шесть видов сигналов (непрерывный красный, желтый и зеленый, мигающий желтый, мигающий зеленый, мигающие красный и желтый одновременно). Электронное устройство управления светофором последовательно воспроизводит записанные сигналы. Подряд записано 100 сигналов светофора. В битах данный информационный объем составляет: 1) 360 2) 300 3) 600 4) 100 Решение: N 2 i V=i*k n всего число сигналов N=6, а=2 i=3 бита – для кодирования 1 -го сигнала n k=100 измерений V=3*100 бит=300 бит Ответ: 300 бит

Количество информации в сообщении Какое наименьшее число символов должно быть в алфавите, чтобы при помощи всевозможных трехбуквенных слов, состоящих из символов данного алфавита, можно было передать не менее 80 различных сообщений? Решение: N ai n всего различных сообщений не менее 80 N=80 n все слова трехбуквенные, т. е. состоят из 3 -х символов, поэтому i=3 n 80 а 3 а=5 Ответ: 5 символов

Количество информации в сообщении Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д. ) можно закодировать, используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)? Решение: n всего различных сообщений, состоящих из двух символов длиной 5 букв: N 5 = 25 n различных сообщений, состоящих из двух символов длиной 6 букв: N 6 = 26 n N= N 5 + N 6 =25 + 26=32+64 = 96 Ответ: 96

Кодирование информации Тема 1. Двоичное кодирование

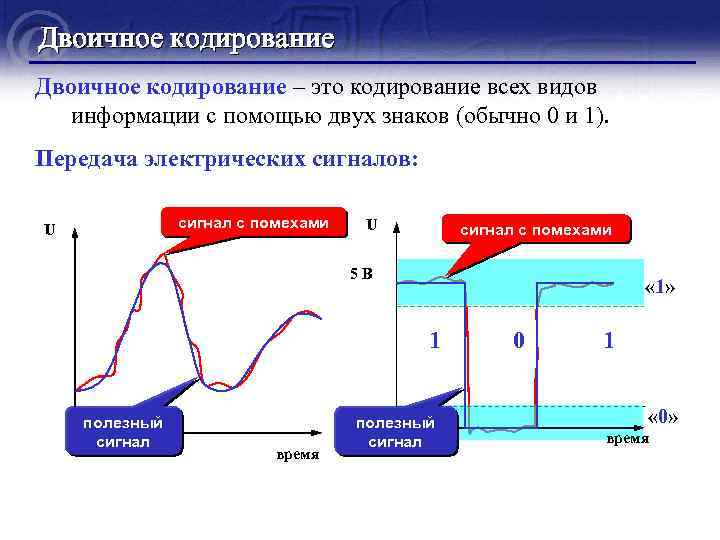Двоичное кодирование – это кодирование всех видов информации с помощью двух знаков (обычно 0 и 1). Передача электрических сигналов: сигнал с помехами U U сигнал с помехами 5 В « 1» 1 0 1 полезный сигнал время полезный сигнал « 0» время

Двоичное кодирование числа символы рисунки кодировщик 10101101110110101 звук видео • в такой форме можно закодировать все виды информации • нужны только устройства с двумя состояниями • практически нет ошибок при передаче • компьютеру легче обрабатывать данные • человеку сложно воспринимать двоичные коды

Кодирование информации Тема 2. Кодирование символов

Кодирование символов Текстовый файл • на экране (символы) • в памяти – двоичные коды 10000012 10000102 10000112 10001002 65 66 67 ! В файле хранятся не изображения символов, а их числовые коды в двоичной системе! А где же хранятся изображения? 68

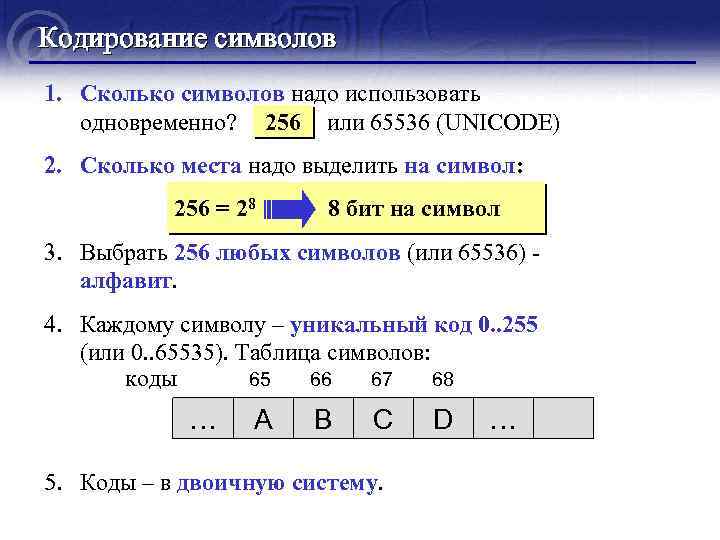Кодирование символов 1. Сколько символов надо использовать одновременно? или 65536 (UNICODE) 256 2. Сколько места надо выделить на символ: 256 = 28 8 бит на символ 3. Выбрать 256 любых символов (или 65536) - алфавит. 4. Каждому символу – уникальный код 0. . 255 (или 0. . 65535). Таблица символов: 65 66 67 68 коды … A B C 5. Коды – в двоичную систему. D …

Кодировка 1 байт на символ 0 127 1 таблица ASCII (международная) 128 254 расширение (национальный алфавит) ASCII = American Standard Code for Information Interchange 0 -31 управляющие символы: 7 – звонок, 10 – новая строка, 13 – возврат каретки, 27 – Esc. 32 пробел знаки препинания: . , : ; ! ? специальные знаки: + - * / () {} [] 48 -57 цифры 0. . 9 65 -90 заглавные латинские буквы A-Z 97 -122 строчные латинские буквы a-z Кодовая страница (расширенная таблица ASCII) для русского языка: CP-866 для системы MS DOS CP-1251 для системы Windows (Интернет) КОИ 8 -Р для системы UNIX (Интернет) 255

Расчет информационного объема текстовой информации Алфавит – набор знаков, используемых при кодировании информации с помощью некоторого языка. Примеры: АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ 32 ABCDEFGHIJKLMNOPQRSTUVWXYZ 26 × O 2 0123456789 10 Мощность алфавита – количество символов. ! Все символы несут одинаковую информацию: i -информационная емкость символа N -мощность алфавита Если в сообщении содержится k символов, общий объем информации вычисляем так V: V=i*k

Задачи: Расчет информационного объема текстовой информации Сколько места в памяти надо выделить для хранение предложения Привет, Вася! n считаем все символы, включая знаки препинания и пробелы (здесь 13 символов) k=13 n если нет дополнительной информации, то считаем, что 1 символ занимает 1 байт n в кодировке UNICODE 1 символ занимает 2 байта Ответ: 13 байт или 104 бита (в UNICODE: 26 байт или 208 бит)

Задачи: Расчет информационного объема текстовой информации Сколько бит нужно выделить для хранения текста МУНСА УРЕ КАМУКА при использовании алфавита племени МУМУКА: буквы МУКАЕНРС и пробел? N 2 i V=i*k Решение: n в алфавите 9 символов (8 букв и пробел) N=9 n 23 < 9 < 24, поэтому на 1 символ нужно выделить 4 бита i=4 n в тексте 16 символов (считая пробелы) k=16 n V=i*k=4· 16 = 64 бита = 8 байт Ответ: 8 байт

Задачи: Расчет информационного объема текстовой информации Сколько места надо выделить для хранения 10 страниц книги, если на каждой странице помещаются 32 строки по 64 символа в каждой? Решение: V=i*kстрок*kсимв. в строке*kстраниц n на 1 странице 32· 64=2048 символов n на 10 страницах 10· 2048=20480 символов n каждый символ занимает 1 байт Ответ: n 20480 байт или … n 20480· 8 бит или … n 20480: 1024 Кб = 20 Кб

Задачи: Расчет информационного объема текстовой информации Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 8 -битном коде, в 16 -битную кодировку Unicode. При этом информационное сообщение увеличилось на 2048 байт. Каков был информационный объем сообщения в байтах до перекодировки? Решение: n пусть х символов в сообщении n первоначально объем сообщения – 8 х бит = х байт n после перекодировки – 16 х бит=2 х байт n Размер сообщения увеличился на 2048 байт или на 2 х-х n 2 х-х=2048 символов n 1 символ – 1 байт 2048 байт Ответ: 2048 байт

Задачи: Кодирование информации Какое максимальное количество бит необходимо для кодирования целых положительных чисел меньших 60? Решение: 1 способ: N 2 i n Количество чисел, которое необходимо кодировать 60 N=60 n Необходимо иметь столько бит, чтобы кодировать 60 различных вариантов, поэтому: 2 i 60 i 6 2 способ: n Число 6010 в двоичной системе счета: 6010 = 1111002 6 бит Ответ: 6 бит

Задачи: Кодирование текстовой информации Объем сообщения, содержащего 1024 символов, составил 1/512 часть мегабайта. Какова мощность алфавита, с помощью которого записано сообщение? N=2 i Решение: n объем сообщения в битах: 1024· 8 бит / 512 = 210· 23 / 29 = 214 бит (= 16348 бит) n на 1 символ приходится 214 / 1024 = 214 / 210 = 24 = 16 бит n мощность алфавита N=216 = 65536 символов Ответ: 65536 символов (кодировка UNICODE)

Задачи: Расчет информационного объема текстовой информации В некоторой стране автомобильный номер состоит из 7 символов. В качестве символов используют 18 различных букв и десятичные цифры в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объем памяти, отводимый этой программой для записи 60 номеров. Решение: V=i*k n мощность алфавита: N=18+10=28 символов n информационный объем одного символа 28 25 i=5 бит n информационный объем одного автомобильного номера, состоящего из 7 символов V=i*k=5*7=35 бит n дополним V=35 бит до целого количества байт V=40 бит=5 байт n для кодирования 60 номеров (k=60) V=5* 60=300 байт Ответ: 300 байт N 2 i

Задачи: Расчет информационного объема текстовой информации В некоторой стране автомобильный номер состоит из 8 символов. Первый символ – одна из 26 латинских букв, остальные семь – десятичные цифры. Пример номера – A 1234567. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным количеством байт. Определите объем памяти, необходимый для хранения 30 автомобильных номеров. Решение: N 2 i V=i*k n n мощность алфавита для кодирования первого символа: N 1=26 символов информационный объем первого символа 26 25 i 1=5 бит мощность алфавита для кодирования цифр: N 2=10 символов i 2=4 бита каждый символ кодируется одинаковым и минимально возможным количеством бит, значит все символы будут кодироваться 5 битами i=5 бит n для кодирования одного номера: V=5*8=40 бит, что равно целому количеству байт V=40 бит=5 байт n для кодирования 30 номеров (k=30): V=5* 30=150 байт Ответ: 150 байт

Задачи: Расчет информационного объема текстовой информации Для передачи сообщений используется алфавит из 32 прописных русских букв (не используется «Ъ» ). Все передаваемые слова содержат ровно по 8 букв. Каждое передаваемое слово начинается с одной из четырех букв (К, Л, М, Н). Остальные буквы в каждом слове могут быть любыми из используемого алфавита. Какое количество информации (в битах) несет произвольная фраза из 10 слов, если для ее кодирования использовалось минимальное количество бит в рамках описанных выше правил. В ответе укажите целое число. i Решение: N=2 n для кодирования первого символа используют один из четырех возможных символов: N 1=4 симв. информационный объем первого символа i 1=2 бит n для кодирования остальных 7 букв используют один из 32 возможных символов: N 2=32 симв. i 2=5 бит n для кодирования одного номера: V=2+5*7=37 бит n для кодирования 10 слов (k=10): V=37* 10=370 бит Ответ: 370 бит

Задачи: Расчет информационного объема текстовой информации Для кодирования номеров автомобилей принята следующая структура данных: • Номер региона (двузначное число от 00 до 99), серия (комбинация из трех букв из набора «А, В, Е, К, М, Н, О, Р, С, Т, У, Х» ), номер (трехзначное число от 000 до 999). • При создании базы данных автомобильных номеров Петя решил хранить каждый номер в виде массива из 8 символов (два символа на номер региона, три символа на серию и три символа на номер), кодируя каждый символ с помощью однобайтной кодировки ASCII. • Вася увидел, что каждый номер уникален и его можно кодировать натуральным числом, используя для хранения любого такого числа одинаковое минимально возможное количество бит. На сколько бит уменьшится объем памяти, необходимый для хранения одного произвольного номера в варианте кодирования Васи по сравнению с вариантом кодирования Пети? В ответе укажите целое число.

Задачи: Расчет информационного объема текстовой информации Решение: V=i*k N 2 i N=ai 1 -я группа Число от 00 до 99 2 -я группа 3 -я группа Комбинация из трех букв из 12 возможных Число от 000 до 999 n для кодирования номера из 8 символов (k=8) в 8 -ми битной кодировке (i=8) требуется: V=i*k=8*8=64 бита В кодировке, используемой Васей: n для кодирования 2 -х первых разрядов (00 99): N 1=100 i 1=7 бит n для кодирования 2 -ой группы (комбинации из трех букв из 12 возможных символов): N=ai=123=1728 символов i 2=11 бит n для кодирования третьей группы (000 999): N 3=1000 i 3=10 бит n информационный объем одного номера: V=7+11+10 бит =28 бит n разность в объеме информации: V=64 -28 =36 бит Ответ: 36 бит

Кодирование информации Тема 3. Кодирование рисунков

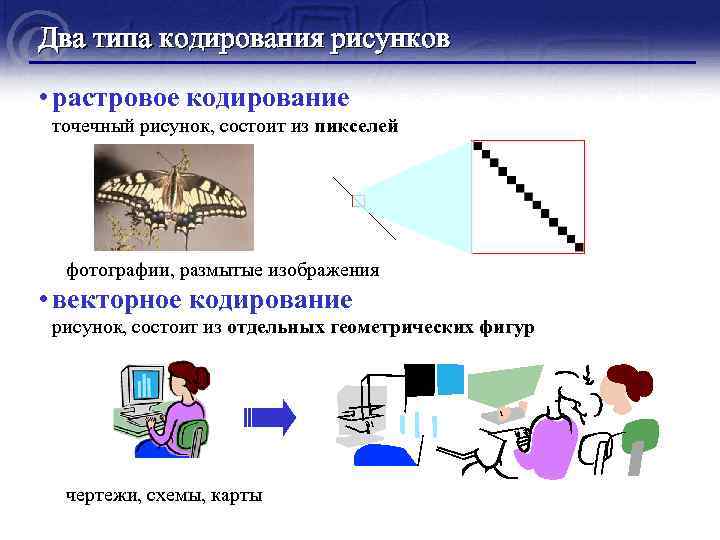Два типа кодирования рисунков • растровое кодирование точечный рисунок, состоит из пикселей фотографии, размытые изображения • векторное кодирование рисунок, состоит из отдельных геометрических фигур чертежи, схемы, карты

Растровое кодирование Шаг 1. Пространственная дискретизация: разбивка на пиксели. Пиксель – это наименьший элемент рисунка, для которого можно независимо установить цвет. Шаг 2. Для каждого пикселя определяется единый цвет. ! Есть потеря информации! • почему? • как ее уменьшить? Разрешение: число пикселей на дюйм, pixels per inch (ppi) экран 96 ppi, печать 300 -600 ppi, типография 1200 ppi

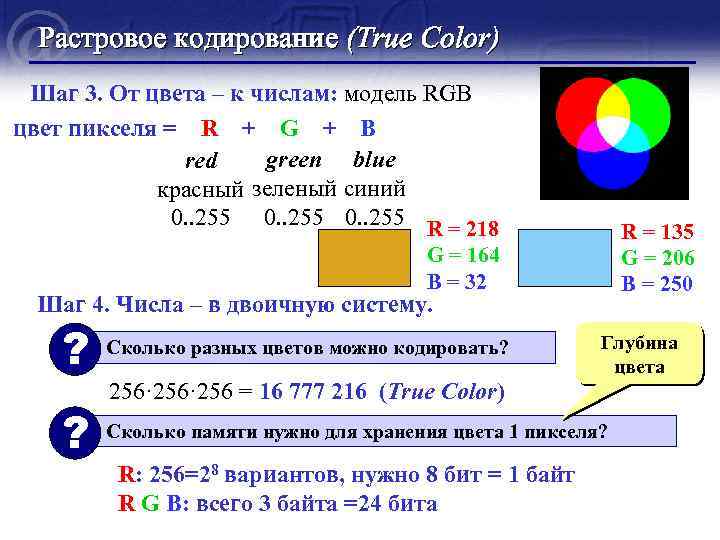Растровое кодирование (True Color) Шаг 3. От цвета – к числам: модель RGB цвет пикселя = R + G + B green blue red красный зеленый синий 0. . 255 R = 218 R = 135 G = 206 B = 250 G = 164 B = 32 Шаг 4. Числа – в двоичную систему. ? Сколько разных цветов можно кодировать? 256· 256 = 16 777 216 (True Color) Глубина цвета ? Сколько памяти нужно для хранения цвета 1 пикселя? R: 256=28 вариантов, нужно 8 бит = 1 байт R G B: всего 3 байта =24 бита

Растровое кодирование с палитрой Шаг 1. Выбрать количество цветов: 2, 4, … 256. Шаг 2. Выбрать 256 цветов из палитры: 248 0 88 0 221 21 181 192 0 21 0 97 Шаг 3. Составить палитру (каждому цвету – номер 0. . 255) палитра хранится в начале файла 255 1 254 0 248 0 88 0 221 21 … 181 192 0 21 0 97 Шаг 4. Код пикселя = номеру его цвета в палитре 2 45 65 14 … 12 23

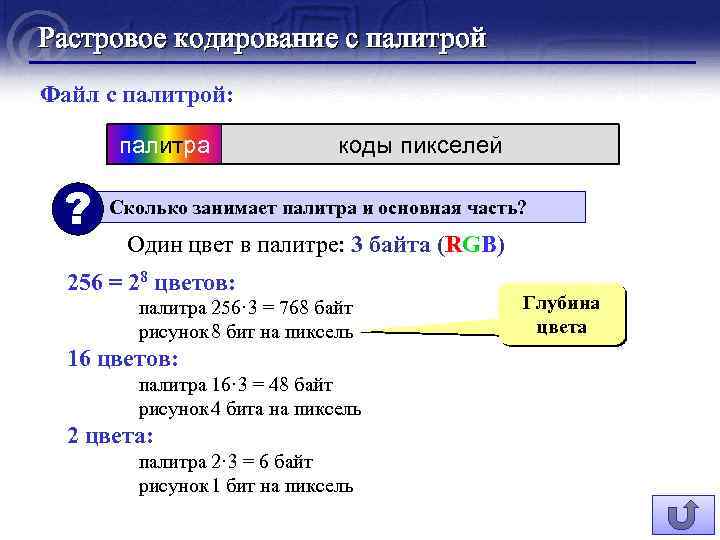Растровое кодирование с палитрой Файл с палитрой: палитра коды пикселей ? Сколько занимает палитра и основная часть? Один цвет в палитре: 3 байта (RGB) 256 = 28 цветов: палитра 256· 3 = 768 байт рисунок 8 бит на пиксель 16 цветов: палитра 16· 3 = 48 байт рисунок 4 бита на пиксель 2 цвета: палитра 2· 3 = 6 байт рисунок 1 бит на пиксель Глубина цвета

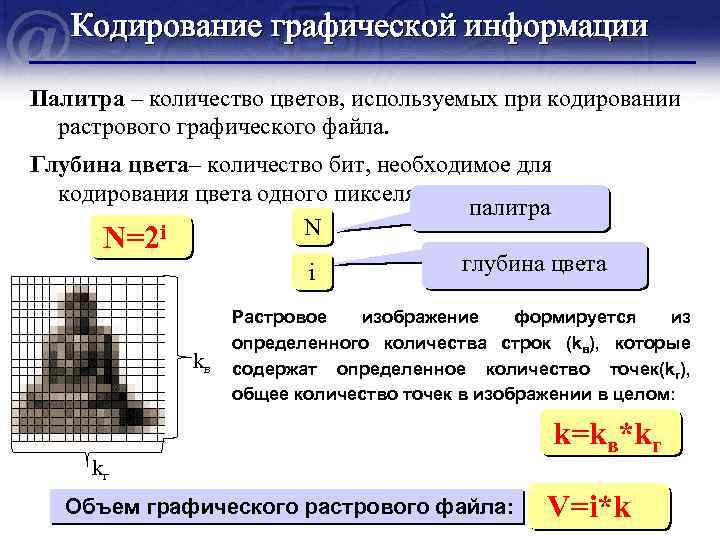Кодирование графической информации Палитра – количество цветов, используемых при кодировании растрового графического файла. Глубина цвета– количество бит, необходимое для кодирования цвета одного пикселя. палитра N N=2 i глубина цвета i kв Растровое изображение формируется из определенного количества строк (kв), которые содержат определенное количество точек(kг), общее количество точек в изображении в целом: kг Объем графического растрового файла: k=kв*kг V=i*k

Задачи: Кодирование графической информации Сколько места в памяти надо выделить для хранения 16 -цветного рисунка размером 32 на 64 пикселя? N=2 V=i*k Решение: n общее число пикселей: k=32· 64=2048 n при использовании 16 цветов N=16 i=4 бита на 1 пиксель (выбор 1 из 16 вариантов) n объем памяти для хранения рисунка: V=i*k=4*2048=8192 бита i Ответ: 8192 бита или … n 2048· 4: 8 байта = 1024 байта или … n 1024: 1024 Кб = 1 Кб

Задачи: Кодирование графической информации Для хранения растрового рисунка размером 32 на 64 пикселя выделили 2 Кб памяти. Каково максимально возможное количество цветов в палитре? V=i*k i=V/k N=2 i Решение: n общее число пикселей: k=32· 64=25 · 26=211 n для хранения рисунка в памяти выделено: V=2 Кб =2 · 210 байта = 211 байта= 214 бита n на 1 пиксель приходится: i=214: 211 = 23 = 8 бит n i=8 бит выбор 1 из 256 вариантов N=28=256 Ответ: не более 256 цветов

Задачи: Кодирование графической информации В процессе преобразования растрового графического файла количество цветов уменьшилось с 1024 до 32. Во сколько раз уменьшился информационный объем файла? N=2 i Решение: n в случае первого кодирования: N 1=1024 i 1=10 бит n во втором случае: N 2=32 i 2=5 бит n каждый пиксель изображения уменьшил свой информационный объем в: n значит, информационный объем всего изображения уменьшился в 2 раза Ответ: в 2 раза

Задачи: Кодирование графической информации После преобразования цветного растрового графического файла (CMYK, 32 бита/пиксель) в черно-белый формат (2 цвета) его размер уменьшился на 31 байт. Сколько пикселей в изображении? В ответе укажите целое число. N=2 i Решение: n пусть в изображении k пикселей, тогда объем файла до преобразования: V 1=32*k бит n для хранения черно-белого изображения используется палитра из двух цветов: N 2=2 i 2=1 бит n объем файла после преобразования: V 2=1*k бит= k бит n размер файла уменьшился на V 1 -V 2=32*k- k=31*k бит или на 31 байт=31*8 бит n 31*k=31*8 k=8 пикселей Ответ: 8

Задачи: Кодирование графической информации После преобразования растрового 256 -цветного графического файла в черно-белый формат (2 цвета) его размер уменьшился на 70 байт. Каков был размер исходного файла? N=2 i Решение: n до преобразования изображения для хранения его в памяти использовали палитру из 256 цветов: N 1=256 i 1=8 бит n пусть в изображении k пикселей, тогда объем файла до преобразования: V 1=8*k бит n после преобразования в ч/б формат используется палитра из двух цветов: N 2=2 i 2=1 бит n объем файла после преобразования: V 2=1*k бит= k бит n размер файла уменьшился на V 1 -V 2=8*k- k=7*k бит или на 70 байт=70*8 бит n 7*k=70*8 k=80 пикселей n исходный размер файла: V=8*80=640 бит Ответ: 640 бит

Задачи: Кодирование графической информации Сколько цифровых фотографий без сжатия разрешением 1024 на 1024 поместится в модуле памяти объемом 512 Мбайт, если каждая точка изображения кодируется четырьмя байтами? Решение: V=i*k n при хранении изображения каждая точка кодируется 4 байтами i=4 байта =22 байта n количество точек в одном изображении: n требуемый объем памяти для одного изображения: n объем памяти, занимаемый всеми изображениями: n количество фотографий: Ответ: 128

Задачи: Кодирование графической информации Цвет пикселя монитора определяется тремя составляющими: зеленой, синей и красной. Под красную и синюю составляющие одного пикселя отвели по 5 бит. Сколько бит отвели под зеленую составляющую одного пикселя, если растровое изображение размером 8 x 8 пикселей занимает 128 байт памяти? Решение: V=i*k n объем изображения: n количество точек в одном изображении: n 1 пиксель изображения занимает: n n для хранения зеленой составляющей палитры: Ответ: 6 i=V/k

Задачи: Кодирование графической информации Книга, состоящая из 272 страниц, занимает объем 2 Мбайта. Часть страниц книги полностью заняты текстом. Каждая такая страница содержит ровно 1024 символа. Другая часть страниц полностью заполнена изображениями с разрешением 768 на 1024 точек. Известно, что страниц с текстом в 16 раз больше, чем страниц с изображениями. Сколько цветов в палитре изображений, если известно, что текстовые символы кодируются двухбайтной кодировкой Unicode? Ответ запишите в виде целого числа.

Задачи: Кодирование графической информации Решение: n пусть в книге х страниц с графикой, тогда страниц с текстом 16 х: n всего в книге х+16 х страниц или 272: х+16 х=272; 17 х=272 х=16 страниц с графикой n 272 -16=256 страниц с текстом n объем всего текста в кодировке Unicode n глубина цвета: n количество цветов в палитре: N=2 i=2 Ответ: 2

Кодирование информации Тема 4. Кодирование звука

Оцифровка (перевод в цифровую форму) цифровой сигнал аналоговый сигнал 10110101010011 аналоговый сигнал ? • • Какой объем информации в аналоговом сигнале? Можно ли хранить его в памяти реального устройства? • Будет ли сигнал на выходе тот же самый? • Почему есть потеря информации?

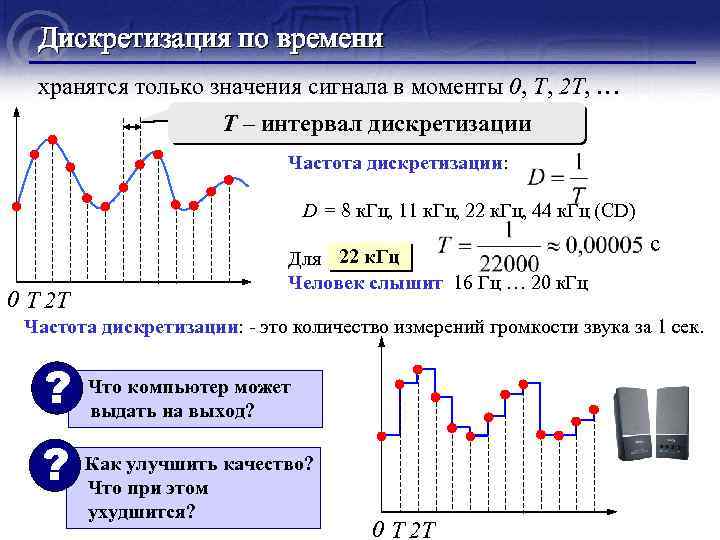Дискретизация по времени хранятся только значения сигнала в моменты 0, T, 2 T, … T – интервал дискретизации Частота дискретизации: D = 8 к. Гц, 11 к. Гц, 22 к. Гц, 44 к. Гц (CD) Для 22 к. Гц Человек слышит 16 Гц … 20 к. Гц 0 T 2 T с Частота дискретизации: - это количество измерений громкости звука за 1 сек. ? Что компьютер может выдать на выход? ? Как улучшить качество? Что при этом ухудшится? 0 T 2 T

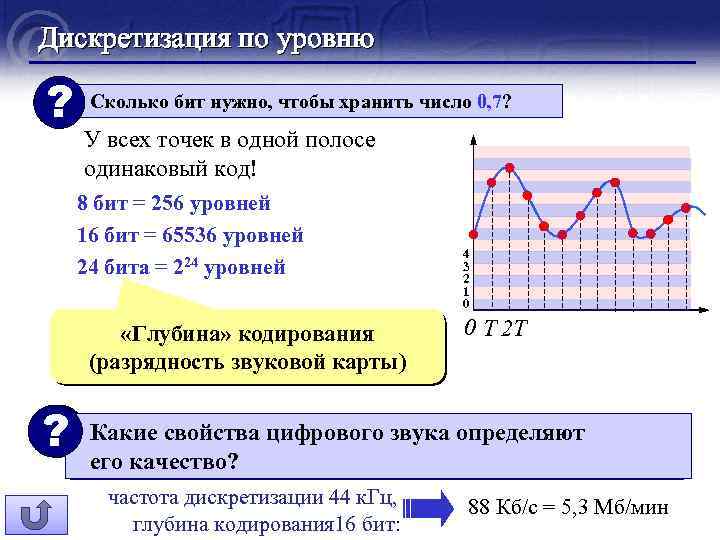Дискретизация по уровню ? Сколько бит нужно, чтобы хранить число 0, 7? У всех точек в одной полосе одинаковый код! 8 бит = 256 уровней 16 бит = 65536 уровней 24 бита = 224 уровней «Глубина» кодирования (разрядность звуковой карты) 4 3 2 1 0 0 T 2 T ! При оцифровке потерю информации дает ? Какие свойства цифрового звука определяют дискретизация как по времени, так и по уровню! его качество? частота дискретизации 44 к. Гц, глубина кодирования 16 бит: 88 Кб/с = 5, 3 Мб/мин

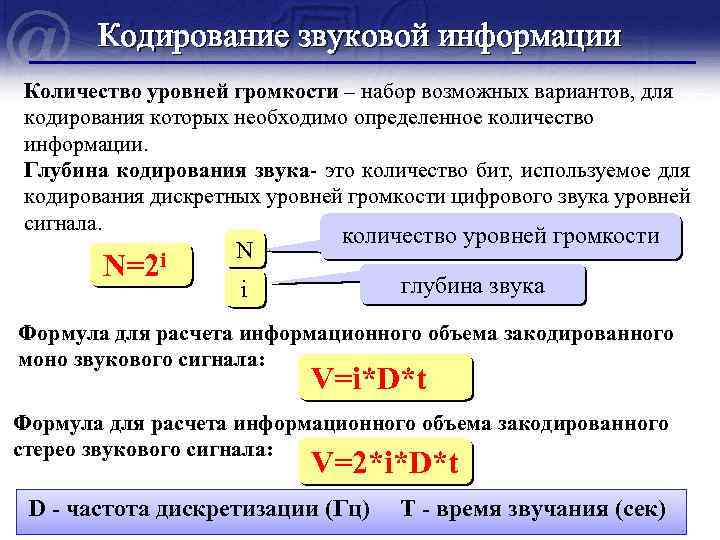Кодирование звуковой информации Количество уровней громкости – набор возможных вариантов, для кодирования которых необходимо определенное количество информации. Глубина кодирования звука- это количество бит, используемое для кодирования дискретных уровней громкости цифрового звука уровней сигнала. N=2 i N i количество уровней громкости глубина звука Формула для расчета информационного объема закодированного моно звукового сигнала: V=i*D*t Формула для расчета информационного объема закодированного стерео звукового сигнала: V=2*i*D*t D - частота дискретизации (Гц) T - время звучания (сек)

Задачи: Кодирование звуковой информации Производится двухканальная (стерео) звукозапись с частотой дискретизации 22 к. Гц и глубиной кодирования 24 бита. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах? 1) 11 2) 12 3) 13 4) 15 Решение: n n глубина кодирования звука i=24 бита=3 байта время звучания: t=2 мин = 120 сек частота дискретизации: D=22 КГц=22000 Гц объем файла: Ответ: 4 15 V=2*i*D*t

Задачи: Кодирование звуковой информации Файл содержал несжатую стереофоническую музыкальную композицию продолжительностью 4 минуты 16 секунд, оцифрованную с 32768 уровнями квантования. После преобразования файла за счет уменьшения количества уровней квантования до 8192 при сохранении частоты дискретизации, его объем уменьшился на 5500 Кбайт. C какой частотой дискретизации был оцифрован файл? В ответе укажите целое число Гц. Решение: V=2*i*D*t n время звучания: t=4 мин 16 сек = 256 сек n изначально уровней квантования: N 1=32768 глубина звука i 1=15 бит n после изменения количества уровней квантования: N 2=8192 глубина звука i 2=13 бит n частота дискретизации осталась неизменной: n объем файла в первом случае: n объем файла во втором случае: n разность между V 1 -V 2=5500 Кбайт Ответ: 44000 Гц

Задачи: Кодирование звуковой информации Файл содержал несжатую стереофоническую музыкальную композицию, оцифрованную с частотой дискретизации 22000 Гц и 65536 уровнями квантования. После преобразования файла за счет уменьшения количества уровней квантования до 4096 при сохранении частоты дискретизации его объем уменьшился на 4125 Кбайт. Какова была продолжительность записанной музыкальной композиции? Решение: N=2 i V=2*i*D*t n изначально уровней квантования: N 1=65536 глубина звука i 1=16 бит n после изменения количества уровней квантования: N 2=4096 глубина звука i 2=12 бит n объем файла в первом случае: n объем файла во втором случае: n разность между V 1 -V 2=4125 Кбайт Ответ: 192 сек

Задачи: Кодирование звуковой информации Модем, передающий информацию со скоростью 128000 бит/с, передал файл с несжатой стереофонической, музыкой за 2 минуты и 45 секунд. Укажите продолжительность (в секундах) записанной в этот файл композиции, если известно, что она была оцифрована с частотой дискретизации 22000 Гц и 256 уровнями квантования. В ответе укажите целое число. Решение: V= t N=2 i V=2*i*D*t n время передачи: t =2 мин 45 сек= 165 сек n при передаче со скоростью 128000 бит/с за 165 сек объем информации: n для записи, использующей 256 уровней квантования: N=256, глубина звука i=8 бит=23 бит Ответ: 60 сек

Задачи: Передача информации Скорость передачи данных через ADSL-соединение равна 256000 бит/c. Передача файла через это соединение заняла 2 минуты. Определите размер файла в килобайтах. Решение: V= t n время передачи: 2· 60 сек=120 сек n передано информации 256 · 1000· 120 бит = 13 8· 23· 125 · 22· 30 бит = 2 · 125· 30 = 2 Кб=3750 Кб 213 Ответ: объем файла 3750 Кб

Задачи: Передача информации Скорость передачи данных через ADSL-соединение равна 128000 бит/c. Через это соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах. Решение: t=V/ n передано информации 625 Кб = 625· 213 бит n время передачи 625· 213 25· 26 25· 16 = 7 = = = 40 с 10 128· 1000 2 · 1000 40 Ответ: 40 с

Задачи: Пердача информации • Три друга — Ваня, Коля и Сергей — совместно используют канал доступа в Интернет с пропускной способностью 96 Мбайт в секунду. Система балансировки нагрузки настроена таким образом, что если в данный момент времени канал использует только один человек, то скачивание файла происходит со скоростью равной пропускной способности канала, а если канал используют несколько человек — пропускная способность канала поровну делится между пользователями. Ваня начал скачивать файл размером 3, 5 Гбайт. Через 8 секунд Коля начал скачивать файл размером 2 Гбайт. Через 16 секунд после этого Сергей начал скачивать файл размером 512 Мбайт. • Через какое время от начала скачивания Ваня полностью скачает свой файл? • Затраты пропускной способности канала на передачу управляющей информации и подтверждений не учитываются. В процессе скачивания файлов никакой дополнительной активности в сети пользователи не проявляют. В ответе укажите целое число секунд.

Ваня VВ=3, 5 Гб Решение: § 3, 5 Гб =3584 Мб; 2 Гб=2048 Мб § 1: Ваня VВ 1=96· 8 Мб=768 Мб Ваня Коля V’В= 3584 -768=2816 Мб V’В =2816 Мб VК=2 Гб § 2: Ваня и Коля VВ 2=VК 2=48· 16=768 Мб t=16 c; =48 Мб/с 2 V’’В=2816 -768=2048 Мб Ваня Коля Сергей ’’ ’’ =2048 Мб ’’ =1280 Мб V =512 Mб V К=2048 -768=1280 Мб V В V К С § 3: Ваня, Коля и Сергей t 3=512/32=16 с VВ 3 = VК 3 =VС =512 Мб t= c; =32 Мб/с 16 3 V’’’В=2048 -512=1536 Мб Ваня Коля Сергей V’’’К=1280 -512=768 Мб ’’’ =1536 Мб ’’’ =768 Мб V ’’’ =0 Мб V В V К С § 4: Ваня и Коля t 4=768/48=16 с VВ 4 = VК 4 =768 Мб t= c; =48 Мб/с 16 4 V’’’’В=1536 -768=768 Мб V’’’В =768 Мб V’’’К=0 МБ § 5: Ваня t 5=768/96=8 с § t=8+16+16+16+8=64 c 5 t= c; =96 Мб/с 8 Ответ: 64 с 1 t=8 c; =96 Мб/с