Информация и информационные процессы Индуктивное определение объектов. Вычислимые функции. Полнота формализации понятия вычислимости.
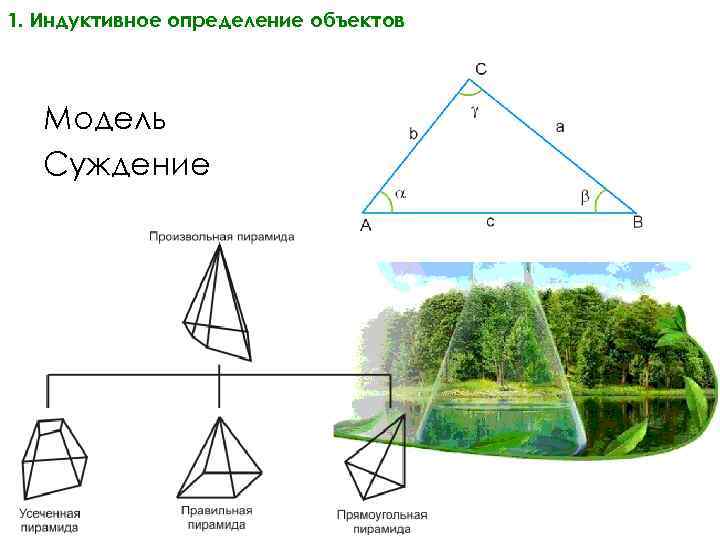
1. Индуктивное определение объектов Модель Суждение
1. Индуктивное определение объектов Понятие — это целостная совокупность суждений о существенных свойствах соответствующего объекта. Понятие – форма мышления, отражающая общие и существенные свойства и отношения вещей и явлений материального мира.
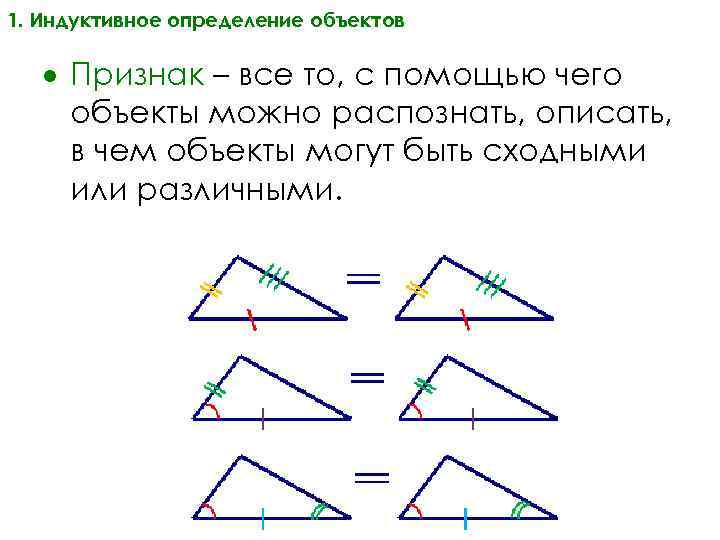
1. Индуктивное определение объектов Признак – все то, с помощью чего объекты можно распознать, описать, в чем объекты могут быть сходными или различными.
1. Индуктивное определение объектов Содержание понятия об объекте - это совокупность взаимосвязанных свойств объекта (целостность). P. S. : когда говорят о математическом объекте, то обычно имеют в виду все множество объектов, обозначаемых одним термином (названием).
1. Индуктивное определение объектов Всякое понятие имеет определенный объем и содержание. Объем понятия — это множество всех объектов, обозначаемых одним и тем же термином. Они взаимосвязаны: чем больше объем понятия, тем меньше его содержание, и наоборот: чем меньше объем, тем больше содержание понятия (Закон обратного отношения)
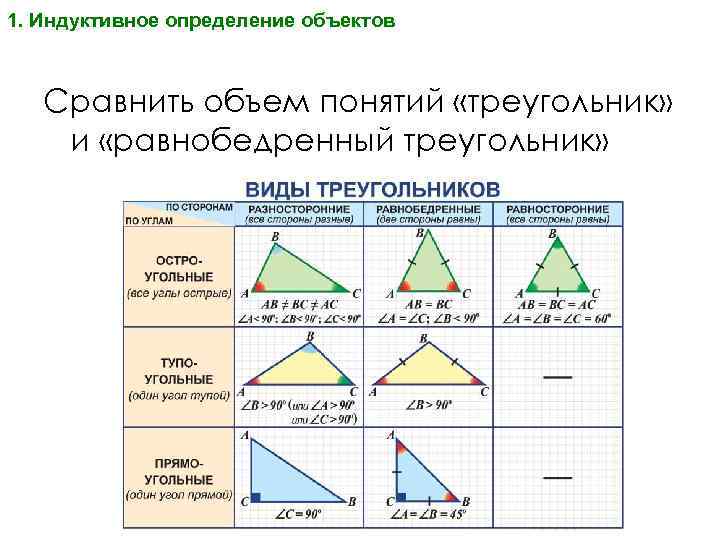
1. Индуктивное определение объектов Сравнить объем понятий «треугольник» и «равнобедренный треугольник»
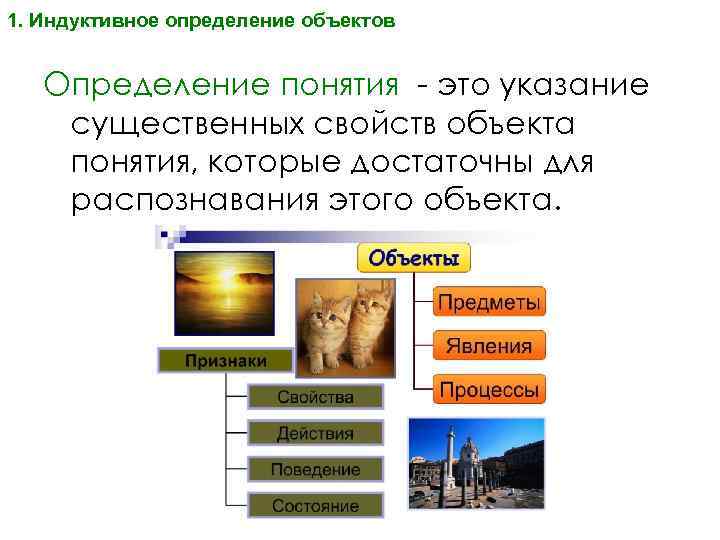
1. Индуктивное определение объектов Определение понятия - это указание существенных свойств объекта понятия, которые достаточны для распознавания этого объекта.
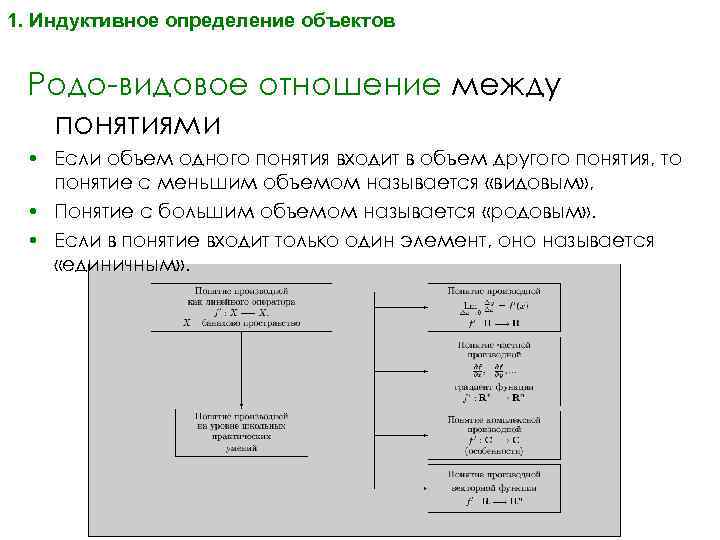
1. Индуктивное определение объектов Родо-видовое отношение между понятиями • Если объем одного понятия входит в объем другого понятия, то понятие с меньшим объемом называется «видовым» , • Понятие с большим объемом называется «родовым» . • Если в понятие входит только один элемент, оно называется «единичным» .
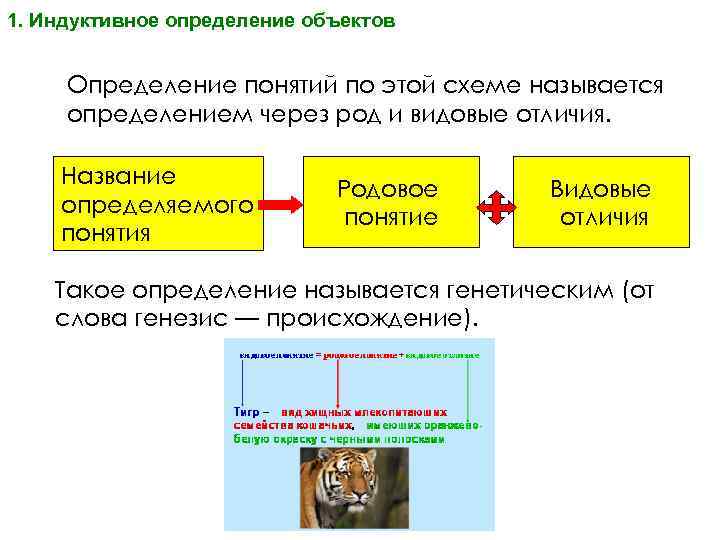
1. Индуктивное определение объектов Определение понятий по этой схеме называется определением через род и видовые отличия. Название определяемого понятия Родовое понятие Видовые отличия Такое определение называется генетическим (от слова генезис — происхождение).
1. Индуктивное определение объектов Индуктивные определения, в которых указывается, как можно получить объекты определяемого понятия один за другим по порядку. (от слова индукция — наведение на умозаключение от частного к общему) или рекуррентное (от слова рекурсия — возвращение).
1. Индуктивное определение объектов Однако не все математические понятия могут быть логически определены указанными выше способами. В конечном итоге определения понятий мы должны прийти к таким понятиям, которые уже не сводимы к другим, т. е. они логически не определяемы. Такие понятия в математике называются первичными или основными.
1. Индуктивное определение объектов Индуктивное определение - один из способов определения объектов математических и логических систем. Состоит в том, что указываются: а) исходные или элементарные объекты системы; б) правила или операции, позволяющие из имеющихся объектов образовывать новые объекты системы. И. о. должно быть полно, т. е. его средствами должны определяться все объекты данной системы, и только они.
1. Индуктивное определение объектов ИО - определение, позволяющее из некоторых исходных объектов теории с помощью некоторых операций строить новые объекты теории. И. о. находят широкое применение в математике, логике и других науках. Примером И. о. натуральных чисел. И. о. состоит из ряда пунктов: 1) 0 является натуральным числом; 2) если п - натуральное число, то п -натуральное число; 3) никаких натуральных чисел, кроме тех, которые получаются согласно применению пунктов (1) и (2), нет.
1. Индуктивное определение объектов Таково же определение четного числа. И. о. состоит из таких пунктов: 1) 0 - четное число; 2) если п - четное число, то п + 2 четное число; 3) никаких (натуральных) чисел, кроме тех, которые порождены применением пунктов (1) и (2), нет.
1. Индуктивное определение объектов Различают два основных вида и. о. : фундаментальные и нефундаментальные. Фундаментальными называются такие и. о. , с помощью которых из исходных объектов порождается та или иная исходная предметная область. Нефундаментальными являются и. о. , с помощью которых из заранее определенной области объектов выделяется некоторое ее подмножество. Приведенные выше и. о. натурального числа и формулы в исчислении высказываний являются фундаментальными, И. о. четного числа является нефундаментальным: предполагается, что область натуральных чисел дана с самого начала или порождена фундаментальным И. о. , а мы на ней определяем некоторое подмножество натуральных чисел (т. е. множество "четные числа").
2. Вычислимые функции — это множество функций вида f: N →N, которые могут быть реализованы на машине Тьюринга. Задачу вычисления функции называют алгоритмически разрешимой или алгоритмически неразрешимой, в зависимости от того, возможно ли написать алгоритм, вычисляющий эту функцию.
2. Вычислимые функции N=B*U {unde f} • где B* - множество слов в двоичном алфавите B={0, 1}, • unde f — специальный элемент, означающий неопределённость.
Задание 1) Перечислить не менее пяти первичных понятий. 2) Сформулировать 3 индуктивных определения из любой предметной области. 3) Рассмотреть алгоритм сложения двух чисел используя тренажер «Машина Поста» . 4) Прослушать лекцию «Вычислимость и логика» .
Скачать презентацию Информация и информационные процессы Индуктивное определение объектов Вычислимые
Индуктивне определение.ppt