Информатика Лекция 3.pptx
- Количество слайдов: 30

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ Лекция 3

Основы алгебры логики (продолжение)

Представление функций АЛ В АЛ также как и в обычной алгебре вводится понятие функции (логическая или булева функция): y=y(x 1, x 2, …, xn) y – логич. функция; x 1, x 2, …, xn – аргументы Логическая функция (ЛФ) - это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции. ЛФ может быть задана: - на словах; - таблично; - алгебраически.

Представление функций АЛ Определим количество различных ЛФ при n аргументах. Число сочетаний для n аргументов: N=2 n , а так как для каждого сочетания аргументов ЛФ может иметь 2 значения (0, 1), то общее количество логических функций

Задание функции одной переменной при n=1 количество ЛФ - F=4 - const 0 (генератор 0) - повторитель - инвертор - const 1 (генератор 1)

Суперпозиция ЛФ Для алгебры логики установлено, что если y= y(z 1, z 2), где z 1=z 1(x 1, x 2) и z 2=z 2(x 3, x 4), то y=y(x 1, x 2, x 3, x 4) Так как ЛФ принимает значение 0 или 1, то мы всегда можем ввести новую переменную, которая будет являться результатом выполнения некоторых логических операций над другими переменными. Т. е. можно считать эту переменную функцией других переменных.

Суперпозиция ЛФ Операция замены одной функции другими, называется суперпозицией. Эта операция дает возможность получить с помощью функций малого количества аргументов функции большего числа аргументов. Так, например, можно получить функцию с требуемым числом аргументов, используя только функцию двух аргументов.

Логические функции двух аргументов Для n=2 F=16 При помощи набора булевых функций двух аргументов можно описать любую цифровую систему. На практике используют не весь набор функций, а только те из них, которые методом суперпозиции обеспечивают представление любой другой функции. Набор таких функций называется функционально полным набором (ФПН).

Логические функции двух аргументов x 1 0 1 1 -ый аргумент x 2 y 0 0 0 1 1 2 -ой аргумент 0 0 Const 0, y 1 0 0 0 1 Конъюнктор, y 2 0 0 1 0 Запрет по x 1, y 3 y 4 0 0 1 1 Повторитель x 2, 0 1 0 0 Запрет по x 2, y 5 0 1 Повторитель x 1, y 6 0 1 1 0 Исключающее «ИЛИ» , y 7 0 1 1 1 Дизъюнктор, y 8 1 0 0 0 Ф-ция Пирса ( «ИЛИ-НЕ» ),

Логические функции двух аргументов (продолжение) x 1 0 1 1 -ый аргумент x 2 y 9 0 0 1 1 2 -ой аргумент 1 0 0 1 Логическая равнозначность, y 10 1 0 Инвертор x 1, y 11 1 0 1 1 Импликация от x 2 к x 1, y 12 1 1 0 0 Инвертор x 2, y 13 1 1 0 1 Импликация от x 1 к x 2, y 14 1 1 1 0 Функция Шеффера ( «И-НЕ» ), y 15 1 1 Const 1,

Функционально полные наборы Существует несколько функционально полных наборов (ФПН). В качестве ФПН можно использовать три основные логические функции «И» , «ИЛИ» , «НЕ» . Это основной ФПН – ОФПН. Кроме ОФПН широкое применение получили: - ФПН, включающий только ф-цию Пирса ( «ИЛИ-НЕ» ); - ФПН, включающий только ф-цию Шеффера ( «И-НЕ» ).

Синтез логических устройств
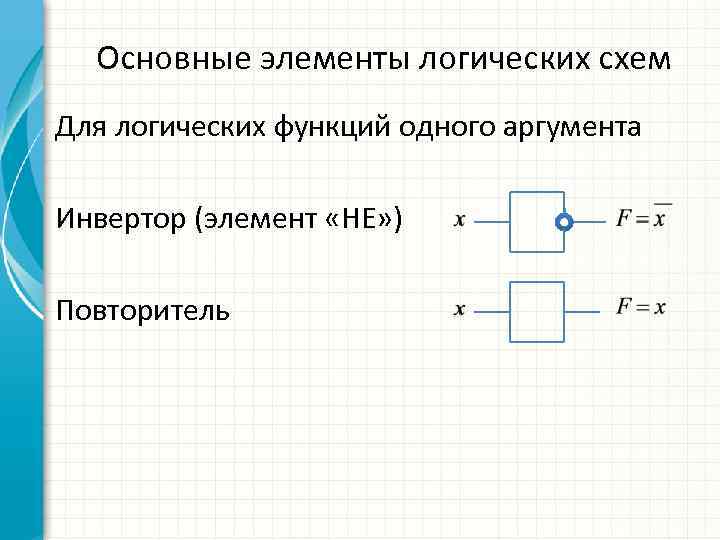
Основные элементы логических схем Для логических функций одного аргумента Инвертор (элемент «НЕ» ) Повторитель
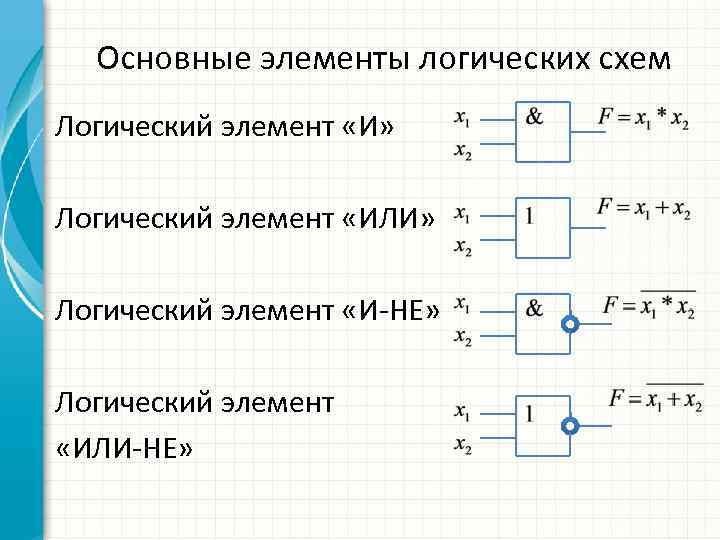
Основные элементы логических схем Логический элемент «И» Логический элемент «ИЛИ» Логический элемент «И-НЕ» Логический элемент «ИЛИ-НЕ»

Синтез логических устройств в базе ОФПН состоит их представления этих функций в нормальных формах и последующей минимизации. Нормальной формой считают представление этих функций посредством суперпозиции вспомогательных функций – минтермов и макстермов.

Синтез логических устройств в базе ОФПН Минтерм – логическая функция, которая принимает значение « 1» только при одном наборе значений аргументов и « 0» – при всех остальных. Макстерм - логическая функция, которая принимает значение « 0» только при одном наборе значений аргументов и « 1» – при всех остальных.
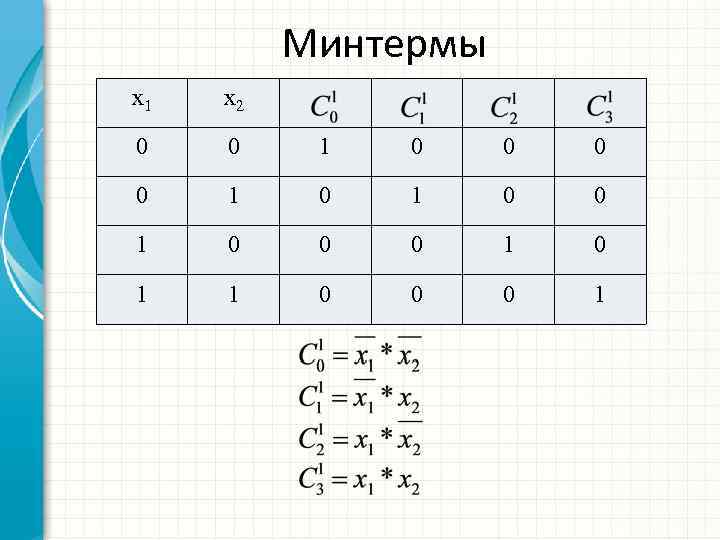
Минтермы x 1 x 2 0 0 1 0 0 1 0 0 0 1

Минтермы Таким образом, любую функцию n аргументов можно представить в виде суперпозиции минтермов: Σ Например, для ф-ции двух аргументов: Такая форма представления логических функций в виде суперпозиции минтермов называется представлением посредством совершенных дизъюнктивных нормальных форм – СДНФ.
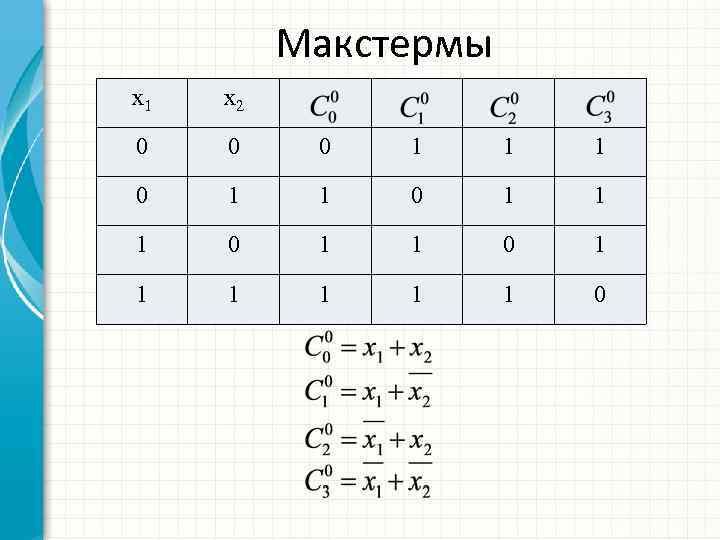
Макстермы x 1 x 2 0 0 0 1 1 1 0 1 1 1 0

Макстермы Аналогично, любую функцию n аргументов можно представить в виде суперпозиции макстермов: Π Например, для ф-ции двух аргументов: Такая форма представления логических функций в виде суперпозиции макстермов называется представлением посредством совершенных конъюнктивных нормальных форм – СКНФ.

Связь минтермов и макстермов Нетрудно заметить, что макстермы являются инверсией минтермов

Пример Представить ф-цию Шеффера в СДНФ x 1 0 1 1 -ый аргумент x 2 0 0 1 1 2 -ой аргумент y 14 1 1 1 0 Функция Шеффера, x 1 x 2 y 14 0 0 1 1 1 0

Пример Представить ф-цию Шеффера в СКНФ x 1 0 1 1 -ый аргумент x 2 0 0 1 1 2 -ой аргумент y 14 1 1 1 0 Функция Шеффера, x 1 x 2 y 14 0 0 1 1 1 0

Синтез логических устройств Синтез проводится в три этапа: 1. Образование СДНФ/СКНФ логической функции по заданной таблице истинности 2. Упрощение этой функции (например, используя законы алгебры логики) 3. Построение соответствующей логической схемы из известных логических элементов (ЛЭ)

Синтез логических устройств Этап 1. Образование СДНФ ЛФ Шаг 1. В заданной таблице истинности выделяем наборы значений аргументов, при которых ЛФ принимает единичные значения. Шаг 2. Для каждого выделенного набора образуем минтерм, принимающий единичное значение при заданном наборе значений аргументов. Шаг 3. Составляем логическую сумму образованных минтермов.

Синтез логических устройств Любой i-й минтерм образуется в виде произведения аргументов, в которые эти аргументы входят без знака отрицания, если в i-м наборе они принимают единичное значение, и со знаком отрицания, если они принимают значение ноль.
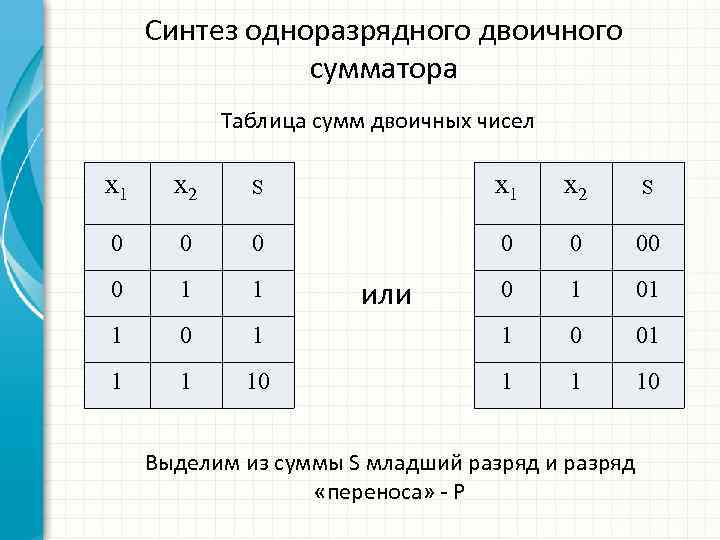
Синтез одноразрядного двоичного сумматора Таблица сумм двоичных чисел x 1 x 2 S 0 0 00 0 1 1 01 1 0 01 1 1 10 или Выделим из суммы S младший разряд и разряд «переноса» - P

Синтез одноразрядного двоичного сумматора Σ X 1 и X 2 – двоичные одноразрядные числа, S - значение суммы P - перенос в старший разряд Таблица истинности для одноразрядного сумматора x 1 x 2 P S 0 0 1 1 0 1 0 0 0 1 1 0
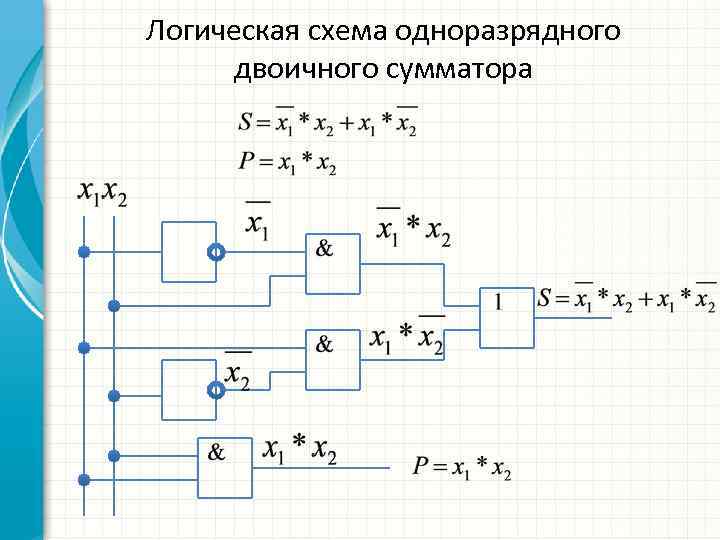
Логическая схема одноразрядного двоичного сумматора
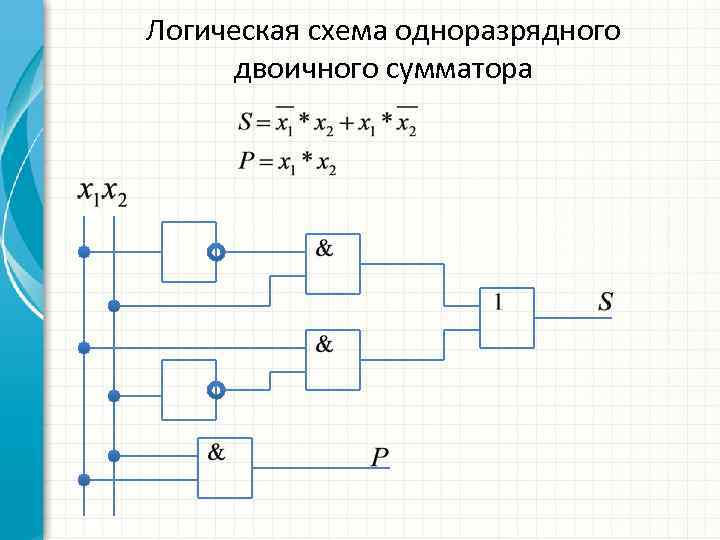
Логическая схема одноразрядного двоичного сумматора
Информатика Лекция 3.pptx