Информационные технологии автоматизированного проектирования Часть 1 Лекция 13

Информационные технологии автоматизированного проектирования Часть 1 Лекция 13

Планируемые типы задач в дисциплине ИТАП 1 Формальное описание коммутационных схем 2 Практическое применение венгерского метода 3 Динамическое программирование. Поиск кратчайшего пути 4 Использование параллельного алгоритма на основе метода обратного размещения 5 Пример использования алгоритма Прима 6 Примеры использования волнового алгоритма 7 Примеры использования модифицированных волновых алгоритмов

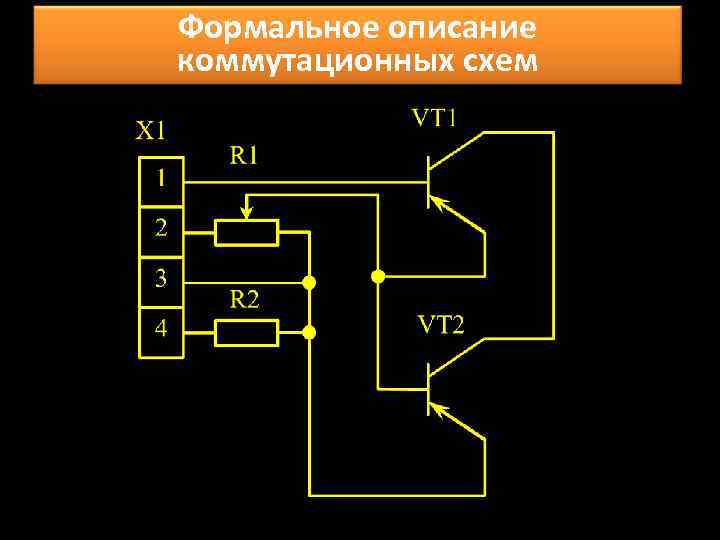Задача 1 Формальное описание коммутационных схем

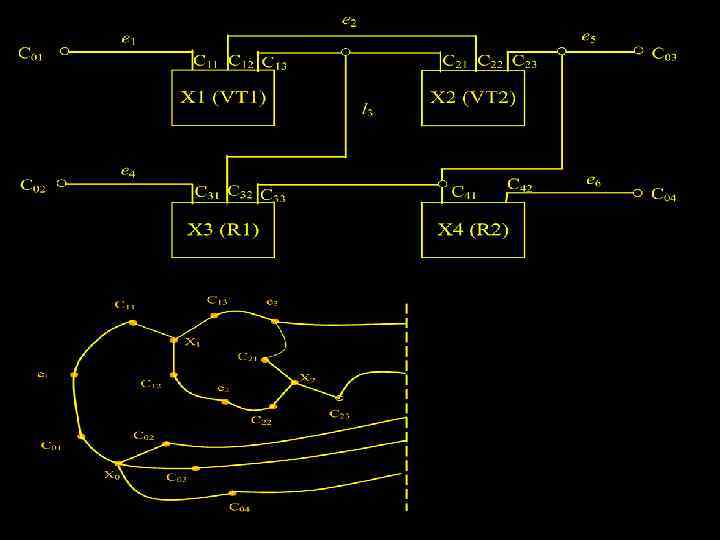
Формальное описание коммутационных схем

Формальное описание коммутационных схем

Задача 2 Практическое применение венгерского метода

Венгерский метод Пример Задана исходная матрица эффективности где Ai ‑ рабочие; Вi‑ различные виды работ. Каждый элемент матрицы соответствует тому эффекту, который может быть получен при использовании конкретного рабочего на определенном виде работ. Требуется так распределить рабочих по местам, чтобы общая эффективность их использования была max, т. е. необходимо решить задачу выбора или назначения для матрицы С.

Венгерский метод. Пример Подготовительный этап. Отыскиваем максимальные элементы в каждом из столбцов матрицы С Вычитаем каждый элемент матрицы С из максимального элемента соответствующего столбца: получаем матрицу С*

Венгерский метод. Пример Подготовительный этап. Отыскиваем минимальные элементы в каждой из строк матрицы С*: A 1 =0, А 2 = 4, А 3 = 0, А 4 = 4. Вычитаем из каждого элемента матрицы С* минимальный элемент соответствующей строки: находим матрицу Со: Операция уничтожения знака «+» над столбцом содержащим 0* условно обозначается обведением этого знака кружком

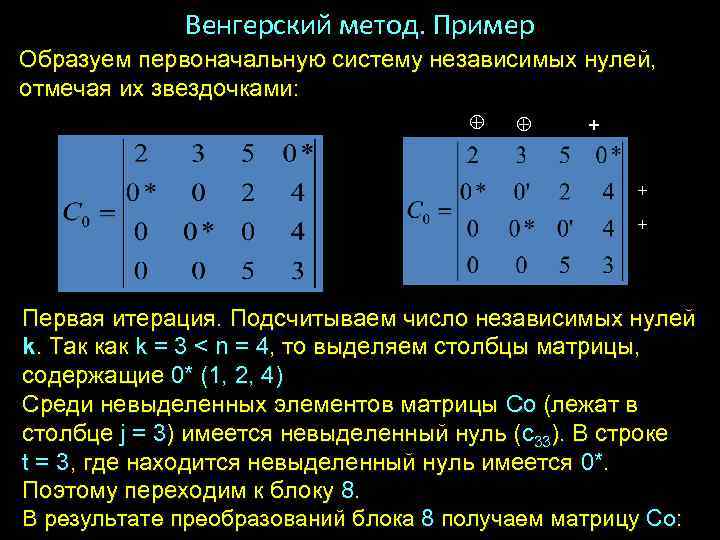Венгерский метод. Пример Образуем первоначальную систему независимых нулей, отмечая их звездочками: + + + Первая итерация. Подсчитываем число независимых нулей k. Так как k = 3 < n = 4, то выделяем столбцы матрицы, содержащие 0* (1, 2, 4) Среди невыделенных элементов матрицы Со (лежат в столбце j = 3) имеется невыделенный нуль (с33). В строке t = 3, где находится невыделенный нуль имеется 0*. Поэтому переходим к блоку 8. В результате преобразований блока 8 получаем матрицу Со:

Венгерский метод. Пример Просматриваем нули первого столбца. Нуль на месте C 31 выделять нельзя, так как он находится в ранее выделенной строке (строка помечена знаком «+» . Нуль на месте с41 можно выделить, пометив его штрихом. Так как в четвертой строке матрицы Со нет нуля со звездочкой, то выделение нулей на этом заканчивается (нет больше непомеченных столбцов, в которых можно было бы искать невыделенные нули). Получаем матрицу : + + +

Венгерский метод. Пример Построение цепочки нулей начинаем с последнего выделенного нуля со штрихом. Такой нуль находится на месте с41. От этого нуля строим дугу в том же столбце матрицы Со к нулю со звездочкой, который располагается на месте с21. От него по той же строке строим дугу цепочки до с22, далее по столбцу к нулю со звездочкой, находящимся на месте с32, а затем по строке к нулю со штрихом на месте с33. Здесь цепочка обрывается и ее построение заканчивается. В результате цепочка нулей состоит из следующей последовательности элементов матрицы

Венгерский метод. Пример Уничтожаем пометки нулей со звездочками, нули со штрихами помечаем звездочками. Убираем все пометки строк и столбцов матрицы Сo: Подсчитываем число независимых нулей (со звездочками). Так как k = 4 = n, то задача решена, т. е. получаем оптимальный план, который можно представить в виде матрицы X*:

Венгерский метод. Пример Наложив этот план на значения исходной матрицы эффективности С, получим соответствующее значение целевой функции :

Задача 3 Динамическое программирование. Поиск кратчайшего пути

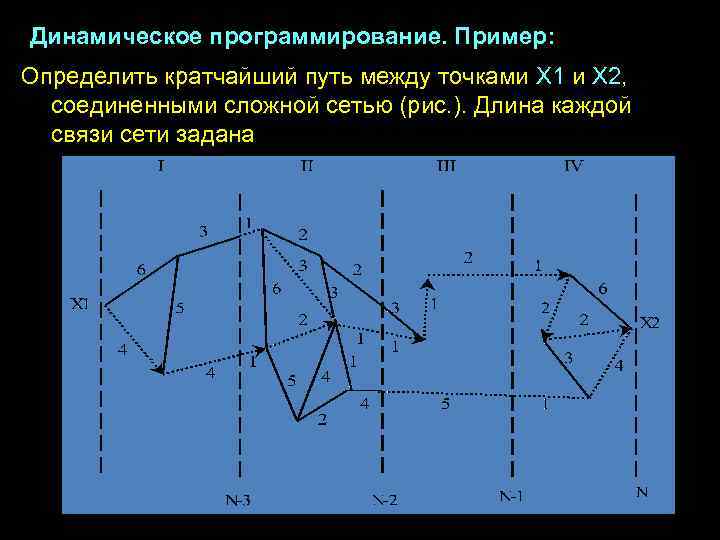Динамическое программирование. Пример: Определить кратчайший путь между точками X 1 и X 2, соединенными сложной сетью (рис. ). Длина каждой связи сети задана

Решение 1. Разобьем весь процесс поиска на этапы. 2. Сначала найдем кратчайшие пути, соединяющие точки пересечения линии N — 1 с сетью и точку Х 2 (этап IV). Таких оптимальных путей два (отмечены на рис. штрихами). 3. Определим пути между точками пересечения N-2 и N-1 с сетью, которые приводят к минимальным суммарным путям, соединяющим точки на линии N- 2 и точку Х 2 (этап III). 4. В качестве продолжения данных путей необходимо выбирать пути, найденные на IV этапе. Таких оптимальных путей – 2. 5. На этапе II находим кратчайшие пути, соединяющие точки на линии N-3 и точку Х 2. 6. Перейдя к этапу I, находим минимальный суммарный путь из точки Х 1 в Х 2, длина которого равна 21.

Решение Математически в примере решается следующее выражение: где Q – управляющий оператор, с помощью которого осуществляется последовательный переход от одного состояния в другое, f – текущее значение (приращение) целевой функции на соответствующем этапе. Из рассмотренного примера следует, что на каждом t-ом шаге перебираются не все пути, соединяющие точки на линии N-i и точку Х 2, а только оптимальные, уже отобранные на предыдущем шаге – преимущество динамического программирования. При этом эффективность рекуррентного подхода оказывается огромной в случае, когда полный перебор практически неосуществим.

Задача 4 Использование параллельного алгоритма на основе метода обратного размещения

Параллельные алгоритмы на основе метода обратного размещения Пример Задана монтажная плата и матрицы связей и длин

4. 3 Параллельные алгоритмы на основе метода обратного размещения Пример 1) Сi = 3, 2, 1, 4, 5, 6 2) Di = 1, 6, 2, 5, 3, 4 3) Размещаем 3 элемент в 1 ячейке… 3 → 1, 2 → 6, 1 → 2, 4 → 5, 5 → 3, 6 → 4.

Задача 5 Пример использования алгоритма Прима

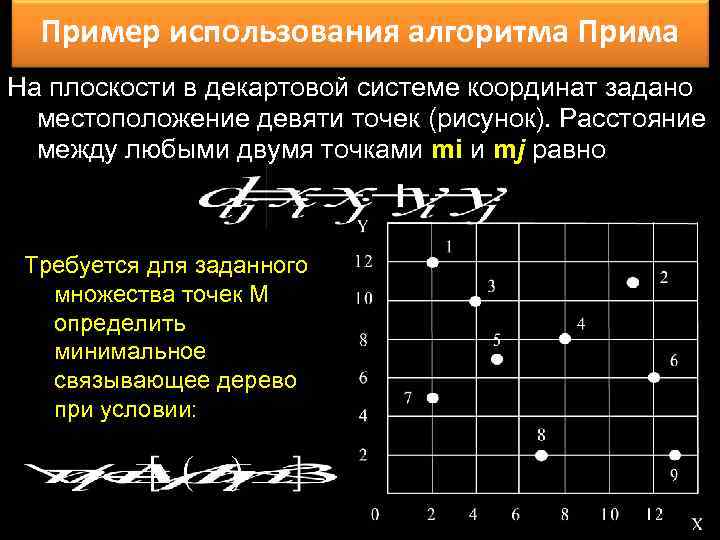Пример использования алгоритма Прима На плоскости в декартовой системе координат задано местоположение девяти точек (рисунок). Расстояние между любыми двумя точками mi и mj равно Требуется для заданного множества точек М определить минимальное связывающее дерево при условии:

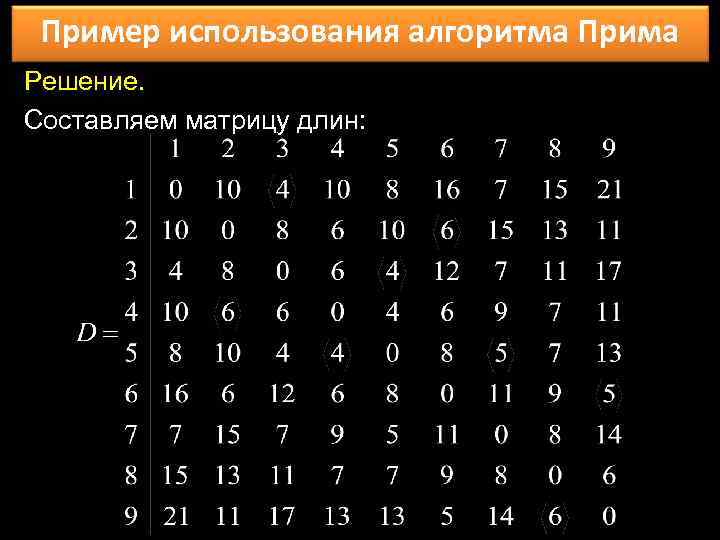Пример использования алгоритма Прима Решение. Составляем матрицу длин:

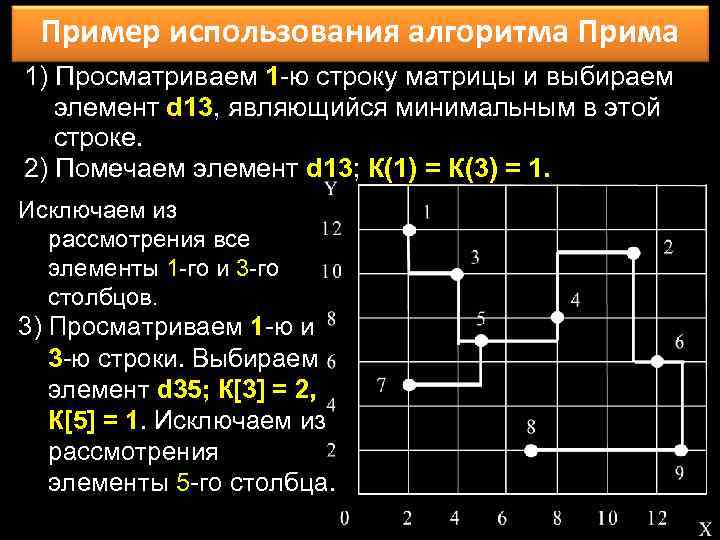Пример использования алгоритма Прима 1) Просматриваем 1 -ю строку матрицы и выбираем элемент d 13, являющийся минимальным в этой строке. 2) Помечаем элемент d 13; К(1) = К(3) = 1. Исключаем из рассмотрения все элементы 1 -го и 3 -го столбцов. 3) Просматриваем 1 -ю и 3 -ю строки. Выбираем элемент d 35; К[3] = 2, К[5] = 1. Исключаем из рассмотрения элементы 5 -го столбца.

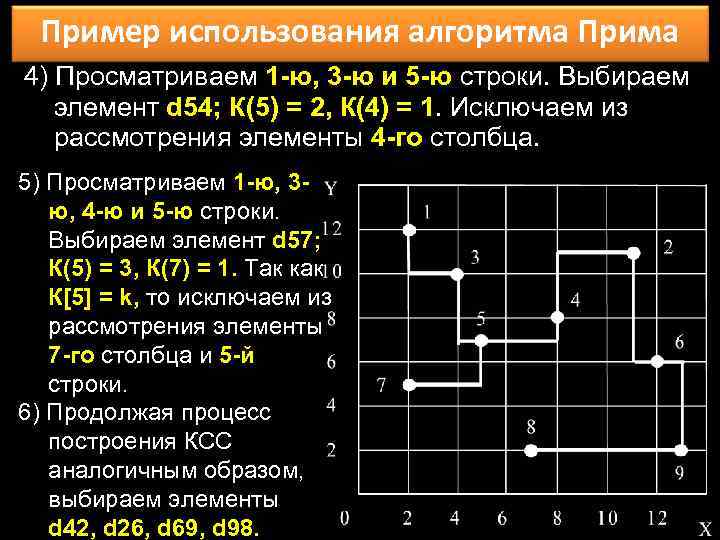Пример использования алгоритма Прима 4) Просматриваем 1 -ю, 3 -ю и 5 -ю строки. Выбираем элемент d 54; К(5) = 2, К(4) = 1. Исключаем из рассмотрения элементы 4 -го столбца. 5) Просматриваем 1 -ю, 3 ю, 4 -ю и 5 -ю строки. Выбираем элемент d 57; К(5) = 3, К(7) = 1. Так как К[5] = k, то исключаем из рассмотрения элементы 7 -го столбца и 5 -й строки. 6) Продолжая процесс построения КСС аналогичным образом, выбираем элементы d 42, d 26, d 69, d 98.

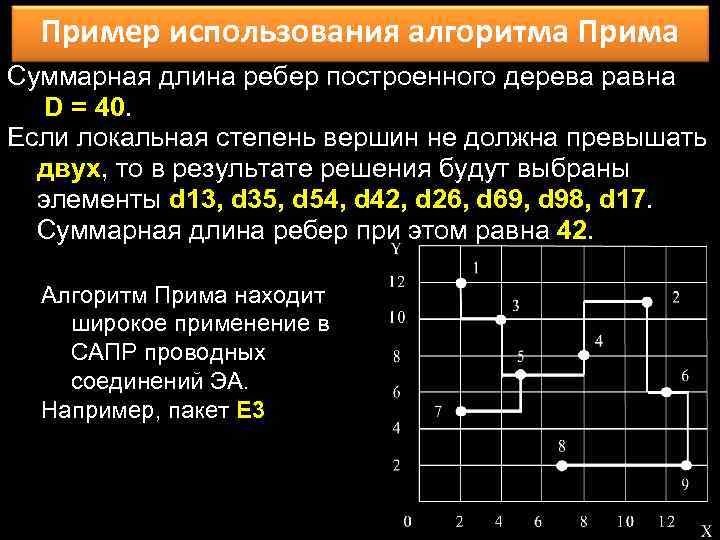Пример использования алгоритма Прима Суммарная длина ребер построенного дерева равна D = 40. Если локальная степень вершин не должна превышать двух, то в результате решения будут выбраны элементы d 13, d 35, d 54, d 42, d 26, d 69, d 98, d 17. Суммарная длина ребер при этом равна 42. Алгоритм Прима находит широкое применение в САПР проводных соединений ЭА. Например, пакет E 3

Задача 6 Примеры использования волнового алгоритма

Параллельная оптимизация пути по нескольким параметрам Например: 1) Рk = Pk-1 + 1 если в данной и соседних ячейках нет ранее построенных проводников и путевая координата не меняет своего направления; 2) Рk = Pk-1 + 2, если в соседних ячейках нет ранее построенных проводников, но путевая координата меняет свое направление; 3) Рk = Pk-1 + 5, если в данной ячейке путевая координата не меняет своего направления и нет ранее построенного проводника, но в соседней ячейке такой проводник есть; 4) Рk = Pk-1 + 8, если в данной ячейке происходит пересечение с ранее построенным проводником

Задача 7 Примеры использования модифицированных волновых алгоритмов

Задача 6 Примеры использования волнового алгоритма

Вопросы по прочитанному материалу?

Спасибо за внимание!