Информационные системы в экономике. к. т. н.

Информационные системы в экономике. к. т. н. , доцент Полупанов Дмитрий Васильевич Лекция 4. Основные понятия табличных процессоров. Применение MS Excel для решения СЛАУ и задач МОБ

Цель лекции l дать понятие табличного процессора; l рассмотреть модель решения задач средствами табличных процессоров; l изучить основные понятия табличного процессора; l рассмотреть функции MS Excel для обработки матриц и применить их для решения СЛАУ и МОБ. 2

4. 1. Понятие электронных таблиц и табличного процессора Электронные таблицы (или табличные процессоры) — это прикладные программы, предназначенные для проведения табличных расчетов и сложных расчетов по формулам. Комплекс средств, состоящий из программных модулей и реализующий некоторую совокупность операций над табличными данными, принято называть табличным процессором 3

Достоинства применения табличного процессора l Организация диалогового режима решения задачи в реальном масштабе времени (on-line), с использованием интеллектуального потенциала и опыта пользователя для получения желаемого результата; l Анализ влияния различных факторов на качество получаемого результата; l Создание наглядных графических моделей решаемых задач в виде графиков, диаграмм, гистограмм и пр. (визуализация) 4

Модель решения задачи - исходные данные - алгоритмы; - полное множество алгоритмов, входящих в табличный процессор; - полное множество допустимых значений исходных данных. 5

Наиболее популярные табличные процессоры l Microsoft Excel — программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности экономико-статистических расчетов, графические инструменты и, VBA (Visual Basic для приложений). Microsoft Excel входит в состав Microsoft Office и на сегодняшний день является одним из наиболее популярных приложений в мир l Open. Office. org Calc — табличный процессор, входящий в состав Open. Office. org. С его помощью можно анализировать вводимые данные, заниматься расчётами, прогнозировать, сводить данные с разных листов и таблиц, строить диаграммы и графики 6

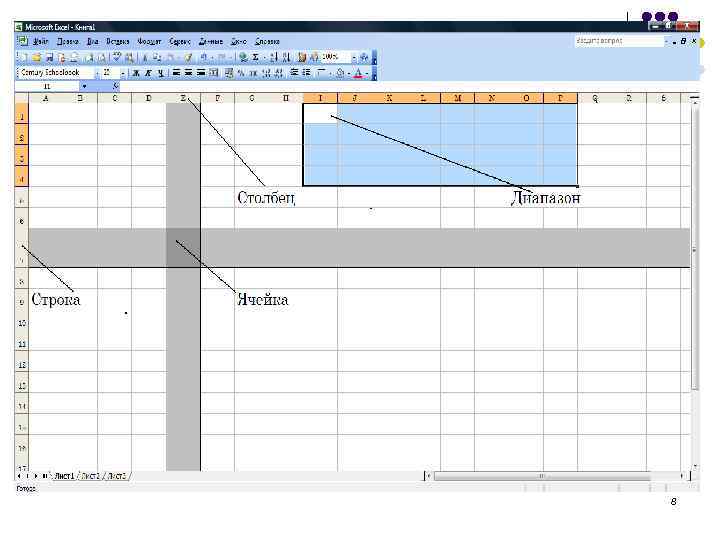
4. 2. Табличный процессор MS Excel. Основные понятия l Рабочая книга - это документ электронных таблиц, в котором объединены рабочие листы, листы диаграмм и листы макросов. Хранится в отдельном файле. l Рабочий лист - информационная структура, в которой данные упорядочены по строкам и столбцам. Рабочий лист состоит из 256 столбцов (как правило, обозначаемых латинским буквами от A до IV) и 65 356 строк. l Ячейка - наименьшая структурная единица внутри рабочего листа или листа макроса. Ячейка находится на пересечении столбца и строки. 7

8

l Область выделения - выделенный набор ячеек. Область выделения бывает смежной и несмежной. l Смежная область - это выделенная область прямоугольной формы. Порядок выделения аналогичен порядку, применяемому в редакторе Word. l Несмежная область - это область выделения, состоящая из нескольких областей прямоугольной формы. Выделяют первую смежную область. Далее держат нажатой клавишу «Ctrl» и выделяют остальные смежные области. l Диапазон - адрес области выделения. Для смежной (т. е. прямоугольной) области диапазон имеет вид: адрес ячейки из левого верхнего угла, символ «двоеточие» , адрес ячейки из правого нижнего угла. Например, A 1: B 5. Для несмежных областей диапазон состоит из списка диапазон смежных областей, разделенных символом «точка с запятой» . 9

Содержимое ячейки l число в десятичной и нормальной форме, процентном, денежном и финансовом формате; l текст; l формула; l дата, время; l комментарий (начинается с символа «апостроф» ). 10

Адрес ячейки l Адрес ячейки - используется для ссылки на содержимое ячейки. Состоит из буквы столбца ячейки и номера строки. Например, А 5 или В 7. С помощью адреса можно найти любую ячейку в рабочей книге. l Имя - Отдельной ячейке или диапазону ячеек можно присваивать имена. Далее эти имена можно использовать вместо адресов ячеек. При переносе именованной ячейки имя также переносится 11

Ссылки на ячейки l Зависимая ячейка - это ячейка, l Ссылка указывает на ячейку или формула в которой ссылается диапазон ячеек листа и на содержимое другой передает в Microsoft Excel влияющей ячейки. Если сведения о расположении изменится содержимое значений или данных, которые влияющей ячейки, то изменится требуется использовать в и зависимая ячейка. формуле. При помощи ссылок l Влияющая ячейка - это ячейка, можно использовать в одной ссылка на которую содержится в формуле данные, находящиеся формуле в другой ячейке. в разных частях листа, а также использовать в нескольких l Ссылка - основной элемент при формулах значение одной выполнении вычислений с ячейки. Кроме того, можно использованием нескольких задавать ссылки на ячейки ячеек. Основным элементом других листов той же книги и на ссылки является адрес ячейки. другие книги. Ссылки на ячейки Существует абсолютная и других книг называются связями. относительная ссылки на ячейку 12

ü Относительная ссылка в формуле, например A 1, основана на относительной позиции ячейки, содержащей формулу, и ячейку, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании относительной ссылки из ячейки B 2 в ячейку B 3, она автоматически изменяется с =A 1 на =A 2. ü Абсолютная ссылка ячейки в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании формулы вдоль строк и вдоль столбцов абсолютная ссылка не корректируется. Например, при копировании абсолютной ссылки из ячейки B 2 в ячейку B 3, она остается прежней =$A$1. ü Смешанная ссылка содержит либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка столбцов приобретает вид $A 1, абсолютная ссылка строки приобретает вид A$1. При изменении позиции ячейки, содержащей формулу, относительная ссылка изменяется, а абсолютная ссылка не изменяется. Например, при копировании смешанной ссылки из ячейки A 2 в ячейку B 3, она изменяется с =A$1 на =B$1. 13

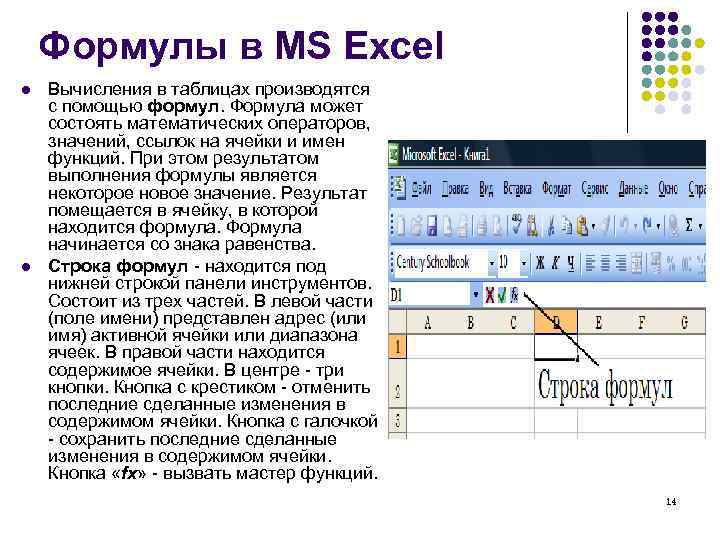Формулы в MS Excel l Вычисления в таблицах производятся с помощью формул. Формула может состоять математических операторов, значений, ссылок на ячейки и имен функций. При этом результатом выполнения формулы является некоторое новое значение. Результат помещается в ячейку, в которой находится формула. Формула начинается со знака равенства. l Строка формул - находится под нижней строкой панели инструментов. Состоит из трех частей. В левой части (поле имени) представлен адрес (или имя) активной ячейки или диапазона ячеек. В правой части находится содержимое ячейки. В центре - три кнопки. Кнопка с крестиком - отменить последние сделанные изменения в содержимом ячейки. Кнопка с галочкой - сохранить последние сделанные изменения в содержимом ячейки. Кнопка «fx» - вызвать мастер функций. 14

Возможные ошибки при использовании формул l ДЕЛ/0! – деление на ноль l #ИМЯ? - неопределенное имя ячейки l #ЗНАЧ! – действия над текстом, а не числом l #ССЫЛКА – ссылка на несуществующую ячейку l #Н/Д – неопределенные данные l #ЧИСЛО! – некорректная математическая операция 15

4. 2. Функции в MS Excel l Функция - объединение нескольких математических операций для решения определенной задачи. Функции представляют собой формулы, имеющие один или несколько аргументов. 16

Применение табличного процессора для решения СЛАУ 17

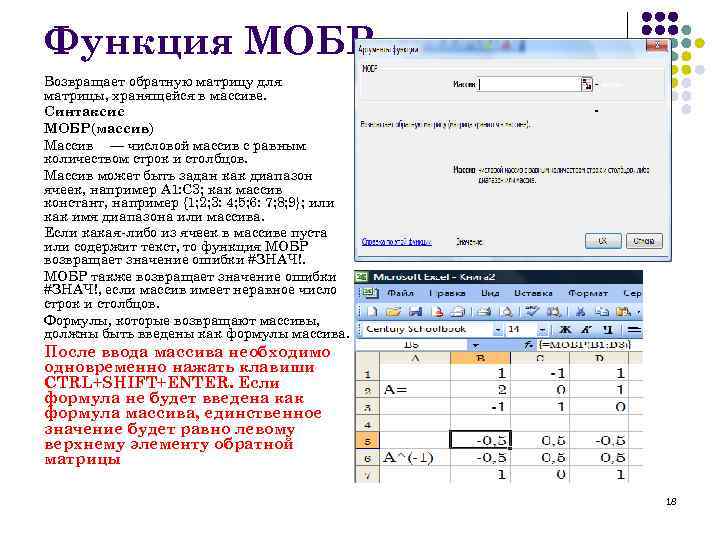Функция МОБР Возвращает обратную матрицу для матрицы, хранящейся в массиве. Синтаксис МОБР(массив) Массив — числовой массив с равным количеством строк и столбцов. Массив может быть задан как диапазон ячеек, например A 1: C 3; как массив констант, например {1; 2; 3: 4; 5; 6: 7; 8; 9}; или как имя диапазона или массива. Если какая-либо из ячеек в массиве пуста или содержит текст, то функция МОБР возвращает значение ошибки #ЗНАЧ!. МОБР также возвращает значение ошибки #ЗНАЧ!, если массив имеет неравное число строк и столбцов. Формулы, которые возвращают массивы, должны быть введены как формулы массива. После ввода массива необходимо одновременно нажать клавиши CTRL+SHIFT+ENTER. Если формула не будет введена как формула массива, единственное значение будет равно левому верхнему элементу обратной матрицы 18

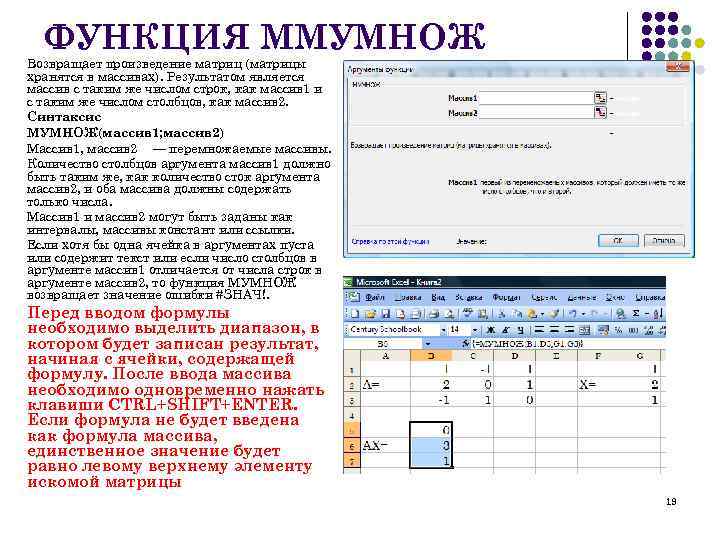ФУНКЦИЯ ММУМНОЖ Возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив 1 и с таким же числом столбцов, как массив 2. Синтаксис МУМНОЖ(массив 1; массив 2) Массив 1, массив 2 — перемножаемые массивы. Количество столбцов аргумента массив 1 должно быть таким же, как количество сток аргумента массив 2, и оба массива должны содержать только числа. Массив 1 и массив 2 могут быть заданы как интервалы, массивы констант или ссылки. Если хотя бы одна ячейка в аргументах пуста или содержит текст или если число столбцов в аргументе массив 1 отличается от числа строк в аргументе массив 2, то функция МУМНОЖ возвращает значение ошибки #ЗНАЧ!. Перед вводом формулы необходимо выделить диапазон, в котором будет записан результат, начиная с ячейки, содержащей формулу. После ввода массива необходимо одновременно нажать клавиши CTRL+SHIFT+ENTER. Если формула не будет введена как формула массива, единственное значение будет равно левому верхнему элементу искомой матрицы 19

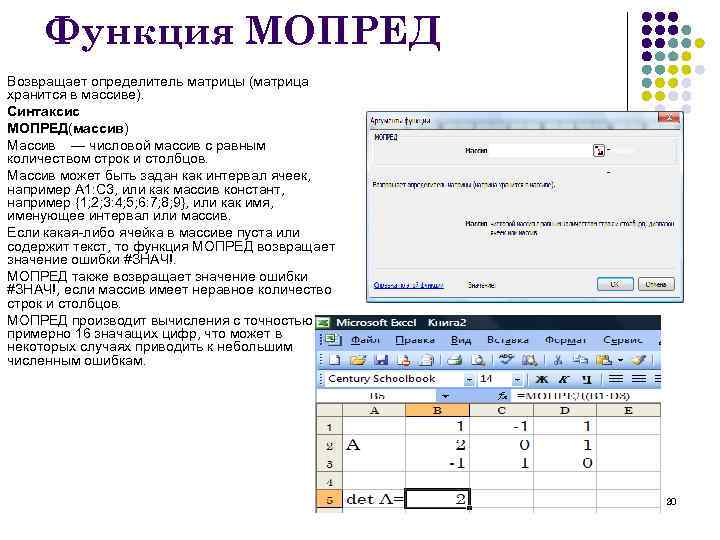Функция МОПРЕД Возвращает определитель матрицы (матрица хранится в массиве). Синтаксис МОПРЕД(массив) Массив — числовой массив с равным количеством строк и столбцов. Массив может быть задан как интервал ячеек, например A 1: C 3, или как массив констант, например {1; 2; 3: 4; 5; 6: 7; 8; 9}, или как имя, именующее интервал или массив. Если какая-либо ячейка в массиве пуста или содержит текст, то функция МОПРЕД возвращает значение ошибки #ЗНАЧ!. МОПРЕД также возвращает значение ошибки #ЗНАЧ!, если массив имеет неравное количество строк и столбцов. МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к небольшим численным ошибкам. 20

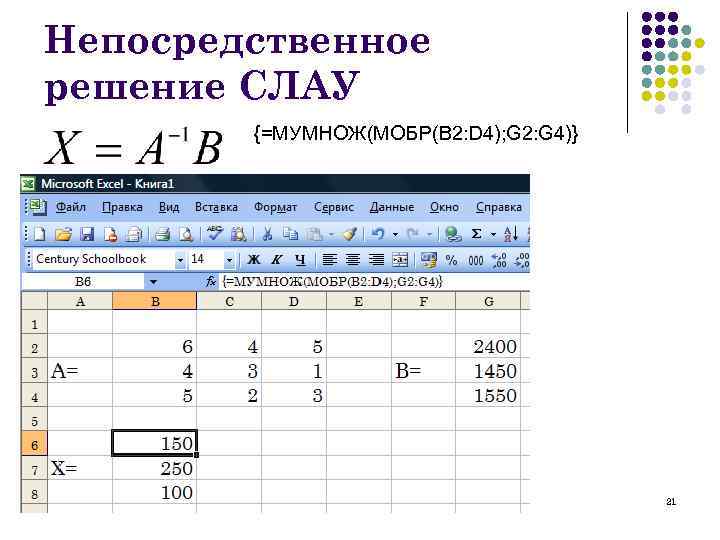Непосредственное решение СЛАУ {=МУМНОЖ(МОБР(B 2: D 4); G 2: G 4)} 21

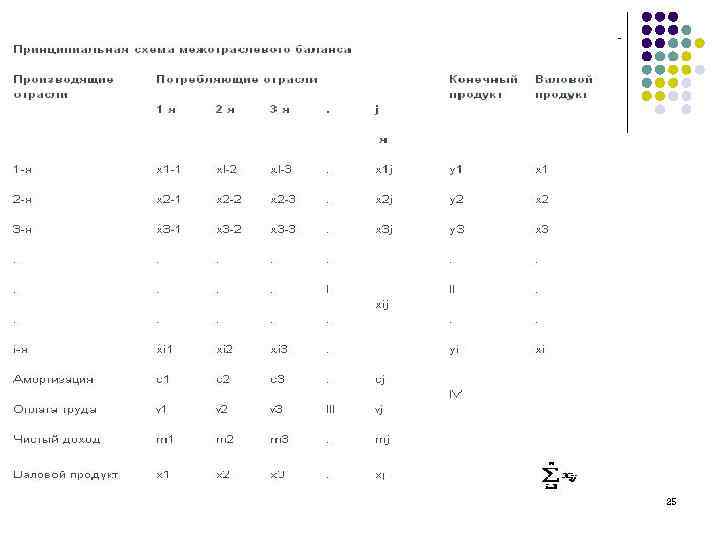
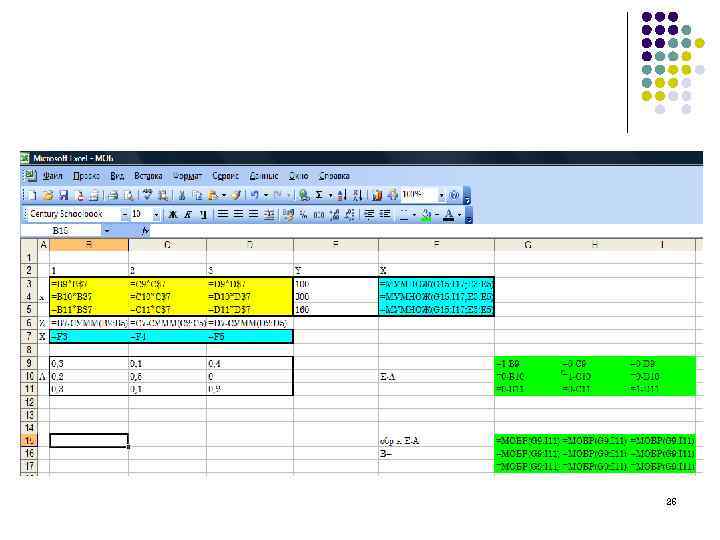
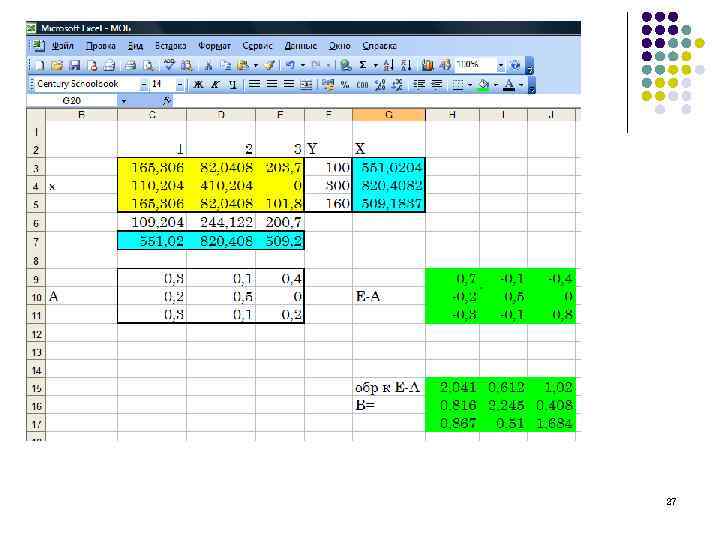
Использование средств табличного процессора для решения макроэкономических задач l Межотраслевой баланс (МОБ, метод «затраты-выпуск» ) — экономико- математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. l Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли. l В Модели МОБ выделяются четыре квадранта. В первом отражается промежуточное потребление и система производственных связей, во втором — структура конечного использования ВВП, в третьем — стоимостная структура ВВП, а в четвёртом — перераспределение национального дохода 22

Модель межотраслевого баланса - величина межотраслевых потоков продукции; - конечный продукт; - условно чистая продукция отрасли; - валовый продукт 23

Модель «затраты-выпуск» - коэффициент прямых материальных затрат; - Модель В. В. Леонтьева «затраты-выпуск» 24

25

26

27