Информационнологические основы представления информации в ЭВМ Учебные вопросы

Информационнологические основы представления информации в ЭВМ Учебные вопросы 1. Системы счисления и формы представления чисел (двоичное кодирование) 2. Основы алгебры логики 1

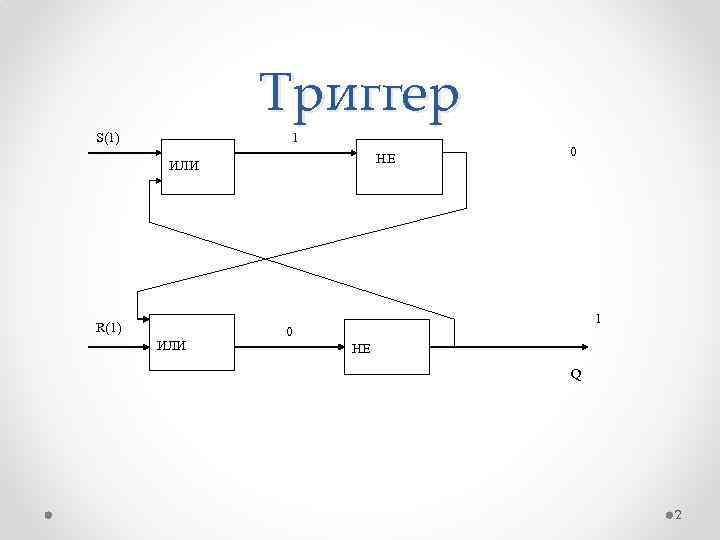
Триггер S(1) 1 R(1) ИЛИ 0 НЕ ИЛИ 0 1 НЕ Q 2

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе Десятичная СС является позиционной. На рисунке слева значение цифры 9 изменяется в зависимости от ее положения в числе. Первая слева девятка делает вклад в общее значение десятичного числа 900 единиц, вторая — 90, а третья — 9 единиц. 3

Римская система счисления является непозиционной Значение цифры Х в числе ХХI остается неизменным при вариации ее положения в числе. 4

Примеры систем счисления (15)10; (1011)2; (735)8; (1 EA 9 F)16. Иногда скобки опускают и оставляют только индекс: 1510; 10112; 7358; 1 EA 9 F 16. Есть еще один способ обозначения СС: при помощи латинских букв, добавляемых после числа. Например, 15 D; 1011 B; 735 Q; 1 EA 9 FH. 5

Чем больше основание системы счисления, тем компактнее запись числа. Так двоичное изображение числа требует примерно в 3, 3 раза большего количества цифр, чем его десятичное представление. Рассмотрим два числа: 97 D = 1100001 B. Двоичное представление числа имеет заметно большее количество цифр. 6

В СС с основанием Q используются цифры от 0 до Q – 1. где в качестве коэффициентов ai могут стоять любые цифры, используемые в данной СС. 7

Пример Перевести число 11011. 11 В из двоичной СС в десятичную СС. Решение. (11011. 11)2 = 1× 24 + 1× 23 + 0× 22 + 1× 21 + 1× 20 + 1× 2 -1 + 1× 2 -2 = = 16 + 8 + 0 + 2 + 1 + 0. 5 + 0. 25 = (27. 75)10 8

Пример Перевести целое десятичное число 37 D в двоичную СС: Решение. Результат перевода: (37)10 = (100101)2. 9

Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых (т. е. к ним возможно обращение) ячейках памяти. Очевидно, адресом числа следует считать адрес первого байта. В байте может содержаться произвольный код из восьми двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число. 1 0 0 1 10

Целые числа. Целые положительные числа от 0 до 255 можно представить непосредственно в двоичной системе счисления (двоичном коде). Такие числа будут занимать один байт в памяти компьютера. Число Двоичный код числа 0 0000 1 0000 0001 2 0000 0010 3 0000 0011 … … 255 1111 11

Если нужны и отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит; ноль интерпретируется как плюс, единица как минус. В таком случае одним байтом может быть закодированы целые числа в интервале от – 127 до +127, причем двоичная арифметика будет несколько усложнена, так как в этом случае существуют два кода, изображающих число ноль 0000 и 1000 0000, и в компьютерах на аппаратном уровне это потребуется предусмотреть. 12

Дополнительный код В дополнительном коде положительные числа совпадают с положительными числами в прямом коде, отрицательные же числа получаются в результате вычитания из 1 0000 соответствующего положительного числа. Например, число – 3 получит код 1 0000 0011 1111 1101 13

В дополнительном коде хорошо реализуется арифметика, так каждый последующий код получается из предыдущего прибавлением единицы с точностью до бита в девятом разряде. Например, 5– 3 = 5 + (– 3). 0000 0101 1111 1101 1 0000 0010, т. е. , отбрасывая подчеркнутый старший разряд, получим 2. 14

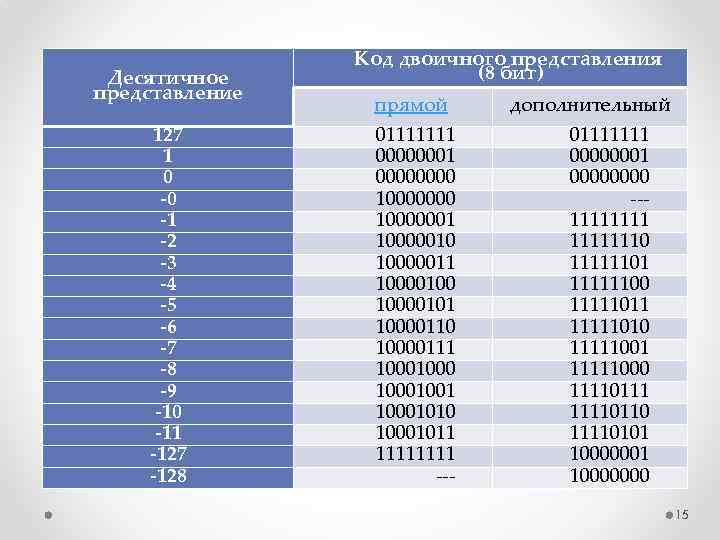
Десятичное представление 127 1 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -127 -128 Код двоичного представления (8 бит) прямой дополнительный 01111111 00000001 00000000 10000000 --- 10000001 1111 10000010 11111110 10000011 11111101 10000100 11111100 10000101 11111011 10000110 11111010 10000111 11111001 1000 11111000 10001001 11110111 10001010 11110110 10001011 11110101 1111 10000001 --- 10000000 15

Чтобы произвести сложение с отрицательным значением чисел надо: 1) перевести числа в дополнительный код Положительное число – тоже самое, Отрицательное число – в дополнительном коде равно 10000 – значение отрицательного числа. 2) произвести сложение дополнительных кодов, получим результат в дополнительном коде. Если сумма меньше 10000000, то число отрицательное, если больше – положительное. 3) перевести сумму в прямой код: Вычтем из большего (между полученной суммой и 10000) меньшее, это будет значение числа, а знак «+» - если сумма больше, «-» - если сумма меньше. 16

Представление действительных чисел N = M*np , где N — записываемое число; M — мантисса; n — основание показательной функции; p (целое) — порядок; Например: 1 000 (один миллион): ; N = 1 000, M = 1, 0, n = 10, p = 6. 17

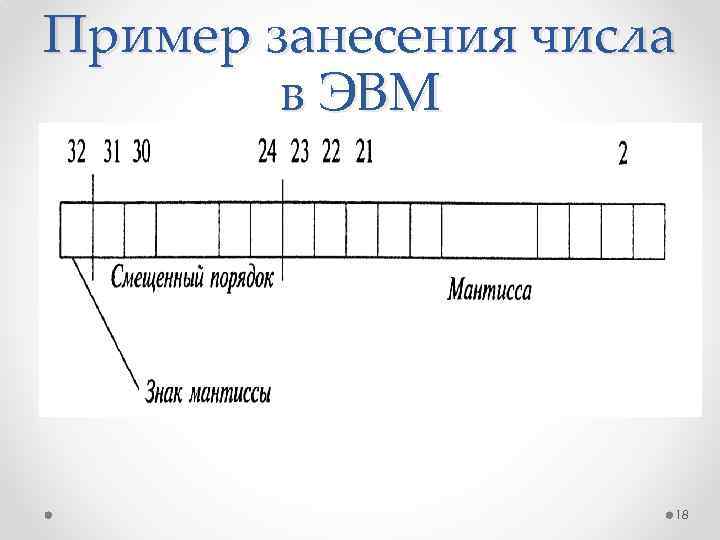
Пример занесения числа в ЭВМ 18

Порядок числа может быть как положительным, так и отрицательным. Чтобы отразить это в двоичной форме, величина порядка представляется в виде суммы истинного порядка и константы, равной абсолютной величине максимального по модулю отрицательного порядка, называемой смещением. Например, если порядок может принимать значения от – 128 до 127 (8 бит), тогда, выбрав в качестве смещения 128, можно представить диапазон значений порядка от 0 (– 128+128, порядок + смещение) до 255 (127+128). 19

Основы алгебры логики Для анализа и синтеза схем в ЭВМ при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики. Алгебра логики - это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями. 20

Высказывание - это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т. е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным. 21

В алгебре логики все высказывания обозначают буквами а, b, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры. 22

1. Логическое умножение (конъюнкция) Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания. В русском языке операция конъюнкции выражается союзом «и» . 23

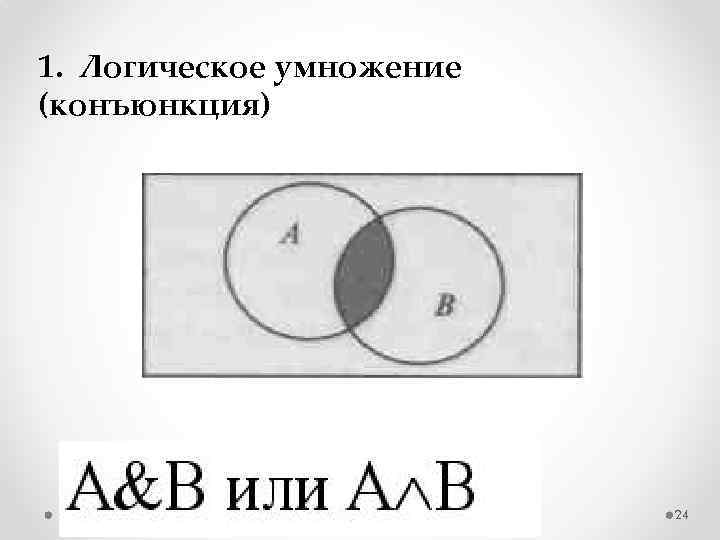
1. Логическое умножение (конъюнкция) 24

2. Логическое сложение (дизъюнкция) Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний. В русском языке операция дизъюнкции выражается союзом «или» . 25

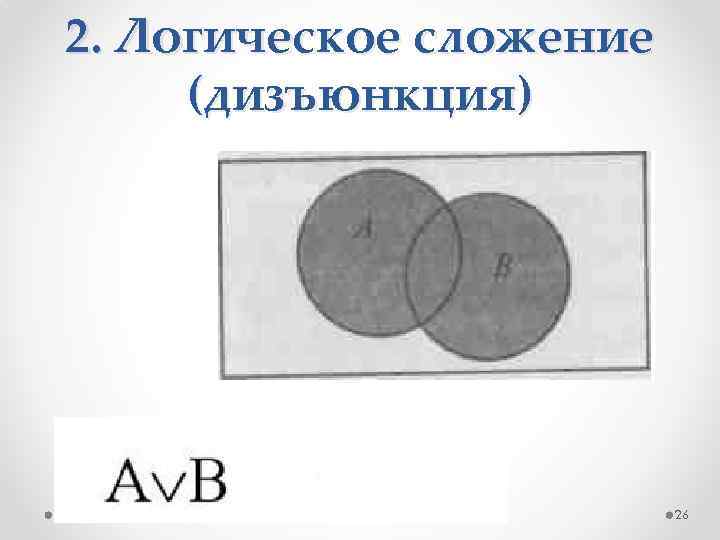
2. Логическое сложение (дизъюнкция) 26

3. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным. В русском языке операция инверсии образуется присоединением частицы «не» к высказыванию. 27

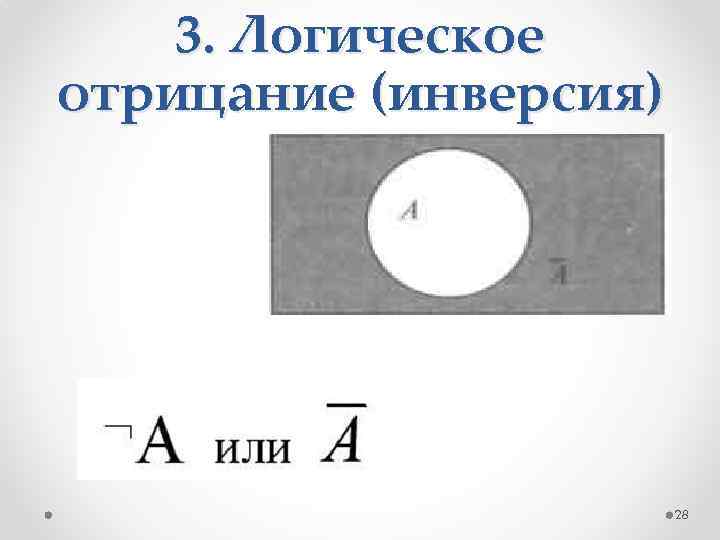
3. Логическое отрицание (инверсия) 28

4. Логическое следование (импликация) Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание). В русском языке операция импликации выражается оборотом речи «если…, то…» . 29

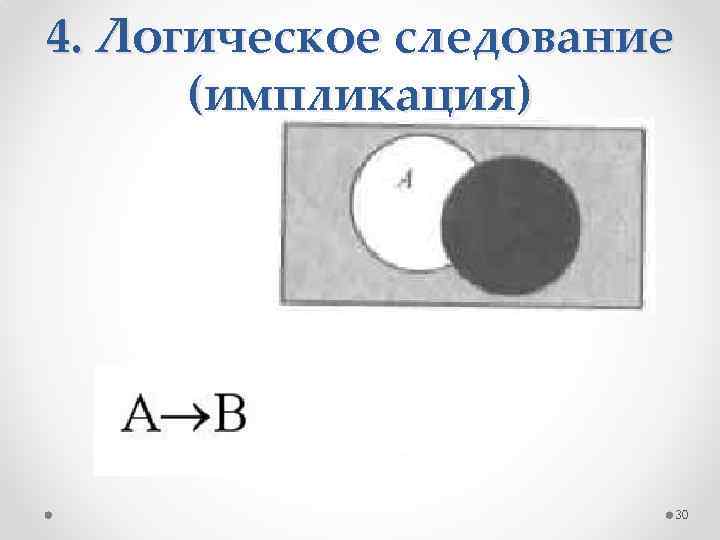
4. Логическое следование (импликация) 30

5. Логическое равенство (эквивалентность) Составное высказывание, образованное с помощью операции логического равенства (эквивалентности), истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. В русском языке операция эквивалентности выражается оборотом речи «…тогда и только тогда, когда…» . 31

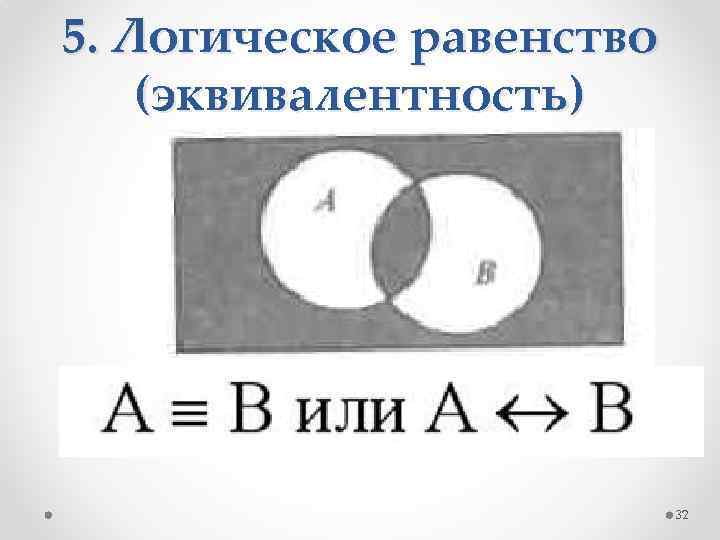
5. Логическое равенство (эквивалентность) 32

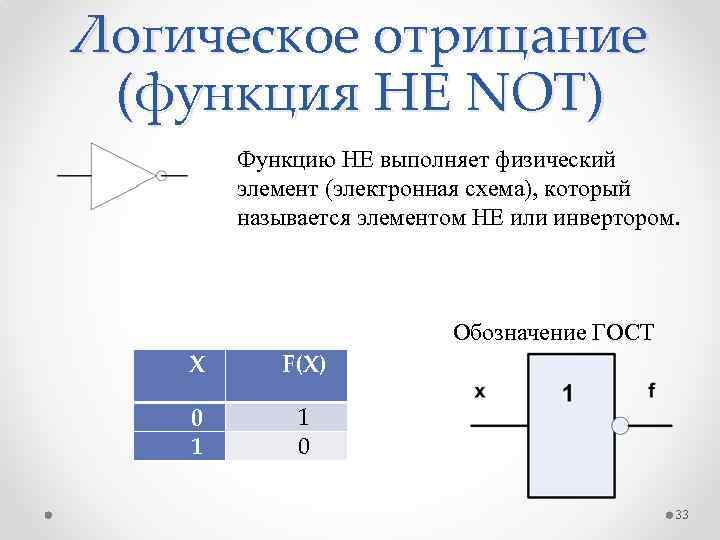
Логическое отрицание (функция НЕ NOT) Функцию НЕ выполняет физический элемент (электронная схема), который называется элементом НЕ или инвертором. Обозначение ГОСТ X F(X) 0 1 1 0 33

Логическое умножение (конъюнкция И AND) Функция «И» выполняется электронной схемой, которая называется элементом «И» или коньюнктором. ЛФ конъюнкция обозначается X 1 X 2 F(X 1, X 2) 0 0 1 1 в виде: f=x 1*x 2 и читается: «f есть (эквивалентно) х1 и x 2» . 1 Обозначение по ГОСТ 34

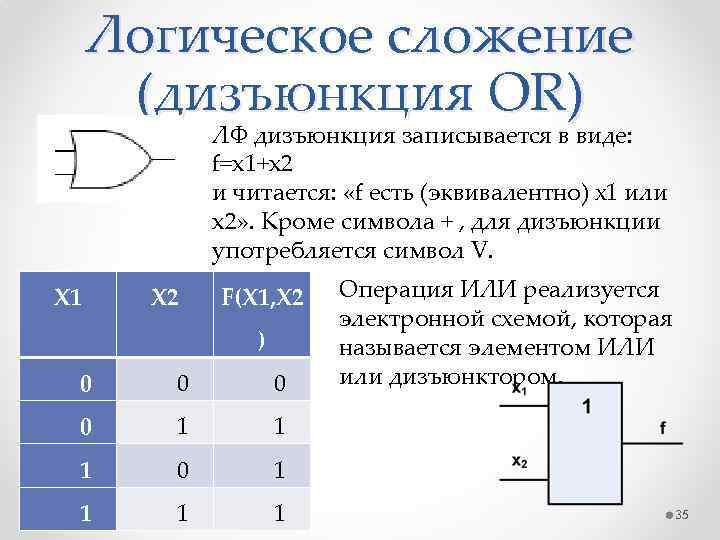
Логическое сложение (дизъюнкция OR) ЛФ дизъюнкция записывается в виде: f=x 1+x 2 и читается: «f есть (эквивалентно) х1 или x 2» . Кроме символа + , для дизъюнкции употребляется символ V. X 1 X 2 F(X 1, X 2 ) 0 0 1 1 1 0 1 1 Операция ИЛИ реализуется электронной схемой, которая называется элементом ИЛИ или дизъюнктором. 35

ЕН — И яицареп ( о о ) ) Отрицание конъюнкции Функцию И — НЕ выполняет схема, которая называется элементом И — НЕ. X 1 X 2 F(X 1, X 2 ) 0 0 1 1 1 0 36

)ЕН — ИЛИ яицарепо ( ( Отрицание дизъюнкции Операцию ИЛИ — НЕ выполняет электронный элемент, который называется элементом ИЛИ — НЕ. X 1 X 2 F(X 1, X 2) 0 0 1 0 1 0 0 1 1 0 Обозначение элемента ИЛИ — НЕ на функциональных схемах 37

ИСКЛЮЧАЮЩЕЕ ИЛИ (операция НЕРАВНОЗНАЧНОСТЬ или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА XOR ). X 1 X 2 F(X 1, X 2) 0 0 1 1 1 0 38

Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ (РАВНОЗНАЧНОСТЬ) X 1 X 2 F(X 1, X 2) 0 0 1 0 1 0 0 1 1 1 39