Инерциальные навигационные системы 1 Назначение инерциальных навигационных

Инерциальные навигационные системы 1

Назначение инерциальных навигационных систем Инерциальные навигационные системы (ИНС) – это технические средства, которые позволяют определять непосредственно на движущемся объекте его координаты и вектор путевой скорости в результате измерения и интегрирования ускорений, действующих на объект во время движения. Ускорения измеряются в инерциальной системе координат – неподвижной или движущейся прямолинейно и равномерно. Инерциальная система пригодна для навигации в любой части земного шара, в любое время и в любую погоду. ИНС не подвержена внешним помехам и не имеет ограничений по дальности и высоте полета. Система обладает всеми преимуществами автономного средства самолетовождения (не демаскирует движущийся объект, не зависит от видимости земной поверхности, небесной сферы и т. п. ). Система пригодна как для дальней так и для ближней навигации, т. е. в принципе для всех летательных аппаратов, наземных средств передвижения, надводного и подводного флота. 2

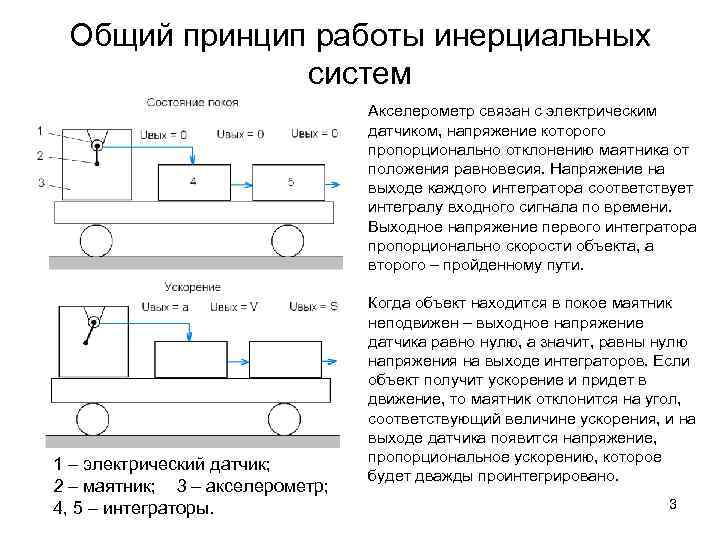Общий принцип работы инерциальных систем Акселерометр связан с электрическим датчиком, напряжение которого пропорционально отклонению маятника от положения равновесия. Напряжение на выходе каждого интегратора соответствует интегралу входного сигнала по времени. Выходное напряжение первого интегратора пропорционально скорости объекта, а второго – пройденному пути. 1 – электрический датчик; 2 – маятник; 3 – акселерометр; 4, 5 – интеграторы. Когда объект находится в покое маятник неподвижен – выходное напряжение датчика равно нулю, а значит, равны нулю напряжения на выходе интеграторов. Если объект получит ускорение и придет в движение, то маятник отклонится на угол, соответствующий величине ускорения, и на выходе датчика появится напряжение, пропорциональное ускорению, которое будет дважды проинтегрировано. 3

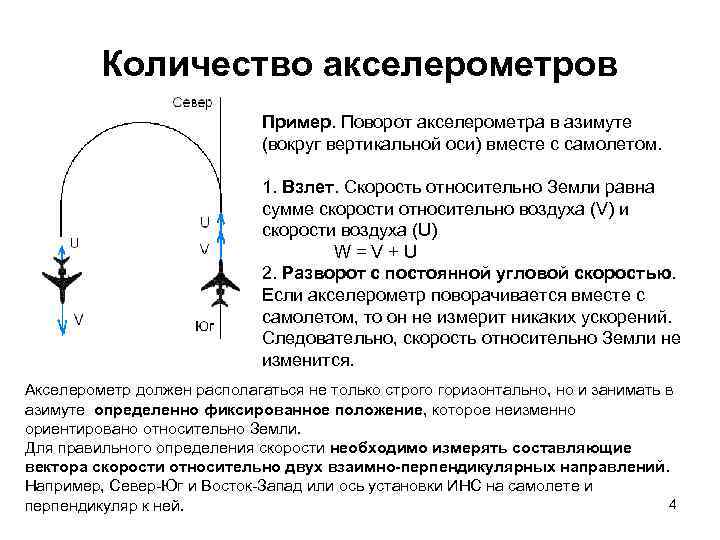Количество акселерометров Пример. Поворот акселерометра в азимуте (вокруг вертикальной оси) вместе с самолетом. 1. Взлет. Скорость относительно Земли равна сумме скорости относительно воздуха (V) и скорости воздуха (U) W=V+U 2. Разворот с постоянной угловой скоростью. Если акселерометр поворачивается вместе с самолетом, то он не измерит никаких ускорений. Следовательно, скорость относительно Земли не изменится. Акселерометр должен располагаться не только строго горизонтально, но и занимать в азимуте определенно фиксированное положение, которое неизменно ориентировано относительно Земли. Для правильного определения скорости необходимо измерять составляющие вектора скорости относительно двух взаимно-перпендикулярных направлений. Например, Север-Юг и Восток-Запад или ось установки ИНС на самолете и 4 перпендикуляр к ней.

Определение скорости с помощью двух акселерометров с фиксированным положением в азимуте 1. Взлет. Первый акселерометр определяет скорость в направлении Север. Юг (WN), второй – Восток-Запад (WE) WN = V + U WE = 0 2. Разворот с постоянной угловой скоростью. Первый акселерометр начинает измерять составляющую центростремительного ускорения VωSinωt, второй – VωCosωt WN = V + U – ∫VωSinωtdt WE = – ∫VωCosωtdt 3. Окончание разворота. Время разворота на 180° равно π/ω, поэтому интегрирование выполняется на интервале от 0 до π/ω | WN = V + U – VωCosωt / ω π/ω÷ 0 = V + U – V(Cos π – Cos 0) = V + U – 2 V = U – V WE = – VωSinωt / ω |π/ω÷ 0 = – V(Sin π – Sin 0) = 0 После разворота интеграторы покажут, что скорость в направлении Север-Юг равна U – V, а в направлении Восток-Запад – равна нулю. Аналогично, в процессе разворота геометрическая сумма интегралов показаний акселерометров будет равна действительной скорости самолета. 5

Расположение акселерометров на самолете Пример. Акселерометр установлен таким образом, что измеряет ускорение по продольной оси самолета. Наличие угла атаки приводит к измерению ускорения, равного g. Sin. A, хотя в действительности самолет летит с постоянной скоростью V. Для правильного измерения ускорения акселерометр должен независимо от эволюций самолета оставаться строго в горизонтальном положении – определять только горизонтальные ускорения. Задача определения вертикали на движущемся объекте достаточно сложна. Уровни и нивелиры дают «кажущуюся» вертикаль, направленную по равнодействующей силы тяжести и сил инерции от ускорений, действующих на объект. Такая вертикаль сильно возмущаема и непригодна для применения в ИНС. Например, постоянный наклон платформы с акселерометром по отношению к горизонту (невыдерживание вертикали) на угол в 1 миллирадиан (3, 4') приводит к ошибке (за счет интегрирования составляющей ускорения силы тяжести в 0, 001 g≈0, 01 м/сек 2) примерно в 65 км за 1 час полета. Ошибка определения пройденного пути из-за погрешности измерения ускорения растет в этом случае пропорционально квадрату времени действия системы. 6

Горизонтальная стабилизация акселерометров При перемещении самолета из точки А направлением вертикали АО в точку В с направлением вертикали ВО истинная вертикаль повернется на угол β. Для того чтобы платформа в точке В заняла горизонтальное положение, ее необходимо повернуть относительно первоначального положения АО на угол β. Это обеспечит непрерывную стабилизацию платформы в плоскости горизонта. Для решения задачи построения вертикали, необходимо в любой момент времени знать величину угла β и поворачивать платформу на этот угол. Величину угла β можно получить, измеряя расстояние S и деля его на радиус Земли: β = S/Rз. Для правильного поворота платформы надо сохранить направление АО, взятое в момент старта, и от него поворачивать платформу на угол β. Сохранение направления АО может быть осуществлено с помощью гироскопов. 7

Принцип построения вертикали Поместим в точке А платформу с акселерометром и гироскоп, способный удерживать заданное ему направление в пространстве (например, направление АО). Так как процесс построения вертикали должен быть непрерывным, то Δγ = Δβ = ΔS/Rз или dγ/dt = dβ/dt = d. S /dt /Rз d. S /dt = ∫adt значит γ’ = 1/Rз ∫adt Результат определяет устойчивую вертикаль. Если нормаль к платформе отклонится от истинной вертикали на малый угол γ 0, то акселерометр измерит составляющую земного ускорения a = -g. Sinγ 0. Ввиду малости значений угла γ 0 можно считать Sinγ 0≈γ 0, тогда a = -gγ 0 и γ’ 0 = -g/Rз ∫γ 0 dt или γ’’ 0 + γ 0 g/Rз = 0. Это уравнение описывает незатухающие колебания системы (маятника) относительно истинной вертикали места. Период колебаний вычисляется как 8

Маятник Шулера Получен период так называемого маятника Шулера. Такой маятник при движении его точки подвеса вокруг поверхности Земли всегда поворачивается на тот же угол, что и вертикаль. Маятник Шулера это идеальное устройство, которое находится в равновесии, каковы бы ни были движения его точки подвеса. Вертикаль в виде маятника с периодом колебаний 84, 4 мин реально создать невозможно. Период колебаний физического маятника массы m, моментом инерции J 0 и плечом L Для периода 84. 4 мин необходимо, чтобы плечо было равно нескольким тысячам километров или нескольким микронам. Ни то, ни другое в маятниковой вертикали реализовано быть не может. Условие невозмущаемости устройства, моделирующего маятник Шулера, состоит в том, что угловое ускорение платформы с акселерометрами должно быть равно угловому ускорению поворота вертикали (угловому ускорению самолета относительно центра Земли). 9

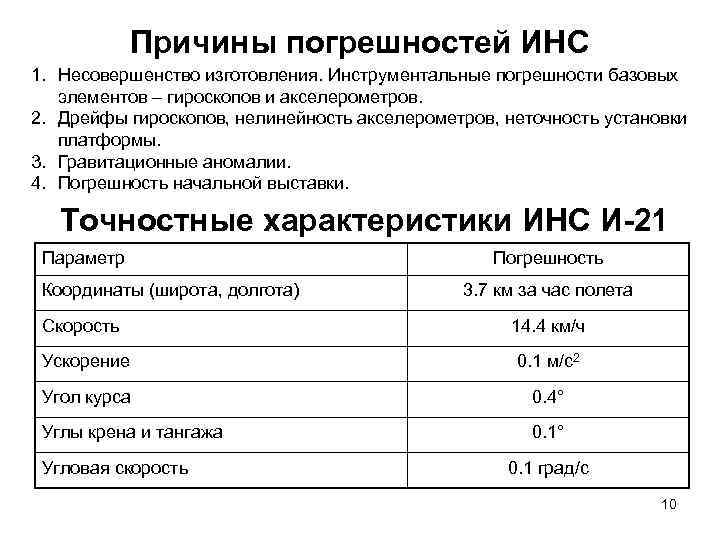Причины погрешностей ИНС 1. Несовершенство изготовления. Инструментальные погрешности базовых элементов – гироскопов и акселерометров. 2. Дрейфы гироскопов, нелинейность акселерометров, неточность установки платформы. 3. Гравитационные аномалии. 4. Погрешность начальной выставки. Точностные характеристики ИНС И-21 Параметр Координаты (широта, долгота) Скорость Погрешность 3. 7 км за час полета 14. 4 км/ч Ускорение 0. 1 м/с2 Угол курса 0. 4° Углы крена и тангажа 0. 1° Угловая скорость 0. 1 град/с 10