Industrial Strength SAT-based Alignability Algorithm for Hardware Equivalence

Industrial Strength SAT-based Alignability Algorithm for Hardware Equivalence Verification Daher Kaiss, Marcelo Skaba, Ziyad Hanna, Zurab Khasidashvili Formal Technologies Group Intel, Israel Design Center, Haifa

Purpose • Sequential Equivalence Verification (SEV) as a productivity boost in hardware design • A novel method for automatic initialization of hardware design 2

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 3

Problem Statement • Traditional methods for doing Formal Equivalence Verification (FEV) between RTL and Schematics are not efficient • Require one-to-one correspondence between the sequential elements in the compared models – Negative impact on the abstraction level of the RTL – Negative impact on design convergence as changes in the schematics need to be reflected in the RTL 4

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 5

Introduction • Formal Equivalence Verification (FEV) is the process of verifying that the schematic is functionally equivalent to the RTL • Formal verification tools are limited in capacity and complexity • Mapping is an association between signals in the compared designs – Central role in the FEV design activity – Thus defines boundaries for decompositions 6

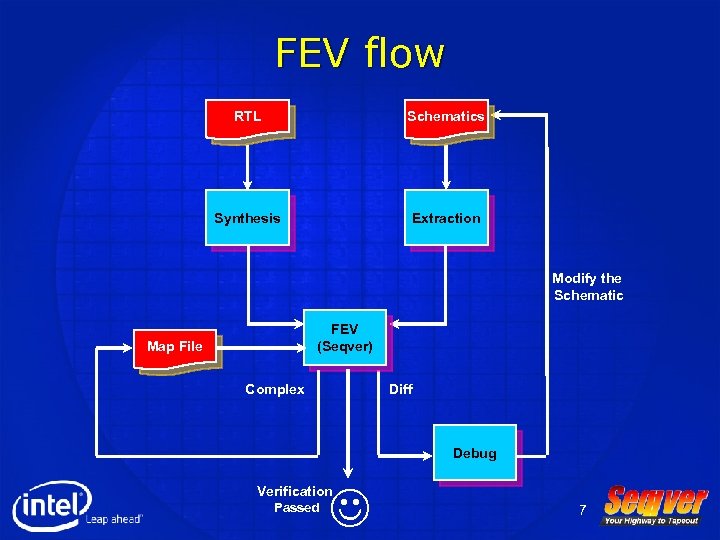
FEV flow RTL Schematics Synthesis Extraction Modify the Schematic FEV (Seqver) Map File Complex Diff Debug J Verification Passed 7

Traditional way of doing FEV • The designs are decomposed at the sequential elements – There is a one-to-one correspondence between the sequential elements in both designs • This method is called Combinational Equivalence Verification (CEV) RTL – Fub level Schematic – Fub level 8

Impact on chip design development • Detailed RTL is – – – Expensive to develop & maintain Slow to validate Error prone • Much of the design cycle deals with “tweaking” the circuit to meet timing/area/… constraints – Most of these changes should not change the visible behavior of a unit/fub. • Powerful, automatic, sequential verification can allow this tight coupling SCH-RTL to be relaxed 9

Sequential Equivalence Verification (SEV) • Compare designs in which there are different number of latches and/or locations of the latches RTL – Fub level Schematic – Fub level 10

SEV – Example 1 (Abstraction) Flip. Flop based memory implementation Latch RTL A[0] A[1] A[2] Out Dec A[n] D[0. . m] Schematic A[0] A[1] A[2] Latch based memory implementation Latch Pre Dec Post Dec Out A[n] D[0. . m] 11

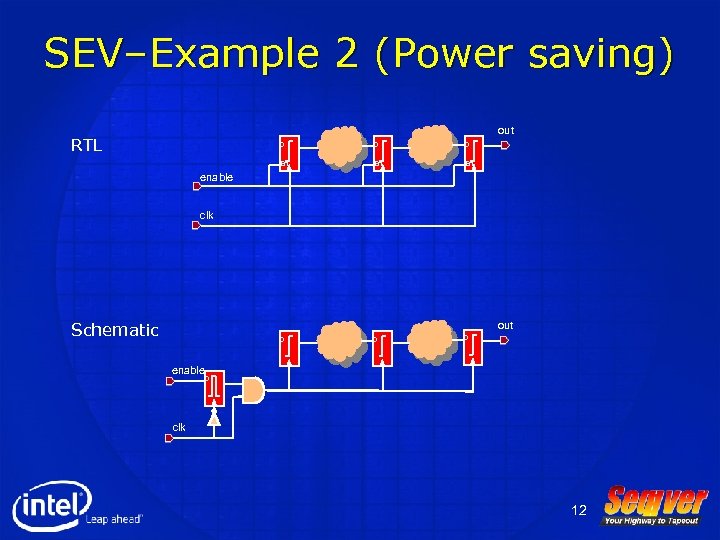
SEV–Example 2 (Power saving) out RTL D D D En En En D D D enable clk Schematic out enable D clk 12

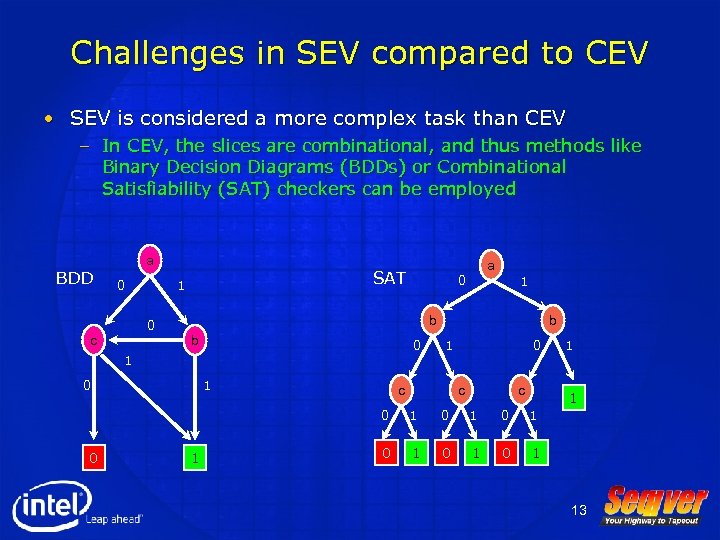
Challenges in SEV compared to CEV • SEV is considered a more complex task than CEV – In CEV, the slices are combinational, and thus methods like Binary Decision Diagrams (BDDs) or Combinational Satisfiability (SAT) checkers can be employed BDD a 0 0 c SAT 1 a 0 1 b b 0 1 b 1 c 0 c c 1 0 0 1 1 1 0 1 0 1 0 1 13

Challenges in SEV compared to CEV – Cont. • The most challenging question in SEV is initialization – What is the initial state of the two compared designs? – Example (retiming) RTL Schematic D out D 14

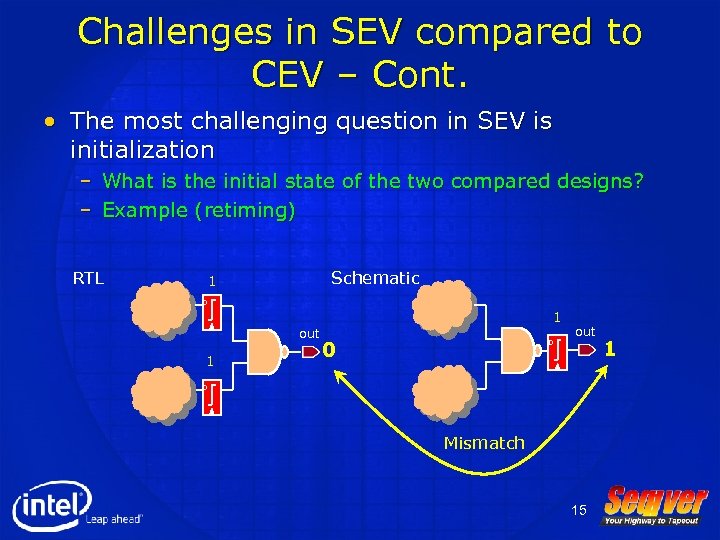
Challenges in SEV compared to CEV – Cont. • The most challenging question in SEV is initialization – What is the initial state of the two compared designs? – Example (retiming) RTL Schematic 1 D out 1 1 0 D out D Mismatch 15 1

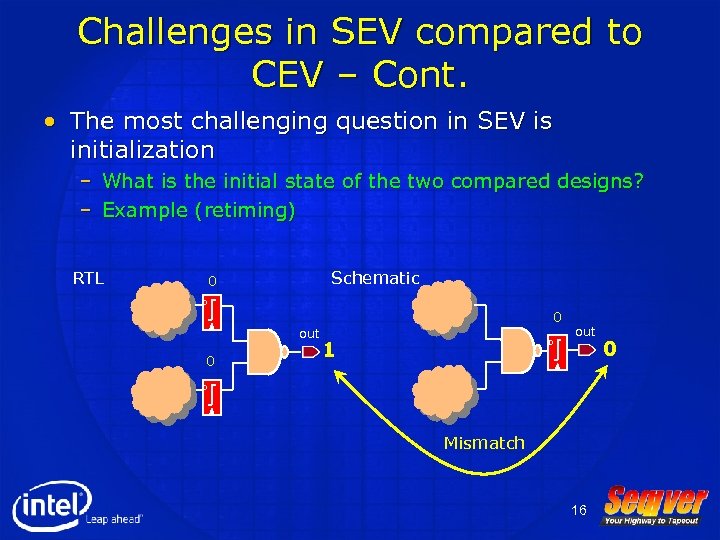
Challenges in SEV compared to CEV – Cont. • The most challenging question in SEV is initialization – What is the initial state of the two compared designs? – Example (retiming) RTL Schematic 0 D out 0 0 1 D out D Mismatch 16 0

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 17

What is ‘Seqver’? • Sequential EQuivalence VERifier • It addresses the following design activities: – Formal equivalence verification of two designs with similar or different placement of state elements – State matching (combinational) and non state matching designs verification – RTL 2 Sch, Sch 2 Sch and RTL 2 RTL • For more information, please refer to ICCD 2006 paper 18

How is the initialization problem addressed in Seqver? • Automatic initialization of the designs • Seqver theory is based on the alignability theory which was first introduced by Carl Pixley (1982) • It is motivated by the fact that a power-up state of a hardware design cannot be predicted or controlled • Thus the design must be brought into a smaller set of states where the design is supposed to work correctly 19

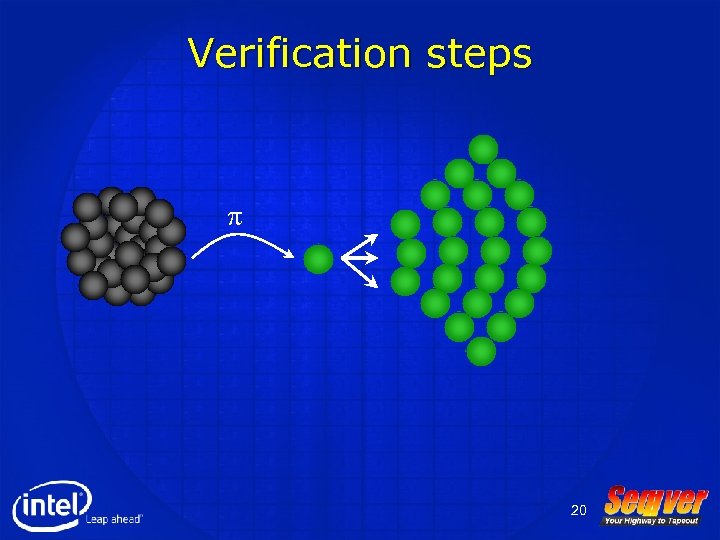
Verification steps p 20

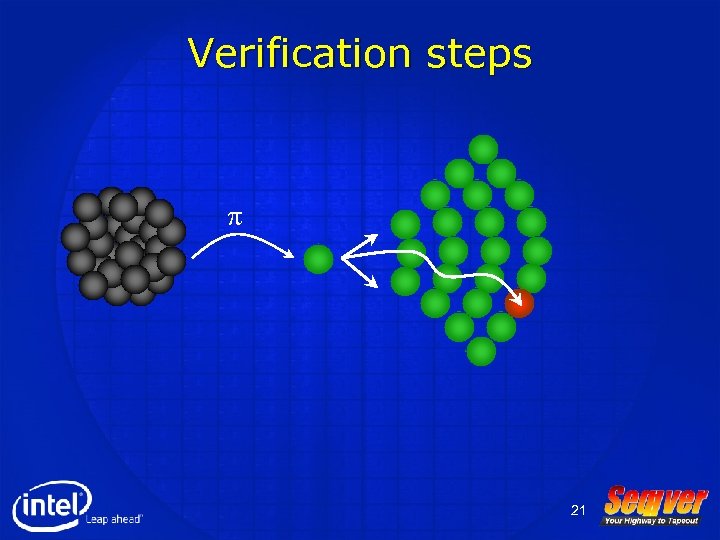
Verification steps p 21

Preliminaries • The unknown state of a circuit C is the state in which all the storage elements have the undefined value X • A binary state of a circuit C is a state in which all the state elements have binary values • An initialization sequence of C is a sequence of binary inputs which, when applied to the unknown state of C, brings C to a binary state • A reset sequence of C is a sequence of binary inputs which, when applied to any state of C, brings C to the same binary state • Without loss of generality, we will assume one circuit only that needs to be initialized – As the initialization sequence of the product machine of two given circuits C 2 and C 2 is an initialization sequence for each of them 22

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 23

Initialization algorithm • The idea is to assign the unknown value (X) on each of the sequential elements • Call formal engine to find an input sequence to the inputs that makes all the sequential element initialized with 0’s or 1’s • The theory guarantees no verification hole although the “real reboot sequence” might be different from the one found by Seqver • Example : possible initialization sequences are (A=0, B=0) (A=1, B=0) (A=0, B=1) (A=1, B=1) X RTL A Schematic D out B A X X D B 24 out X

Which formal engine to choose? • Traditional methods for initializing hardware designs are based on BDDs – Advantages: very convenient data structures – Disadvantages : very limited in terms of number of variables • We chose to use Satisfiability (SAT) based methods – Very powerful combinational and sequential engines – i. Prover : Intel Formal Technology SAT engines based on Eureka – world class SAT solver 25

Modeling challenges • Challenge: All the known SAT solvers are binary value based, while we need a three valued representation (modeling 0, 1, and X) • Solution: Dual rail modeling Dual Rail Encoding – Every signal is modeling using dual value (High, Low) Value Encoding – SAT is being applied in parallel 0 (0, 1) on both the high and low rails 1 (1, 0) – Due to the large similarity X (1, 1) between the high and low rails, Input a (a, !a) no overhead was observed due State s (s_H, s_L) to this duplication NOT (a, b) (b, a) (a, b) AND (c, d) (a AND c, b OR d) (a, b) OR (c, d) (a OR c, b AND d) 26

Modeling challenges – Cont. • Challenge: How do we model sequential behavior using propositional logic? • Solution: Every variable is represented using infinite sequence • Unrolling operation of an output function up-to depth k simply means applying the Next operator k times • We denote the value of stream v at time k using v[k] Sequential Logic Encoding Value Modeling 0 0, 0, 0, … 1 1, 1, 1, … Input a a 0, a 1, a 2, … NOT a !a 0, !a 1, !a 2, … a AND b a 0 AND b 0, a 1 AND b 1, a 2 AND b 2 , … a OR b a 0 OR b 0, a 1 OR b 1, a 2 OR b 2 , … Next a a 1, a 2, … 27

So what’s novel in our method ? • Recall that our method assumed all the sequential elements are initialized with the unknown value (X) • The main drawback of this methods is that sometimes the circuit is resettable but the described method wouldn’t find the reset sequence – Due to weakness properties of X (X AND !X = X) – The described method could find a sequence that initializes partial set of the sequential elements – A novel method was developed in order to complement this sequence 28

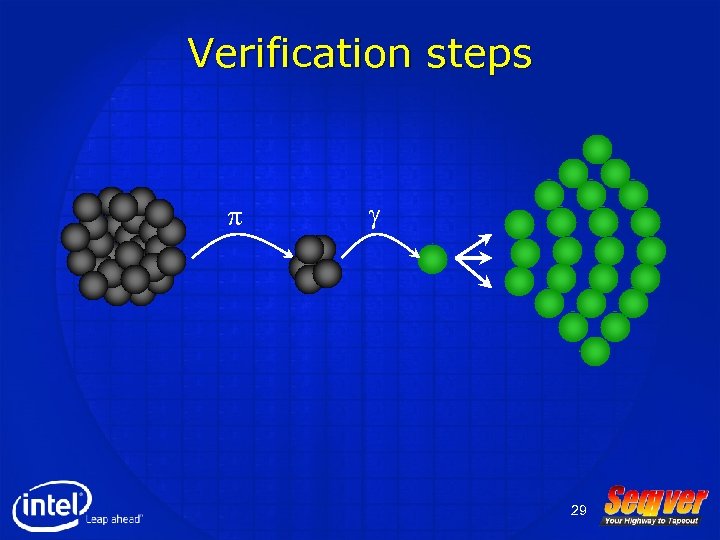
Verification steps p g 29

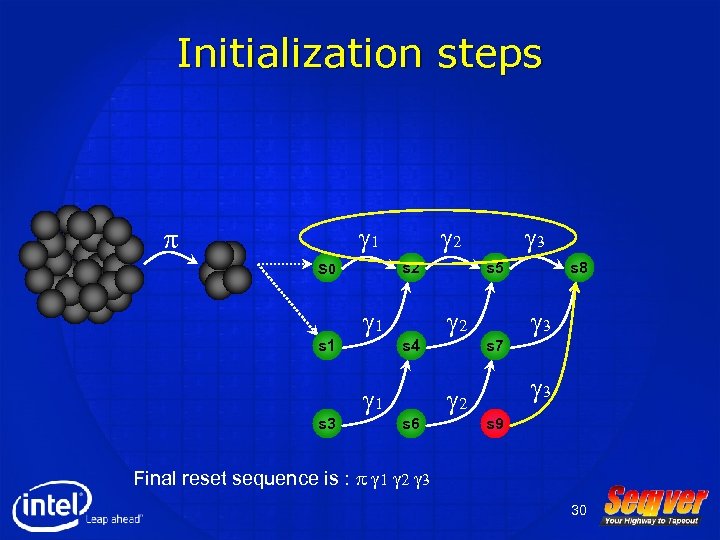
Initialization steps g 1 p s 0 s 1 s 3 g 2 s 2 g 1 s 4 s 6 g 3 s 5 g 2 s 7 s 8 g 3 s 9 Final reset sequence is : p g 1 g 2 g 3 30

Algorithm illustration 31

Algorithm illustration p Stage 1 : Initialize all the state elements with X. Find initialization sequence p 32

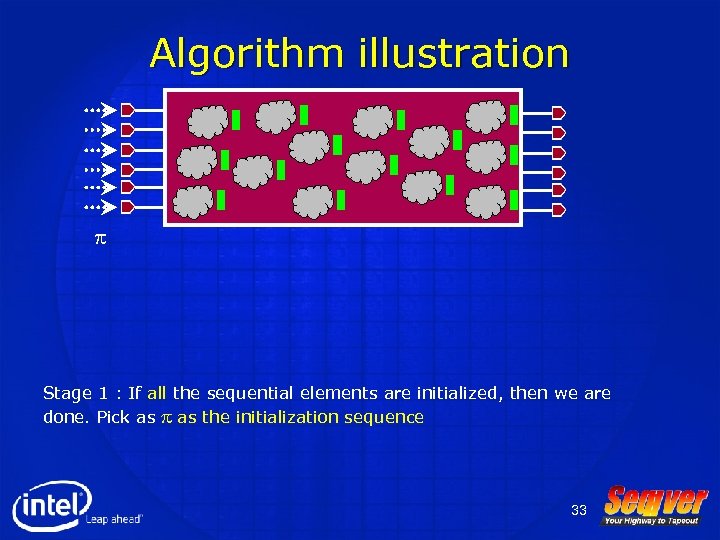
Algorithm illustration p Stage 1 : If all the sequential elements are initialized, then we are done. Pick as p as the initialization sequence 33

Algorithm illustration p Stage 2 : If not all the sequential elements are initialized, then 34

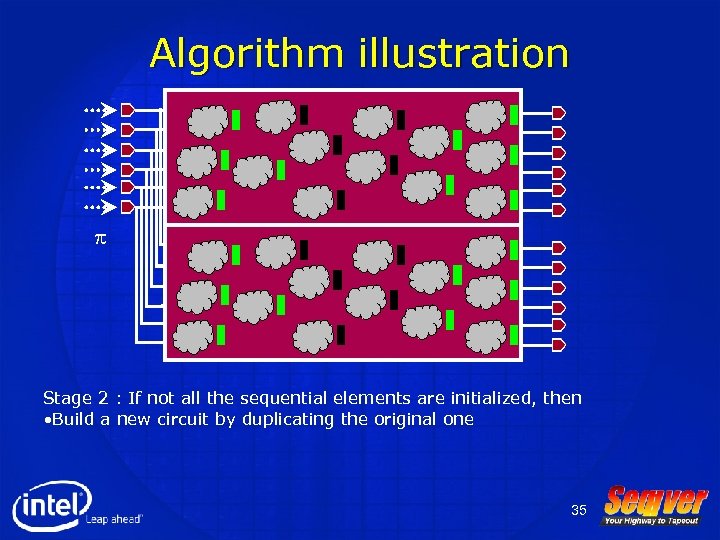
Algorithm illustration p Stage 2 : If not all the sequential elements are initialized, then • Build a new circuit by duplicating the original one 35

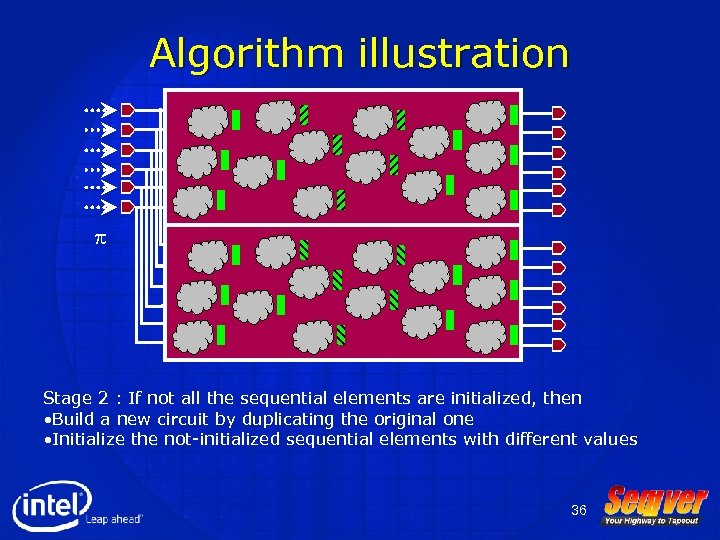
Algorithm illustration p Stage 2 : If not all the sequential elements are initialized, then • Build a new circuit by duplicating the original one • Initialize the not-initialized sequential elements with different values 36

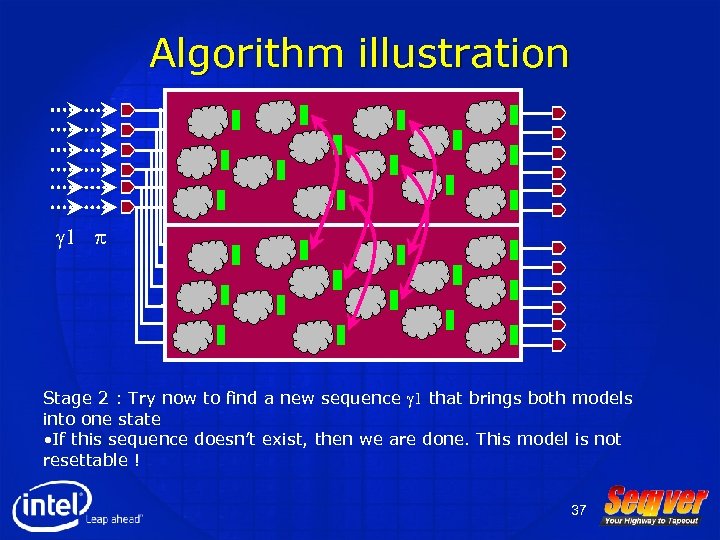
Algorithm illustration g 1 p Stage 2 : Try now to find a new sequence g 1 that brings both models into one state • If this sequence doesn’t exist, then we are done. This model is not resettable ! 37

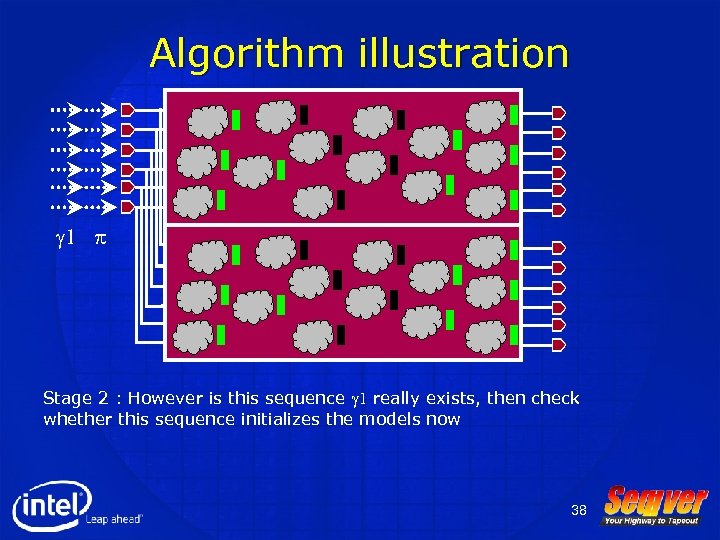
Algorithm illustration g 1 p Stage 2 : However is this sequence g 1 really exists, then check whether this sequence initializes the models now 38

Algorithm illustration g 1 p 39

Algorithm illustration g 1 p 40

Algorithm illustration g 2 g 1 p 41

Algorithm illustration g 2 g 1 p 42

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 43

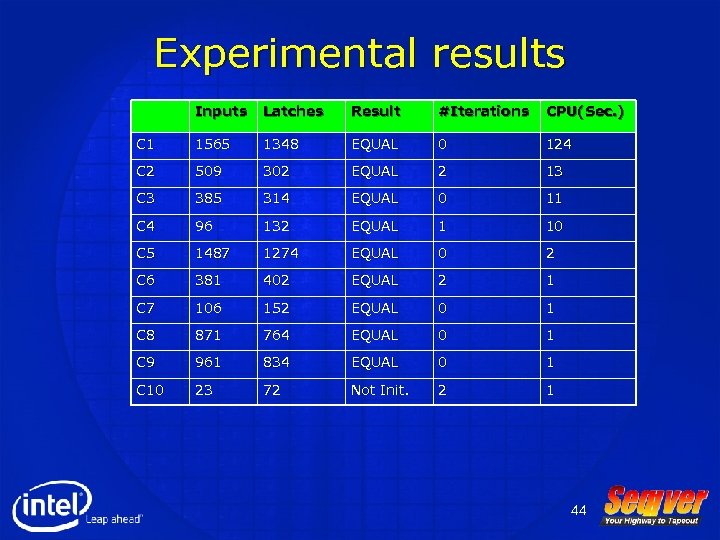
Experimental results Inputs Latches Result #Iterations CPU(Sec. ) C 1 1565 1348 EQUAL 0 124 C 2 509 302 EQUAL 2 13 C 3 385 314 EQUAL 0 11 C 4 96 132 EQUAL 1 10 C 5 1487 1274 EQUAL 0 2 C 6 381 402 EQUAL 2 1 C 7 106 152 EQUAL 0 1 C 8 871 764 EQUAL 0 1 C 9 961 834 EQUAL 0 1 C 10 23 72 Not Init. 2 1 44

Agenda • • • Problem statement Introduction What is Seqver? Initialization algorithm Experimental results Conclusions 45

Conclusions • Sequential equivalence verification using ‘Seqver’ opens the door for raising the RTL abstraction • First large scale usage in Intel – hundreds of designers • A new approach which automates the generation of initial state for hardware designs • New sequential modeling techniques empowered with world-class combinational SAT solvers enables solving tough sequential problems like ATPG and automatic sequential property verification 46

Questions