Индексы Понятие индекса Индекс относительная величина

Индексы

Понятие индекса Индекс – относительная величина сравнения во времени и в пространстве одноименных явлений и сложных совокупностей. Изменение одноименных явлений изучается при помощи индивидуальных индексов (i), которые представляют собой относительные величины сравнения, динамики, выполнения плана, например, индивидуальный индекс физического объема производства iq = где q 1, q 0 – физические объемы производства изделия в отчетном и базисном периодах,

Понятие сложной совокупности Изменение сложных совокупностей изучают при помощи групповых или общих индексов (I). Сложной называется совокупность элемента которой не подлежат суммированию. Для того, чтобы осуществить расчет общих индексов необходимого выбрать соизмеритель. Например, для расчета изменений физического объема производства соизмерителем могут быть выбрана цена (p), себестоимость (z), трудоемкость (t). Формы общих индексов: n агрегатная n средневзвешенные из индивидуальных

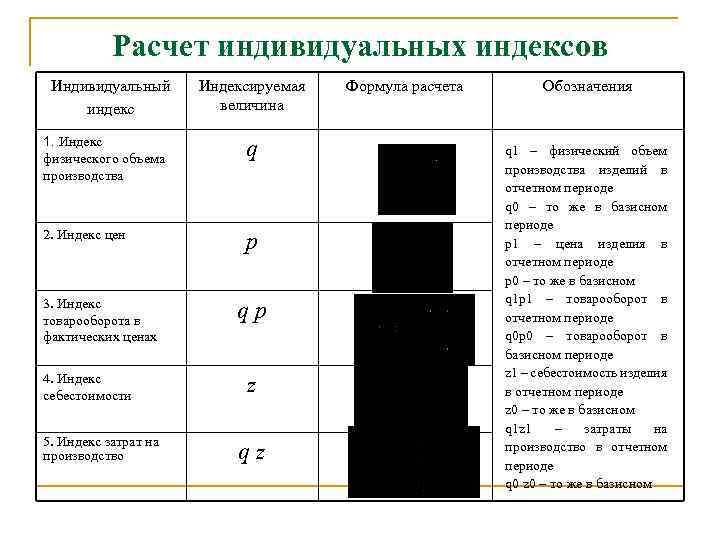Расчет индивидуальных индексов Индивидуальный индекс Индексируемая величина 1. Индекс физического объема производства q 2. Индекс цен p 3. Индекс товарооборота в фактических ценах 4. Индекс себестоимости 5. Индекс затрат на производство qp z qz Формула расчета Обозначения q 1 – физический объем производства изделий в отчетном периоде q 0 – то же в базисном периоде p 1 – цена изделия в отчетном периоде p 0 – то же в базисном q 1 р1 – товарооборот в отчетном периоде q 0 р0 – товарооборот в базисном периоде z 1 – себестоимость изделия в отчетном периоде z 0 – то же в базисном q 1 z 1 – затраты на производство в отчетном периоде q 0 z 0 – то же в базисном

Общие индексы в агрегатной форме Агрегатные индексы являются основной формой общих индексов. В числителе и знаменателе общего индекса в агрегатной форме содержатся соединенные наборы элементов совокупности (агрегаты) – суммы произведений. Условие использования : Используются агрегатные индексы в том случае, если исходная информация содержит данные об объемах производства (продаж) в натуральных измерителях и цене (себестоимости) за единицу продукции. Если рассчитывается индекс количественного показателя, то соизмерителем выступает цена (себестоимость, трудоемкость) изделий. Соизмеритель принимается на уровне базисного периода в агрегатной форме индекса Э. Ласпейреса. Соизмеритель принимается на уровне отчетного периода в агрегатной форме индекса Г. Пааше. Если рассчитывается индекс качественного показателя, то соизмерителем является количество произведенной (реализованной) продукции, которое принимается на уровне отчетного периода (индекс Г. Пааше) или на уровне базисного периода (индекс Э. Ласпейреса.

Расчет общих индексов в агрегатной форме 1. Индекс физического объема по формуле Ласпейреса. Соизмеритель ( p)в индексе Ласпейреса принимается на уровне базисного периода. 2. Индекс цен по формуле Пааше. Соизмеритель ( q) в индексе Пааше принимается на уровне отчетного периода.

Взаимосвязь общих индексов в агрегатной форме Связь общих индексам. индексов аналогична индивидуальным Iqp - Верхний индекс "л" указывает индекс Ласпейреса, а "п" – Пааше. Iqp = - индекс товарооборота в фактических ценах Iq = - индекс физического объема Ip = - индекса цен, тогда

Абсолютные отклонения Δqp = Δqp(q) + Δqp(p) Изменение товарооборота в фактических ценах n Δqp = Σq 1 p 1 – Σq 0 p 0, в том числе за счет факторов: а) изменение товарооборота за счет физического объема производства Δqp(q) = Σq 1 p 0 – Σq 0 p 0 б) изменение товарооборота за счет цен Δqp(p) = Σp 1 q 1 – Σp 0 q 1

Индексы Фишера и Лоу Средним геометрическим индексом из индексов Пааше и Ласпейреса является индекс И. Фишера. Индекс Фишера используется для исчисления индекса цен за длительный период времени. n Если для расчетов качественных показателей используется средний физический объем производства ( ), то общий индекс называется индексом Лоу, он используется для расчетов за длительное время. n

Общие индексы в средней форме n Средние индексы используются в том случае, когда исходная информация не содержит данных об объемах производства (продаж) в натуральных измерителях, но имеются данные об объемах реализации в стоимостных измерителях и ценах за единицу продукции. n Средние индексы получают путем преобразования агрегатных индексов. Если преобразования производят в числителе агрегатного индекса, то получаем средний арифметический взвешенный индекс, а если преобразуют знаменатель агрегатного индекса, то получают средний гармонический взвешенный индекс

Преобразование индекса физического объема производства Индекс физического объема производства Вспомним формулу индивидуального индекса физического объема производства Выразим из формулы индивидуального индекса Получим производное выражение , которое подставим в числитель формулы агрегатного индекса физического объема производства

Преобразование индекса цен Формула агрегатного индекса цен Вспомним формулу индивидуального индекса цен Выразим из формулы индивидуального индекса Получим производное выражение , которое подставим в числитель формулы агрегатного индекса физического объема производства

Взаимосвязь общих индексов в средней форме Связь общих индексов аналогична агрегатным индексам.

Индексы переменного, постоянного состава и структурных сдвигов Индекса переменного, постоянного состава и структурных сдвигов являются общими индексами. Они характеризуют изменение среднего значения индексируемого показателя. Данные индексы используются для анализа совокупности однородных единиц (одноименная продукция, материалы и т. д. ) Цель расчета – выявить влияние отдельных факторов на изменение среднего значения индексируемой величины. При расчете выявляют внимание факторов: nизменение индексируемого показателя nизменение структуры совокупности

Индекс переменного состава n. Индекс переменного состава показывает изменение самой средней величины. или по формуле средней арифметической взвешенной Если удельные веса (доли) то получим обозначить d 1 и d 0 ,

Индекс постоянного состава На изменение средней цены влияют два фактора: nизменение цены определяется индексом постоянного состава Структура производства и в числителе и в знаменателе дроби берется отчетной.

Индекс структурных сдвигов Влияние структуры на изменение средней цены показывает индекс структуры сдвигов Цена в числителе и знаменателе формулы принимается базисная.

Взаимосвязь между индексами переменного, постоянного состава и структурных сдвигов Между индексами переменного, постоянного и структурных сдвигов существует связь. состава

Абсолютное изменений средней цены Абсолютные изменения средней цены , в том числе за счет влияния факторов: n за счет изменения средней цены: n за счет изменения структуры

Цепные и базисные индексы Цепные индексы получают путем сопоставления показателя любого периода с показателем предшествующего периода. Базисные индексы получают сравнением показателя любого периода с показателем периода, принятого за базу сравнения.

Правила перехода Произведение цепных индивидуальных индексов равно базисному индексу последнего из взятых периодов 2. Базисный агрегатный индекс физического объема продукции может быть получен как произведение цепных агрегатных индексов при постоянных соизмерителях (весах). Агрегатные индексы качественных показателей, рассчитанные по формуле Паше, всегда являются индексами с меняющимися весами, поэтому цепной метод исчисления базисных индексов не применяется. Если же воспользоваться формулой Ласпейреса для расчета агрегатных индексов цен при условии постоянных весов q для всех периодов, то базисные индексы могут быть определены на основе цепных. 1.

Цепные индексы физического объема производства Индивидуальные индексы: Агрегатные индексы: , ,

Цепные индексы цен Индивидуальные индексы: Агрегатные индексы: , ,

Базисные индексы физического объема производства n Индивидуальные индексы: n Агрегатные индексы: , ,

Базисные индексы цен n Индивидуальные индексы: n Агрегатные индексы: , ,