Индексы Индекс —

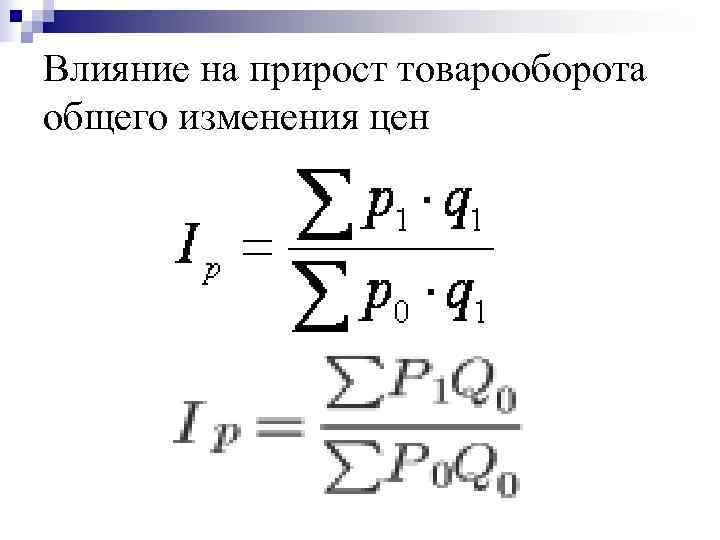
Индексы

Индекс - n относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях; n используются: для сопоставления уровней явлений; для установления значимости причин, вызывающих их изменение

Экономический индекс n относительная величина, характеризующая изменение изучаемого явления во времени, пространстве или по сравнению с некоторым эталоном

Экономический индекс По степени охвата явлений По виду По базе весов сравнения Индексы По форме По составу явления По содержанию индексируемых величин

Экономический индекс По степени охвата элементов совокупности Индивидуальные Общие Групповые Тотальные

Экономический индекс n Индивидуальный - соотношение простых единичных показателей (i) n Общий – обобщенная характеристика изменения показателя n Групповой - общий, характеризующий изменение определенного показателя по группе (I) n Тотальный – общий, характеризующий изменение определенного показателя в целом по какой-либо сложной совокупности

Экономический индекс По виду весов С переменными весами С постоянными весами Базисного Отчетного периода

Экономический индекс n С переменными весами – последовательность индексов, веса которых меняются от одного индекса к другому n С постоянными весами – при вычислении которых используют неизменные значения весов

Экономический индекс По форме Агрегатные Средние взвешенные Арифметические Гармонические

Экономический индекс n Агрегатный – числитель и знаменатель представляют суммы произведений двух величин, одна из которых индексируется (изменяется), а другая остается фиксированной в числителе и знаменателе (выступает в качестве веса ) n Средние взвешенные – производные из агрегатных

Экономический индекс По базе сравнения Индексы выполнения Динамические Территориальные плана Цепные Базисные

Экономический индекс n Выполнения плана – если отчетный период сопоставляется с плановым n Динамические – изменение изучаемого явления во времени n Территориальные – изменение развития различных территорий

Экономический индекс По составу явления Постоянного Переменного (фиксированного) состава Средних уровней

Экономический индекс n Постоянного состава – агрегатный индекс вес которого фиксируется на определенном периоде n Переменного состава – отношение двух средних уровней изучаемого явления, относящиеся к разным периодам

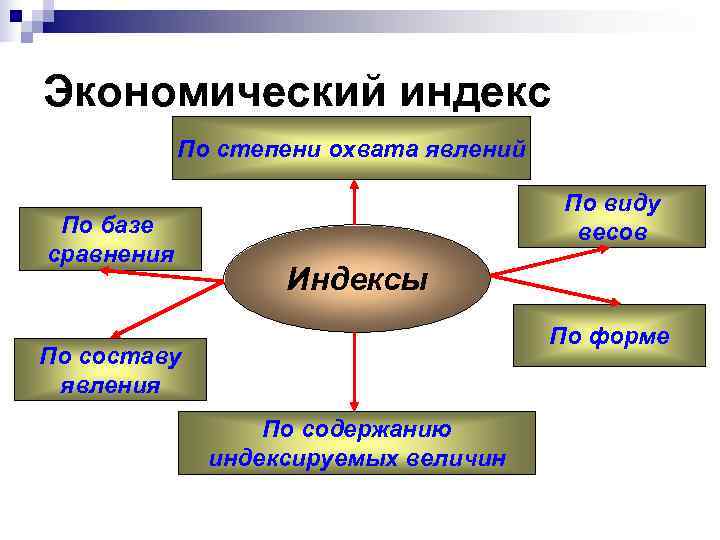
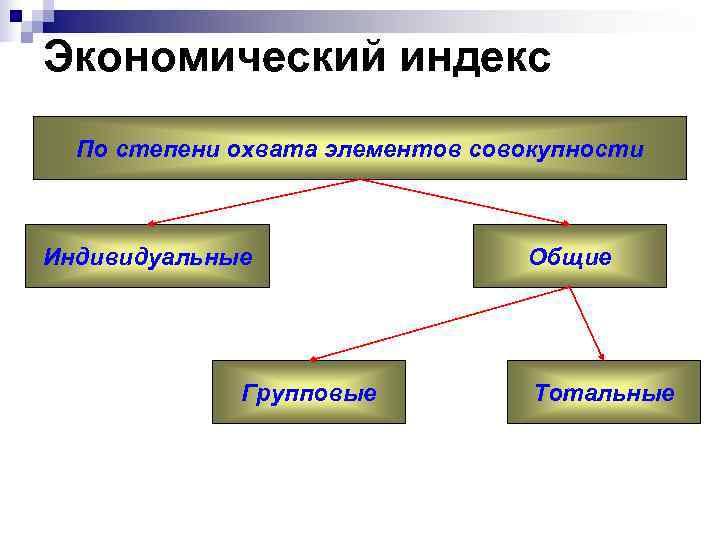
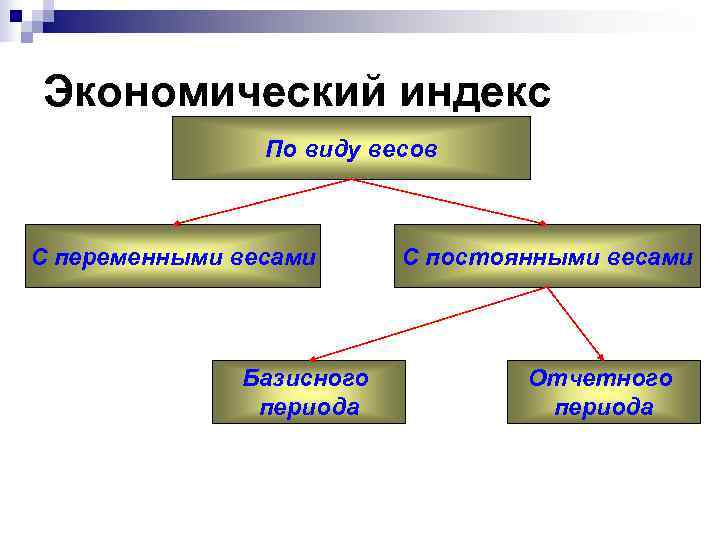
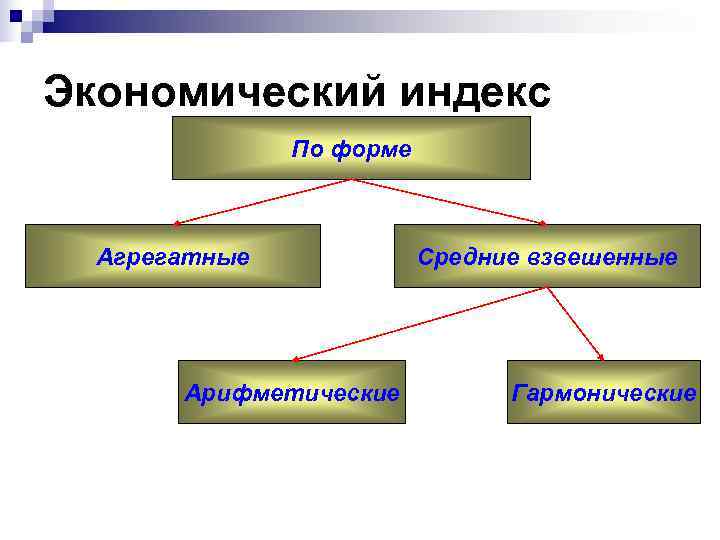
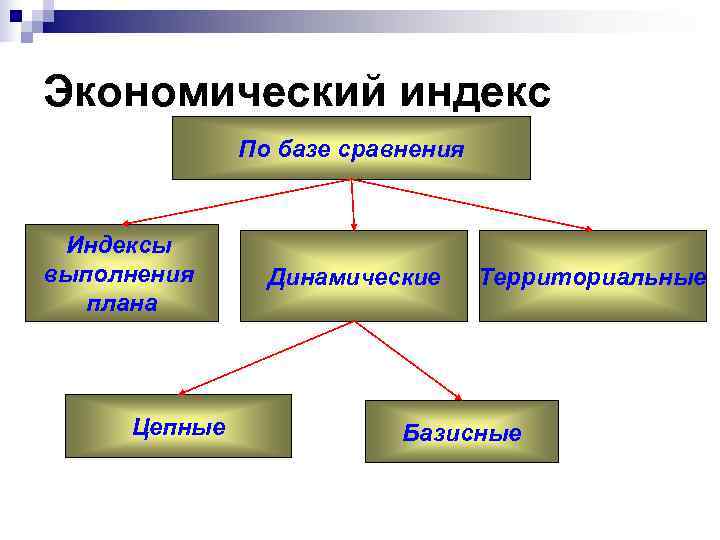
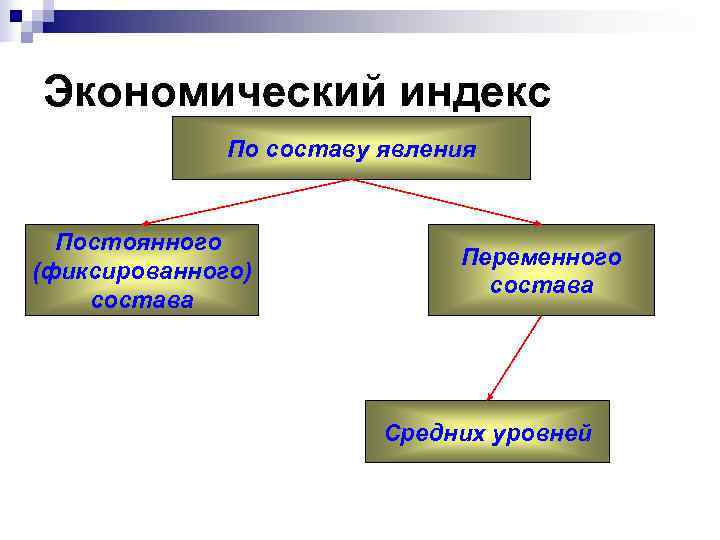
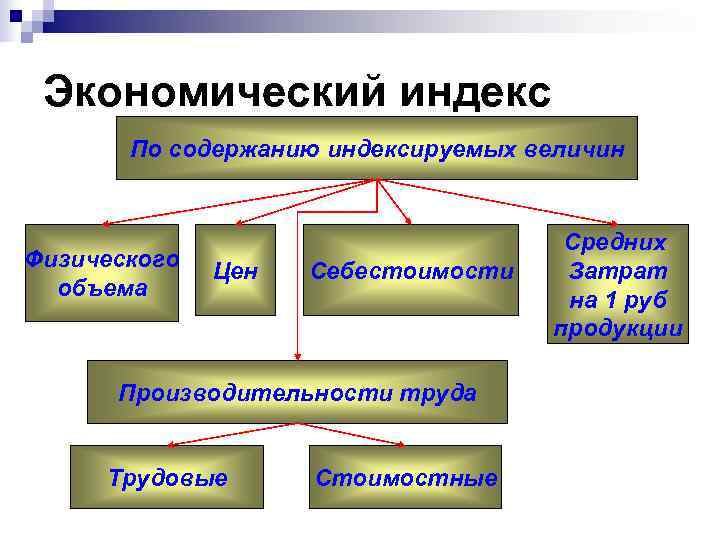
Экономический индекс По содержанию индексируемых величин Средних Физического Цен Себестоимости Затрат объема на 1 руб продукции Производительности труда Трудовые Стоимостные

По виду индексируемых величин: n. Объёмные индексы служат для измерения изменения объёмных показателей, выраженных абсолютными величинами. Получаются как итог непосредственного подсчета или суммирования; являются исходными, первичными (физ. объём выпуска продукции (шт. ), численность работающих общие затраты труда на производство продукции, общая себестоимость продукции и т. п).

По виду индексируемых величин: n Качественные (взвешевающие) индексы служат для измерения изменения качественных показателей, определяемых в расчете на количественную единицу (цена, себестоимость или трудоёмкость единицы продукции, производительность труда); Получаются путем деления объемных показателей , носят расчетный, вторичный характер; как правило, являются либо средними, либо относительными величинами.

В индексном анализе принято правило: n индексы качественных показателей (цен, себестоимости и т. п. ) строятся с весами отчетного периода , индексы количественных показателей (количества выпущенной продукции, физического объема товарооборота) - с весами базисного периода.

Различают два основных вида индексов: n простые (частные, индивидуальные); n аналитические (общие, агрегатные).

Простые индивидуальные индексы n Применяются если анализируются простые явления или не имеет значения структура сложных явлений n исследуемый признак принимается без учета связи этого признака с остальными признаками исследуемых экономических явлений

Индивидуальный индекс характеризует изменение отдельного элемента совокупности. n индивидуальный индекс количества проданных товаров n индивидуальный индекс цены n индивидуальный индекс себестоимости ( затрат) n индивидуальный индекс трудоемкости n индивидуальный индекс товарооборота (выручки от продаж)

Индивидуальный индекс сложного явления формируется из индексов простых его составляющих по типологической формуле его определения: двухфакторная мультипликативная модель сложного явления, позволяющая находить его изменение под влиянием каждого фактора в отдельности. i q показывает, во сколько раз увеличилась (или уменьшилась) общая сумма выручки под влиянием изменения объема продажи в натуральных единицах. i p показывает, во сколько раз изменилась общая сумма выручки под влиянием изменения цены товара.

Анализ по факторам n Общее изменение выручки (прирост) равняется ∆ Q =Q 1 -Q 0, а ее изменение от каждого фактора определяется следующим образом: n От изменения количества товара при постоянной цене (ip = 1) оно равно ∆ Q q= iq. Q 0 - Q 0 = (iq – 1) Q 0, n при изменении цены оно будет равным ∆ Q p= Q 1 - Q 0 - ∆ Qq = iqip. Q 0 - (iq – 1) Q 0= = iq(ip – 1) Q 0

трехфакторная индексная мультипликативная модель n. М = qmp, M 1=iqimip. M 0. n - трехфакторная индексная мультипликативная модель материальных затрат на выпуск продукции , где q - объем выпуска продукции, т - удельный расход материала р - его цена,

Индивидуальный индекс

Общие (аналитические, агрегатные)индексы n Индекс становится общим, когда в расчетной формуле показывается неоднородность изучаемой совокупности (общая масса проданных товаров нескольких видов). Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например: Q = Σpq nизучаемый признак используется не изолированно, а в его взаимосвязи с другими признаками. n. Поэтому любой аналитический индекс состоит из двух элементов: nиндексируемый признак , то есть тот признак, изменение которого подвергается изучению;

Общий агрегатный индекс - относительный показатель, характеризующий среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов; - общие индексы простых явлений не отражают взаимосвязи между собой в сложном явлении и потому считаются необъективными агрегат - сумма произведений взвешивающего показателя на объемный

индекс общего объёма товарооборота в агрегатной форме:

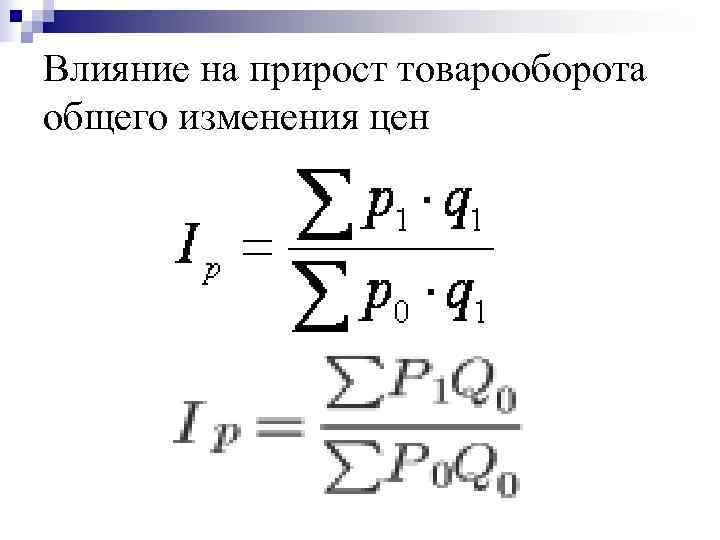Влияние на прирост товарооборота общего изменения цен

Влияние на прирост товарооборота изменения количества проданных товаров

Общий агрегатный индекс n Простой n Средний n Взвешенный

Агрегатные индексы n Индексируемый признак – это признак, изменение которого характеризует данный индекс (например, в Iq – это q). n Признак – вес выполняет функцию веса по отношению к индексируемому признаку (так в Ip признаком веса является q).

Агрегатные индексы n Если индексируемый признак меняется в отчетном периоде по сравнению с базисным, а признак –вес берется на базисном уровне, то агрегатная форма индекса рассчитывается по формуле Ласпейреса

Агрегатные индексы n Если при тех же условиях признак-вес берется на уровне отчетного периода, то такие агрегатные индексы исчисляются по формуле Пааше

Общий агрегатный индекс Вид Наименование Формула Простой количества Простой цен Простой средний количества Взвешенный Цен Количеств (Ласпейреса) (Лайсперса) Количеств (Пааше) Фишера

Правило агрегатных индексов Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки.

Идеальный индекс Фишера — это средняя геометрическая из произведения двух агрегатных индексов Пааше и Ласпейреса: Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса).

Сравнение индивидуального и агрегатного индексов

Наиболее употребительные агрегатные индексы: n Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства (q) и затрат на единицу (z): n Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих (Т) и заработной платы (f):

n Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w): n Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования - фондоотдачи (Н):

Правила: n Обратимость во времени – если индекс показывает снижение показателя в отчетном периоде в n раз, то в базисном, он должен показать увеличение в n раз; n Обратимость по факторам – если поменять местами в индексе цен символы цен и количества, то должны получить индекс количества.

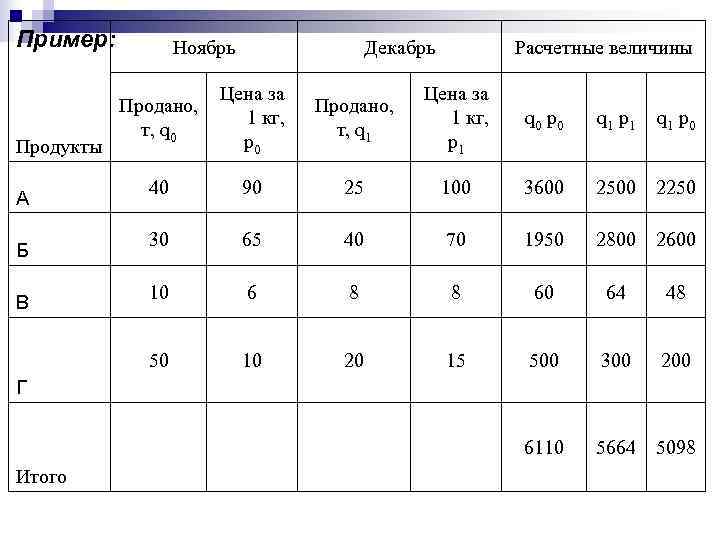
Пример: Ноябрь Декабрь Расчетные величины Цена за Продано, 1 кг, q 0 p 0 q 1 p 1 q 1 p 0 т, q 1 Продукты p 0 p 1 40 90 25 100 3600 2500 2250 А 30 65 40 70 1950 2800 2600 Б 10 6 8 60 64 48 В 50 10 20 15 500 300 200 Г 6110 5664 5098 Итого

общий (сводный) индекс объема реализации (товарооборота) Общий индекс объема реализации продукции снизился на 7. 3% Разница между числителем и знаменателем дает абсолютную величину изменений

общий индекс цен Общий индекс цен -уровень цен вырос на 11% Разница между числителем и знаменателем дает абсолютную величину изменений

общий индекс физического объема Общий индекс физ. объема реализованной продукции снизился на 16, 6% Разница между числителем и знаменателем дает абсолютную величину изменений

Между рассчитанными индексами существует связь Общий объем реализации (товарооборот) уменьшился на 7, 3% ; Абсолютная величина изменений:

Средние индексы - индексы, вычисленные как средняя взвешенная величина из индивидуальных индексов n Арифметическая форма индекса используется для сводных индексов количественных показателей, n Гармоническая форма индекса – для расчета сводных индексов качественных показателей

Преобразование агрегатного индекса в средний из индивидуальных : n либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. n Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический , если же в знаменателе, то - в средний гармонический из индивидуальных индексов.

Преобразование агрегатного индекса в средний из индивидуальных : 1. Средний арифметический – среднее арифметическое из индивидуальных индексов, взвешенных по стоимости продукции базисного периода Т. е. в числителе сводного индекса физ. кол-ва можно использовать замену: iq= q 1 / q 0 q 1= iq* q 0

Преобразование агрегатного индекса в средний из индивидуальных : 2. Средний гармонический – среднее гармоническое из величин, обратных индивидуальным индексам цен, взвешенных по стоимости продукции отчетного периода. Т. е. в знаменателе сводного индекса цен можно использовать замену: ip = p 1 / p 0 = p 1 / ip

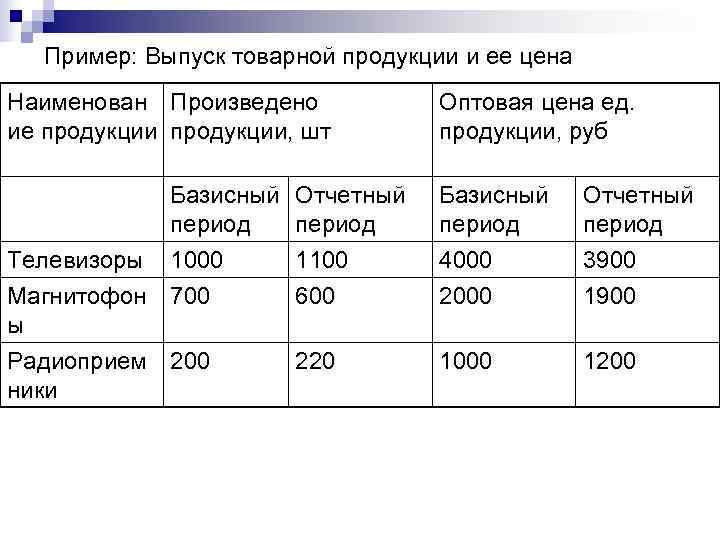
Пример: Выпуск товарной продукции и ее цена Наименован Произведено Оптовая цена ед. ие продукции, шт продукции, руб Базисный Отчетный период Телевизоры 1000 1100 4000 3900 Магнитофон 700 600 2000 1900 ы Радиоприем 200 220 1000 1200 ники

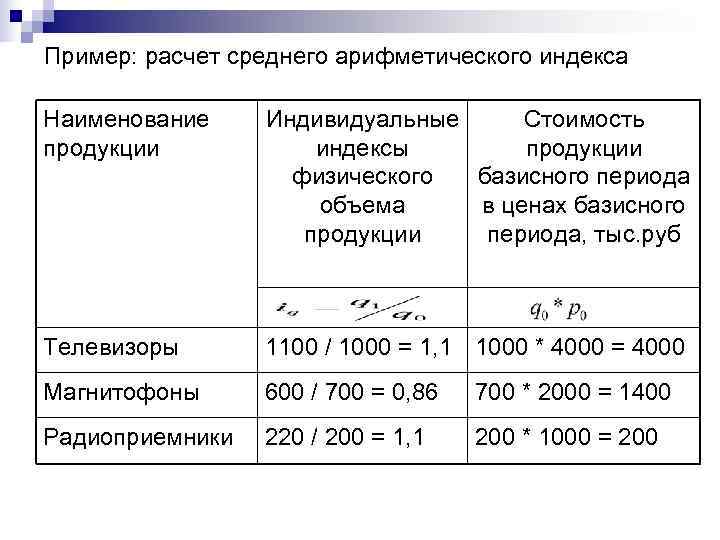
Пример: расчет среднего арифметического индекса Наименование Индивидуальные Стоимость продукции индексы продукции физического базисного периода объема в ценах базисного продукции периода, тыс. руб Телевизоры 1100 / 1000 = 1, 1 1000 * 4000 = 4000 Магнитофоны 600 / 700 = 0, 86 700 * 2000 = 1400 Радиоприемники 220 / 200 = 1, 1 200 * 1000 = 200

Средний арифметический индекс

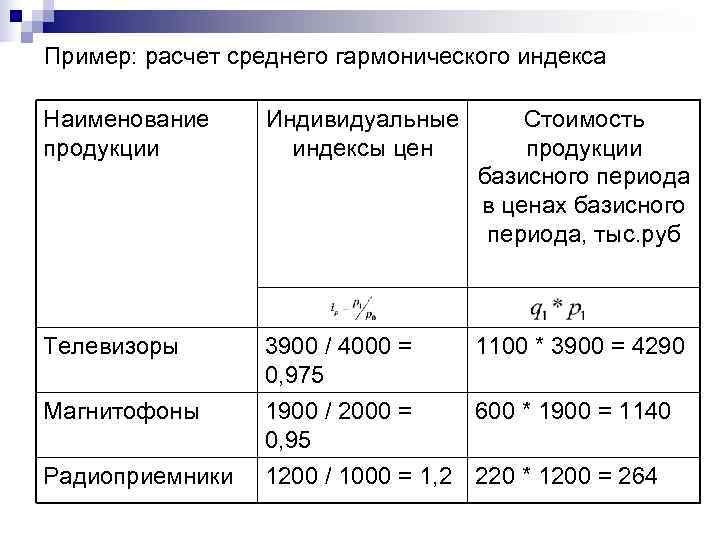
Пример: расчет среднего гармонического индекса Наименование Индивидуальные Стоимость продукции индексы цен продукции базисного периода в ценах базисного периода, тыс. руб Телевизоры 3900 / 4000 = 1100 * 3900 = 4290 0, 975 Магнитофоны 1900 / 2000 = 600 * 1900 = 1140 0, 95 Радиоприемники 1200 / 1000 = 1, 2 220 * 1200 = 264

Средний гармонический индекс

n Влияние на динамику среднего уровня изучаемого явления отдельных факторов, может быть изучено с помощью системы взаимосвязанных индексов: индекса постоянного состава, индекса переменного состава, индекса структурных сдвигов

Показатель динамики среднего показателя называется индексом переменного состава n Ипер. С = произведению двух индексов: индекса постоянного состава на индекс структурных сдвигов.

Средняя цена единицы товара определяется по формуле средней арифметической взвешенной: Следовательно, изменение средней цены можно выразить в виде индекса: -отношение двух средних с переменными весами; - зависит от следующих факторов: изменения самих цен (выражается индексом постоянного состава) и структурных сдвигов в товарообороте

Индекс осредняемого показателя в неизменной структуре называется индексом постоянного состава nвсегда сопоставляется с весами отчетного периода nхарактеризует динамику двух средних величин при одинаковой фиксированной структуре совокупности в отчетном периоде nвсе индексы качественных показателей (цены, себестоимости, производительности труда) являются индексами в неизменной структуре, или индексами постоянного состава

индекс постоянного (фиксированного) состава n изменение средней цены можно выразить в виде индекса: Ипост С. характеризует изменение средней величины только за счет влияния индексируемых величин при постоянных весах

Индекс структурных сдвигов – это отношение двух средних величин, рассчитанных для разной структуры совокупности; взвешивается по весам базисного периода. равен отношению индекса переменного состава к индексу постоянного состава

Так как может применяться не только количество реализованной продукции, но и удельный вес отдельных групп товаров, индекс структурных сдвигов может быть выражен в следующем виде: Экономическая сущность ИСС состоит в том, что он показывает, во сколько раз изменился общий средний уровень только за счет изменения удельного веса каждого объекта в общем объеме количественного признака

Взаимосвязь этих индексов в итоге можно выразить следующим образом:

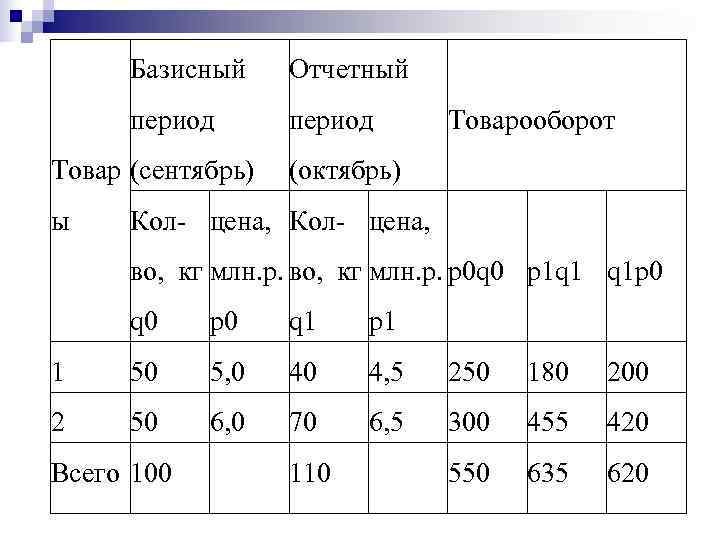
Базисный Отчетный период Товарооборот Товар (сентябрь) (октябрь) ы Кол- цена, во, кг млн. р. p 0 q 0 p 1 q 1 q 1 p 0 q 0 р0 q 1 р1 1 50 5, 0 4, 5 250 180 200 2 50 6, 0 70 6, 5 300 455 420 Всего 100 110 550 635 620

или 105, 5%. (переменного состава)

Таким образом, ср. цена за месяц увеличилась за счет: а) изменения цен на рынках или 102, 4%. (постоянного состава) б) за счет изменения соотношения продаж между рынками:

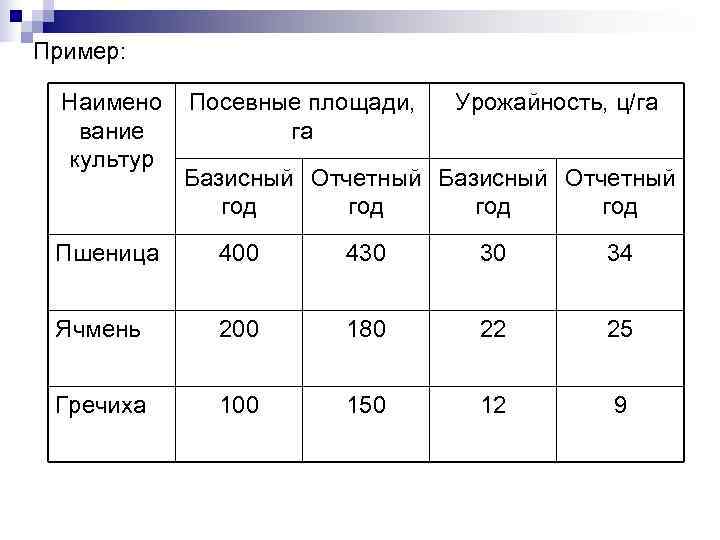
Пример: Наимено Посевные площади, Урожайность, ц/га вание га культур Базисный Отчетный год год Пшеница 400 430 34 Ячмень 200 180 22 25 Гречиха 100 150 12 9

Пример: Индекс средней урожайности

Пример: Индекс изменения средней урожайности за счет урожайности отдельных структур

Пример: Индекс изменения средней урожайности за счет изменения структуры посевных площадей