0bef1d780e63acfb079db8e9b59b4d62.ppt
- Количество слайдов: 26
 INCS 741: Cryptography Key Management and Diffie. Hellman Dr. Monther Aldwairi New York Institute of Technology. Amman Campus 12/3/2009 Dr. Monther Aldwairi 1
INCS 741: Cryptography Key Management and Diffie. Hellman Dr. Monther Aldwairi New York Institute of Technology. Amman Campus 12/3/2009 Dr. Monther Aldwairi 1
 Key Management • public-key encryption helps address key distribution problems • two aspects of this: – distribution of public keys – use of public-key encryption to distribute secret keys
Key Management • public-key encryption helps address key distribution problems • two aspects of this: – distribution of public keys – use of public-key encryption to distribute secret keys
 Distribution of Public Keys • can be considered as using one of: – public announcement – publicly available directory – public-key authority – public-key certificates
Distribution of Public Keys • can be considered as using one of: – public announcement – publicly available directory – public-key authority – public-key certificates
 Public Announcement • users distribute public keys to recipients or broadcast to community at large – eg. append PGP keys to email messages or post to news groups or email list • major weakness is forgery – anyone can create a key claiming to be someone else and broadcast it – until forgery is discovered can masquerade as claimed user
Public Announcement • users distribute public keys to recipients or broadcast to community at large – eg. append PGP keys to email messages or post to news groups or email list • major weakness is forgery – anyone can create a key claiming to be someone else and broadcast it – until forgery is discovered can masquerade as claimed user
 Publicly Available Directory • Registering keys with a public directory – directory must be trusted entity or organization – contains {name, public-key} entries – is periodically published and accessed electronically – participants register securely with directory – participants can replace key at any time • still vulnerable to tampering or forgery – adversary succeeds in obtaining the private key of the directory authority – could tamper with the records kept by the authority.
Publicly Available Directory • Registering keys with a public directory – directory must be trusted entity or organization – contains {name, public-key} entries – is periodically published and accessed electronically – participants register securely with directory – participants can replace key at any time • still vulnerable to tampering or forgery – adversary succeeds in obtaining the private key of the directory authority – could tamper with the records kept by the authority.
 Public-Key Authority • improve security by tightening control over distribution of keys from directory • has properties of directory • and requires users to know public key for the directory • then users interact with directory to obtain any desired public key securely – does require real-time access to directory when keys are needed
Public-Key Authority • improve security by tightening control over distribution of keys from directory • has properties of directory • and requires users to know public key for the directory • then users interact with directory to obtain any desired public key securely – does require real-time access to directory when keys are needed
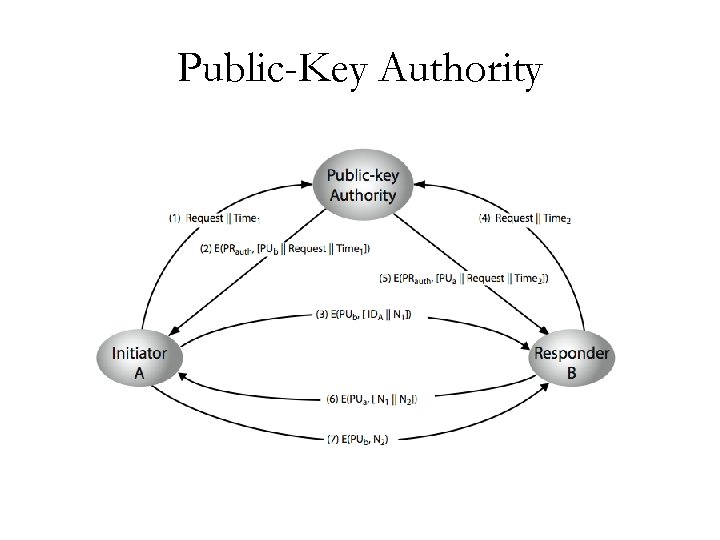 Public-Key Authority
Public-Key Authority
 Public-Key Authority Drawbacks • The public-key authority could be somewhat of a bottleneck in the system • A user must appeal to the authority for a public key for every other user that it wishes to contact. • As before, the directory of names and public keys maintained by the authority is vulnerable to tampering. 11/8/2009 Dr. Monther Aldwairi 8
Public-Key Authority Drawbacks • The public-key authority could be somewhat of a bottleneck in the system • A user must appeal to the authority for a public key for every other user that it wishes to contact. • As before, the directory of names and public keys maintained by the authority is vulnerable to tampering. 11/8/2009 Dr. Monther Aldwairi 8
 Public-Key Certificates • certificates allow key exchange without real-time access to public-key authority • a certificate binds identity to public key – usually with other info such as period of validity, rights of use etc • with all contents signed by a trusted Public-Key or Certificate Authority (CA) • can be verified by anyone who knows the publickey certificate authorities public-key
Public-Key Certificates • certificates allow key exchange without real-time access to public-key authority • a certificate binds identity to public key – usually with other info such as period of validity, rights of use etc • with all contents signed by a trusted Public-Key or Certificate Authority (CA) • can be verified by anyone who knows the publickey certificate authorities public-key
 Requirements • Any participant determine the name and public key of the certificate's owner. • Any participant can verify that the certificate originated from the certificate authority. • Only the certificate authority can create and update certificates. • Any participant can verify the currency of the certificate. 11/8/2009 Dr. Monther Aldwairi 10
Requirements • Any participant determine the name and public key of the certificate's owner. • Any participant can verify that the certificate originated from the certificate authority. • Only the certificate authority can create and update certificates. • Any participant can verify the currency of the certificate. 11/8/2009 Dr. Monther Aldwairi 10
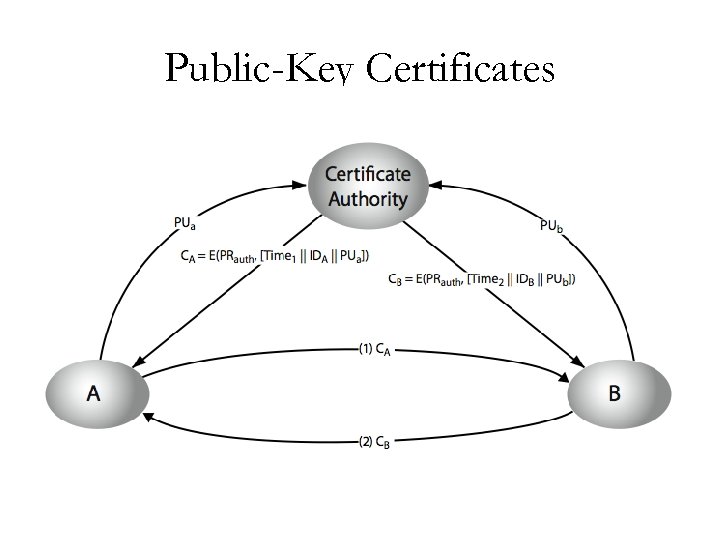 Public-Key Certificates
Public-Key Certificates
 Public-Key Distribution of Secret Keys • • use previous methods to obtain public-key can use for secrecy or authentication but public-key algorithms are slow so usually want to use private-key encryption to protect message contents • hence need a session key • have several alternatives for negotiating a suitable session
Public-Key Distribution of Secret Keys • • use previous methods to obtain public-key can use for secrecy or authentication but public-key algorithms are slow so usually want to use private-key encryption to protect message contents • hence need a session key • have several alternatives for negotiating a suitable session
 Simple Secret Key Distribution • proposed by Merkle in 1979 – A generates a new temporary public key pair – A sends B the public key and their identity – B generates a session key K sends it to A encrypted using the supplied public key – A decrypts the session key and both use (discard keys) • problem is that an opponent can intercept and impersonate both halves of protocol – adversary who can intercept messages and then either relay the intercepted message or substitute another message
Simple Secret Key Distribution • proposed by Merkle in 1979 – A generates a new temporary public key pair – A sends B the public key and their identity – B generates a session key K sends it to A encrypted using the supplied public key – A decrypts the session key and both use (discard keys) • problem is that an opponent can intercept and impersonate both halves of protocol – adversary who can intercept messages and then either relay the intercepted message or substitute another message
 Man in the Middle Attack • A generates a public/private key pair {PUa, PRa} and transmits a message intended for B consisting of PUa and an identifier of A, IDA. • E intercepts the message, creates its own public/private key pair {PUe, PRe} and transmits PUe||IDA to B. • B generates a secret key, Ks, and transmits E(PUe, Ks). • E intercepts the message, and learns Ks by computing D(PRe, E(PUe, Ks)). 11/8/2009 14 • E transmits E(PUa, Ks. Dr. to A. ) Monther Aldwairi
Man in the Middle Attack • A generates a public/private key pair {PUa, PRa} and transmits a message intended for B consisting of PUa and an identifier of A, IDA. • E intercepts the message, creates its own public/private key pair {PUe, PRe} and transmits PUe||IDA to B. • B generates a secret key, Ks, and transmits E(PUe, Ks). • E intercepts the message, and learns Ks by computing D(PRe, E(PUe, Ks)). 11/8/2009 14 • E transmits E(PUa, Ks. Dr. to A. ) Monther Aldwairi
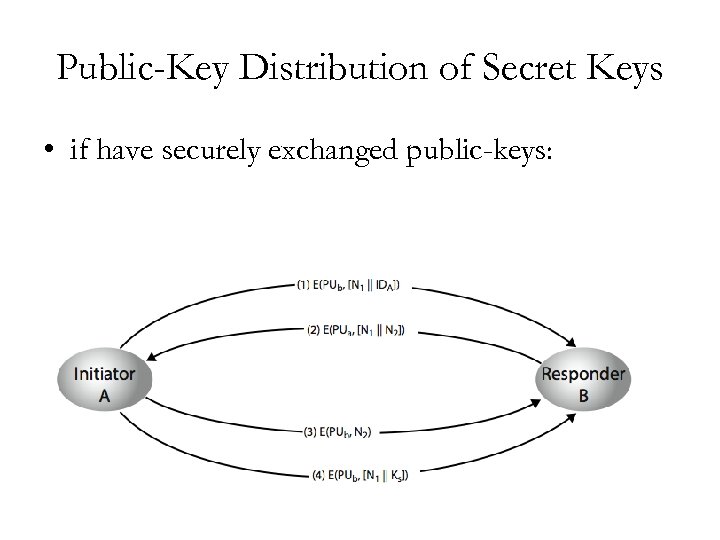 Public-Key Distribution of Secret Keys • if have securely exchanged public-keys:
Public-Key Distribution of Secret Keys • if have securely exchanged public-keys:
 Hybrid Key Distribution • • retain use of private-key KDC shares secret master key with each user distributes session key using master key public-key used to distribute master keys – especially useful with widely distributed users • rationale – performance – backward compatibility
Hybrid Key Distribution • • retain use of private-key KDC shares secret master key with each user distributes session key using master key public-key used to distribute master keys – especially useful with widely distributed users • rationale – performance – backward compatibility
 Diffie-Hellman Key Exchange • first public-key type scheme proposed • by Diffie & Hellman in 1976 along with the exposition of public key concepts – note: now know that Williamson (UK CESG) secretly proposed the concept in 1970 • is a practical method for public exchange of a secret key • used in a number of commercial products
Diffie-Hellman Key Exchange • first public-key type scheme proposed • by Diffie & Hellman in 1976 along with the exposition of public key concepts – note: now know that Williamson (UK CESG) secretly proposed the concept in 1970 • is a practical method for public exchange of a secret key • used in a number of commercial products
 Diffie-Hellman Key Exchange • a public-key distribution scheme – cannot be used to exchange an arbitrary message – rather it can establish a common key – known only to the two participants • value of key depends on the participants (and their private and public key information) • based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy • security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
Diffie-Hellman Key Exchange • a public-key distribution scheme – cannot be used to exchange an arbitrary message – rather it can establish a common key – known only to the two participants • value of key depends on the participants (and their private and public key information) • based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy • security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
 Discrete Logarithms • a primitive root of a prime number p as one whose powers modulo p generate all the integers from 1 to p-1 – For any integer b and a primitive root a of prime number p, we can find a unique exponent i such that – b ≡ ai (mod p) where 0 ≤ i ≤(p-1) • The exponent i is referred to as the discrete logarithm of b for the base a, mod p. – dloga, p (b)= i 11/8/2009 Dr. Monther Aldwairi 19
Discrete Logarithms • a primitive root of a prime number p as one whose powers modulo p generate all the integers from 1 to p-1 – For any integer b and a primitive root a of prime number p, we can find a unique exponent i such that – b ≡ ai (mod p) where 0 ≤ i ≤(p-1) • The exponent i is referred to as the discrete logarithm of b for the base a, mod p. – dloga, p (b)= i 11/8/2009 Dr. Monther Aldwairi 19
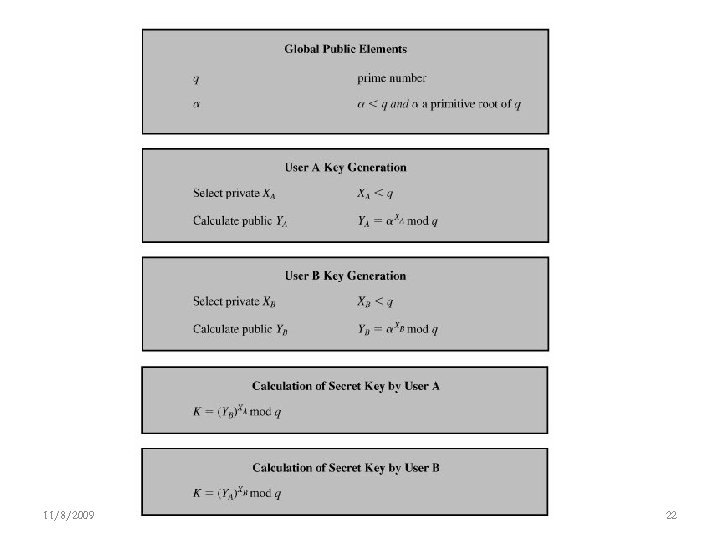
 Diffie-Hellman Setup • all users agree on global parameters: – large prime integer or polynomial q – α being a primitive root mod q • each user (eg. A) generates their key – chooses a secret key (number): x. A < q x. A – compute their public key: y. A = α mod q • each user makes public that key y. A
Diffie-Hellman Setup • all users agree on global parameters: – large prime integer or polynomial q – α being a primitive root mod q • each user (eg. A) generates their key – chooses a secret key (number): x. A < q x. A – compute their public key: y. A = α mod q • each user makes public that key y. A
 Diffie-Hellman Key Exchange • shared session key for users A & B is KAB: x. A. x. B KAB = α mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) • KAB is used as session key in private-key encryption scheme between Alice and Bob • if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys • attacker needs an x, must solve discrete log
Diffie-Hellman Key Exchange • shared session key for users A & B is KAB: x. A. x. B KAB = α mod q x. B = y. A mod q (which B can compute) x. A = y. B mod q (which A can compute) • KAB is used as session key in private-key encryption scheme between Alice and Bob • if Alice and Bob subsequently communicate, they will have the same key as before, unless they choose new public-keys • attacker needs an x, must solve discrete log
 11/8/2009 Dr. Monther Aldwairi 22
11/8/2009 Dr. Monther Aldwairi 22
 Security of the Diffie-Hellman • An adversary only has the following ingredients to work with: q, α, YA, and YB. – XA and XB are private – Calculate discrete logarithm to determine the key – XB = dloga, q (YB) • The security of the Diffie-Hellman key exchange lies in the fact that, – it is relatively easy to calculate exponentials modulo a prime – it is very difficult to calculate discrete logarithms. For large primes, the latter task is considered infeasible. 11/8/2009 Dr. Monther Aldwairi 23
Security of the Diffie-Hellman • An adversary only has the following ingredients to work with: q, α, YA, and YB. – XA and XB are private – Calculate discrete logarithm to determine the key – XB = dloga, q (YB) • The security of the Diffie-Hellman key exchange lies in the fact that, – it is relatively easy to calculate exponentials modulo a prime – it is very difficult to calculate discrete logarithms. For large primes, the latter task is considered infeasible. 11/8/2009 Dr. Monther Aldwairi 23
 Diffie-Hellman Example • users Alice & Bob who wish to swap keys: • agree on prime q=353 and α=3 • select random secret keys: – A chooses x. A=97, B chooses x. B=233 • compute respective public keys: 97 – y. A=3 mod 353 = 40 (Alice) 233 – y. B=3 mod 353 = 248 (Bob) • compute shared session key as: x 97 – KAB= y. B A mod 353 = 248 = 160 x 233 – KAB= y. A B mod 353 = 40 = 160 (Alice) (Bob)
Diffie-Hellman Example • users Alice & Bob who wish to swap keys: • agree on prime q=353 and α=3 • select random secret keys: – A chooses x. A=97, B chooses x. B=233 • compute respective public keys: 97 – y. A=3 mod 353 = 40 (Alice) 233 – y. B=3 mod 353 = 248 (Bob) • compute shared session key as: x 97 – KAB= y. B A mod 353 = 248 = 160 x 233 – KAB= y. A B mod 353 = 40 = 160 (Alice) (Bob)
 Attack Example • An attacker would have available the following information: – q = 353; α = 3; YA = 40; YB = 248 • By brute force, an attacker E can determine the common key by discovering a solution to eqns – 3 a mod 353 = 40 – 3 b mod 353 = 248 – calculate powers of 3 modulo 353, stopping when the result equals either 40 or 248 11/8/2009 Dr. Monther Aldwairi 25
Attack Example • An attacker would have available the following information: – q = 353; α = 3; YA = 40; YB = 248 • By brute force, an attacker E can determine the common key by discovering a solution to eqns – 3 a mod 353 = 40 – 3 b mod 353 = 248 – calculate powers of 3 modulo 353, stopping when the result equals either 40 or 248 11/8/2009 Dr. Monther Aldwairi 25
 Key Exchange Protocols 1. users could create random private/public D-H keys each time they communicate 2. users could create generate a long-lasting private value Xi (for user i) and calculate a public value Yi. – These public values and q and α, are stored in some central directory – user j can access i's public value, calculate KAB • both of these are vulnerable to a meet-in-the. Middle Attack – authentication of the keys is needed
Key Exchange Protocols 1. users could create random private/public D-H keys each time they communicate 2. users could create generate a long-lasting private value Xi (for user i) and calculate a public value Yi. – These public values and q and α, are stored in some central directory – user j can access i's public value, calculate KAB • both of these are vulnerable to a meet-in-the. Middle Attack – authentication of the keys is needed


