Incremental Algorithms for Dispatching in Dynamically Typed Languages

Incremental Algorithms for Dispatching in Dynamically Typed Languages Yoav Zibin Technion—Israel Institute of Technology Joint work with: Yossi (Joseph) Gil (Technion)

Dispatching (in Object-Oriented Languages) n Object o receives message m n n Depending on the dynamic type of o, one implementation of m is invoked Method family Fm = {A, B, E} A dispatching query returns a family member or an error message n Examples: n n n Type Type n A F G I C H return type A (invoke m 1) return type B (invoke m 2) return type E (invoke m 3) Error: message not understood Error: message ambiguous Static typing ensure that these errors never occur

The Dispatching Problem and Variations n n n Encoding of a hierarchy: a data structure representing the hierarchy and the method families which supports dispatching queries. Metrics: space vs. dispatch query time Variations n n n Single vs. Multiple Inheritance Statically vs. Dynamically typed languages Batch vs. Incremental n n Batch (e. g. , Eiffel) the whole hierarchy is given at compile-time Incremental (e. g. , Java) the hierarchy is built at runtime

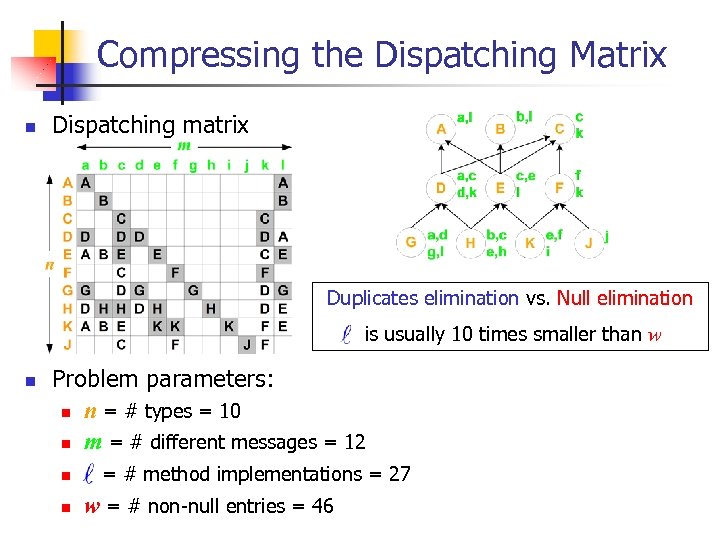Compressing the Dispatching Matrix n Dispatching matrix Duplicates elimination vs. Null elimination is usually 10 times smaller than w n Problem parameters: n n = # types = 10 n m = # different messages = 12 n n = # method implementations = 27 w = # non-null entries = 46

Previous Work n Null elimination (w) n n Selector Coloring, Row Displacement Virtual Function Tables n n n Only for statically typed languages Not suited for Java’s invokeinterface instruction In single inheritance: optimal null elimination In multiple inheritance: tightly coupled with C++ object model Duplicates elimination ( ) n Interval Containment and Type Slicing n n Non-constant dispatch time Compact dispatch Tables (CT) [Vitek & Horspool '94, '96] n n Constant dispatch time! But what is the space complexity?

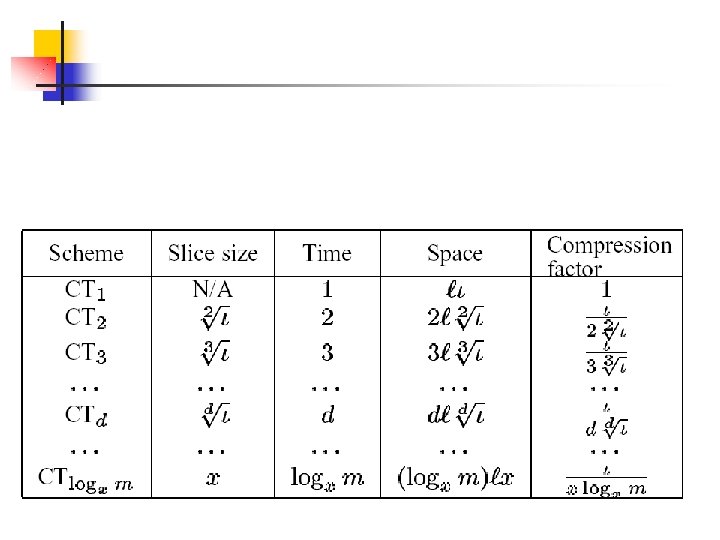
Results n n Analysis of the space complexity of CT Generalize CT into CTd n n n CTd performs dispatching in d dereferencing steps, while using less space (as d increases) CT 1 = Dispatching matrix CT 2 = Vitek & Horspool CT Incremental CTd algorithm in single inheritance Empirical evaluation

Data-set n n Large hierarchies used in real life programs 35 hierarchies totaling 63, 972 types n n 16 single inheritance hierarchies with 29, 162 types 19 multiple inheritance hierarchies with 34, 810 types n n n Still, greatly resemble trees Compression factor of null elimination (w) 21. 6 Compression factor of duplicates elimination ( ) 203. 7

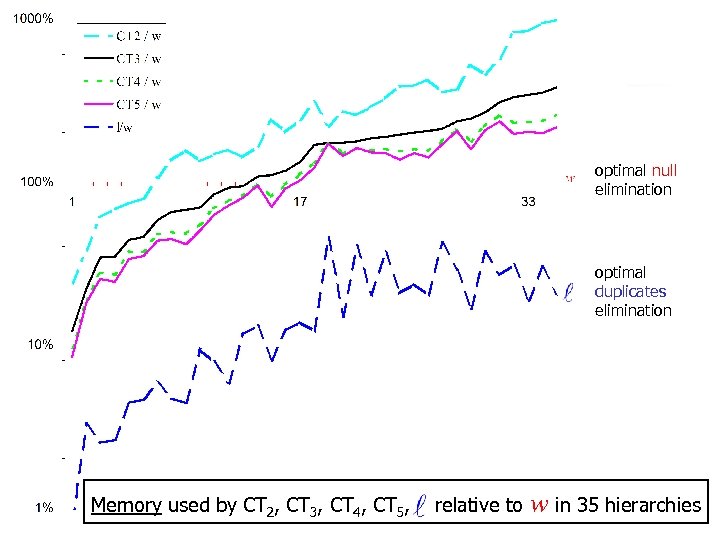optimal null elimination optimal duplicates elimination Memory used by CT 2, CT 3, CT 4, CT 5, relative to w in 35 hierarchies

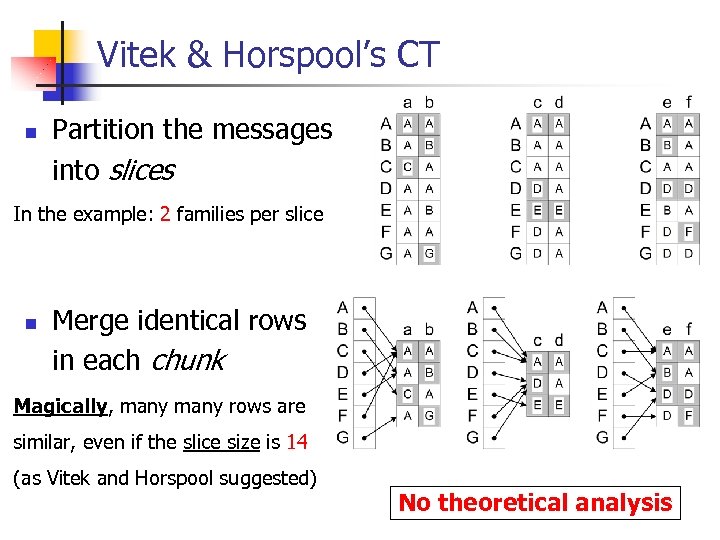Vitek & Horspool’s CT n Partition the messages into slices In the example: 2 families per slice n Merge identical rows in each chunk Magically, many rows are similar, even if the slice size is 14 (as Vitek and Horspool suggested) No theoretical analysis

Our Observations I. It is no coincidence that rows in a chunk are similar The optimal slice size can be found analytically Instead of the magic number 14 III. The process can be applied recursively Details in the next slides

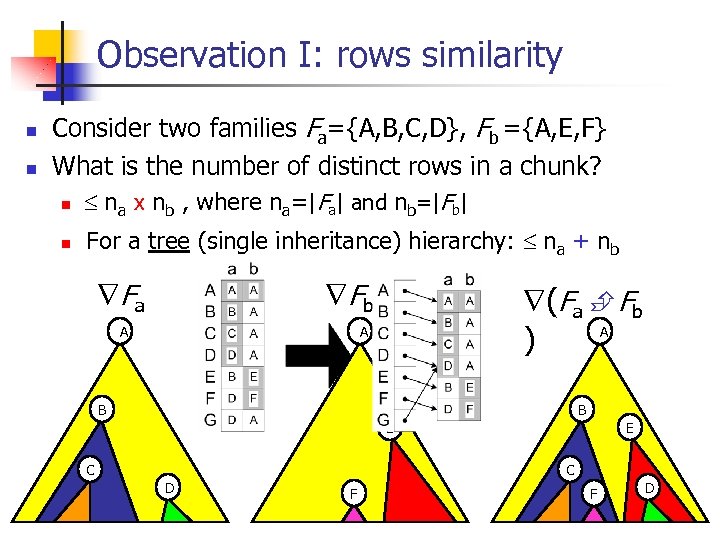Observation I: rows similarity n n Consider two families Fa={A, B, C, D}, Fb ={A, E, F} What is the number of distinct rows in a chunk? n na x nb , where na=|Fa| and nb=|Fb| n For a tree (single inheritance) hierarchy: na + nb Fa Fb A (Fa Fb A ) A B B E C D F F D

Observation II: finding the slice size n n=#types, m=#messages, Let x be slice size. The number of chunks is (m/ x) Two memory factors: n n n = #methods Pointers to rows: decrease with x n(m/x) Size of chunks: increase with x (fewer rows are similar) We bound the size of chunks (using |Fa|+|Fb| idea): x. OPT =

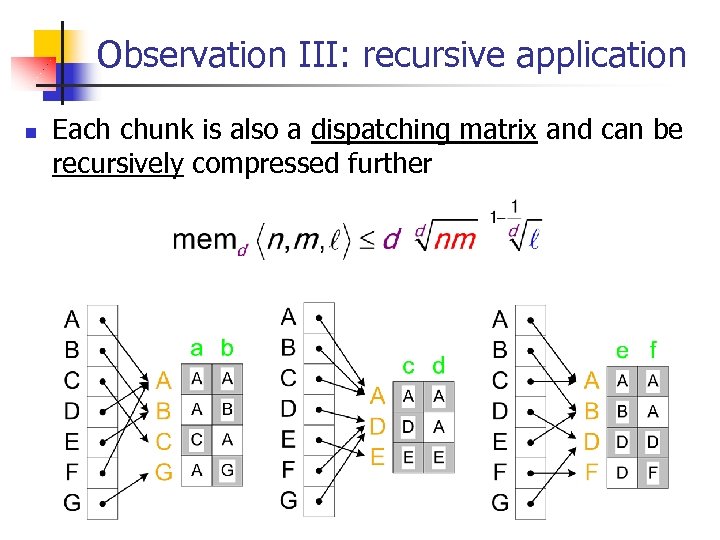Observation III: recursive application n Each chunk is also a dispatching matrix and can be recursively compressed further

Incremental CT 2 n n Types are incrementally added as leaves Techniques: n n Theory suggests a slice size of Maintain the invariant: Rebuild (from scratch) whenever invariant is violated Background copying techniques (to avoid stagnation)

Incremental CT 2 properties n n The space of incremental CT 2 is at most twice the space of CT 2 The runtime of incremental CT 2 is linear in the final encoding size n Idea: Similar to a growing vector, whose size always doubles, the total work is still linear since One of n, m, or always doubles when rebuilding occurs Easy to generalize from CT 2 to CTd

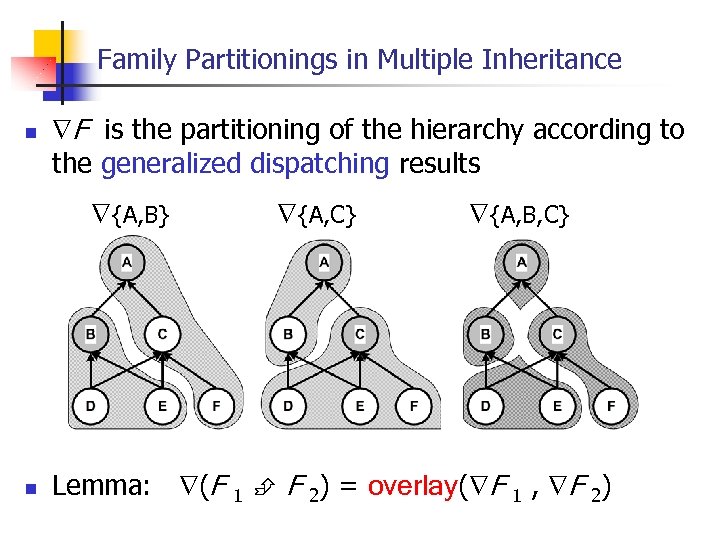Family Partitionings in Multiple Inheritance n F is the partitioning of the hierarchy according to the generalized dispatching results {A, B} n {A, C} {A, B, C} Lemma: (F 1 F 2) = overlay( F 1 , F 2)

Conclusions and Open problems n We gave the first theoretical analysis of space complexity in constant time dispatching techniques n n We described an incremental algorithm for single inheritance which is truly incremental n n Both in single- and multiple- inheritance i. e. , the same complexity as the batch variant Open Problems n An incremental algorithm for multiple inheritance n n There are some subtle issues in this generalization A real implementation n Fine tuning many parameters

The End n Any questions?

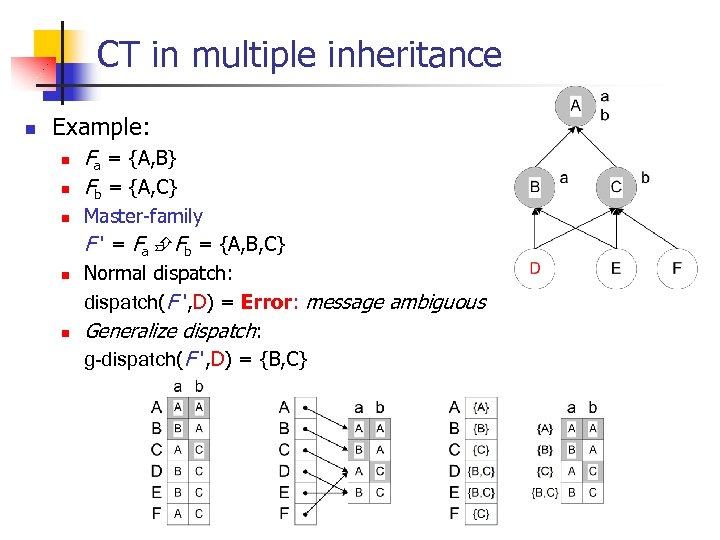CT in multiple inheritance n Example: n n n Fa = {A, B} Fb = {A, C} Master-family F ' = Fa Fb = {A, B, C} Normal dispatch: dispatch(F ', D) = Error: message ambiguous Generalize dispatch: g-dispatch(F ', D) = {B, C}

CT reduction in multiple inheritance n Same as before: n n Partition the method families into slices of size x Create the master-family of each slice Solve the problem (recursively) for the master-families The only difference: n For each master-family F ' = F 1 … Fx create a matrix of size x | F '| for converting the generalizeddispatching results In single inheritance: | F '| = |F '| n In multiple inheritance: n | F '| 2 k |F '| [in the paper] n Conclusion: the space of CTd increases by (2 k)1 -1/d

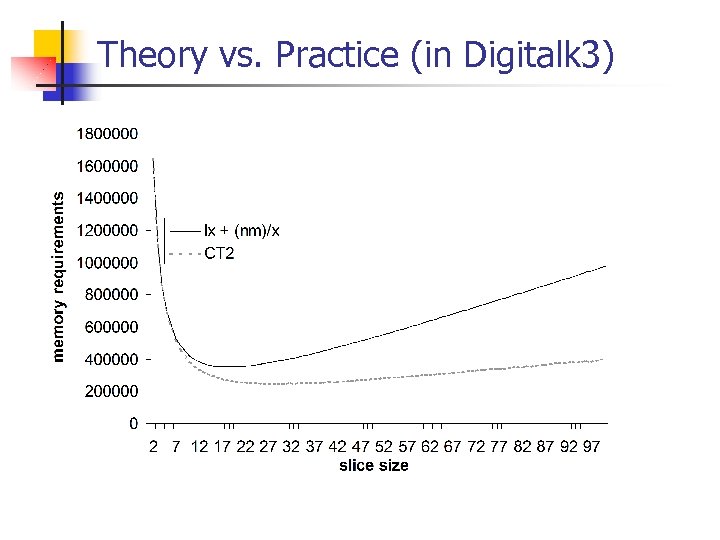Theory vs. Practice (in Digitalk 3)

Our Theoretical Results n CTd performs dispatching in d dereferencing steps n n ) Space in single inheritance: Incremental variant n n n CT 1 = Dispatching matrix CT 2 = Vitek & Horspool CT (with slice size= Twice the space of CTd Insertion time is optimal Space in multiple inheritance increases by a factor of (2 k)1 -1/d n n k is a metric of the complexity of the hierarchy topology In our data set: Median(k )=6. 5, Average(k )=7. 3

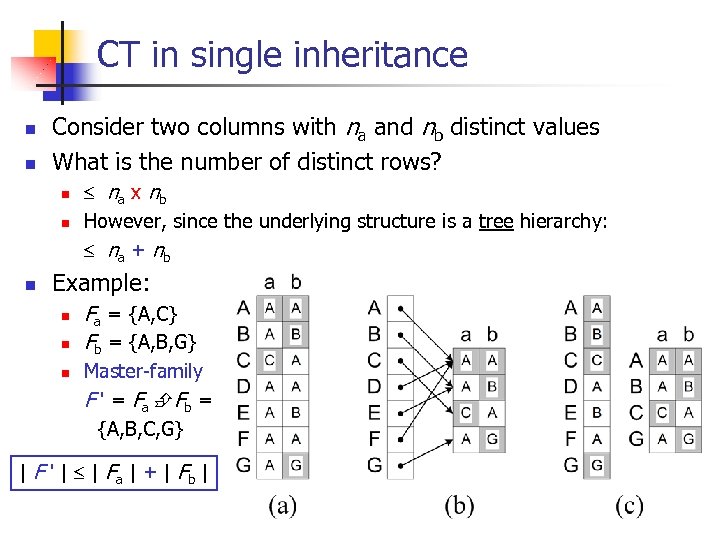CT in single inheritance n n Consider two columns with na and nb distinct values What is the number of distinct rows? n n n na x nb However, since the underlying structure is a tree hierarchy: na + nb Example: n n n Fa = {A, C} Fb = {A, B, G} Master-family F ' = Fa Fb = {A, B, C, G} | F ' | | Fa | + | Fb |

CT reduction n Partition the method families into slices of size x Create the master-family of each slice n Solve the dispatching problem (recursively) for the master-families n (since methods can only “disappear” during the union) n For each master-family F ' = F 1 … Fx create a matrix of size x |F '| for converting the results The size of all matrices is

Some math… n The costs of the CT reduction are n n An extra dereferencing step at runtime The matrices whose size n Then: n And:

Incremental CT 2 in single inheritance n The matrices created in the CT reduction are dispatching matrices n “Easy” to maintain a dispatching matrix incrementally n n A new type copies the row of its parent Overrides the entries of redefined methods Perhaps extends the row to accommodate for new messages The cost: an array overflow check n Catch: how to determine x (the slice size)? n Theory suggests: n We maintain: Otherwise, rebuild everything from scratch!

Incremental CT 2 properties n n Lemma 1: the space of incremental CT 2 is at most twice the space of CT 2 (which is ) Lemma 2: the runtime of incremental CT 2 is linear in the final encoding size n Let be the problem parameters when rebuilding for the ith time. The cost of the ith rebuilding is n Lemma 3: n Lemma 4: n Easy to generalize from CT 2 to CTd Similar to a growing vector