Income Elasticity Normal Goods Elasticity Elasticity Income

Income Elasticity (Normal Goods) Elasticity

Elasticity Income Elasticity (Normal Goods) l Elasticity is a measure of how responsive a dependent variable is to a small change in an independent variable(s) l Elasticity is defined as a ratio of the percentage change in the dependent variable to the percentage change in the independent variable l Elasticity can be computed for any two related variables

Income Elasticity can be computed to show the effects of: (Normal Goods) l a change in price on the quantity demanded [ “a change in quantity demanded” is a movement on a demand function] l a change in income on the demand function for a good l a change in the price of a related good on the demand function for a good l a change in the price on the quantity supplied l a change of any independent variable on a dependent variable

Income Elasticity (Normal Goods) “Own” Price Elasticity

l Income Elasticity Sometimes called “price elasticity” (Normal Goods) l can be computed at a point on a demand function or as an average [arc] between two points on a demand function l ep, h, e are common symbols used to represent price l elasticity Price elasticity [ep] is related to revenue l “How will a change in price effect the total revenue? ” is an important question.

Income Elasticity as a measure of responsiveness (Normal Goods) l The “law of demand” tells us that as the price of a good increases the quantity that will be bought decreases but does not tell us by how much. l ep [“own”price elasticity] is a measure of that information] l “If you change price by 5%, by what percent will the quantity purchased change?

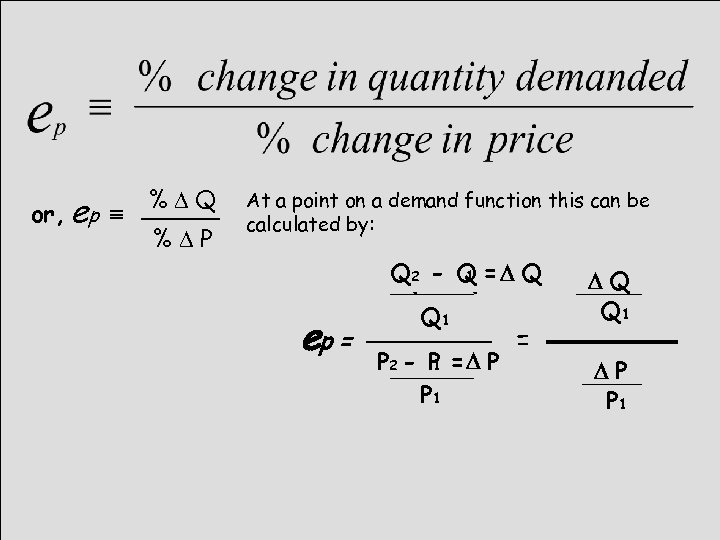or, ep º %DQ %DP At a point on a demand function this can be calculated by: ep = Q 22 - Q = D Q 1 Q - Q 1 P 2 P = D P - - P 1 1 P 1 = DQ Q 1 DP P 1

+2 DQ ep = [2/3 =. 66667] 3 Q 1 = DP -2 P 1 7 % DQ = 67% % DP = -28. 5% [-2/7=-. 28571] Price decreases from $7 to $5 Px P 1 = $7 P 2 = $5 A D P = -2 The “own” price elasticity of demand at a price of $7 is -2. 3 P 2 - P 1 = 5 - 7 = D P = -2 D Q = +2 . [rounded] This is “point” price elasticity. It is calculated at a point on a demand function. It is not influenced by the direction or magnitude of the price change. B Q 1 = 3 = -2. 3 Q 2 = 5 Q 2 - Q 1 = 5 - 3 = D Q = +2 D There is a problem! If the price changes from $5 to $7 the coefficient of elasticity is different! Qx/ut

ep = DQ -2 [-2/5 = -. 4] Q 5 1 = +2 DP % DQ = -40% % DP = 40% = 1 [this is called “unitary elasticity] [+2/5 =. 4] P 5 1 When the price increases from $5 to $7, the ep = -1 [“unitary”] In the previous slide, when the price decreased from $7 to $5, The point price elasticity is different at every point! There is an easier way! Px P 2 = $7 P 1 = $5 A ep = -2. 3 D P = +2 B D Q = -2 Q 2 = 3 ep = -2. 3 Q 1= 5 ep = -1 D Qx/ut

By rearranging terms An easier way! DQ Q 1 D Q 1 P ep = DQ = Q 1 * P 1 D P P 1 ep Q 2= 5 P 2 - P 1 = 5 - 7 = D P = -2 Q 2 - Q 1 = 5 - 3 = D Q = +2 Then, DQ DP = +2 -2 DP * P 1 Q 1 this is the slope of the demand function Given that when: P 1 = $7, Q 1 = 3 P 2 = $5, = DQ this is a point on the demand function = 1 DQ = -1 DP 7 P 1 * Q 1 3 P 1 = $7, = -2. 33 Q 1 = 3 On linear demand functions the slope remains constant so you just put in P and Q This is the slope of the demand Q = f(P)

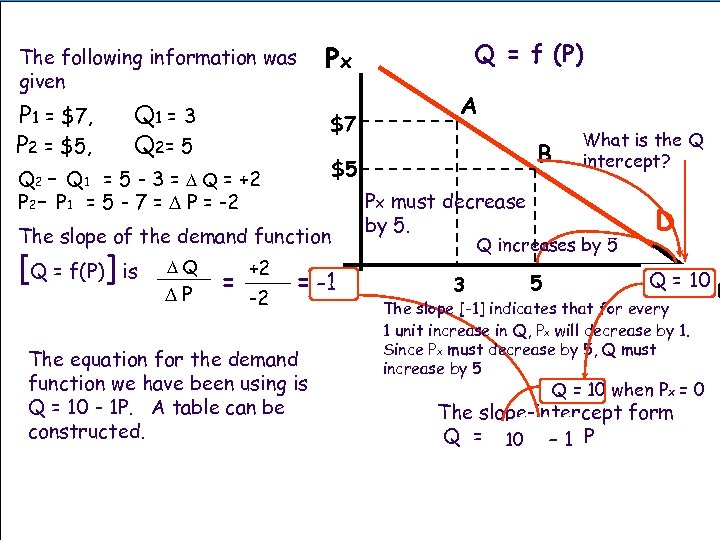The following information was given P 1 = $7, P 2 = $5, Q 1 = 3 Q 2= 5 $7 The slope of the demand function DQ DP = +2 -2 A B $5 Q 2 - Q 1 = 5 - 3 = D Q = +2 P 2 - P 1 = 5 - 7 = D P = -2 [Q = f(P)] is Q = f (P) Px = -1 The equation for the demand function we have been using is Q = 10 - 1 P. A table can be constructed. Px must decrease by 5. What is the Q intercept? Q increases by 5 3 5 D / Q = 10 Qx ut The slope [-1] indicates that for every 1 unit increase in Q, Px will decrease by 1. Since Px must decrease by 5, Q must increase by 5 Q = 10 when Px = 0 The slope-intercept form Q = a 10+ - 1 P m

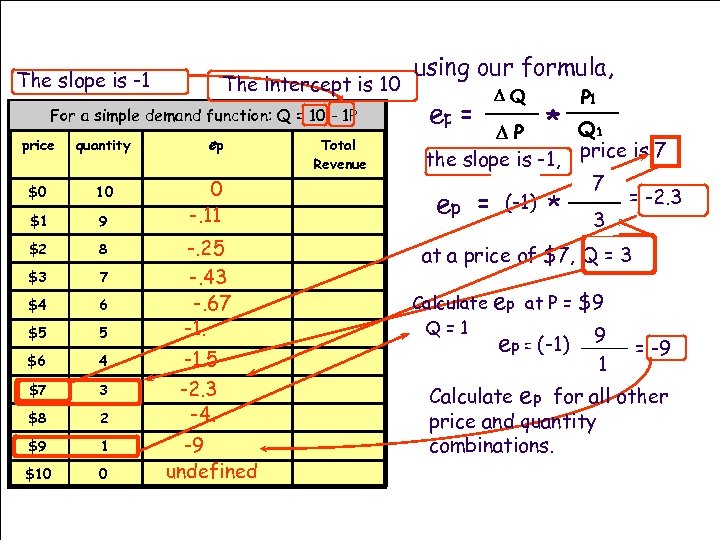The slope is -1 The intercept is 10 For a simple demand function: Q = 10 - 1 P price quantity $0 10 $1 9 $2 8 $3 7 $4 6 $5 5 $6 4 $7 3 $8 2 $9 1 $10 0 ep 0 -. 11 -. 25 -. 43 -. 67 -1. 5 -2. 3 -4. -9 undefined Total Revenue using our formula, ep = DQ P 1 D P * Q 1 the slope is -1, price is 7 P 7 1 DQ ep = (-1) * Q 1 = -2. 3 3 DP at a price of $7, Q = 3 Calculate Q=1 ep at P = $9 ep = (-1) 9 1 = -9 Calculate ep for all other price and quantity combinations.

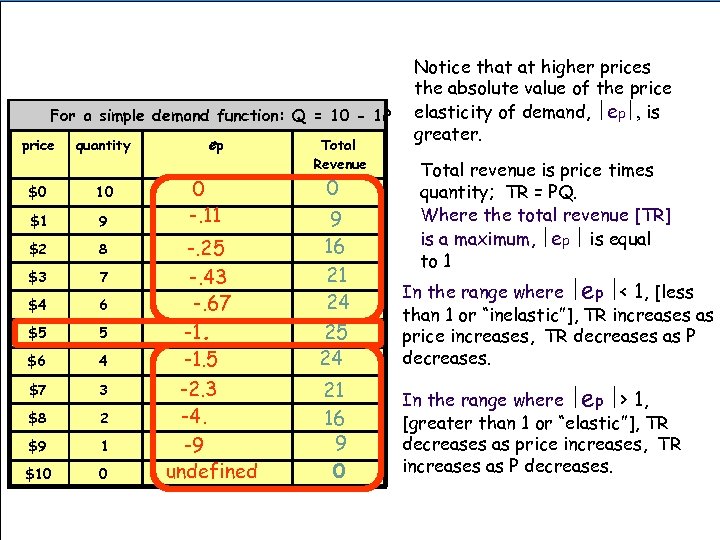For a simple demand function: Q = 10 - 1 P price quantity $0 10 $1 9 $2 8 $3 7 $4 6 $5 5 $6 4 $7 3 $8 2 $9 1 $10 0 ep 0 -. 11 -. 25 -. 43 -. 67 -1. 5 -2. 3 -4. -9 undefined Total Revenue 0 Notice that at higher prices the absolute value of the price elasticity of demand, ½ep½, is greater. Total revenue is price times quantity; TR = PQ. Where the total revenue [TR] is a maximum, ½ep ½ is equal to 1 9 16 21 24 25 24 In the range where ½ep ½< 1, [less than 1 or “inelastic”], TR increases as price increases, TR decreases as P decreases. 21 16 9 0 In the range where ½ep ½> 1, [greater than 1 or “elastic”], TR decreases as price increases, TR increases as P decreases.

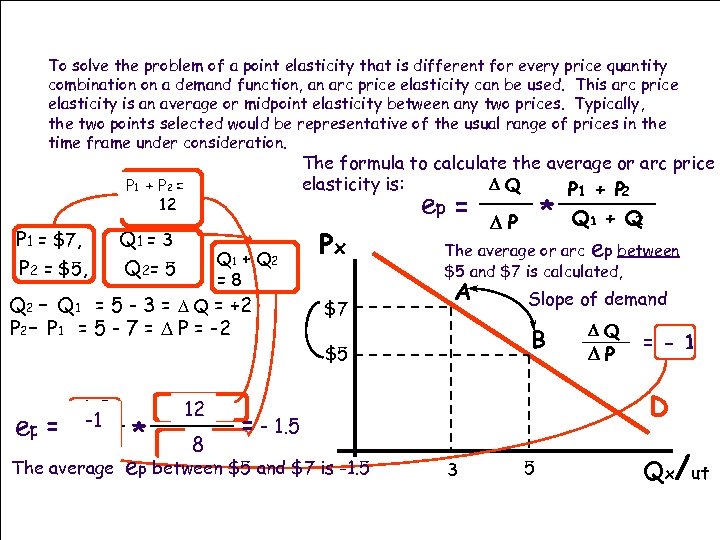To solve the problem of a point elasticity that is different for every price quantity combination on a demand function, an arc price elasticity can be used. This arc price elasticity is an average or midpoint elasticity between any two prices. Typically, the two points selected would be representative of the usual range of prices in the time frame under consideration. The formula to calculate the average or arc price elasticity is: DQ P 1 + P 2 ep = * P 1 + P 2 = 12 P 1 = $7, P 2 = $5, Q 1 = 3 Q 2= 5 Q 1 + Q 2 =8 Q 2 - Q 1 = 5 - 3 = D Q = +2 P 2 - P 1 = 5 - 7 = D P = -2 ep = DQ -1 DP The average * P 1 12 P + 2 Q 1 8 Q + 2 Px $7 Q 1 + Q 2 DP The average or arc ep between $5 and $7 is calculated, A Slope of demand B $5 DP = - 1 D = - 1. 5 ep between $5 and $7 is -1. 5 DQ 3 5 Qx/ut

Given: Q = 120 - 4 P Price Quantity $ 10 $ 25 $ 28 Calculate arc ep TR Calculate the point price on the table. ep at each Calculate the TR at each price on the table. Calculate arc ep at between $10 and $20. Calculate arc ep at between $25 and $28. ep at between $20 and $28. Graph the demand function [labeling all axis and functions], identify which ranges on the demand function are price elastic and which are price inelastic.

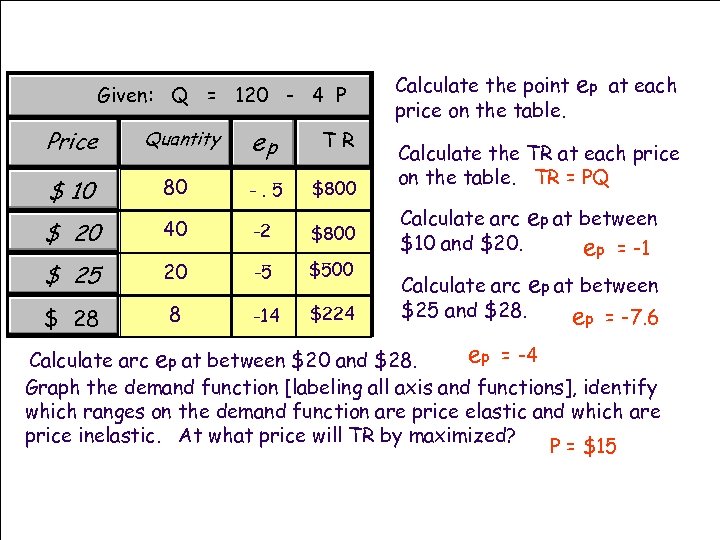Given: Q = 120 - 4 P Price Quantity ep TR $ 10 80 -. 5 $800 $ 20 40 -2 $800 $ 25 20 -5 $500 $ 28 8 -14 $224 Calculate the point price on the table. ep at each Calculate the TR at each price on the table. TR = PQ Calculate arc ep at between $10 and $20. ep = -1 Calculate arc ep at between $25 and $28. ep = -7. 6 ep = -4 Calculate arc ep at between $20 and $28. Graph the demand function [labeling all axis and functions], identify which ranges on the demand function are price elastic and which are price inelastic. At what price will TR by maximized? P = $15

Graphing Q = 120 - 4 P, TR is a maximum where ep is -1 or TR’s slope = 0 Price When ep is -1 TR is a maximum. When | ep | > 1 [elastic], TR and P move in opposite directions. (P has a negative slope, TR a positive slope. ) 30 The top “half” of the demand function is elastic. | ep | > 1 [elastic] ep = -1 | ep | < 1 When | ep | < 1 [inelastic], TR and P move in the same direction. (P and TR 15 both have a negative slope. ) Arc or average ep is the average elasticity between two point [or prices] point ep is the elasticity at a point or price. TR inelastic 60 120 Q/ut The bottom “half” of the demand function is inelastic. Price elasticity of demand describes how responsive buyers are to change in the price of the good. The more “elastic, ” the more responsive to DP.

Determinants of Price Elasticity l Income Elasticity (Normal Goods) Availability of substitutes [greater availability of substitutes makes a good relatively more elastic] l Portion of the expenditures on the good to the total budget [lower portion tends to increase relative elasticity] l Time to adjust to the price changes [longer time period means there are more adjustment possible and increases relative elasticity l Price elasticity for “brands” is tends to be more elastic than for the category of goods

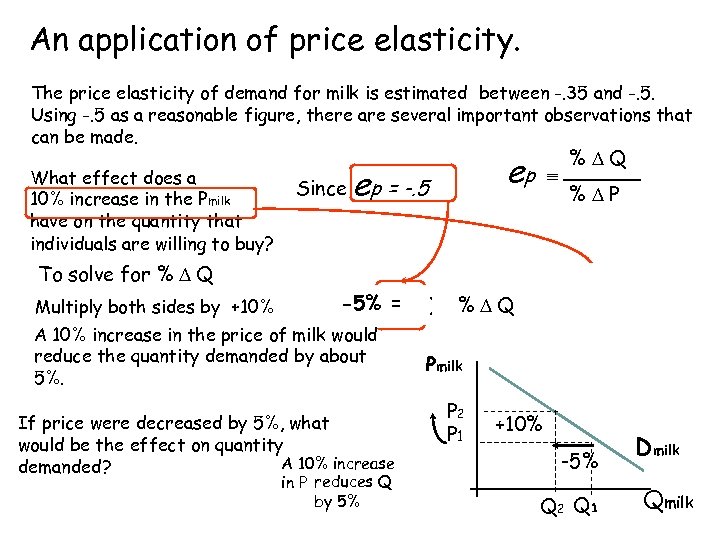An application. Income Elasticity of price elasticity. (Normal Goods) The price elasticity of demand for milk is estimated between -. 35 and -. 5. Using -. 5 as a reasonable figure, there are several important observations that can be made. What effect does a 10% increase in the Pmilk have on the quantity that individuals are willing to buy? To solve for % D Q Multiply both sides by +10% Since ep ep = -. 5 e -5% = p ) (+10%)x (-. 5 º A 10% increase in the price of milk would reduce the quantity demanded by about 5%. If price were decreased by 5%, what would be the effect on quantity A 10% increase demanded? in P reduces Q by 5% º %DQ %DP % = D Q x (+10%) %DQ % +10% DP Pmilk P 2 P 1 +10% -5% Q 2 Q 1 Dmilk Qmilk

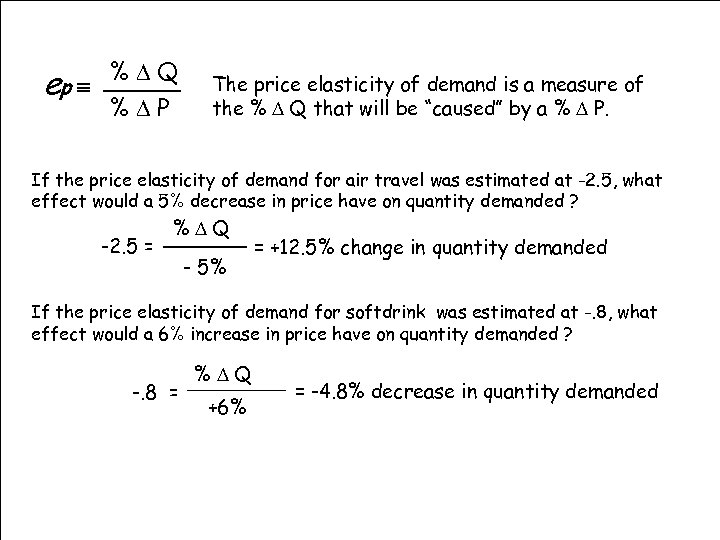%DQ ep º %DP The price elasticity of demand is a measure of the % D Q that will be “caused” by a % D P. If the price elasticity of demand for air travel was estimated at -2. 5, what effect would a 5% decrease in price have on quantity demanded ? -2. 5 = %DQ % 5%P - D = +12. 5% change in quantity demanded If the price elasticity of demand for softdrink was estimated at -. 8, what effect would a 6% increase in price have on quantity demanded ? -. 8 = %DQ %DP +6% = -4. 8% decrease in quantity demanded

If the price elasticity of demand for milk were -. 5, the effects of a price change on total revenue [TR] can also be estimated. Since , %DQ ep º When %DP When |ep| < 1, demand is “inelastic. “ This means that the ê% D Qê < ê% D Pê. Since the % price decrease is greater than the % increase in Q, TR [TR = PQ] will decrease. |ep| < 1, a price decrease will decrease TR; a price increase will increase TR, Price and TR “move in the same direction. ” [inelastic demand with respect to price] When |ep| > 1, demand is “elastic. ” This means that the ê% D Qê > ê% D Pê. When the % price decrease is less than the % increase in Q, TR [TR = PQ] will increase. When |ep| > 1, a price decrease will increase TR; a price increase will decrease TR, price and TR “move in opposite directions. ” [elastic demand wrt price]

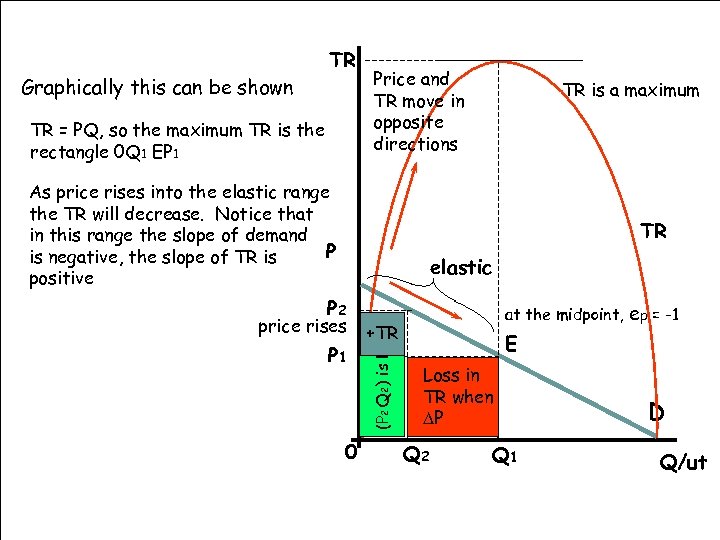Graphically this can be shown TR TR = PQ, so the maximum TR is the rectangle 0 Q 1 EP 1 Price and TR move in opposite directions As price rises into the elastic range the TR will decrease. Notice that in this range the slope of demand P is negative, the slope of TR is positive TR is a maximum TR elastic price rises P 1 0 at the midpoint, ep = -1 +TR (P 2 Q 2) is less P 2 E than in Loss (P 1 Q 1) TR when DP Q 2 Q 1 D Q/ut

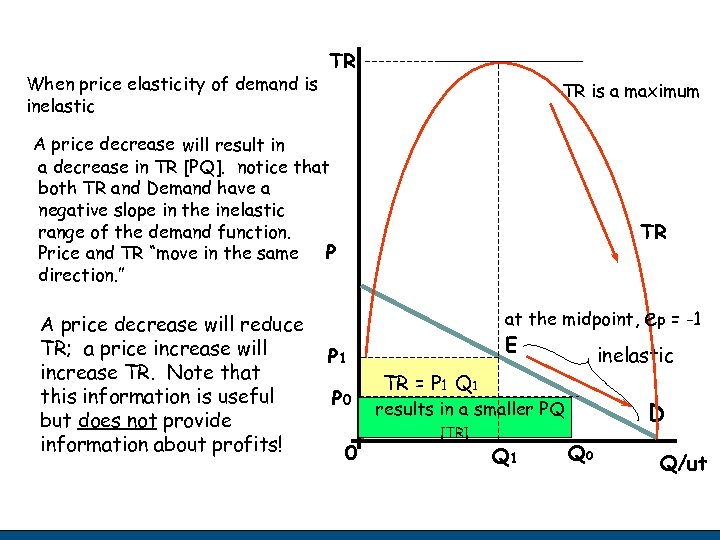When price elasticity of demand is inelastic TR TR is a maximum A price decrease will result in a decrease in TR [PQ]. notice that both TR and Demand have a negative slope in the inelastic range of the demand function. Price and TR “move in the same P direction. ” A price decrease will reduce TR; a price increase will increase TR. Note that this information is useful but does not provide information about profits! TR at the midpoint, P 1 P 0 0 E inelastic TR = P 1 Q 1 [Maximum] results in a smaller PQ [TR] Q 1 ep = -1 D Q 0 Q/ut

“Own” Price Elasticity of Demand l ep will be negative because the demand function is negatively sloped. l A linear demand function will have unitary elasticity at its “midpoint. ” AT THIS POINT TR IS A MAXIMUM! A linear demand function will be more “elastic” at higher prices and tends to be more “inelastic” in the lower price ranges l is a measure of the responsiveness of buyers to changes in the price of the good. Fall '97 Economics 205 Principles of Microeconomics Slide 24

Examples l Goods that are relatively price elastic l lamb, restaurant meals, china/glassware, jewelry, air travel [LR], new cars, Fords in the long run, |ep| tends to be greater Goods that are relatively price inelastic l l electricity, gasoline, eggs, medical care, shoes, milk in the short run, |ep| tends to be less Fall '97 Economics 205 Principles of Microeconomics Slide 26

Reference: Principles of Economics, 6/e by Karl Cas, Ray Fair Slides prepared by: Fernando Quijano and Yvonn Quijano Fall '97 Economics 205 Principles of Microeconomics Slide 27