Improved results for a memory allocation problem Leah

Improved results for a memory allocation problem Leah Epstein University of Haifa Israel Rob van Stee University of Karlsruhe Germany WADS 2007 WAOA 2007

Background Allocate memory to parallel processors n Goals: n – Each processor has sufficient memory – Not too much memory is wasted

Background Problem: memory requirement may vary over time n If each processor can access only one memory, this is inefficient n If all processors share a single memory, there is heavy contention n

Suggested model Chung et al. [SPAA 2004] suggest a new architecture n Each memory may be accessed by at most two processors n This avoids the mentioned problems n

Bin packing They abstract this problem as a bin packing problem n Bins = memories n Items = memory requirements of processors n Thus, items may be larger than 1 n

Bin packing Items may be split and distributed among more than one bin n Condition: each bin contains at most two parts of items n Corresponds to: each memory may be accessed by at most two processors n We also consider the model where each bin may contain k parts of items n

Bin packing Processor Requirement 1 2 3 4 5 Bins Assignment 1, 2 3, 4, 5 1

Notes There may be many bins which are not full n An item may be split more than once n No upper bound on how often each item is split n

Results n Chung et al. [SPAA 2004]: – (k=2) NP-hardness – (k=2) 3/2 -approximation n Epstein & v. S [WADS 2007]: – (k=2) 7/5 -approximation – For general k: n Next Fit is (2 -1/k)-approximation n NP-hardness in the strong sense

Results Epstein & v. S [WAOA 2007]: n A polynomial time approximation scheme (PTAS) for every (constant) k – For every constant >0, a polynomial time algorithm that uses at most 1+ times the minimal number of bins – at most OPT additional bins of size 1

Results Epstein & v. S [WAOA 2007]: n A dual approximation scheme for every (constant) k – For every constant >0, a polynomial time algorithm that uses bins of size 1+ – Larger bins, but no additional bins

Next Fit in this context If current bin contains k parts of items or is fulll, open a new bin n Put as much as possible of the current item in the current bin n Open additional bin(s) if needed (for large items) n

Next Fit: lower bound Mk -1 n M (k -1) One item of size Mk-1 – Next Fit uses Mk-1 bins n M (k-1)k very small items – Next Fit puts k items in one bin, uses M (k-1) bins

Next Fit: lower bound Mk -1 M (k -1) Mk Optimal solution needs only Mk bins n Ratio: (M (2 k-1)-1) /Mk 2 – 1/k n

Next Fit: upper bound Block = set of full bins, followed by a bin with k items n Each bin >1 in a block was opened because the previous one was full n

Weights Weight of item with size s = s /k n There at least s parts of item with size s in any packing n n OPT is at least the total weight of all the items

Next Fit: upper bound Consider last bin in a block (not the last block) n Has k items, so at least k -1 items of weight 1/k (these items are not split!) n Block has 1 bin, then k such items n Else, consider all items in block except the k -1 last items n

Next Fit: upper bound n S = all items in block except the k -1 last items n How many items are in S ? Unknown! n What is the minimal weight of S ? n Weight = , minimized for single item

Next Fit: upper bound n S = all items in block except the k -1 last items n For block of size b, total size of items in S is strictly more than b -1 n Total weight is then at least b /k n Weight in block at least b /k +(k -1)/k n Note: also true for block of size 1

The last block Only one bin: weight at least 1/k (has at least one item) n b >1 bins: weight at least b /k n Let size of block i be bi , then Next Fit uses bins n We know that OPT is at least the total weight n

Next Fit: upper bound n n Let m be the amount of blocks Also, OPT > NF – m (in each block, at most one bin is not completely full)

Next Fit: upper bound Combining this we find

This talk We only discuss the algorithms for k=2 n General properties n PTAS n Dual PTAS n 23

Representation of solutions A solution can be seen as a graph n Vertices = items n An edge between two items = Parts of these two items share a bin n – A loop means that a bin contains just one part of an item n We can assume a forest (with loops) – Cycles can be easily removed without changing the cost (Chung et al. , 2004).

Example Items:

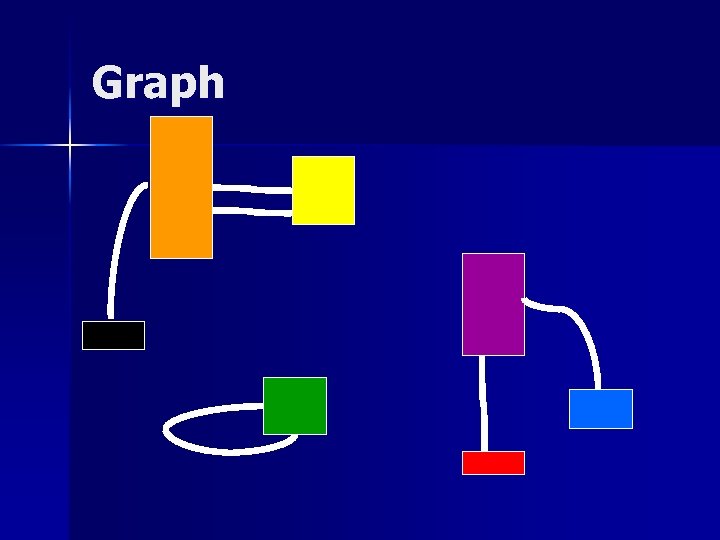
Graph

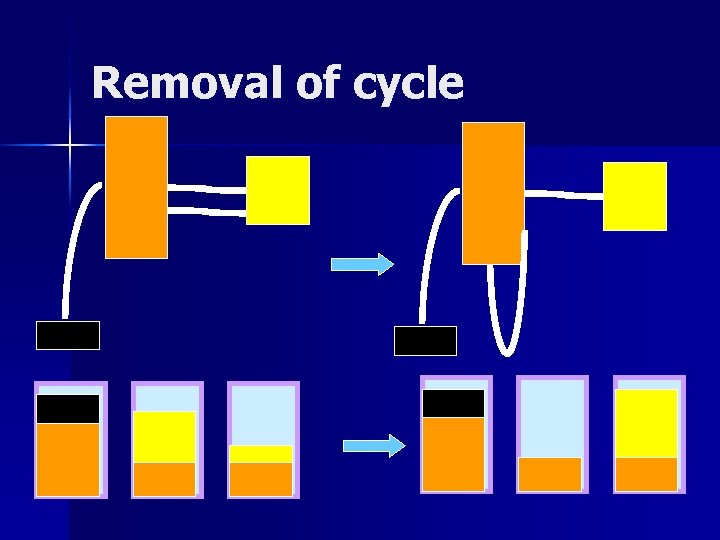
Removal of cycle

Additional properties n n There exists an optimal packing forest where all items of size in (0, 1/2] are leaves or singletons If the forest representation is minimal (no tree can be split) then a packing is implied from the tree – – – Can be done iteratively Singletons are packed into separate bins A leaf is packed with a maximum amount of its neighbor, and removed from the forest

(Different) example 1. 5 0. 4 0. 9 0. 2 1 0. 3 0. 2

Packing process 1 0. 8 0. 6 0. 9 0. 4 0. 3 0. 1 0. 2

PTAS for k=2 n We would like to use standard methods such as – Linear grouping and rounding – Enumeration of patterns n But – Patterns are trees – Items sizes are not bounded from above

New tricks Optimal packing is adapted in order to make it possible to imitate it n Trees are “truncated” n – Partitioned into smaller trees n Large items are truncated – Partitioned into several items that are still large, but bounded n The last two adaptations increase the number of bins by a factor of 1+

Trying all trees n Type of a tree is (j, E) – j is number of edges – E is set of j-1 edges (so that it is a tree) n Pattern = type plus vector of length j – Element i in the vector indicates group of node i Constant number of patterns n Only question: how many of each? n

Dual PTAS for k=2 (briefly) We use an integer parameter K, based on . n Items can be rounded down to a sizes of the form i/K n We round some non-zero sizes into zero! n By scaling, we get items of integer sizes, and a bin size K n

Cutting There is no reason to cut items at noninteger point n For each item size (at most K), we define cutting patterns n We “guess” how to cut the input items n – Using enumeration

Finding a solution n We use a layered graph to find an optimal packing for each option – If the cutting was applied, the problem becomes much easier – However, we did not cut items larger than the bin size – We cut a piece off each one of them, but do not decide on all cutting points n n The best (smallest number of bins) option is chosen Increasing items back to original sizes increases bins slightly

Open problems PTAS, dual PTAS for non-constant k n (FPTAS or dual FPTAS are most likely impossible since the problem is strongly NP-hard for every constant value of k) n Generalize 7/5 -approximation for larger k n

7/5 -approximation We show an approximation algorithm for k=2 (at most two parts of items per bin allowed) n First it sorts the items n Then it packs them, starting with the most difficult ones: size between ½ and 1 n We use Next Fit as a subroutine n

Step 1: Sorting n Items of size at most ½ are small – Sort them in order of increasing size n Items larger than 1 are large – Sort them in order of decreasing size n Other items are medium-sized – Sort them in order of decreasing size – We pack these items first

Step 2: medium-sized items n Pack medium-sized items one by one: – If current item fits in one bin with the smallest unpacked small item, pack them together – Else, pack current item together with two largest unpacked small items in two bins

Step 3: all small items are packed We do this until we run out of either the medium-sized or the small items n If all small items are packed, use Next Fit on rest, start with medium-sized items n

Step 4: some small items remain Pack each small item in its own bin n Pack large items into these bins using Next Fit n Still use ordering from before: n – Largest large items first – Smallest small items first

Step 5: small items left We have now run out of either the large or the small items n If bins with small items remain, repack these items two per bin n

Step 6: large items left n Pack remaining large items using Next Fit

Upper bound n We use the same weight definition as before: weight of item with size s is We know that OPT is at least the total weight n How much weight do we pack in a bin? n

Amount of weight packed Step 2: n Pack medium-sized items one by one: – If current item fits in one bin with the smallest unpacked small item, pack them together. Weight ½+½ = 1 – Else, pack current item together with two largest unpacked small items in two bins. Three items of weight ½ in two bins: ¾

Amount of weight packed Step 3: n If all small items are packed, use Next Fit on rest, start with medium-sized items We assume many small items exist n Then, this step does not occur n

Amount of weight packed Step 4: n Pack each small item in its own bin n Pack large items into these bins using Next Fit n Still use ordering from before: – Largest large items first – Smallest small items first

Amount of weight packed Consider a large item which is packed into g bins n It is packed together with g small items (total weight g /2) n The large item has size strictly more than (g -1)/2, so weight at least g /4 n Average weight per bin = 3/4 n

Amount of weight packed Step 5: n We have now run out of either the large or the small items n If bins with small items remain, repack these items two per bin n Weight: ½ + ½ = 1

Packed weight: summary Step 2: ½+½=1, or 3 times ½ in two bins, average ¾ n Step 4: average ¾ n Step 5: ½+½=1 n Gives upper bound of 4/3! (Since OPT is at least total weight)

However… n There may be only one small item left at the end of Step 5 – „If bins with small items remain, repack these items two per bin“ We may run out of small items in Step 2, so that Step 3 is executed n We may run out of small items in Step 4, so that Step 6 is executed n

Upper bound It turns out that these cases are the most difficult n Proof is a number of pages n Eventually we find an upper bound of 7/5 in all cases n

Open questions n Improve this approximation ratio – We can give a PTAS, but this is much less efficient already for epsilon = 2/5 n Generalize this algorithm for larger k – We have the upper bound of Next Fit, which is 2 -1/k, and a PTAS – Can we improve on Next Fit efficiently?

Thank you!