Implicit Solvation Models Xiaolin Cheng UT ORNL Center for

Скачать презентацию Implicit Solvation Models Xiaolin Cheng UT ORNL Center for

43d569d833963dd8d785fae957387c88.ppt

Количество слайдов: 43

Implicit Solvation Models Xiaolin Cheng UT/ORNL Center for Molecular Biophysics 02/18/2008 Introduction to Molecular Biophysics 1

Water is important Water has importance as a solvent, a solute, a reactant and a biomolecule, structuring proteins, nucleic acids and even cells. Water unique properties: High melting point Water shrinks on melting High viscosity High dielectric constant … … Its unique hydration properties towards biological macromolecules (particularly proteins and nucleic acids) determine their three-dimensional structures, and hence their functions, in solution. In molecular modeling studies, the water environment can be represented either explicitly or implicitly as we will discuss below. http: //en. wikipedia. org/wiki/Water_model Introduction to Molecular Biophysics 2

Water Molecule Structure V-shaped, approximately tetrahedrally arranged, sp 3 -hybridized electron pairs, two of which are bonded with hydrogen atoms leaving the two remaining lone pairs. gaseous water molecule O-H length 0. 95718 Å, H-O-H angle 104. 474° liquid water O-H length 0. 991 Å, H-O-H angle 105. 5° (ab initio) O-D length 0. 970 Å, D-O-D angle 106° (neutron diffraction) These bond lengths and angles are likely to change, due to polarization shifts, in different hydrogen-bonded environments and when the water molecules are bound to solutes and ions. Commonly used molecular models use O-H lengths of between 0. 957 Å and 1. 00 Å and H-O-H angles of 104. 52° to 109. 5°. http: //en. wikipedia. org/wiki/Water_model Introduction to Molecular Biophysics 3

Explicit Water Models A water model is defined by its geometry, together with other parameters such as the atomic charges and Lennard-Jones parameters. Many different models have been proposed; they can be classified by the number of points used to define the model (atoms plus dummy sites), whether the structure is rigid or flexible, and whether the model includes polarization effects. http: //en. wikipedia. org/wiki/Water_model Introduction to Molecular Biophysics 4

Explicit Water Models The simplest water models treat the water molecule as rigid and rely on non-bonded interactions. The electrostatic interaction is modeled using Coulomb's law and the dispersion and repulsion forces using the Lennard. Jones potential. Electrostatic: Lennard-Jones: Note: In most water models, the Lennard-Jones term applies only to the interaction between the oxygen atoms. Introduction to Molecular Biophysics 5

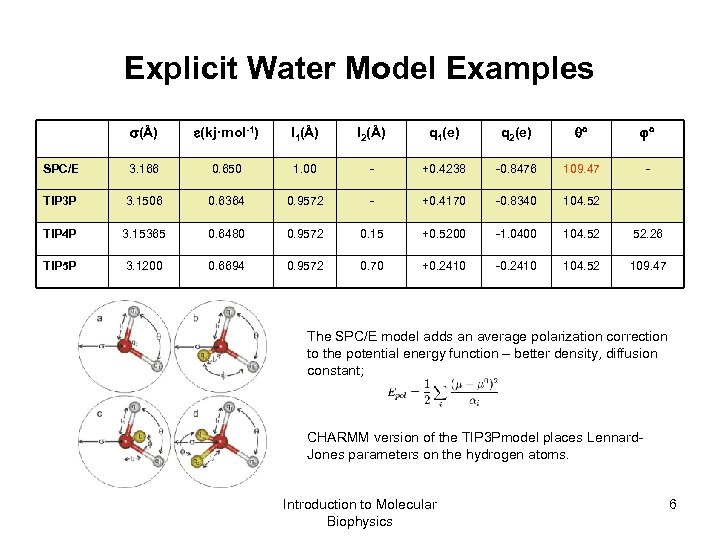Explicit Water Model Examples (Å) (kj·mol-1) l 1(Å) l 2(Å) q 1(e) q 2(e) SPC/E 3. 166 0. 650 1. 00 - +0. 4238 -0. 8476 109. 47 - TIP 3 P 3. 1506 0. 6364 0. 9572 - +0. 4170 -0. 8340 104. 52 TIP 4 P 3. 15365 0. 6480 0. 9572 0. 15 +0. 5200 -1. 0400 104. 52 52. 26 TIP 5 P 3. 1200 0. 6694 0. 9572 0. 70 +0. 2410 -0. 2410 104. 52 109. 47 The SPC/E model adds an average polarization correction to the potential energy function – better density, diffusion constant; CHARMM version of the TIP 3 Pmodel places Lennard. Jones parameters on the hydrogen atoms. Introduction to Molecular Biophysics 6

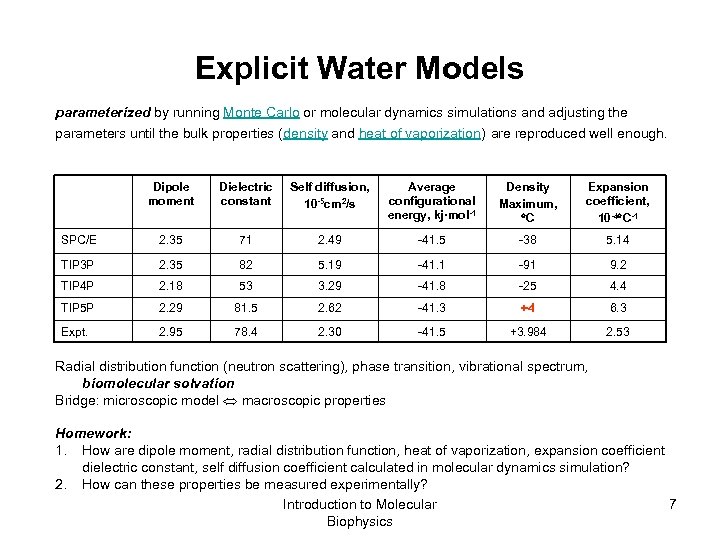Explicit Water Models parameterized by running Monte Carlo or molecular dynamics simulations and adjusting the parameters until the bulk properties (density and heat of vaporization) are reproduced well enough. Dipole moment Dielectric constant Self diffusion, 10 -5 cm 2/s Average configurational energy, kj·mol-1 Density Maximum, C Expansion coefficient, 10 -4 C-1 SPC/E 2. 35 71 2. 49 -41. 5 -38 5. 14 TIP 3 P 2. 35 82 5. 19 -41. 1 -91 9. 2 TIP 4 P 2. 18 53 3. 29 -41. 8 -25 4. 4 TIP 5 P 2. 29 81. 5 2. 62 -41. 3 +4 6. 3 Expt. 2. 95 78. 4 2. 30 -41. 5 +3. 984 2. 53 Radial distribution function (neutron scattering), phase transition, vibrational spectrum, biomolecular solvation Bridge: microscopic model macroscopic properties Homework: 1. How are dipole moment, radial distribution function, heat of vaporization, expansion coefficient dielectric constant, self diffusion coefficient calculated in molecular dynamics simulation? 2. How can these properties be measured experimentally? Introduction to Molecular 7 Biophysics

Explicit Water Models Explicit water models can provide a realistic picture of how biomolecules behave in a biological environment: structured water molecules, solvation, hydrophobic effect… but the large number of water molecules in addition to the biomolecule adds significant computational costs -- the computational cost of a water simulation increases with the number of interaction sites in the water model; when using rigid water models in molecular dynamics, there is an additional cost associated with keeping the structure constrained. Water molecule is a flexible molecule with electronic polarization; nonpolarizable models have been shown to be inherently unable to simultaneously predict certain physical properties, such as melting temperature and the temperature of maximum density. Introduction to Molecular Biophysics 8

Further Readings 0. http: //en. wikipedia. org/wiki/Water_model 1. Jorgensen, W. L. Quantum and statistical mechanical studies of liquids. 10. Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc. 1981, 103, 335 -340. 2. P. Ren and J. W. Ponder, Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation, J. Phys. Chem. B 107, 5933 -5947 (2003) 3. Darden T, Perera L, Li L and Pedersen L. (1999) "New tricks for modelers from the crystallography toolkit: the particle mesh Ewald algorithm and its use in nucleic acid simulations", Structure 7, R 55 -R 60. 4. L. Greengard, V. Rokhlin, J. Comput. Phys. 73 (1987) 325. Introduction to Molecular Biophysics 9

Implicit Solvation Models Explicit Solvent Average Density Implicit Solvent http: //feig. bch. msu. edu/main-research-methodology. html It is possible to construct an implicit solvent model by approximating the medium outside the water-excluded volume as a continuum with electrostatic, entropic, and viscous properties that match water. Introduction to Molecular Biophysics 10

Implicit Solvation Models Consider the ensemble average of property A dependent on only the solute degrees of freedom X Q Integration over the solvent degrees of freedom, and define the potential of mean force W(X) Now the expression for above becomes, where the integration is only on the solute degrees of freedom and solvent effects are accounted implicitly by W(X). The definition of W(X) does not immediately simply the calculation of . But W(X) is available from other sources, such as empirical description of the solvent. Introduction to Molecular Biophysics 11

Implicit Solvation Models The gradient of W(X) with respect to X is the force F(X) exerted on the solute by the solvent averaged over the ensemble of solvent configurations when the solute degrees of freedom fixed at X The function W(X) describes a free energy potential not a mere potential energy – the solvation free energy on the solute due to the solvent averaged over many solvent configurations. It is noteworthy that the solvation free energy is the free energy required to transfer a solute molecule from the “vacuum” (gas phase) to the solvent. Introduction to Molecular Biophysics 12

Implicit Solvation Models An alternative approach, we can write the solvation free energy of the solute in conformation X: where Gnp is the change of solvation free energy in going from nothing to the nonpolar solute and Gelec is the change of free energy in going from the non-polar (uncharged) form of the solute to the polar (charged) form of the solute. Introduction to Molecular Biophysics 13

Nonpolar Solvation The solvation of a non-polar solute in water is disfavored by the disruption of the hydrogen bonding network of water and also by the loss of entropy associated with the fact that water molecules cannot occupy the volume occupied by the solute. The solvation of non-polar solute is however favored by attractive van der Waals interactions between the solute and solvent, even though the van der Waals interactions are usually not as strong as the polar interactions. The non-polar solvation free energy of a solute is proportional to the solvent accessible surface area (SASA) of the solute: where A(X) is the SASA of conformation X, is an adjustable parameter that is interpreted as surface tension. For hydrocarbons ≈ 5 cal/(mol ·Å2) The formulation becomes strictly valid in macroscopic thermodynamics - the creation of a phase boundary between two macscopic phases is associated with a free energy increase proportional to the area of the boundary surface. Introduction to Molecular Biophysics 14

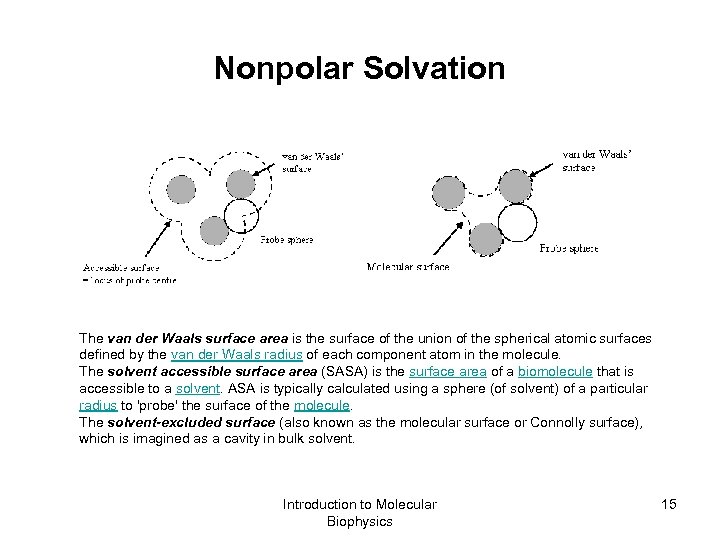Nonpolar Solvation The van der Waals surface area is the surface of the union of the spherical atomic surfaces defined by the van der Waals radius of each component atom in the molecule. The solvent accessible surface area (SASA) is the surface area of a biomolecule that is accessible to a solvent. ASA is typically calculated using a sphere (of solvent) of a particular radius to 'probe' the surface of the molecule. The solvent-excluded surface (also known as the molecular surface or Connolly surface), which is imagined as a cavity in bulk solvent. Introduction to Molecular Biophysics 15

Nonpolar Solvation The solvent accessible surface area (SASA) partially accounts for the hydrophobic effect. The hydrophobic effect is the property that non-polar molecules tend to form intermolecular aggregates in water, an entropic effects arising from solute-imposed constraints on the organization of the water or solvent molecules. At the molecular level, the hydrophobic effect is an important driving force for biological structures and responsible for protein folding, protein-protein interactions, formation of lipid bilayer membranes, nucleic acid structures, and protein-small molecule interactions. SASA enjoys many successful applications: solvation energy, binding free energy (MMPB/SA), and protein dynamics (GB/SA) but not accurate can not capture the "specific" distance-dependent interactions; this surface area pertains to the solute, while the hydrophobic effect is entropic in nature and occurs on the side of the solvent. Further readings: Chandler, D. , "Insight Review: Interfaces and the driving force of hydrophobic assembly”, Nature 437, 640 -647 (2005). For a recent discussion, see PNAS, 103, 8331 (2006) Introduction to Molecular Biophysics 16

Polar Solvation Consider the free energy of placing a charge q at the center of a spherical cavity in a solvent. The process of reversibly placing the charge is accomplished by introducing a charging parameter such that q is the charge along the charging process. The solutesolvent potential energy of the system at is The mean force along the charging parameter , - - - +q - - - The charging free energy is therefore given by, The electrostatic potential generated by the solvent charges at the solute charge location, “reaction field” Introduction to Molecular Biophysics 17

Polar Solvation An alternative would be to consider the solvent to be a uniform dielectric medium with dielectric constant (for water = 80). The dielectric is polarized by the charge at the center of the spherical cavity and will produce a reaction field that opposes the electric field produced by the solute charge. The average reaction field < >v, q at generated by the dielectric at the center of the sphere is given by Gauss’s theorem This expression is known as Born model, it gives the charging free energy (hydration energy) of a single ion in a spherical cavity. Introduction to Molecular Biophysics 18

Polar Solvation For the general case of a solute of arbitrary shape with several partial charge sites, the electrostatic free energy is given by, satisfies the Poisson equation analytical solution available for spherical, cylindrical, or planar symmetry Introduction to Molecular Biophysics - - - a - 0 +q - - 19

Poisson-Boltzmann Theory The electrostatic potential related to charge density is given by Poisson’s law _ Mobile ions and the Poisson-Boltzmann equation + + Expand at low-salt concentration _ where, in: 1 + The Tanford and Kirkwood model for protein _ + + out: 2 Introduction to Molecular Biophysics 20

Numerical Solution of PB Numerical solution (FD, BE, FEM) The finite difference formulation: spatial derivatives are approximated using neighboring points. A successive overrelaxation method used to get rapid convergence in solving the linear systems obtained from the finite difference discretization; The boundary element method: utilizes analytical solutions obtained in terms of Green’s functions and discretization on the domain surface (molecular surface); The finite element method: an adaptive multilevel approach based on tetrahedral elements to create a dense mesh to capture the dielectric discontinuity across the molecular surface. Introduction to Molecular Biophysics 21

Numerical Solution of PB Advantages Disadvantages Finite difference and uniform mesh methods • Fast solvers • Low memory overhead • Cartesian mesh • Non-adaptive • Poor solution resolution • Previous parallel methods complicated and inefficient Boundary element methods • Smaller numerical systems • Less efficient solvers • Easier interaction • Only applicable to linear evaluation problem Finite element methods • Highly adaptive • Relatively fast solvers • Previous solver and adaptive methods inadequate • Previous parallel methods complicated and inefficient adapted from Nathan A. Baker’s slides, North Dakota State University, 2003 Introduction to Molecular Biophysics 22

Delphi A Finite Difference Poisson-Boltzmann Solver Del. Phi provides numerical solutions to the Poisson-Boltzmann equation (both linear and nonlinear form) for molecules of arbitrary shape and charge distribution. It has nice features for assigning different dielectric constants to different regions of space and treating systems containing mixed salt solutions. http: //wiki. c 2 b 2. columbia. edu/honiglab_public/index. php/Software: Del. Phi GRASP (Graphical Representation and Analysis of Structural Properties) GRASP is a molecular visualization and analysis program. It is particularly useful for the display and manipulation of the surfaces of molecules and their electrostatic properties. http: //wiki. c 2 b 2. columbia. edu/honiglab_public/index. php/Software: GRASP Introduction to Molecular Biophysics 23

Delphi Introduction to Molecular Biophysics 24

APBS: Adaptive Poisson-Boltzmann Solver APBS is a software package for the numerical solution of the Poisson. Boltzmann equation (PBE), for evaluating the electrostatic properties of nanoscale biomolecular systems. APBS was designed to efficiently evaluate electrostatic properties for such simulations for a wide range of length scales to enable the investigation of molecules with tens to millions of atoms. APBS uses FETK (the Finite Element Tool. Kit) to solve the Poisson-Boltzmann equation numerically. http: //apbs. sourceforge. net/ PMV (Python Molecular Viewer) PMV is a powerful molecular viewer that has a number of customizable features and comes with many pluggable commands ranging from displaying molecular surfaces to advanced volume rendering. http: //mgltools. scripps. edu/ Introduction to Molecular Biophysics 25

APBS Introduction to Molecular Biophysics 26

Diverse Applications 1. surface potentials, solvent transfer energies, binding energies, p. Ka shifts, and effective dielectric constants, and solvent forces; Introduction to Molecular Biophysics 27

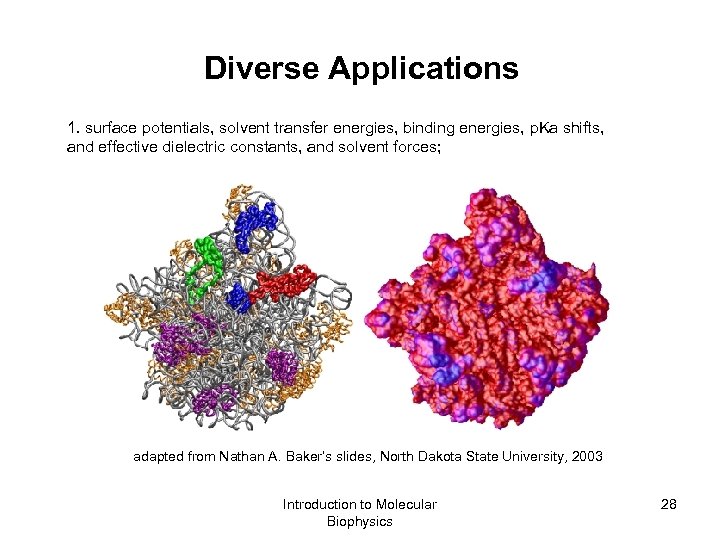Diverse Applications 1. surface potentials, solvent transfer energies, binding energies, p. Ka shifts, and effective dielectric constants, and solvent forces; adapted from Nathan A. Baker’s slides, North Dakota State University, 2003 Introduction to Molecular Biophysics 28

Diverse Applications 1. surface potentials, solvent transfer energies, binding energies, p. Ka shifts, and effective dielectric constants, and solvent forces; Determine binding energies between 30 S ribosomal subunit and aminoglycoside antibiotics - suggests importance of basic functional groups on Ring IV adapted from Nathan A. Baker’s slides, North Dakota State University, 2003 Introduction to Molecular Biophysics 29

Diverse Applications 1. solvent transfer energies, binding energies, p. Ka shifts, solvent forces, surface potentials and effective dielectric constants; 2. Protein-protein, protein-DNA, protein-ligand interactions (association, dissociation); 3. Electrostatic mediated diffusion processes (ion permeation, etc); 4. Efficient sampling of structures (not very popular yet); 5. Can apply to not only solution but also mixed system such as membrane 6. Hybrid implicit/explicit solvation models - it is possible to include a layer or sphere of water molecules around the solute, and model the bulk with an implicit solvent. Further readings: M. Feig, C. Brooks, Curr. Opin. Struct. Biol. 14, 217 (2004) T. Simonson, Rep. Prog. Phys. 66, 737 (2004) Introduction to Molecular Biophysics 33

Practical Considerations A PB model ignores the volume of ions in the medium. Therefore, PB equation is valid for dilute ionic solutions (i. e. , concentration 0. 15 M). Dielectric constant Radii (dielectric interface, importance of the boundary) Pay attention to parameterization details Ionization states of protein side chains Determining side-chain p. Kas: PDB 2 PQR is a Python software package that automates many of the common tasks of preparing structures for continuum electrostatics calculations, providing a platform-independent utility for converting protein files in PDB format to PQR format. http: //pdb 2 pqr. sourceforge. net/ H++ is an automated system that computes p. K values of ionizable groups in macromolecules and adds missing hydrogen atoms according to the specified p. H of the environment. http: //biophysics. vt. edu/H++/ Whatif http: //swift. cmbi. kun. nl/whatif/ Further readings: http: //enzyme. ucd. ie/Science/p. Ka/ D. Bashford and M. Karplus; Biochemistry, 29 10219 --10225, 1990. Introduction to Molecular Biophysics 34

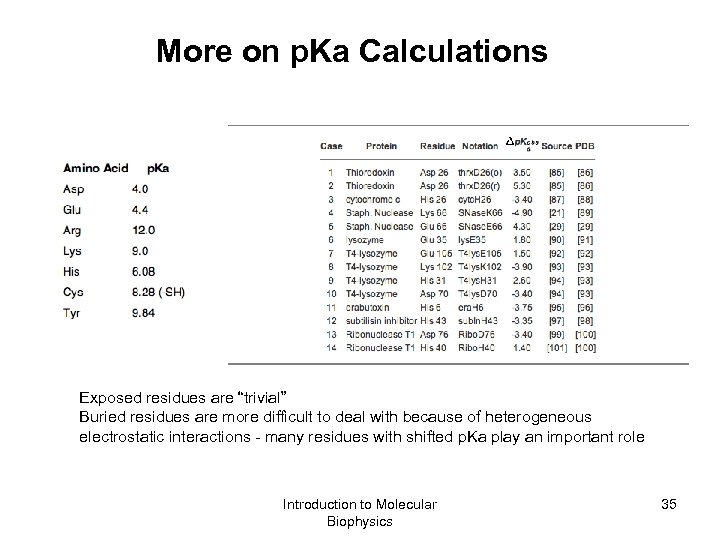More on p. Ka Calculations Exposed residues are “trivial” Buried residues are more difficult to deal with because of heterogeneous electrostatic interactions - many residues with shifted p. Ka play an important role Introduction to Molecular Biophysics 35

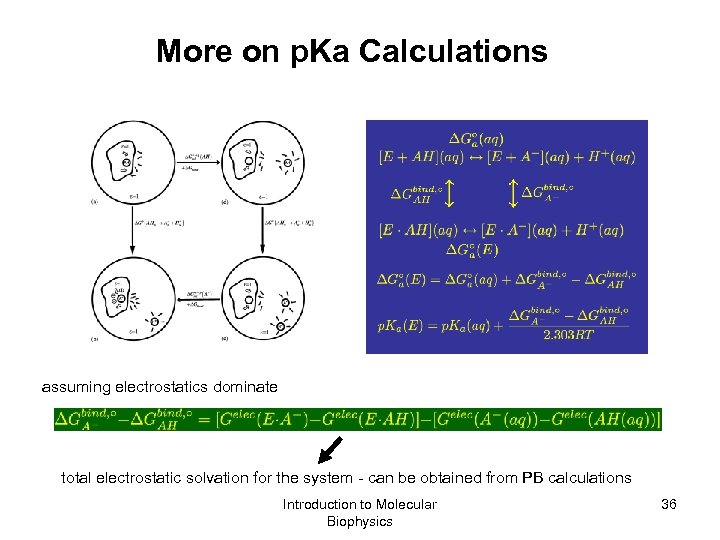More on p. Ka Calculations assuming electrostatics dominate total electrostatic solvation for the system - can be obtained from PB calculations Introduction to Molecular Biophysics 36

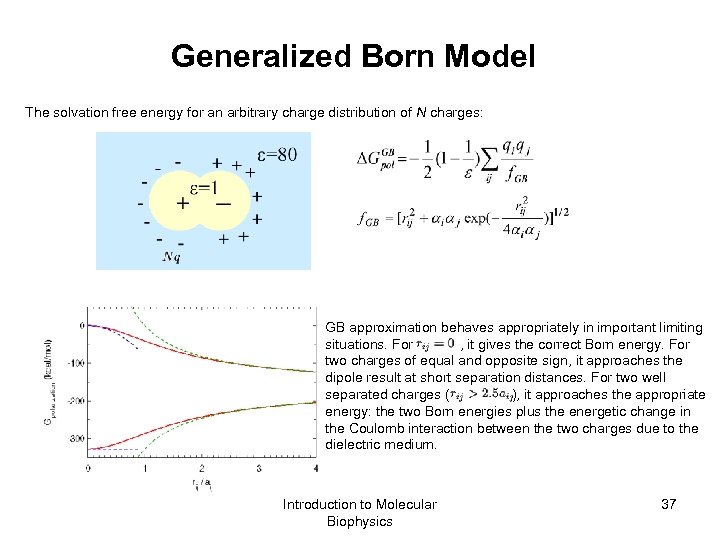Generalized Born Model The solvation free energy for an arbitrary charge distribution of N charges: GB approximation behaves appropriately in important limiting situations. For , it gives the correct Born energy. For two charges of equal and opposite sign, it approaches the dipole result at short separation distances. For two well separated charges ( ), it approaches the appropriate energy: the two Born energies plus the energetic change in the Coulomb interaction between the two charges due to the dielectric medium. Introduction to Molecular Biophysics 37

Generalized Born Model Important and Difficult: effective Born radii calculation This functional form of the so-called Generalized Born (GB) approximation has been used with considerable success to efficiently evaluate hydration energies for small molecules. Parameterization of the method involves accounting for the effects of neighboring solute atoms in the determination of each atom's effective Born radius a. Introduction to Molecular Biophysics 38

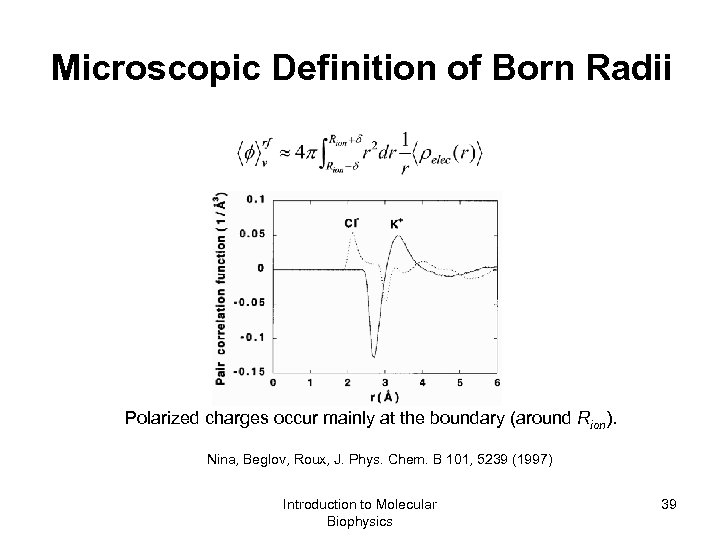Microscopic Definition of Born Radii Polarized charges occur mainly at the boundary (around Rion). Nina, Beglov, Roux, J. Phys. Chem. B 101, 5239 (1997) Introduction to Molecular Biophysics 39

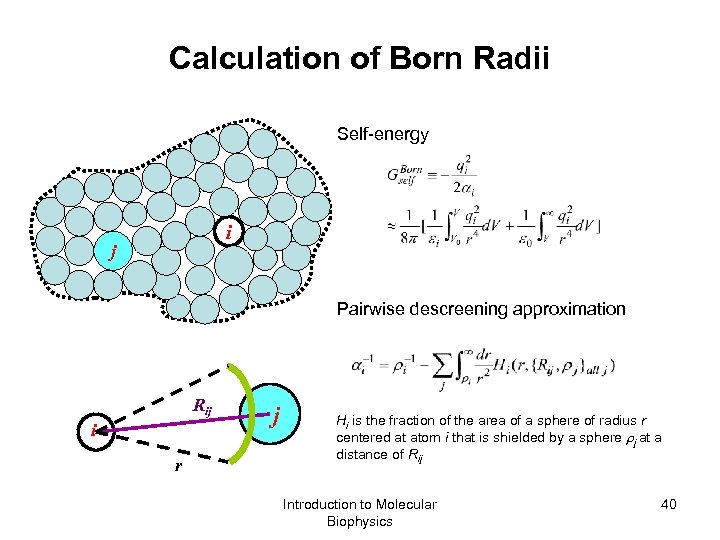Calculation of Born Radii Self-energy i j Pairwise descreening approximation Rij i r j Hi is the fraction of the area of a sphere of radius r centered at atom i that is shielded by a sphere j at a distance of Rij Introduction to Molecular Biophysics 40

Generalized Born Model A model based on further approximation to PB analytical, simple, fast and reasonable approximation Efficient sampling of structures (“dynamics” is somewhat tricky to interpret) Many successful applications: Trp-cage folding, Simmerling et al. , 2002 JACS DNA stability, Tsui et al. , 2000, JACS binding energies, MMGB/SA, P. Kollman et al. 2000, Accts. Chem. Res. constant p. H simulations J. Mongon et al. 2005, Curr. Opin. Struct. Biol. Introduction to Molecular Biophysics 41

Limitations of Implicit Solvation Models The hydrophobic effect this surface area pertains to the solute, while the hydrophobic effect is entropic in nature and occurs on the side of the solvent. Viscosity water molecules by randomly colliding and impeding the motion of solutes - makes sampling of configurations and phase space faster; misleading kinetics results; using Langevin dynamics with a damping constant Coupling between nonpolar and polar terms Recent discussion see, J. Dzubiella et al. J. Chem. Phys. 2006 Pay attention to parameterization details Over-stabilized salt-bridge Introduction to Molecular Biophysics 42

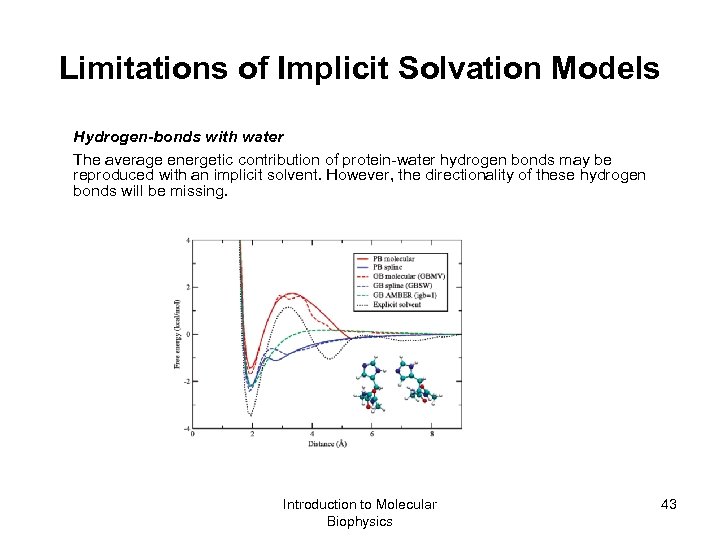Limitations of Implicit Solvation Models Hydrogen-bonds with water The average energetic contribution of protein-water hydrogen bonds may be reproduced with an implicit solvent. However, the directionality of these hydrogen bonds will be missing. Introduction to Molecular Biophysics 43