Imperfezioni dei mercati e progettazione hardware stato dell arte

Imperfezioni dei mercati e progettazione hardware: stato dell'arte delle attività` A 4. 1 -4 Enrico Scalas (DISTA Università del Piemonte Orientale) www. econophysics. org Riunione FISR Palermo - 18 -19 giugno 2004

Riassunto • Presentazione del progetto • Rassegna dei contributi recenti • Hardware in finanza I: attività proposta • Hardware in finanza II: stato di avanzamento • Conclusioni

Attività del nodo Alessandria - Genova - Canberra • A 4. 1 - Hardware nella valutazione di opzioni • A 4. 2 - Analisi della microstruttura dei mercati: opportunità di arbitraggio • A 4. 3 - Analisi della microstruttura dei mercati: altre imperfezioni • A 4. 4 - Hardware per decisioni veloci nella gestione del rischio: studio di fattibilità

Componenti del nodo Alessandria - Genova - Canberra Alessandria: Enrico Scalas (project manager) Genova: Massimo Riani (reti neuronali), Andrea Ridi (hardware) Canberra: Tiziana Di Matteo, Tomaso Aste (imperfezioni nei mercati finanziari)

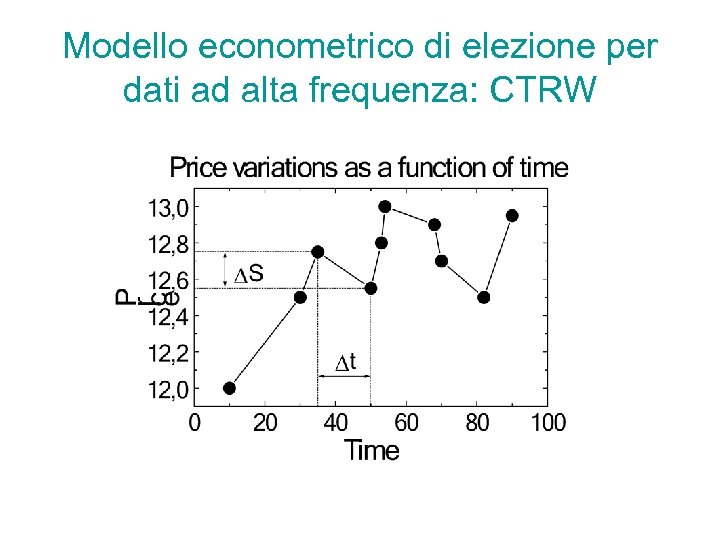Modello econometrico di elezione per dati ad alta frequenza: CTRW

Teoria (I) CTRW in finanza (quantità fondamentali) : prezzo di un bene al tempo t : log-prezzo : densità di probabilità congiunta dei salti e dei tempi di attesa : densità di probabilità di trovare il log-prezzo x al tempo t

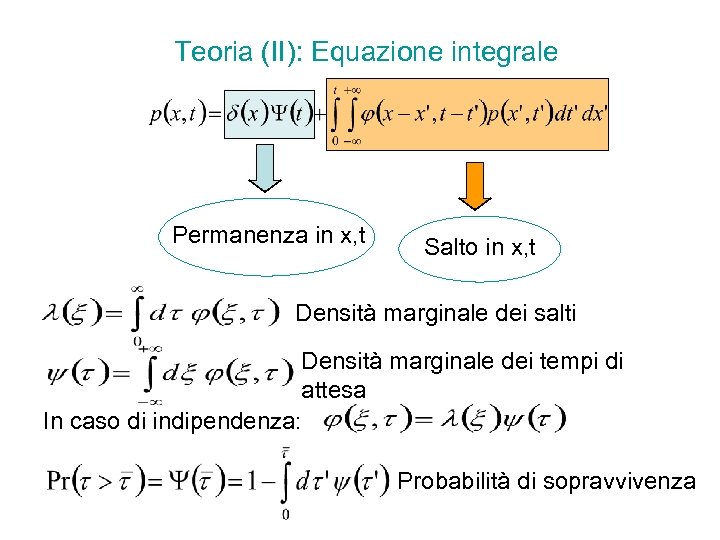Teoria (II): Equazione integrale Permanenza in x, t Salto in x, t Densità marginale dei salti Densità marginale dei tempi di attesa In caso di indipendenza: Probabilità di sopravvivenza

Esempio: il processo di Poisson composto normale (I) (S. J. Press, Journal of Business, 40, 317 -335, 1967) x(0)=0 e, se =0, x(t) è una martingala

Esempio: il processo di Poisson composto normale (II) Convoluzione di n Gaussiane La distribuzione di x è leptocurtica

Collaborazioni in corso • Densità di probabilità generali per i ritorni i tempi di attesa; (con R. Gorenflo, Berlino, Germania e F. Mainardi, Bologna, Italia, PRE, 69, 011107, 2004); • Attività variabile durante il giorno (spettro di tempi medi); (con H. Luckock, Sydney, Australia, articolo sottoposto a QF, T. Kaizoji, Tokyo, Giappone, lavoro in corso); • Dipendenza tra log-ritorni e tempi di attesa; (con M. Meerschaert, Reno, USA, in preparazione); • Mercati sintetici su supercalcolatori; (con P. Dagna, CILEA, G. Germano, Marburg, Germania e A. Vivoli, Bologna SCE 2004). • Altre forme di dipendenza (Modelli ACD (autoregressive conditional duration)); (lavoro in corso). • Legame con l’economia computazionale ad agenti; (con S. Cincotti, S. M. Focardi, L. Ponta e M. Raberto, Genova, Italia, WEHIA 2004 e SCE 2004); • Legame con l’economia sperimentale; (lavoro in corso con J. Huber e M. Kirchler, Innsbruck, Austria).

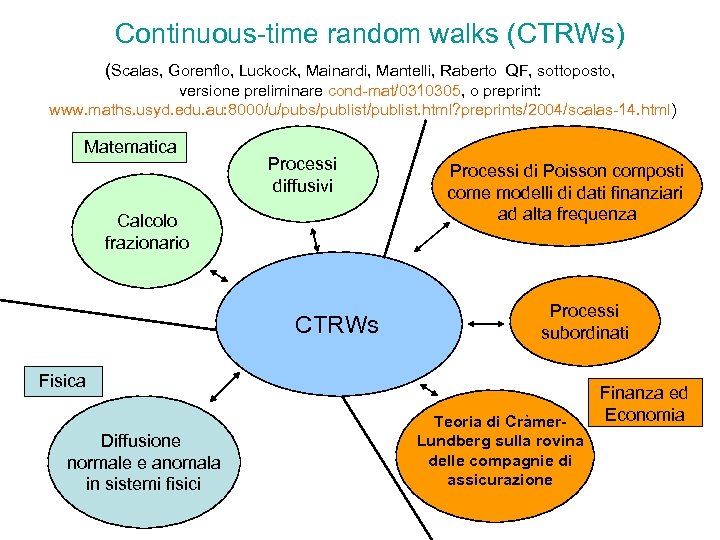Continuous-time random walks (CTRWs) (Scalas, Gorenflo, Luckock, Mainardi, Mantelli, Raberto QF, sottoposto, versione preliminare cond-mat/0310305, o preprint: www. maths. usyd. edu. au: 8000/u/pubs/publist. html? preprints/2004/scalas-14. html) Matematica Processi diffusivi Calcolo frazionario CTRWs Processi di Poisson composti come modelli di dati finanziari ad alta frequenza Processi subordinati Fisica Diffusione normale e anomala in sistemi fisici Teoria di Cràmer. Lundberg sulla rovina delle compagnie di assicurazione Finanza ed Economia

Elenco dei contributi recenti • [1] E. Scalas, R. Gorenflo, F. Mainardi, M. Mantelli, M. Raberto, Anomalous waiting times in high-frequency financial data. Vecchia versione. • [2] E. Scalas, R. Gorenflo, H. Luckock, F. Mainardi, M. Mantelli, M. Raberto, Anomalous waiting times in high-frequency financial data. Nuova versione. • [3] T. Di Matteo, M. Airoldi, E. Scalas, On pricing of interest rate derivatives. • [4] E. Scalas, Five years of continuous-time random walks in Econophysics. Invited talk presented at WEHIA 2004, Kyoto. • [5] S. Cincotti, S. M. Focardi, L. Ponta, M. Raberto, E. Scalas, The waiting-time distribution of trading activity in a double auction artificial financial market. Presented at WEHIA 2004, Kyoto. • [6] E. Scalas, S. Cincotti, S. M. Focardi, L. Ponta, M. Raberto, A double-auction artificial market with time-irregularly spaced orders. Presented at SCE 2004, Amsterdam. • [7] E. Scalas, R. Gorenflo, F. Mainardi, M. Meerschaert, Speculative option valuation and the fractional diffusion equation. Presented at FDA'04, Bordeaux.

E. Scalas, R. Gorenflo, H. Luckock, F. Mainardi, M. Mantelli, M. Raberto, Anomalous waiting times in high-frequency financial data

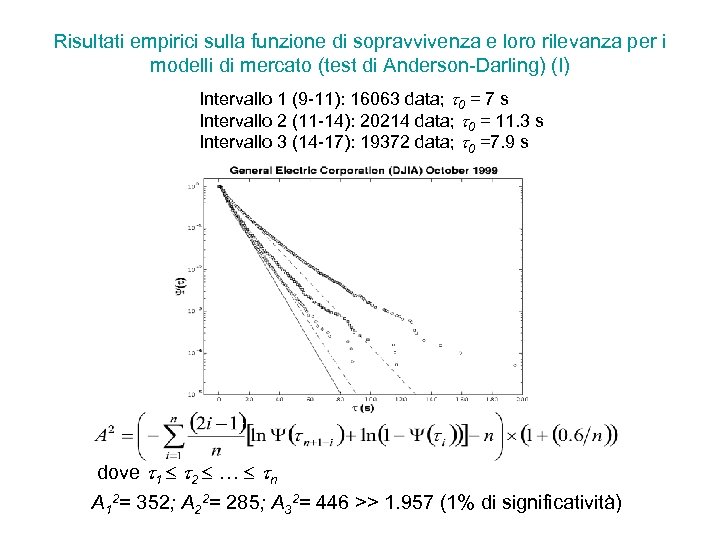Risultati empirici sulla funzione di sopravvivenza e loro rilevanza per i modelli di mercato (test di Anderson-Darling) (I) Intervallo 1 (9 -11): 16063 data; 0 = 7 s Intervallo 2 (11 -14): 20214 data; 0 = 11. 3 s Intervallo 3 (14 -17): 19372 data; 0 =7. 9 s dove 1 2 … n A 12= 352; A 22= 285; A 32= 446 >> 1. 957 (1% di significatività)

Risultati empirici sulla funzione di sopravvivenza e loro rilevanza per i modelli di mercato (II) • Funzioni di sopravvivenza non esponenziali sono state osservate da molti gruppi in vari mercati (Mainardi et al. (LIFFE), Sabatelli et al. (mercato irlandese del XIX secolo e For. Ex ), K. Kim & S. -M. Yoon (Korean Future Exchange)), si veda anche Kaizoji and Kaizoji (cond-mat/0312560) • Perché è interessante? Per la sua relazione con il meccanismo di formazione dei prezzi e con il processo degli ordini. Se il processo degli ordini fosse descrivibile mediante un processo di Poisson (funzione di sopravvivenza esponenziale), il suo campionamento casuale dovrebbe portare a un’altra distribuzione di Poisson per il processo dei prezzi. Non è così! • L’unica discussione chiara di questo punto si può trovare nei recenti lavori del gruppo che ha sviluppato il Genoa Artificial Stock Market • L’anomalia può essere spiegata in termini di attività giornaliera variabile!

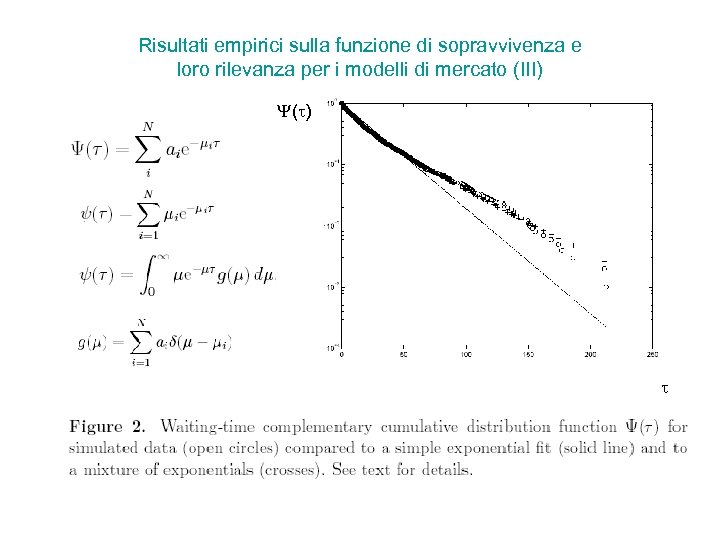Risultati empirici sulla funzione di sopravvivenza e loro rilevanza per i modelli di mercato (III) ( )

Hardware in finanza I: attività proposta (I) Si è scelto di lavorare con tecnologia Field Programmable Gate Arrays (FPGA). Vantaggi: • sono veloci (e si prestano al calcolo parallelo); • non sono particolarmente costosi; • consumano meno potenza di un PC; Problemi: • serve una formazione specifica; • ci sono linguaggi di programmazione di alto livello, ma si deve conoscere bene l’hardware per usarli.

Hardware in finanza I: attività proposta (II) Si è richiesta la fornitura di un servizio di progettazione e realizzazione di un prototipo di generatore di rumore bianco di Lévy e in generale di rumore bianco leptocurtico, da realizzarsi secondo la procedura seguente: • • definizione dell’algoritmo; realizzazione dell’algoritmo in un linguaggio evoluto, preferibilmente Matlab; validazione/ottimizzazione dell’algoritmo; traduzione dell’algoritmo in linguaggio VHDL o altro apposito linguaggio per FPGA; trasferimento del codice su FPGA; studio della simulazione hardware del rumore bianco leptocurtico; presentazione di un prototipo finale e di un rapporto dettagliato in lingua inglese sull’attività svolta.

Hardware in finanza II: stato di avanzamento • Bando (con capitolato tecnico) in scadenza il 18 giugno 2004; • Sono state invitate 5 piccole-medie aziende attive a vario titolo nel campo dell’elettronica (AETHIA, UR, Thetis, E-Magine-It, e. TT); • Si è richiesta relazione tecnica e offerta economica (tetto di 15000 euro IVA inclusa); • La commissione valutatrice si riunirà, in assenza di impedimenti, entro il CD del 25 giugno 2005.

Conclusioni • L’attività A 4. 3 è ben avviata e si è focalizzata sulle anomalie nei tempi di attesa tra ordini e tra contrattazioni. • I dati di book ad alta frequenza, appena disponibili, dovrebbero permettere di fare un salto di qualità ulteriore. • L’attività A 4. 1 ha avuto inizio con la richiesta di un servizio di progettazione e realizzazione di un prototipo di generatore di rumore leptocurtico su FPGA (prima commessa). Si prevede una seconda commessa per la realizzazione di un valutatore di opzioni su FPGA con algoritmo da discutere. • L’attività A 4. 2 sta partendo e si focalizzerà sul ruolo dell’informazione a priori (inclusa l’informazione da insider) in collaborazione con J. Huber e M. Kirchler a Innsbruck. • L’attività A 4. 4 dovrebbe partire dopo le prime esperienze di lavoro su FPGA.