Имитационное моделирование процесс конструирования модели реальной системы и

Имитационное моделирование процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить различные стратегии функционирования системы в рамках ограничений, накладываемых некоторым критерием или их совокупностью

Имитационная модель системы алгоритм, в котором определяются все наиболее существенные элементы, связи в системе и задаются начальные значения параметров, соответствующие некоторому «нулевому» моменту времени, а все последующие изменения, происходящие в системе по закону причин и следствий, вычисляются автоматически с помощью средств логической обработки данных при выполнении данного алгоритма (п/п GPSS, язык программирования BPWin)

Топологические схемы: • • простой конвейер; древовидный конвейер; конвейер с отказами; синхронизация процесса; транспортная модель; оптимизация процесса; пакетная обработка.

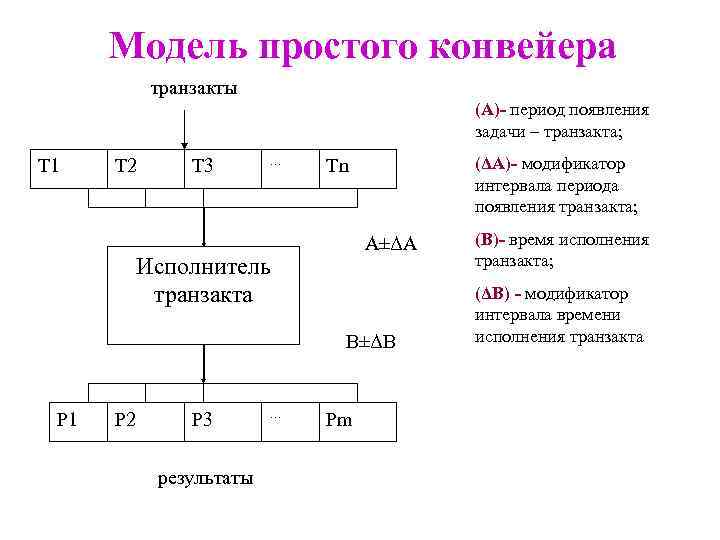Модель простого конвейера транзакты (A)- период появления задачи – транзакта; Т 1 Т 2 Т 3 … (ΔA)- модификатор интервала периода появления транзакта; Тn А±ΔА Исполнитель транзакта В±ΔВ Р 1 Р 2 Р 3 результаты … Рm (B)- время исполнения транзакта; (ΔB) - модификатор интервала времени исполнения транзакта

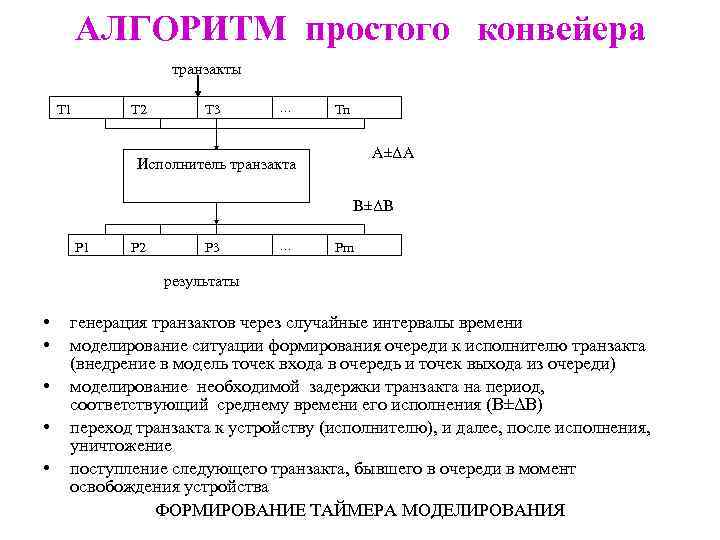АЛГОРИТМ простого конвейера транзакты Т 1 Т 2 Т 3 … Тn А±ΔА Исполнитель транзакта В±ΔВ Р 1 Р 2 Р 3 … Рm результаты • • • генерация транзактов через случайные интервалы времени моделирование ситуации формирования очереди к исполнителю транзакта (внедрение в модель точек входа в очередь и точек выхода из очереди) моделирование необходимой задержки транзакта на период, соответствующий среднему времени его исполнения (В±ΔВ) переход транзакта к устройству (исполнителю), и далее, после исполнения, уничтожение поступление следующего транзакта, бывшего в очереди в момент освобождения устройства ФОРМИРОВАНИЕ ТАЙМЕРА МОДЕЛИРОВАНИЯ

Моделирование очереди Через 20 10 За 19 5

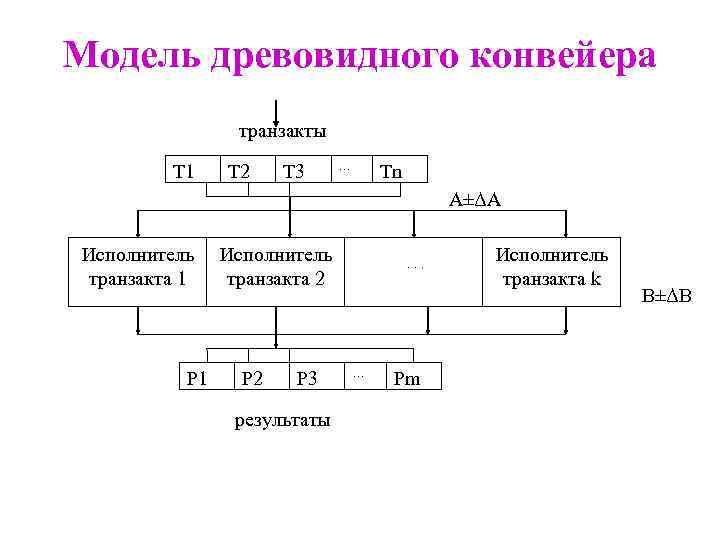Модель древовидного конвейера транзакты Т 1 Т 2 Т 3 … Тn А±ΔА Исполнитель транзакта 1 Р 1 Исполнитель транзакта 2 Р 3 результаты . . . … Рm Исполнитель транзакта k В±ΔВ

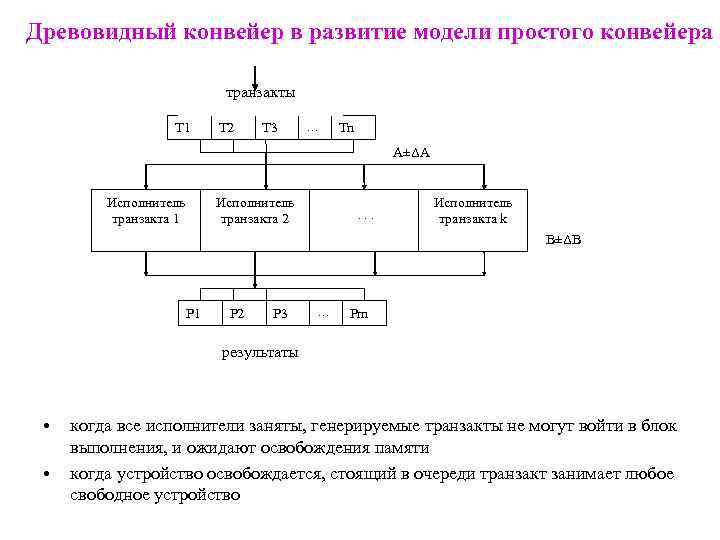Древовидный конвейер в развитие модели простого конвейера транзакты Т 1 Т 2 Т 3 … Тn А±ΔА Исполнитель транзакта 1 Исполнитель транзакта 2 . . . Исполнитель транзакта k В±ΔВ Р 1 Р 2 Р 3 … Рm результаты • • когда все исполнители заняты, генерируемые транзакты не могут войти в блок выполнения, и ожидают освобождения памяти когда устройство освобождается, стоящий в очереди транзакт занимает любое свободное устройство

Модель парикмахерской с несколькими парикмахерами 19 5 5 5

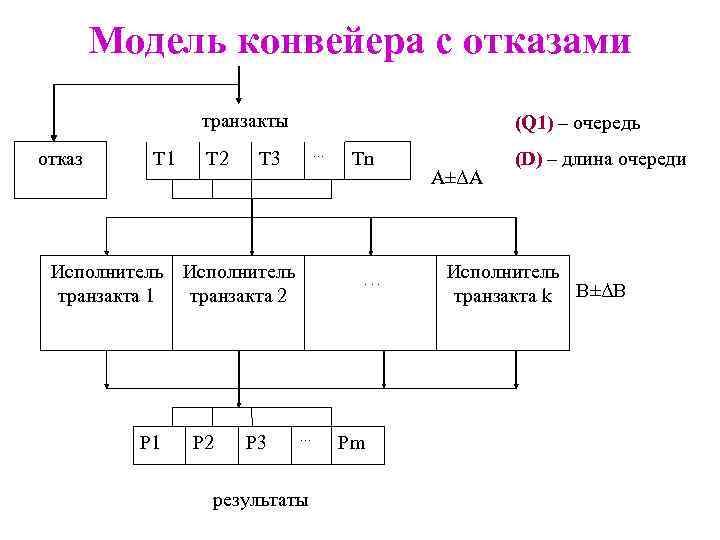Модель конвейера с отказами Q 1≤ D транзакты отказ Т 1 Исполнитель транзакта 1 Р 1 Т 2 … Т 3 Исполнитель транзакта 2 Р 3 Тn . . . … результаты Рm А±ΔА (Q 1) – очередь (D) – длина очереди Исполнитель транзакта k В±ΔВ

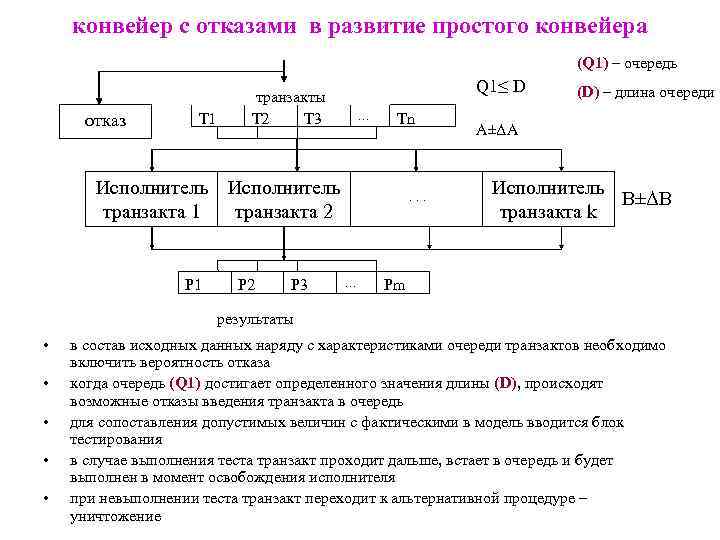конвейер с отказами в развитие простого конвейера (Q 1) – очередь отказ Т 1 Исполнитель транзакта 1 Р 1 Q 1≤ D транзакты Т 2 Т 3 … Тn Исполнитель транзакта 2 Р 3 . . . … (D) – длина очереди А±ΔА Исполнитель В±ΔВ транзакта k Рm результаты • • • в состав исходных данных наряду с характеристиками очереди транзактов необходимо включить вероятность отказа когда очередь (Q 1) достигает определенного значения длины (D), происходят возможные отказы введения транзакта в очередь для сопоставления допустимых величин с фактическими в модель вводится блок тестирования в случае выполнения теста транзакт проходит дальше, встает в очередь и будет выполнен в момент освобождения исполнителя при невыполнении теста транзакт переходит к альтернативной процедуре – уничтожение

Модель парикмахерской с несколькими парикмахерами 19 5 5 5 ОТКАЗ (если в очереди более двух)

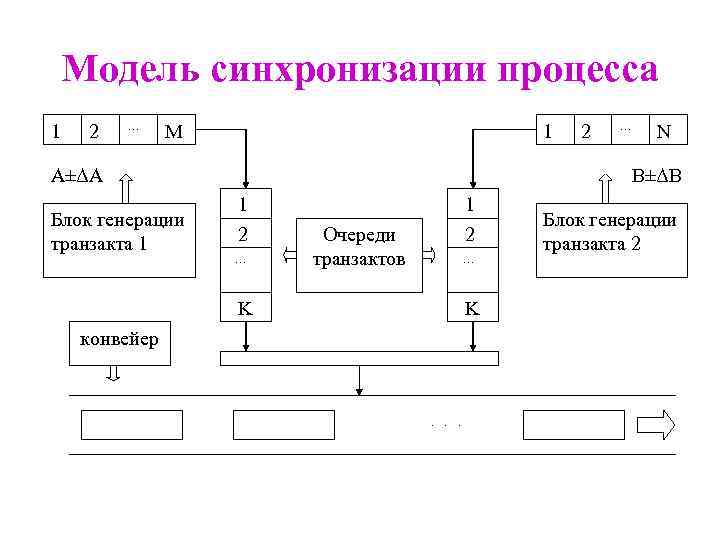Модель синхронизации процесса 1 2 … M 1 А±ΔА Блок генерации транзакта 1 2 … N В±ΔВ 1 2 … 1 2 Очереди транзактов … K K конвейер . . . Блок генерации транзакта 2

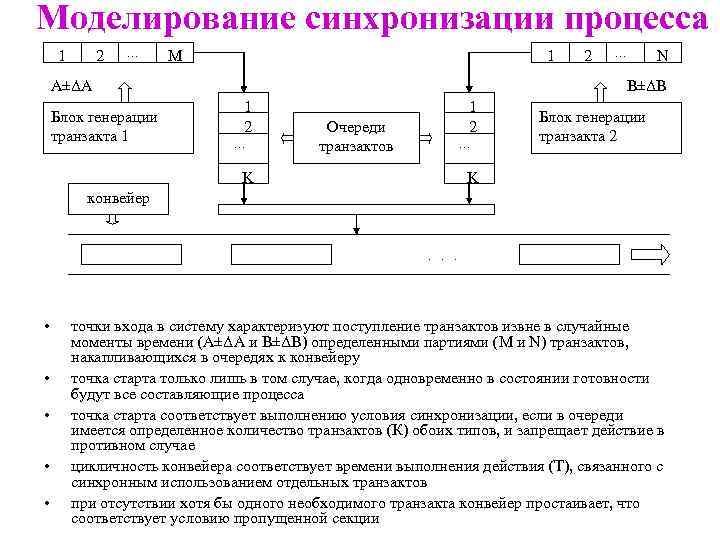Моделирование синхронизации процесса 1 2 … M 1 А±ΔА Блок генерации транзакта 1 2 … N В±ΔВ 1 2 … 1 2 Очереди транзактов … K Блок генерации транзакта 2 K конвейер . . . • • • точки входа в систему характеризуют поступление транзактов извне в случайные моменты времени (А±ΔА и В±ΔВ) определенными партиями (M и N) транзактов, накапливающихся в очередях к конвейеру точка старта только лишь в том случае, когда одновременно в состоянии готовности будут все составляющие процесса точка старта соответствует выполнению условия синхронизации, если в очереди имеется определенное количество транзактов (К) обоих типов, и запрещает действие в противном случае цикличность конвейера соответствует времени выполнения действия (Т), связанного с синхронным использованием отдельных транзактов при отсутствии хотя бы одного необходимого транзакта конвейер простаивает, что соответствует условию пропущенной секции

ПРОБЛЕМА простоя (пропуска секций) большинство пропусков секций возникает на начальном этапе в силу недостаточного запаса транзактов для синхронизации сдвиг начала работы конвейера относительно начала поступления транзактов на период, необходимый для накопления достаточного запаса транзактов запас транзактов в очередях, складывающийся в конце оперативного планируемого периода (смена), можно не расформировывать, а консервировать, сохраняя неизменным для использования в начале следующего периода

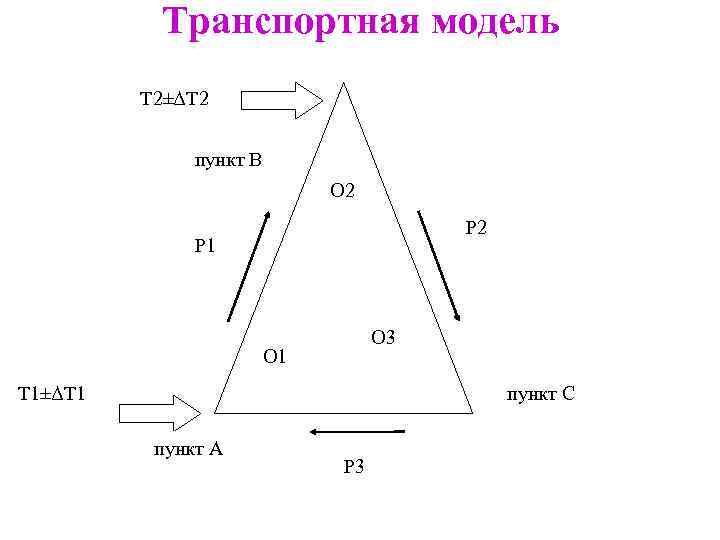Транспортная модель Т 2±ΔТ 2 пункт В O 2 P 1 O 3 O 1 Т 1±ΔТ 1 пункт С пункт А P 3

Исходные данные для транспортной модели: • количество исполнителей (N); • входные, промежуточные и целевые точки (пункты) транспортной цепи их физического или абстрактного движения (Хl); • время перемещения между ними (Рi); • время задержки на целевых или промежуточных точках (Oj); • варианты действий исполнителя при выполнении или невыполнении заданных условий в контрольных точках; • период генерации транзактов (T±ΔТ); • среднее количество генерируемых транзактов (Zk); • пропускная способность исполнителей (Fm).

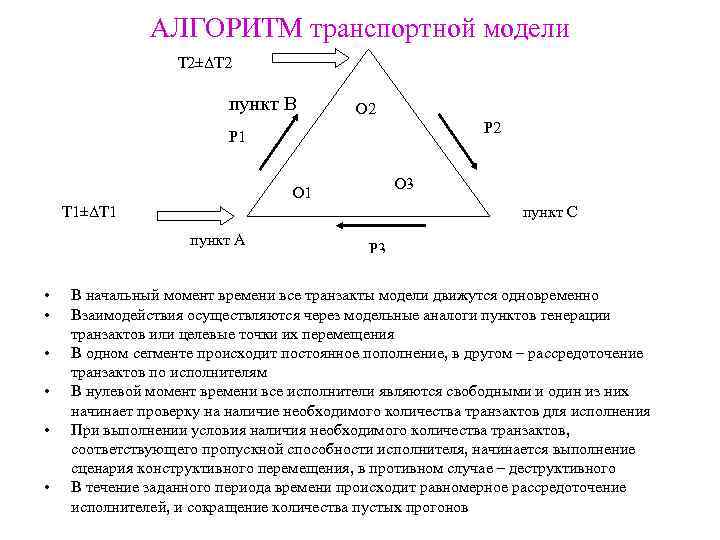АЛГОРИТМ транспортной модели Т 2±ΔТ 2 пункт В O 2 P 1 O 3 O 1 Т 1±ΔТ 1 пункт С пункт А • • • P 3 В начальный момент времени все транзакты модели движутся одновременно Взаимодействия осуществляются через модельные аналоги пунктов генерации транзактов или целевые точки их перемещения В одном сегменте происходит постоянное пополнение, в другом – рассредоточение транзактов по исполнителям В нулевой момент времени все исполнители являются свободными и один из них начинает проверку на наличие необходимого количества транзактов для исполнения При выполнении условия наличия необходимого количества транзактов, соответствующего пропускной способности исполнителя, начинается выполнение сценария конструктивного перемещения, в противном случае – деструктивного В течение заданного периода времени происходит равномерное рассредоточение исполнителей, и сокращение количества пустых прогонов

ПРОБЛЕМА простоя (пустые прогоны) 1. Нехватка транзактов 2. Остатки не перемещенных транзактов Равномерное рассредоточение исполнителей и сокращение количества пустых прогонов Включение исполнителя в процесс с задержкой, рассчитанной с учетом возможности подготовки необходимого задела транзактов для исполнения моделирование процесса без автоматического перехода всех исполнителей в начальную точку, что характеризует ситуацию «замирания» исполнителя в той точке транспортной цепи, которая соответствует концу планируемого периода и началу выполнения сценария в следующий период именно с этой точки

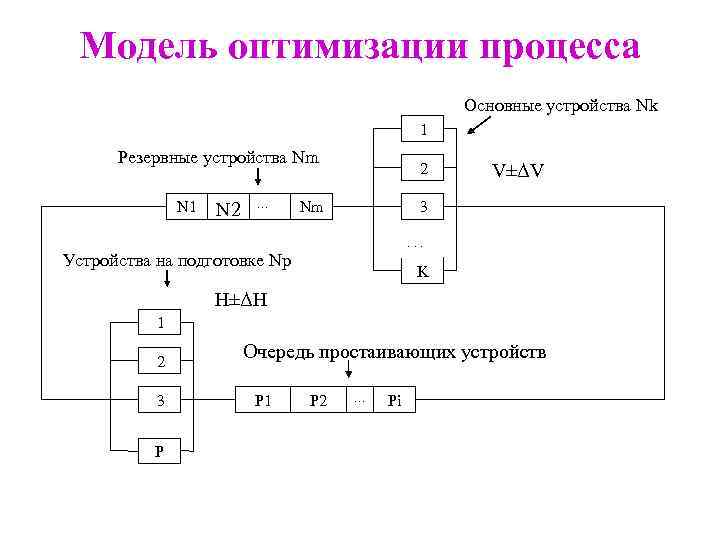Модель оптимизации процесса Основные устройства Nk 1 Резервные устройства Nm N 1 N 2 … 2 Nm V±ΔV 3. . . Устройства на подготовке Np K H±ΔH 1 2 3 P Очередь простаивающих устройств Р 1 Р 2 … Рi

Моделирование оптимизации процесса • система в целом представляет замкнутую сеть, в которой циркулируют количество заявок = основные + резервные устройства • расчет средних издержек от простоя всех устройств в течение определенного периода

COST = M * (Np + Nm) + Nk * U * C * (1 -R), где М – средние издержки на привлечение резервных устройств, Np – максимально возможное количество устройств на подготовке (напр. , оборудования в ремонте); Nm – число привлекаемых в резерв устройств; Nk – количество основных устройств; U – издержки от простоя основного устройства; С – эффективный фонд рабочего времени (напр. , продолжительность рабочего дня); R – коэффициент использования всей совокупности основных устройств, выражение (1 -R) характеризует коэффициент простоя основных устройств

Средняя интенсивность отказа основных устройств λ λ = Nk * (1/V), где Nk – общее количество основных устройств; V – среднее время безотказной работы одного основного устройства.

Интенсивность действий, связанных с простоем основных устройств μ μ должна быть не меньше чем λ, что означает ситуацию – емкость памяти в блоке «устройства на подготовке» за определенное время должна быть не меньше очереди устройств, ожидающих подготовки. μ = Np * (1/H), где Np – возможное количество мест в блоке «устройство на подготовке» ; Н – среднее время простоя устройства на подготовке.

Соотношение μ≥λ Npmin – оптимальное количество резервных устройств для минимизации издержек и обеспечения бесперебойного технологического процесса

ПРИМЕР МОДЕЛИРОВАНИЯ На трикотажной фабрике 50 швей работают на 50 машинах по 8 часов в день и по 5 дней в неделю. В случае поломки машины ее сразу заменяют резервной. Если резервных машин нет, то швея простаивает до появления резервной машины, причем почасовой убыток от простоя одной швеи составляет 20 долларов. Время ремонта 7 3 ч и возврат в цех уже в качестве резервной. Время наработки на отказ швейной машины – 157 25 ч. Оплата одного рабочего в ремонтной мастерской – 3, 75 долл/ч. Для создания запаса резервных машин предлагается кроме собственных 50 машин арендовать еще несколько по цене 30 долларов в день. Решить, сколько рабочих следует нанять для работы в мастерской и сколько машин арендовать, чтобы ежедневные издержки производства были минимальны.

Формализация задачи оптимизационная задача: COST(Nр, Nм) min, где Nр – число рабочих, нанимаемых для ремонта, Nм – число машин, арендуемых для создания резерва, COST – издержки, зависящие от выбора величин Nр и Nм.

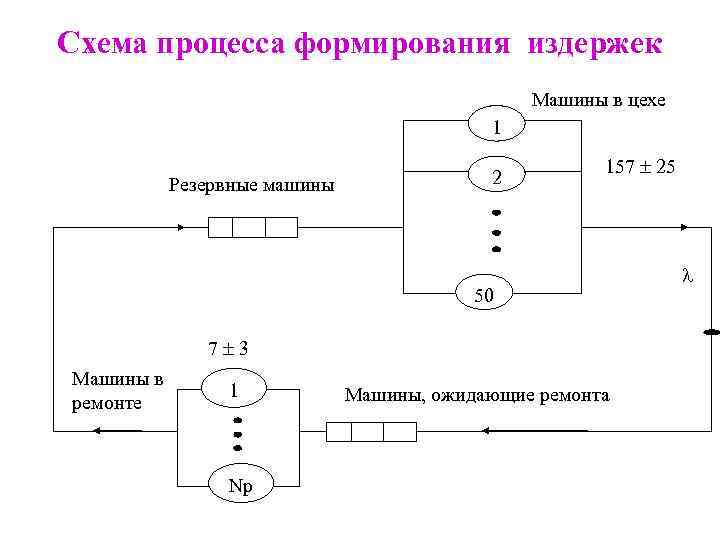Схема процесса формирования издержек Машины в цехе 1 Резервные машины 2 157 25 50 7 3 Машины в ремонте 1 Np Машины, ожидающие ремонта

Средние издержки за один рабочий день (1 -R) - коэффициент простоя – это COST = 30(Nр + Nм) + 8000(1 - R), средняя доля времени, в течение которого каждое место в цехе простаивает (швея простаивает без работы) где 30 - издержки, которые включают оплату за Nм арендуемых машин (по 30 долларов в день за одну машину) и оплату одного дня работы всем Nр рабочим, по 30 долларов в день каждому Nр – число рабочих, нанятых для работы на участке ремонта, Nм- число арендуемых для резерва машин (сверх 50 -ти собственных) R – коэффициент использования швейного цеха. 8*(1 -R) равна среднему времени простоя одной швеи в течение 8 -часового рабочего дня величина 20*8*(1 -R) – это средние издержки за рабочий день от простоя одной швеи 50*20*8*(1 -R) = 8000*(1 -R) – средние издержки за рабочий день от простоя всех 50 -ти швей

в оптимальном варианте системы R будет близок к 1 (в цехе будут практически без простоя работать все 50 швей) Тогда средняя интенсивность отказов машин составит = 50*(1/157) 1/3 (отказов в час), где - средняя интенсивность отказов всех работающих машин, т. е. среднее число машин, поступающих за 1 час на участок ремонта; 157 – среднее время между отказами одной работающей машины; 1/157 – средняя интенсивность отказов одной машины; 50 – число работающих машин в цехе

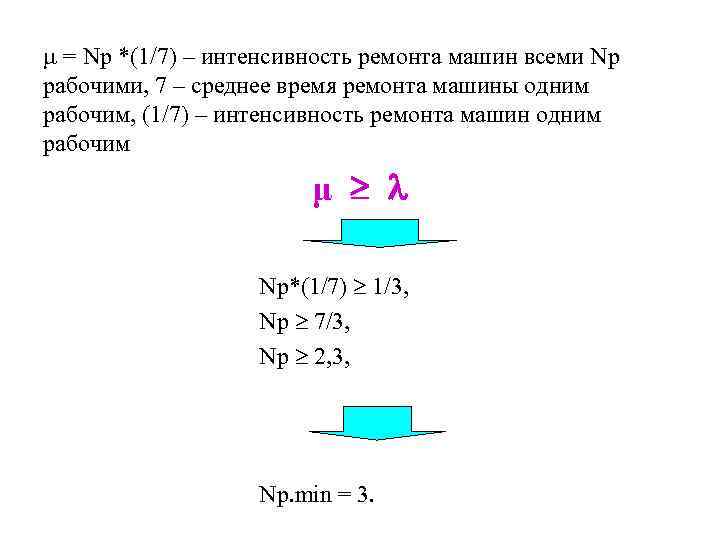= Nр *(1/7) – интенсивность ремонта машин всеми Nр рабочими, 7 – среднее время ремонта машины одним рабочим, (1/7) – интенсивность ремонта машин одним рабочим μ Nр*(1/7) 1/3, Nр 7/3, Nр 2, 3, Nр. min = 3.

в оптимальном решении Nр 3, можно предположить, что и число резервных машин Nм также должно быть не меньше трех, т. к. для того, чтобы 50 машин работало, а 3 находились в ремонте, нужно иметь три резервных машины.

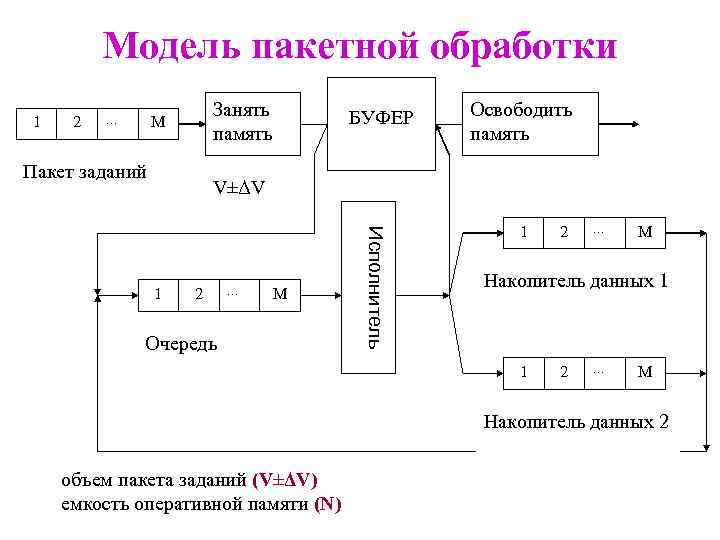Модель пакетной обработки 1 2 … Занять память M Пакет заданий БУФЕР Освободить память V±ΔV 2 … M Очередь Исполнитель 1 1 2 … M Накопитель данных 2 объем пакета заданий (V±ΔV) емкость оперативной памяти (N)

Моделирование пакетной обработки • Если транзакт может быть загружен в оперативную память, то он фиксируется в блоке занятия памяти и поступает в очередь к исполнителю • транзакт исполняется и со случайной вероятностью может обращаться к накопителям или завершаться (моделирование сценариев) • ЛИНИЯ ОБРАТНОЙ СВЯЗИ - прохождение транзакта после исполнения в накопители данных, систематизирующих информацию по различным критериям, и возвращающих транзакты обратно в очередь к исполнителю в случае неадекватности планируемых и фактических параметров • ВЫХОД ИЗ КОНТУРА - при условии адекватности выработанного решения определенным критериям завершение транзакта и возврат в буфер, т. к. в процессе корректировки решения по управленческому контуру более нет необходимости