TMO_0_веч_2012.ppt
- Количество слайдов: 197

Имитационное моделирование экономических процессов. Теория массового обслуживания

Имитационное моделирование экономических процессов Основные понятия Литература • 1. Емельянов А. А. , Власова Е. А. , Дума Р. В. , Емельянова Н. З. Компьютерная имитация экономических процессов. Монография. – М. : МФПА, 2010. – 464 с. • 2. Н. Н. Прокимнов. Моделирование систем (сайт МФПА). – М. : МФПА, 2007.

Введение • «Даже если ваше объяснение настолько • ясно, что исключает всякое ложное толкование, все равно найдется человек, который поймет вас неправильно» • Основы теории массового обслуживания были заложены трудами известного датского ученого А. Эрланга (1878 -1929). Задачи теории возникают в самых разнообразных направлениях: в естествознании, в экономике, в технике и т. д. Логика, лежащая в основе функционирования систем, может быть сведена к обобщенному набору простых операций.

Введение • Тем самым создаютс условия для имитационного (simulation) моделирования, реализуемого, в общем случае, с помощью соответствующего набора математических средств (и компьютерных программ). Моделирование – сложнейший многоэтапный процесс исследования систем, направленный на выявление свойств и закономерностей, присущих исследуемым системам, с целью их создания или модернизации и эксплуатации.

Введение • Помня теорему, что «всякое уравнение длиной более двух сантиметров, скорее всего, неверно» , будем стремиться при изложении использовать сравнительно простые математические зависимости. • В теории массового обслуживания особую роль играют случайные процессы (в частности, процессы Маркова), включая различные обобщения. Однако их теория слишком сложна. На практике удобно оперировать более простыми объектами.

Введение • Например, нагрузка- показатель степени загруженности сервера: =(приведенная интенсивность поступления транзактов)/(приведенная интенсивность обслуживания). Основной входной характеристикой потока заявок является его интенсивность – среднее число заявок, проходящих за единицу времени. Вы знаете, что в простейшем потоке транзакты на входе распределены по экспоненциальному закону с функцией распределения

Введение • Величина, обратная средней длительности (ts)обслуживания, характеризует среднее число заявок, которое может быть обслужено за единицу времени, и называется интенсивностью обслуживания- .

• Производительность системы, представляет собой интенсивность с потока обслуженных заявок, выходящих из системы: с = , • где - вероятность того, что поступившая в систему заявка будет обслужена. В нашем случае (без потерь) вероятность =1. • Вводится также коэффициент загрузки или просто загрузка системы, определяемая как доля времени, в течение которого система (в случае одноканальной СМО – сервер) работает.

Сумма n стационарных ординарных потоков с интенсивностями i образует простейший поток с суммарной интенсивностью. Этот поток будет близок к простейшему при значении n>5. • Верно утверждение, что при суммировании независимых простейших потоков суммарный поток будет простейшим при любом значении n. Простейшие потоки позволяют легко получить в явном виде зависимости характеристик от параметров. Совет: не проводить имитационное моделирование, если можно решить задачу аналитически.

Введение Другие характеристики СМО для однородных потоков: • - среднее время пребывания заявок в системе складывается из времени ожидания и времени обслуживания. В этом случае среднее число транзактов в системе (в очереди и на обслуживании в • сервере) равно произведению среднего времени пребывания заявок в системе на производительность системы, т. е. интенсивность потока обслуженных заявок, выходящих из системы т= с(tw+ts).

• Эти соотношения для однородных потоков известны как формулы Литтла и вместе с соотношением для длины очереди заявок (L= с t w) представляют собой фундаментальные зависимости, справедливые для широкого класса моделей массового обслуживания. Можно также сделать вывод, что нагрузка (интенсивность входного потока, умноженная на среднее время обслуживания) характеризует среднее число заявок, находящихся на обслуживании.

Введение Если длительность обслуживания заявок предполагается распределенной по экспоненциальному закону, то это существенно упрощает аналитические выкладки. Объясняется это тем, что процессы, протекающие в системах с экспоненциальным распределением интервалов времени, являются марковскими. • Стратегия управления потоками заявок в моделях массового обслуживания задается в виде:

Введение - дисциплины буферизации (ДБ); - дисциплины обслуживания (ДО). Они могут быть классифицированы по следующим признакам: наличие приоритета, характера вытеснение заявок из очереди, возможности изменения приоритета в процессе моделирования и т. д. • Часто ёмкость накопителя в моделях предполагается неограниченной, несмотря на то, что в реальной системе соответствующая ёмкость ограничена. Такое предположение оправдано в тех

Введение случаях, когда вероятность потери заявки в реальной системе из-за переполнения ограниченной ёмкости накопителя меньше 10 -3, поскольку в этом случае дисциплина буферизации практически не влияет на характеристики обслуживания заявок. • По количеству обслуживающих серверов СМО делятся на: • одноканальные содержащие 1 сервер; • многоканальные.

Введение Такое предположение оправдано в тех случаях, когда вероятность потери заявки в реальной системе из-за переполнения ограниченной ёмкости накопителя меньше 10 -3, поскольку в этом случае дисциплина буферизации практически не влияет на характеристики обслуживания заявок. • По количеству классов транзактов поступающих в СМО различают: • с однородным потоком; • с неоднородным.
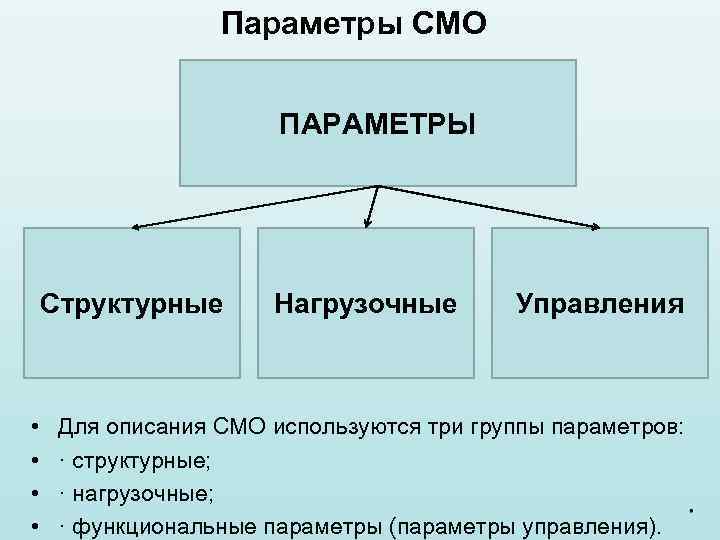
Параметры СМО ПАРАМЕТРЫ Структурные • • Нагрузочные Управления Для описания СМО используются три группы параметров: · структурные; · нагрузочные; · функциональные параметры (параметры управления).

Вероятностное разрежение потока • Вероятностное разрежение простейшего потока заявок, при котором любая заявка случайным образом с некоторой вероятностью p исключается из потока независимо от того, исключены другие заявки или нет, приводит к образованию простейшего потока с интенсивностью • ' = p , • где – интенсивность исходного потока. Поток исключенных заявок – тоже простейший с интенсивностью

Вероятностное разрежение потока • '' =(1 - p) . • Длительность обслуживания – время нахождения заявки в сервере – • в общем случае является величиной случайной и описывается некоторой плотностью распределения. В случае неоднородной нагрузки длительности обслуживания заявок разных классов могут различаться законами распределений или только средними значениями. При этом обычно предполагается независимость

Аналитические выкладки длительностей обслуживания заявок каждого класса. • В том случае, когда длительность обслуживания заявок предполагается распределенной по экспоненциальному закону справедливы известные формулы и соответствующие аналитические выкладки (случай марковских потоков).

Аналитические выкладки • Во многих случаях аналитические зависимости могут быть получены для произвольного закона распределения длительности обслуживания заявок. При этом для определения средних значений характеристик обслуживания, зачастую, как будет показано ниже, достаточно задать, кроме математического ожидания ts, второй момент распределения • (дисперсию) или коэффициент вариации длительности обслуживания.

Аналитические выкладки Заметим, что в простейшем случае, при наличии исключенных заявок, поток исключенных заявок – тоже простейший с интенсивностью = (1 - ). Обычно исследование систем проводится в предположении о стационарности входящего потока заявок и длительности обслуживания. В этом случае условие существования установившегося режима для СМО с накопителем неограниченной ёмкости совпадает с

Аналитические выкладки условием отсутствия перегрузок в СМО и записывается в виде: <1. При отсутствии перегрузок нагрузка и загрузка совпадают. Загрузку можно представлять как вероятность того, что сервер работает).

Сеть • Сеть массового обслуживания (Се. МО) – совокупность взаимосвязанных СМО, в среде которых циркулируют заявки. • Основными элементами Се. МО являются узлы (У) и источники заявок (И). • Узел сети представляет собой систему массового обслуживания. • Источник – генератор заявок, поступающих в сеть и требующих • определенных этапов обслуживания в узлах сети.

Сеть • Для упрощенного изображения Се. МО используется граф Се. МО. • Граф Се. МО – ориентированный граф, вершины которого соответствуют узлам Се. МО, а дуги отображают переходы заявок между узлами. • Переходы заявок между узлами Се. МО, в общем случае, могут быть заданы в виде вероятностей передач. • Путь движения заявок в Се. МО называется маршрутом.

Характеристики СМО с неоднородным потоком заявок • Кратко коснемся характеристик СМО с неоднородным потоком заявок. • Для СМО с неоднородным потоком заявок, в которую поступают H классов заявок с интенсивностями 1, …, 1 Н и средними длительностями обслуживания ts, определяются две группы характеристик обслуживания заявок: • характеристики по каждому классу (потоку) заявок; • характеристики объединённого

Характеристики СМО с неоднородным потоком заявок (суммарного) потока заявок. • Характеристики по каждому классу заявок идентичны вышерассмотренным характеристикам СМО с однородным потоком. • Характеристики объединённого (суммарного) потока заявок позволяют определить усредненные по всем классам заявок показатели эффективности функционирования СМО: • -суммарная интенсивность поступления

Характеристики СМО с неоднородным потоком заявок в систему (интенсивность суммарного потока): • - суммарная нагрузка • и т. д. • Можно доказать, что для характеристик объединённого (суммарного) потока справедливы те же фундаментальные соотношения, что и для однородного потока, о которых говорилось выше.

Параметры и характеристики Се. МО • Для описания линейных разомкнутых и замкнутых однородных экспоненциальных Се. МО используется следующая совокупность параметров: • - число узлов в сети: n; • - число обслуживающих приборов в узлах сети; • - матрица вероятностей передач: P = [ pij i, j = 0, 1, …, n] , где pij – вероятность передачи заявки из узла i в узел j; • - интенсивность 0 источника заявок,

Параметры и характеристики Се. МО поступающих в разомкнутую Се. МО (РСе. МО), или число заявок M, циркулирующих в замкнутой Се. МО (ЗСе. МО); • - средние длительности обслуживания заявок в узлах сети. • Заметим, что состав параметров разомкнутых и замкнутых Се. МО различается только одним параметром, а именно: для ЗСе. МО, в отличие от • РСе. МО, вместо интенсивности 0 поступления заявок в сеть необходимо

Параметры и характеристики Се. МО задать число постоянно циркулирующих в сети заявок M.

структурами данных. Альтернативой этому является использование специализированных языков. • Специализированные языки имеют свои средства описания структуры и процесса функционирования моделируемой системы, что значительно облегчает и упрощает программирование имитационных моделей. Несмотря на появление в последнее время различных моделирующих пакетов прикладных программ, в курсе учтены тенденции применения их в экономических науках. Среди наиболее популярных

по –прежнему остаются два направления, схожих по своим принципам. Одним из них является достаточно эффективный и распространенный язык моделирования сложных дискретных систем - GPSS, созданный Джеффри Гордоном более 40 лет назад. Вторым является популярная методология – Pilgrim, созданная заведующим нашей кафедрой профессором А. А. Емельяновым (более 20 лет назад). Итак, современные версии GPSS и Pilgrim занимают достойное место в науке и образовании. Прежде чем приступить к их изучению, кратко рассмотрим само имитационное моделирование.

Введение. Имитационное моделирование • Имитационное моделирование играет важную роль для оценки погрешностей результатов, полученных приближенными аналитическими методами. Например, при исследовании вычислительных систем и сетей разных классов в качестве моделей функционирования широко применяются упоминавшиеся системы (СМО) и сети массового обслуживания (Се. МО). В общем случае расчет Се. МО выполняется на основе декомпозиции сети и сводится к расчету взаимосвязанных СМО типа G/G/1

Введение. Имитационное моделирование (в символике Кендалла), характеризующихся сложным (произвольным) распределением промежутков времени между моментами поступления заявок и произвольным распределением времени обслуживания. Для таких СМО отсутствуют точные аналитические методы расчета характеристик обслуживания заявок, что не позволяет детально изучить свойства и закономерности, присущие протекающим в них процессам, а следовательно, построить приемлемые для инженерных целей

Имитационное моделирование методы расчета Се. МО. Как показывают исследования, среди приближенных методов расчета СМО (типа G/G/1) наиболее эффективны формулы для оценки среднего времени ожидания заявок и коэффициента вариации исходящего потока заявок (транзактов). В связи с этим представляет интерес задача исследования характеристик обслуживания заявок и коэффициента вариации исходящего потока в СМО типа G/G/1 при различных законах распределений транзактов и времени обслуживания в ОА

GPSS World а также оценка погрешностей, возникающих при использовании упомянутых приближенных формул. Для решения поставленной задачи проводятся эксперименты на имитационных моделях в среде GPSS World (!). Как уже говорилось, макроязык GPSS для моделирования дискретных систем с его разновидностями (GPSS World) является долгожителем среди множества языков, предназначенных для имитационного моделирования сложных систем.

GPSS World Конец прошлого века ознаменовался разработкой компанией Minuteman Software программного продукта GPSS World, увидевшей свет в 1993 году. За сравнительно небольшой период времени было выпущено несколько его версий, причем в каждой последующей возможности системы моделирования наращивались. Нам необходимо ознакомится с общим подходом к программированию на GPSS World. Как каждый язык, GPSS World имеет свой строго используемый алфавит.

Алфавит GPSS World • В алфавит языка GPSS входят следующие символы: • A, B, . . . , Z - большие буквы латинского алфавита, • 1, 2, . . , 9, 0 - цифры, • ? – вопросительный знак (для вызова помощи), • ( - левая скобка, • ) - правая скобка, • ‘ - апостроф, • . – точка,

• знаки арифметических действий (# - умножение, / - деление), • , - запятая, • - пробел. • Формальные правила написания программ на языке GPSS образуют его синтаксис (греч. σύνταξις — «построение, порядок» ). • В GPSS имеется текстовые объекты. • При моделировании между системой, описываемой на языке GPSS (GPSSсистемой), и моделируемой реальной системой устанавливают определенное логическое соответствие, которое

GPSS World позволяет из сведений, получаемых при анализе GPSS-системы, делать определенные выводы о реальной системе. Такие выводы называют интерпретацией GPSS-систем. Правила интерпретации GPSS-систем составляют семантику языка GPSS (греч. σημαντικός — обозначающий). Наряду с синтаксическим и семантическим аспектами языка большое значение имеет его прагматический аспект. Прагматика языка включает сведения по его практическому использованию, в том

числе типичные приемы написания программ на этом языке, методы организации их отладки и выполнения и т. д. Они познаются на практике. Очень важен анализ полученных результатов. Объекты GPSS можно подразделить на 7 категорий и 15 типов. Семь классов представляют собой: динамические, операционные, аппаратные, статистические, вычислительные, запоминающие и группирующие. Все объекты имеют собственные окна.

Динамические объекты, представляющие элементы потока обслуживания, называются, как говорилось, транзактами. Содержательное значение их определяет разработчик(!). С каждым транзактом может быть связано произвольное число параметров, несущих в себе необходимую информацию об нем. Кроме того, транзакты могут иметь различные приоритеты. Основа GPSS – программы, описывающие функционирование объектов, и специальная программа – диспетчер. Приведем классы и их объекты:
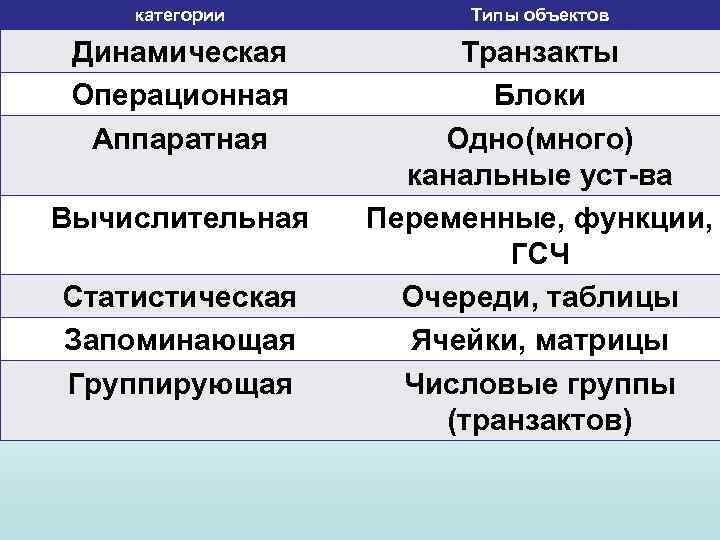
категории Типы объектов Динамическая Операционная Аппаратная Транзакты Блоки Одно(много) канальные уст-ва Переменные, функции, ГСЧ Очереди, таблицы Ячейки, матрицы Числовые группы (транзактов) Вычислительная Статистическая Запоминающая Группирующая

Динамические объекты GPSS World Итак, динамические объекты – транзакты. Работа GPSS-модели заключается в «перемещении» транзактов от блока к блоку. Они создаются или уничтожаются в соответствии с логикой модели. С каждым транзактом м. б. связано некоторое число параметров- системных числовых атрибутов (СЧА). Далее рассмотрим применение GPSS.

Применение GPSS World • Например, GPSS может применяться для исследований полевых процессов уборки зерновых культур. Предварительными лабораторными и полевыми исследованиями следует установить основные зависимости соответствующих параметров от некоторых факторов. Например, определить влияние влажности компонентов убираемого материала на производительность загрузочного аппарата, уровень потерь и вымолот зерна при различных подачах.

Применение GPSS World Установить характеристики процессов движения агрегатов и замены технологических емкостей, а также законы варьирования размеров полей и расстояний перевозок. Закономерности изменения состояния компонентов урожая в поле в зависимости от погодных условий можно взять из литературы. • Поскольку объектом исследования является вновь разрабатываемый процесс, а задачей исследования - определение параметров технических

средств, то перед исследователями встает необходимость более детального описания этого процесса. Требуется разработать модель работы уборочных агрегатов в поле, разыгрывающая все возможные прерывания, происходящие по причинам поломок, забиваний, обмена технологическими емкостями, плохой погоды, распутицы и т. д. В результате получается некоторая область оптимальных параметров технических средств, обеспечивающих более высокую эффективность технологии уборки урожая.

GPSS World может применяться для исследования беспроводных сетей передачи данных, что является достаточно актуальным направлением развития сетевой индустрии. Беспроводная технология позволяет в кратчайшие сроки и с небольшими затратами объединить удаленные локальные сети различных организаций в единую региональную сеть передачи данных, обеспечивая им удаленный высокоскоростной стационарный доступ в Интернет. Основной структурной единицей региональной беспроводной сети является радиосота. GPSS применяется

Имитационное моделирование GPSS World для имитационного моделирования типовой радиосоты. Радиосота объединяет некоторое количество оконечных станций, каждая из которых подключает к ней локальную кабельную сеть типа Ethernet, состоящую из множества терминалов и одного или нескольких серверов. При моделировании реализуется т. н. метод CSMA/CA (множественный доступ с прослушиванием несущей и исключением коллизий).

Имитационное моделирование GPSS World Согласно этому методу последовательные попытки передачи каждой станции беспроводной сети отделены друг от друга некоторым интервалом времени задержки, а также случайным отложенным временем. Станция, успешно принявшая фрейм DATA, содержащий информационный пакет, немедленно отвечает положительным подтверждением ACK и т. д. Результатом имитационного моделирования радиосоты сети служит оценка таких показателей

GPSS World производительности, как пропускные способности, обеспечиваемые для клиентов локальных сетей, подключенных к радиосоте, средние значения времени, требуемого для успешной передачи одного пакета и т. д. Таким образом устанавливается связь или аналогия между транзактами модели и реальными элементами системы. Для облегчения пользователю моделирования в GPSS разработан язык блок-схем, но обычно фигур образуется слишком много,

что затрудняет их рассмотрение. Операционные объекты – блоки, которые задают логику функционирования системы. В блоках могут происходить события четырех типов: 1) Создание/уничтожение транзактов (могут сразу уничтожаться несколько транзактов); 2) Изменение числового атрибута объекта; 3) Задержка транзакта на определенный период времени в ОА или сервере;

GPSS World 4) Изменение маршрута движения транзакта в соответствии с логикой работы системы. Объекты аппаратной категории соответствуют элементам оборудования, которые управляются транзактами. К статистическим объектам относятся очереди и таблицы и т. д. Формат блока имеет общий вид [<метка>] <Операция> <Операнды>[<Комментарии>] Рассматриваемая версия GPSS World содержит около 50 типов блоков.

GPSS World Рассмотрим более точно предназначение этих блоков (в зависимости от принадлежности к группе): 1) Блоки, осуществляющие модификацию атрибутов: а) генерирование и уничтожение транзактов GENERATE, TERMINATE, SPLIT и др. ; б) осуществление временной задержки ADVANCE; в) синхронизация MATC двух транзактов (GATHER); г) изменение параметров транзактов ASSIGN, INDEX, MARK, PLUS; д) изменение приоритета PRIORITY.

Операционные объекты GPSS World 2) Блоки, изменяющие последовательность движения транзактов (блоки передачи управления): DISPLACE, TRANSFER, LOOP, TEST 3) Блоки, связанные с группирующей категорией: ADOPT, ALTER, EXAMINE, JOIN, REMOVE, SCAN. 4) Блоки, описывающие объекты аппаратной категории: а) одноканальные устройства SEIZE, RELEASE, PREEMPT, RETURN, FUNAVAIL и др. ; б) многоканальные устройства (памяти) ENTER, LEAVE, SAVAIL, SUNAVAIL; в) ключи (логические переключатели) LOGIC.

GPSS World 5) Блоки, сохраняющие необходимые значения SAVEVALUE, MSAVEVALUE. 6) Блоки, обеспечивающие получение статистических результатов: а) очереди QUEUE, DEPART; б) таблицы TABULATE. 7) Блоки для организации списка пользователя: LINK, UNLINK. 8) Блоки для организации ввода/вывода OPEN/CLOSE, READ/WRITE, SEEK. 9) Специальные блоки BUFFER, COUNT, EXECUTE, INTEGRATION, SELECT, TRACE, UNTRACE.

GPSS World Команды GPSS World в соответствии со своим назначением делятся на две группы: - Команды определения объектов GPSS; - Команды управления процессом моделирования. Операторы-команды позволяют управлять работой интегрированной среды GPSS. После трансляции исходной программы в памяти создается так называемая текущая модель, являющаяся совокупностью разного типа объектов, каждый из которых представляет собой некоторый набор чисел в памяти, описывающих свойства и текущее состояние объекта.

Блоки формируют логику модели, давая транзактам указания: куда идти и что делать дальше. Логические переключатели (ЛП) используются для моделирования двоичных состояний логического или физического характера. ЛП может находиться в двух состояниях: включено и выключено. Его состояние может изменяться в процессе моделирования, а также опрашиваться. Статистические объекты собирают и обрабатывают информацию. Каждая очередь обеспечивает сбор и обработку данных о транзактах, задержанных в какой-либо точке модели. Таблицы используются для получения выборочных распределений некоторых случайных величин.

GPSS World Запустить систему GPSS World можно обычным способом и появится главное окно. В верхней части располагается строка заголовка. Ниже находится основное меню. Еще ниже – панель инструментов, за которой расположена клиентская область. В самой нижней части размещена строка состояния. Для вводе текста имеется текстовый редактор. Выберем в меню File пункт New (появится окно Новый документ и выберем Модель) и откроем окно редактора, где набираем текст моделей. Начинаем так:

Программа GPSS World GENERATE (EXPONENTIONAL (1, 0, 12)) SEIZE T ADVANCE (EXPONENTIONAL (1, 0, 10)) RELEASE T TERMINATE 1 START 100 Текст можно набирать, используя выбор Edit→ Insert GPSS Blocks… Сохраним файл, создав для него папку. Для запуска необходимо набрать Command → Create Simulation, затем Command →Start.

Программа GPSS World Блок GENERATE (EXPONENTIONAL (1, 0, 12)) осуществляет ввод транзактов в модель. Для этого конкретного блока время поступления случайно и распределено по экспоненциальному закону со средним временем, равным 12 единиц. Блок SEIZE T служит целям установления факта использования устройства входящим в него транзактом. Имя устройства Т. Блок ADVANCE (EXPONENTIONAL (1, 0, 10)) задерживает продвижение транзакта, т. е. «обслуживает» его. В нем может находиться любое множество транзактов.

Программа GPSS World Время обслуживания также распределено по экспоненциальному закону со средним временем 10 единиц. Блок RELEASE T освобождает канал Т. Блок TERMINATE 1 удаляет транзакты (по одному). START 100 означает, что пройдет 100 транзактов. Напоминаем, что текст можно набирать, используя выбор Edit→ Insert GPSS Blocks… После сохранения запускаем (набираем Command → Create Simulation, затем Command →Start).

Мы получили классическую модель системы массового обслуживания. После получения результата занесем его в таблицу (Exel). Повторим моделирование для другого закона распределения случайной величины. GENERATE (NORMAL (1, 14, 5)) SEIZE T ADVANCE (EXPONENTIONAL (1, 0, 10)) RELEASE T TERMINATE 1 START 100 Необходимо следить за состоянием очереди

и средним временем нахождения в очереди. При наличии большой очереди изменим время работы сервера. Подберем оптимальную конфигурацию. В результате REPORT информация о среднем времени обслуживания дается в столбце AVE. TIME, а коэффициент использования канала – UTIL. Далее продолжаем аналогичным способом проводить моделирование для других законов распределения. Для гауссовского закона распределения запишем модель.

GENERATE (NORMAL (1, 14, 5)) SEIZE T ADVANCE (NORMAL (1, 12, 4)) RELEASE T TERMINATE 1 START 100 Здесь закон NORMAL (1, 14, 5) означает гауссовское распределение с математическим ожиданием 14 единиц, а стандартное (среднее квадратическое) отклонение 5 ед. Аналогично для сервера. Опять определяем очередь. Оптимизируем модель и далее продолжаем…

Программа GPSS World Проводим аналогичное моделирование для гамма-распределения случайных величин. GENERATE (GAMMA (1, 0, 12, 2)) SEIZE T ADVANCE (GAMMA (1, 0, 10, 2)) RELEASE T TERMINATE 1 START 100 Все исследуем по аналогичной методике. Результат заносим в таблицу. Оптимизируем модель и далее продолжаем…

Программа GPSS World Моделируем распределение Пирсона 5. GENERATE (PEARSON 5 (1, 0, 12, 2)) SEIZE T ADVANCE (PEARSON 5 (1, 0, 10, 2)) RELEASE T TERMINATE 1 START 100 Опять подбираем оптимальную конфигурацию. Продолжаем дальше.

Программа GPSS World Опять подбираем оптимальную конфигурацию. Далее продолжаем аналогично для сочетания распределений. GENERATE (NORMAL (1, 20, 2)) SEIZE T ADVANCE (PEARSON 5 (1, 0, 10, 2)) RELEASE T TERMINATE 1 START 100 Продолжаем дальше.

Программа GPSS World Поступление транзактов по экспоненциальному закону, а обслуживание – по Пирсону 5 GENERATE (EXPONENTIAL (1, 0, 15)) SEIZE T ADVANCE (PEARSON 5 (1, 0, 10, 2)) RELEASE T TERMINATE 1 START 100 Продолжаем дальше.

Программа GPSS World Опять подбираем оптимальную конфигурацию. Далее продолжаем аналогично. GENERATE (EXPONENTIAL (1, 0, 15)) SEIZE T ADVANCE (NORMAL (1, 10, 3)) RELEASE T TERMINATE 1 START 100 Продолжаем дальше.

Программа GPSS World Для моделирования многоканального устройства создадим новый файл со следующим текстом. T STORAGE 3 GENERATE (EXPONENTIONAL (1, 0, 12)) ENTER T ADVANCE (EXPONENTIONAL (1, 0, 10)) LEAVE T

GPSS World TERMINATE 1 START 100 Для задания других видов распределения используются соответствующие функции. Например, GENERATE (Exponential (1, 0, 10)) задает экспоненциальный закон распределения времени поступления транзактов, при ср. времени -10 единиц. GENERATE (Normal (1, 10, 3)) – нормальный закон распределения с математическим ожиданием 10 и стандартным отклонением 3.

GPSS World На практических занятиях предлагается промоделировать процесс функционирования устройства, включающего несколько составных частей, или процедуры обслуживания разного характера. Это может быть, например, техническая система, выполняющая несколько этапов обработки изделий и, соответственно, включающая несколько средств для реализации обработки, несколько станков, транспортёр, печь, испытательный стенд и т. п.

GPSS World Процедура обслуживания может быть связана с работой торгового отдела из нескольких продавцов, с решением задач в одно- или многопроцессорной вычислительной системе и т. д. Указывается время работы или количество обрабатываемых изделий, решаемых задач и т. д. По результатам моделирования требуется подготовить отчёт в стандартной для GPSS форме (Exel) и проанализировать полученные результаты. Дать рекомендации по совершенствованию исследованной системы.

GPSS World Система GPSS World - это мощная среда компьютерного моделирования общего назначения, разработанная для профессионалов в области моделирования. Это комплексный моделирующий пакет, охватывающий области как дискретного, так и непрерывного компьютерного моделирования, обладающий высочайшим уровнем интерактивности и визуального представления информации. Освоение его – гарантия успеха.

GPSS World На практических занятиях предлагается также различные модификации процессов функционирования. В частности, предлагается включить в программу очередь - QUEUE и задать приоритеты транзактам.

GPSS World

Цели и задачи дисциплины • дискретного управления, • b) знакомство с техническими средствами систем управления, • c) овладение классическими методами анализа, • d) знакомство с основными способами синтеза систем управления, • e) знакомство с современными методами анализа и синтеза динамических систем с использованием типовых пакетов прикладных программ.

Введение • Тео рия управле ния — наука о принципах и методах управления различными системами, процессами и объектами. • Управление большими системами – одна самых перспективных (и сложных) отраслей науки. Эта тема особенно актуальна в управлении техническими и экономическими системами, в когнитивной (cognitio — познание)науке. • Развитие теории управления началось в период промышленной революции, когда решались задачи регулирования, то есть

Предмет теории управления задачи типа поддержания заданного значения частоты вращения, температуры, давления в устройствах (например, в паровых машинах). Отсюда происходит название «теория автоматического регулирования» . • Предмет теории управления – управленческие действия, в которых выражаются социальные, экономические, физические, технические и др. отношения и интересы, проявляющиеся в воздействии на сложную систему (её

Предмет исследования элементы) с целью достижения определенной цели, либо упорядочения, либо развития и совершенствования, максимизации эффекта и т. д. Предметом являются также вопросы развития практики управления, методы и технологии управления и т. п. Теория управления имеет свой, только ей присущий предмет исследований — она изучает закономерности организации управленческого процесса и возникающие во время этого процесса отношения между

Введение. Теория управления элементами системы (техническими, юридическими лицами, объектами хозяйственной деятельности или людьми и т. д. ), определяет методологические приемы, соответствующие специфике объекта исследований, разрабатывает систему и методы активного воздействия на объект управления и определяет способы предвидения и прогнозирования изучаемых процессов. Регистрация и систематизация явлений, раскрытие закономерностей и определение причинных связей между

Предмет исследования ними для разработки практических выводов и рекомендаций — основная задача любой науки, в том числе и науки управления. • В любой управляемой системе есть, как минимум, два объекта – управляемый и управляющий. Пример: автопилот, АЭС. • В сложных системах поддержание их существования (функционирования) обеспечивается, в основном, за счет управления. Управление по сути является процессом переработки информации. В

Введение реальных сложных системах кроме каналов информации, устройств переработки информации и подобных им в управлении принимают участие и другие составляющие, поэтому вся совокупность элементов называется управляющим комплексом сложной системы. • Поиск оптимальных методов управления сложными системами ведется постоянно и в большом диапазоне, от технологических до экономических, административных и даже социально-психологических.

Метод управления можно определить как способ воздействия на управляемую систему на любых уровнях для реализации поставленных задач. Управление должно осуществляться таким образом, чтобы режимы функционирования системы обладали требуемыми свойствами. В связи с этим, принятие решений и выработка управляющих воздействий осуществляются, обычно, путем достижения некоторого экстремума для так называемого критерия управления (целевая функция).

Централизованное и децентрализованное Управление в сложной системе может быть централизованным и децентрализованным. Рассмотрим управление полетами – экипажи связаны с пунктом управления полетами. Это – централизованное управление. Здесь очень важен правильный выбор степени централизации управления. Децентрализация управления позволяет сократить объем перерабатываемой информации, но приводит к снижению качества управления.

Введение Отмеченные трудности в значительно меньшей степени проявляются в системах управления с иерархической структурой. Для управления с иерархической структурой (см. слайд иерархической системы) характерно наличие нескольких уровней управления. Весьма широкий класс реальных систем имеют иерархическую структуру. Методы управления зачастую дополняют друга, выбор их ориентирован на

Введение экономическую целесообразность, своевременность и доступность каких-либо из основных методов. • Решение проблем управления сложными системами связано со значительными трудностями, так как наряду с процессами, которые поддаются количественным измерениям (параметры системы, затраты ресурсов в количественном и стоимостном выражении, расход энергии, расход сырья, металлоемкость и пр. ), есть и такие, что не

Введение поддаются объективной количественной оценке: например, эффективность действующих методов воздействия на коллектив, воздействие моральных стимулов и системы мотиваций на производительность труда, значение административного предвидения и прогнозирования и т. п. Анализ и оценка этих явлений возможны лишь после длительного экспериментирования, например, с помощью имитационного моделирования, с последующей

обработкой полученной информации (результатов). • Процесс управления физическими, технологическими объектами, машинами, станками имеет свои сложности, но такого рода объекты значительно надежнее (не всегда) выполняют команды управления, их действия, алгоритм поведения вполне предсказуемы, а экономические же процессы значительно сложнее. • Рост сложности систем управления

Введение определяется или сложной конструкцией, конкуренцией, стремлением к повышению производительности труда и скорости обработки информации, вводом в эксплуатацию все более сложных и совершенствованием действующих технологических объектов (энергетических и транспортных систем, каналов связи и т. п. ), увеличением количества взаимодействий между элементами экономических, хозяйственных, государственных систем и т. д.

Условия управления Часто система и ее технологический процесс управления осуществляется в условиях неопределенности, при неполноте исходной информации. Однако дефицит информации не является непреодолимым препятствием для принятия управленческого решения или алгоритма. Например, при изменении условий внешней среды предприятие, стремящееся к выживанию и достижению максимальной прибыли, будет адекватно реагировать на эти изменения и механизм

Задачи управления адаптации предприятия, принимаемые в этом случае управленческие решения могут быть многовариантными. Любая задача целеустремленного управления, построения сложной системы, проектирования и т. д. сводится в конечном итоге к выбору лучшего варианта. Различим экстремальные задачи по способу задания вариантов. Если вариант задается с помощью чисел, то это задача

Задачи управления математического программирования. Если имеем набор функций, то соответствующую задачу относят к управлению процессами. Качество варианта определяется целевой функцией. Приведем пример (фирмы). Для подобных систем наиболее типичными задачами управления являются: 1) Управление документацией (документооборот);

Пример. Задачи фирмы 2) Управление работами по организации труда (менеджмент); 3) Управление технико-экономическим планированием, управление финансами; 4) Оперативное управление производством; 5) Управление ремонтным и транспортным обслуживанием; 6) Управление контролем качества; 7) Общее административное руководство.

Классификация и задачи • Задачи систем автоматического управления Рассмотрим (на первом этапе детерминированные) автоматические системы управления. Они применяются для решения в основном трех типов задач: • 1) Стабилизация функционирования системы, то есть поддержание заданного режима работы системы, который не меняется длительное время ( или за рассматриваемый отрезок времени);

Классификация и задачи 2) Программное управление – управление по заранее известной программе (задающий сигнал меняется, но характер его поведения заранее известен); 3) Слежение за неизвестным задающим сигналом. Для решения поставленных задач требуется формальное математическое описание процессов управления в сложных системах. Первым шагом этого является схематизация структуры управления. В этом

Теория управления заключается суть теоретических установок: на основе, например, системного анализа составляется математическая модель объекта управления (ОУ), после чего выявляются факторы, синтезируется алгоритм управления (АУ) для получения желаемых характеристик протекания процесса или целей управления. Об этом будет сказано ниже. • Теория управления базируется на системном анализе (теории систем),
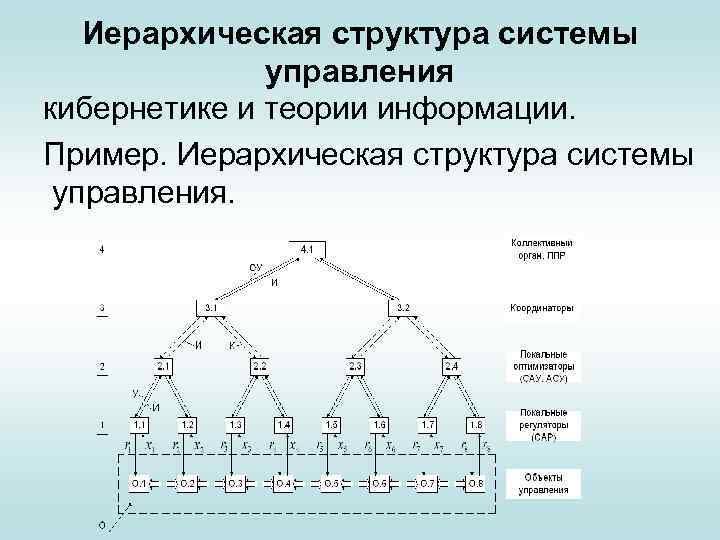
Иерархическая структура системы управления кибернетике и теории информации. Пример. Иерархическая структура системы управления.

Моделирование Теория управления изучает объекты такой сложности, когда приходится привлекать различные традиционные научные дисциплины. Реально содержание еще более глубже. Суть заключается в учете т. н. системного эффекта, когда возможно появление новых свойств. Моделирование – это центральная тема всей дисциплины. О нем будет сказано много. Сейчас же отметим, что модель (лат. modulus - мера) – это объект, замещающий оригинал.

Моделирование Само же моделирование м. б. определено как представление объекта (в нашем случае – системы) в виде некоторой модели для исследования, получения информации об системе. При этом подразумевается, чаще всего, что при моделировании проводятся эксперименты с моделью. Если результаты моделирования подтверждаются и могут быть основой для исследования системы, синтеза, то говорят об адекватной модели.

Типы математических моделей Из вышесказанного ясно, что можно выделить два основных типа математических моделей: дискретные и непрерывные. Существуют также комбинированные дискретно-непрерывные. Дискретные изучаются преимущественно в кибернетике (теория управляющих систем) и опираются на аппарат дискретной математики, а непрерывные - в теориях динамических систем и автоматического управления, математической основой которых

Типы математических моделей является теория дифференциальных уравнений. Об этом будет сказано ниже. Широко применяются (в стохастическом случае) при изучении сложных систем вероятностно-статистические методы - теория массового обслуживания (ТМО), методы стохастического программирования и стохастического моделирования. Несмотря на различие форм и математического аппарата, все эти подходы к описанию сложных систем объединяет общая методология и общий предмет изучения.

Синхронный и асинхронный принципы С точки зрения распределения потоков информации, участвующей в управлении, различают два принципа построения процесса - синхронный и асинхронный. Синхронный процесс состоит из последовательности циклов. При асинхронном новая поступающая информация возможно приводит к прекращению производимых управленческих действий и переходу к выполнению нового алгоритма и т. д.
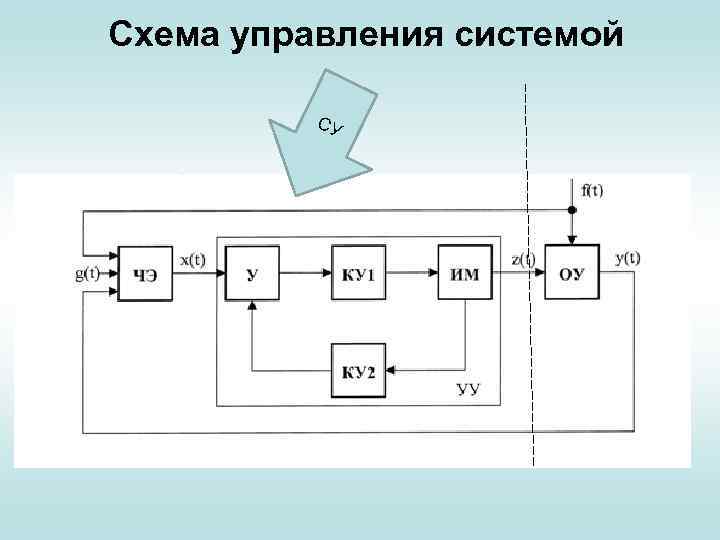
Схема управления системой СУ

Схема управления системой На приведенных схемах обычно не показаны «потребители» или объекты управления. Но на данной схеме все же присутствует объект управления (ОУ), который имеет соответствующие связи. • Задающее воздействие g(t), являющееся входным сигналом или содержит информацию системы управления или подобное, что определяет ход процесса (возможно требуемый закон изменения выходного сигнала z(t)). Это воздействие поступает на приемник - преобразующее

Схема управления системой устройство или чувствительный элемент (ЧЭ). Кроме того на этот элемент подаются сигналы обратной связи у(t) и, возможно, возмущающего воздействия f(t). • С выхода приемника сигнала (их может быть насколько) соответствующим образом обработанный сигнал x(t), возможно цифровой, являющийся функцией воздействия {x, y, f} и характеризующий ошибку (рассогласование), поступает на вход усилителя, усиливается (и

Схема управления системой обрабатывается) усилителем (У) и поступает на исполнительный механизм (ИМ). Исполнительным механизмом может являться некоторая система, например, ЭВМ. Выходной сигнал z(t) управляет ОУ. Отметим существование главной обратной связи у(t). Рассмотрим еще один пример системы управления. ( На слайде она обведена пунктиром).
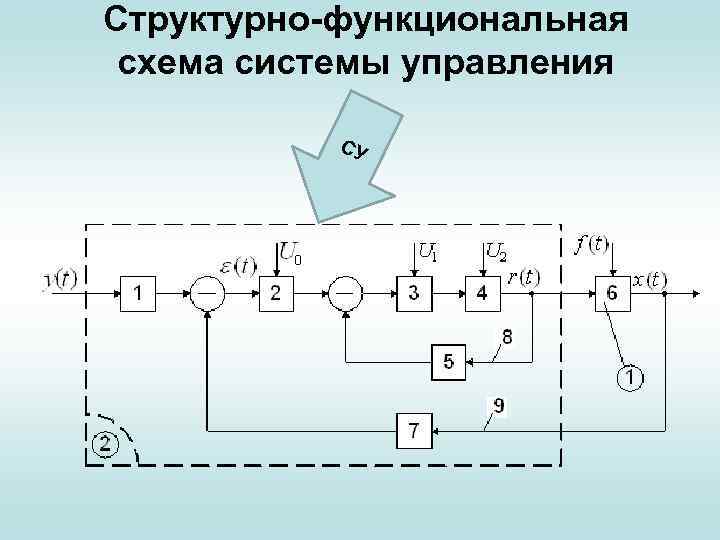
Структурно-функциональная схема системы управления СУ

Пример • Ui - источники энергии (питание). • 1 — чувствительный элемент или преобразующее устройство ; • 2 — микропроцессор (или ЭВМ) (придаёт системе требуемые свойства); • 3 — усилительное устройство; • 4 — исполнительное устройство; • 5 — параллельное корректирующее устройство; • 6 — объект управления; • 7 — элемент (устройство) главной обратной связи; • 8 — местная обратная связь; • 9 — главная обратная связь.

Пример Данная система управления — представляет собой замкнутую динамическую систем управления, использующая получающиеся сигналы в процессе работы для управления источниками энергии, стремящаяся сохранить в допустимых пределах ошибки (рассогласования) между требуемыми и действительными значениями регулируемых переменных путем их сравнения и т. д. Рассмотрим другие примеры (экономические).

Управление бюджетом (дохода национального бюджета) • Рассмотрим обобщенную модель системы управления «статьей» дохода бюджета. Будут рассмотрены не все контуры модели. Обратим внимание, что блок «измерение» должен точно и быстро отслеживать изменения, однако в бюрократической системе управления это не всегда удается. • Подобная модель помогает понять «роль правительства» в управлении экономикой.
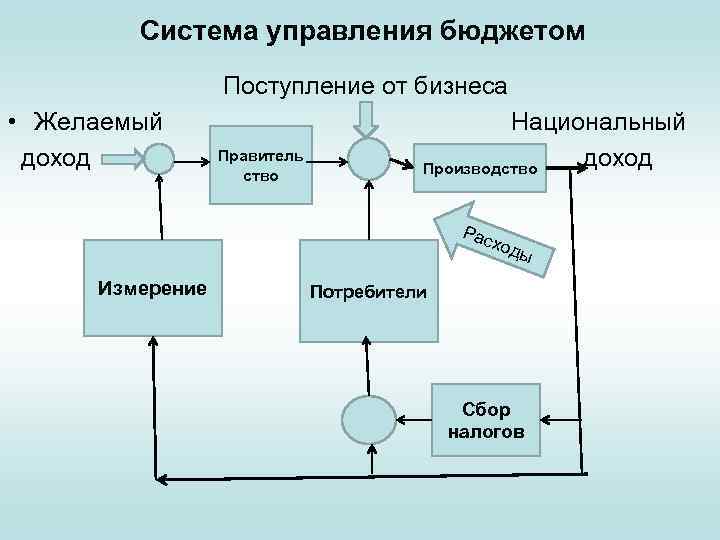
Система управления бюджетом Поступление от бизнеса • Желаемый доход Правитель ство Национальный доход Производство Рас ход ы Измерение Потребители Сбор налогов

Импульсные системы • Рассмотрим еще один пример. Импульсные системы содержат импульсные устройства ( см. следующий слайд –позиция 2), осуществляющие квантование сигналов по времени (АИМ). • Импульсное устройство, замыкаясь в дискретные равноотстоящие моменты времени (t = i∙T, i = 0, 1, 2, …, где i — период повторения, а T — период дискретности), преобразует непрерывный входной сигнал в дискретный. Здесь также имеется обратная связь. • Типовая структура импульсных систем представлена на следующем слайде.
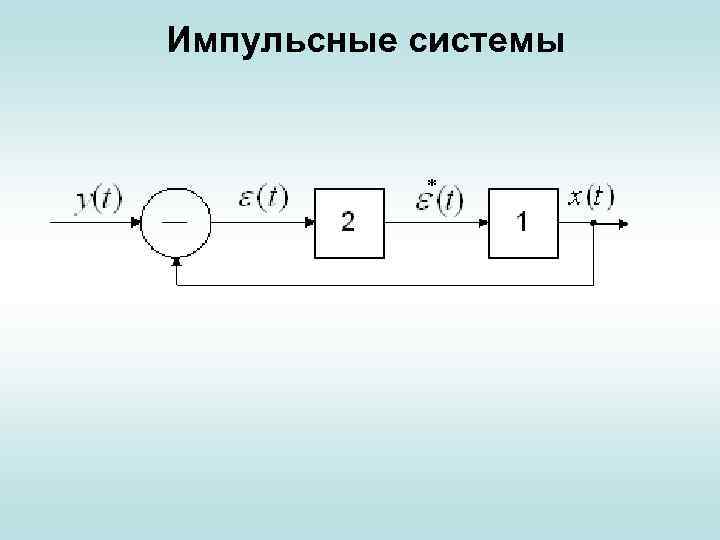
Импульсные системы
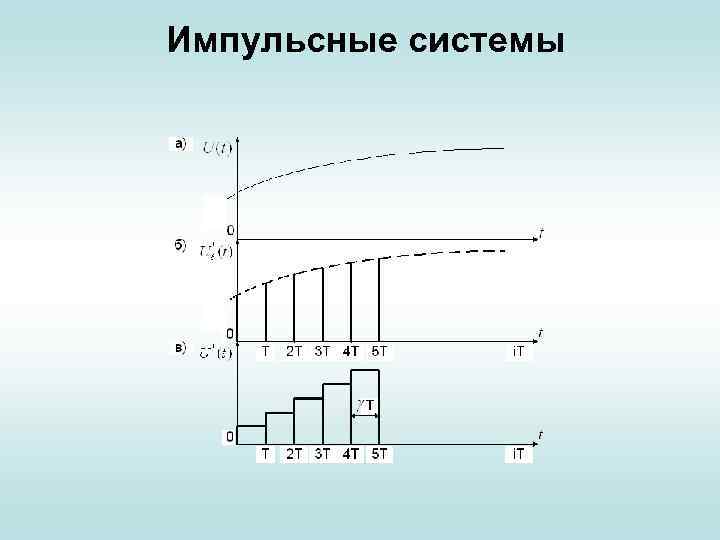
Импульсные системы

Общие требования, предъявляемые к системам • Кратко перечислим основные требования, предъявляемые при исследовании и проектировании систем управления: • 1) к качеству управления; • 2) к устойчивости; • 3) к точности; • 4) к управляемости; • 5) к наблюдаемости; • 6) к условиям эксплуатации; • 7) к стоимости; • 8) к др. • Эти требования раскрываются при моделировании.
СИНТЕЗ СИСТЕМЫ

Синтез системы управления • Первый шаг процесса синтеза – это определение назначения системы. • Второй шаг – это указать те переменные, те рычаги, которые подлежат управлению. • На третьем шаге следует предъявить требования к точности. • Наконец, необходимо выбрать систему измерения, которая измеряет выбранные переменные (с требуемой точностью и т. д. ).

Синтез системы управления • Заключительный этап процедуры синтеза состоит в настройке параметров системы. Если в результате всего этого достигается желаемое качество управления, то процесс синтеза на этом заканчивается. В противоположном случае меняется конфигурация системы и все этапы синтеза повторяются. • Сколько подходов возможно при этом?

Например, Боинг – 777 был около 2400 раз испытан с помощью компьютерного моделирования прежде чем был построен в железе первый прототип. Рассмотрим более подробно требования к качеству системы управления. Это очень важно. В управлении сложными системами качество конкурирует с устойчивостью системы. Мы не говорим о работоспособности. Система управления может быть устойчивой, но не качественной. (Не исключено, что система окажется качественной, но неустойчивой).

Требования, предъявляемые к системам- качество • Оценка качества управления является одной из наиболее важных сторон общей оценки эффективности всей системы. • Качество управления сложными системами зависит от многочисленных факторов. Наиболее существенные кратко можно свести в четыре группы: • 1) факторы, связанные с качеством критериев управления; •

Требования, предъявляемые к системам- качество • 2) факторы, определяющие динамику (частоту циклов) управления; • 3) факторы, характеризующие качество обрабатываемой информации; • 4) факторы, связанные с качеством алгоритма (оператора, функционала) управления.

Требования, предъявляемые к системам- качество • Воздействие управляющей информации можно описать (к сожалению, не всегда) с помощью некоторых параметров. Если речь идет об экстремальном управлении, то значения этих параметров выбираются так, чтобы критерий управления (или целевая функция) достигали при определенных условиях максимума/ минимума. • Т. е. в качестве критерия управления следует выбирать сам показатель эффективности. Однако в реальных системах далеко

не всегда удается это сделать, т. к. показатель эффективности системы может описываться очень сложными соотношениями, затрудняющими решение упомянутых экстремальных задач. Более того, упомянутые соотношения могут быть вообще просто неизвестными. Существуют и другие соображения, вынуждающие принимать в качестве критерия управления величину, отличную от показателя эффективности системы. (Все это познается на практике).

Требования, предъявляемые к системам- качество Поэтому в реальных системах эффективность функционирования системы управления может отклоняться от экстремальных значений. Проблема качества управления в общем виде еще не достаточно исследована. Рассмотрим остальные требования. Рассмотрим понятие устойчивости системы. Что понимается под устойчивостью системы управления?

Требования, предъявляемые к системам- устойчивость • В системах управления часть энергии (информация) с выхода системы подаётся на вход (обратная связь). Энергия (система)не может изменяться мгновенно, кроме того существуют запаздывания, или замедленная реакция. Поэтому, при определённых условиях система может выйти за пределы, то есть оказаться неустойчивой. • Устойчивость определяет «свободное» движение системы, когда внешнее воздействие отсутствует. Важно определить поведение системы при наличии таковых. Поэтому анализируют качество управления при наиболее неблагоприятных или типовых воздействиях: например, резкого скачка,

Требования, предъявляемые к системам- устойчивость типа единичного ступенчатого воздействия, когда неожиданно возникает воздействие. Система может при этом реагировать не адекватно. • Итак, при функционировании системы в условиях, отличающихся от нормальных, существенно знать, сохраняются ли при возмущениях требуемые свойства системы. Под устойчивостью системы управления понимают ее способность сохранять требуемые свойства в условиях действия возмущений. Все это относится не только к системам управления, но и к общим системам. К сожалению, словесное описание не точно. Здесь на помощь приходит математика.

Требования, предъявляемые к системам- устойчивость • С точки зрения моделирования формальные определения устойчивости связаны с некоторым классом систем (динамических), описываемым обыкновенными дифференциальными уравнениями. Что бы это описать более подробно нам надо обратиться к математическому моделированию. На первом этапе мы, как всегда, рассматриваем детерминированный случай. Итак, рассмотрим математические модели систем. Они позволяют более точно

Математические модели систем описать устойчивость, адаптивность и др. Динамика систем очень часто описывается дифференциальными уравнениями. Заметим, что большинство реальных систем является нелинейными, что значительно усложняет задачу. На помощь здесь приходят методы линеаризации, которые мы кратко рассмотрим. Для связи между выходом и входом системы мы будем использовать так называемые передаточные функций. Эта связь не всегда явна.

Математические модели систем управления Итак, имеются следующие основные виды математических моделей систем управления: • 1) линейные; • 2) нелинейные. • В свою очередь каждая из них может быть: • 1) Непрерывной (описывается системой дифференциальных или интегро-дифференциальных уравнений);

Математические модели систем управления • 2) Дискретной (система разностных уравнений); • 3) Дискретно-непрерывной (сочетание непрерывной и дискретной систем). • В свою очередь каждая из них может быть: • 1) Стационарной; • 2) Нестационарной.

Математические модели систем управления • Математическая модель нестационарна, если хотя бы один из параметров системы изменяется с течением времени. • Далее, каждая из них может быть: • 1) С сосредоточенными параметрами; • 2) С сосредоточенными и распределёнными параметрами. • 1) Физические параметры системы (например, масса, скорость, потенциал и др. ) обычно сосредоточены в точке

Математические модели систем управления (либо в точках – так приблизительно можно считать, а возможно и рассредоточено). В этом случае коэффициенты дифференциальных уравнений зависят от этих координат, параметров и т. д. Если рассматривать характеристики системы, сосредоточенные в точках, то в результате, математическая модель будет, например, системой дифференциальных уравнений в полных производных, или подобная ей.

Математические модели систем управления • 2) Если система содержит хотя бы одну из подсистем (например, канал связи, подсеть и т. д. ), параметры которой распределены в пространстве, то математическая модель такой системы уже не может быть записана в полных производных, а возможно будет содержать, например, систему дифференциальных уравнений в частных производных ( ) и т. п.

Математические модели систем управления • В свою очередь математические модели системы (систем управления) могут принадлежать к одному из двух классов: • 1) Детерминированные; • 2) Стохастические или со случайными параметрами (если хотя бы один из параметров или воздействий является случайной функцией или величиной). и др.

Математические модели систем управления • Дифференциальные уравнения, описывающие системы, получаются на основе фундаментальных законов природы. Если мы возьмем для примера RLC– цепь (сл. слайд), то она будет описана следующим уравнением: • Решение этого уравнения м. б. получено классическим методом (мы не будем этим заниматься). Однако отметим очень важное свойство.
RLC-цепь

Математические модели Это же уравнение будет описывать динамику груза с трением. Подобные системы с похожими уравнениями встречаются среди множества электрических, механических, тепловых, гидравлических систем. Изменения соответствующих величин будет иметь типичный характер, представленный на рисунке.

Математические модели Все вышесказанное позволяет распространить решение, полученное для одной системы, на все подобные системы (они так и называются – «подобными» ). В связи с этим очень часто результаты, полученные при анализе электрических систем применяют для изучения других систем. Дифференциальные уравнения линейных динамических элементов с сосредоточенными параметрами (электрическими) приведены на следующем слайде. Они представляют собой аппроксимацию реального поведения элементов.

Дифференциальные уравнения идеальных (электрических) элементов

Принципы линеаризации Очень многие системы являются линейными в некотором диапазоне изменения переменных. Линейность состоит из аддитивности и однородности. С математической точки зрения необходимым условием линейности системы является соответствующая связь между возмущением (на входе) и реакцией системы (на выходе). Если к системе, находящейся в покое, приложить возмущение х1 , то на выходе появится реакция – у1. Если же при тех же условиях на входе появится возмущение х2 , то на выходе появится реакция – у2. Необходимым условием линейности системы

Принципы линеаризации является то, чтобы при возмущении х1 + х2 система давала реакцию у1 + у2. Это положение называют принципом суперпозиции. Очень многие системы не являются линейными даже при малых воздействиях, но многие из них удается линеаризовать. Рассмотрим общий случай, когда некоторая система (точнее элемент) характеризуется возмущением х(t) и реакцией на него у(t). Предположим, что связь между переменными определяется уравнением у(t)=g[х(t)]. Предположим, что рабочая точка равна х0. Тогда в окрестности рабочей точки можно получить ряд Тейлора:

Принципы линеаризации Значение производной g’ характеризует наклон касательной в т. х0. Эта касательная служит хорошей аппроксимацией исходной функции в случае малых значений (х-х0). В таком предположении можно записать: где m- тангенс угла наклона касательной.

Принципы линеаризации Окончательно можно записать у= т х. Если переменная у зависит от нескольких возмущений, то функциональная зависимость имеет вид g(х1, х2, …, хn). Здесь также можно применить разложение в окрестности рабочей точки х0 в ряд Тейлора: где х0 =(х10, х20, х30, …)- рабочая точка.
Преобразование Лапласа

Преобразование Лапласа Возможность линеаризации позволяет использовать аппарат т. н. преобразования Лапласа. Метод преобразования Лапласа позволяет применить при решении дифференциального уравнения решение алгебраического уравнения. В таком случае определение реакции исследуемой системы на входное воздействие подразумевает: 1) получение дифференциальных уравнений; 2) преобразование Лапласа этих дифференциальных уравнений; 3) решение полученных уравнений.

Преобразование Лапласа L функции, например, времени f(t) определяется выражением: Обратное преобразование Лапласа имеет вид: Обычно используют таблицы преобразований (можно найти на сайте МСS)

Преобразование Лапласа

Преобразование Лапласа Переменную s (или р)в преобразование Лапласа можно рассматривать как оператор дифференцирования. Обратное преобразование Лапласа обычно находят путем разложения F(t) на простые дроби. Это позволяет выявить влияние каждого корня характеристического уравнения. Проиллюстрируем метод преобразования Лапласа на примере механической системы: Нам необходимо получить решение, т. е. у(t). Преобразование Лапласа имеет вид:

Преобразование Лапласа Если r(t)=0, у(0)=у0 и у’(0) =0, то получаем: Выражая отсюда Y(s), получим:

Преобразование Лапласа Если полином q(s), стоящий в знаменателе, приравнять нулю, то получим характеристическое уравнение. Его корни называют полюсами системы. Корни р(s), стоящего в числителе, называют нулями системы. Расположение нулей и полюсов (на s– плоскости)характеризует движение системы. Предположим, например, что k/M=2 и b/M=3. Тогда наше выражение примет вид: Положение полюсов полученной функции можно определить, разложив ее на элементарные дроби:

Преобразование Лапласа где k 1 и k 2 - коэффициенты разложения. Коэффициенты разложения являются вычетами функции-образа. Если, не нарушая общности, положить у0 =1, то получим k 1 =2 и k 2=-1. После того, как нашли коэффициенты k 1 и k 2, применяем обратное преобразование Лапласа:

Преобразование Лапласа С помощью таблицы преобразования Лапласа находим решение нашей задачи:

Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной (при условии, что все начальные условия равны нулю). Передаточная функция однозначно описывает динамическую связь между переменными. В предыдущем примере, если все начальные условия положить равными нулю, получим:

Передаточная функция Отсюда находим передаточную функцию как отношение выход/вход: Например, передаточная функция интегрирующей RC -цепочки равна:
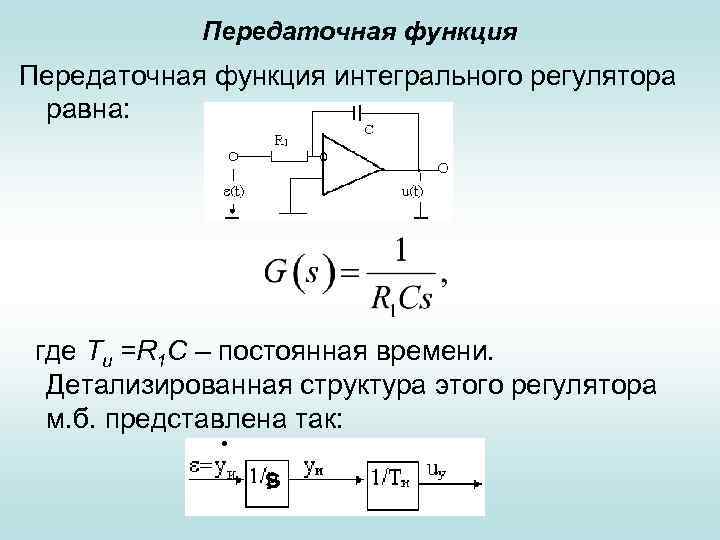
Передаточная функция интегрального регулятора равна: где Ти =R 1 С – постоянная времени. Детализированная структура этого регулятора м. б. представлена так: s

Операционный усилитель относится к важному классу схем, широко используемых в качестве элементов систем управления. Например, передаточная функция пропорциональноинтегрального регулятора равна: где Кп – коэффициент пропорциональности. Его детализированная структура: s

При регулировании по производной и интегралу мы можем получить в итоге воздействие, пропорциональное ошибке, производной и интегралу от ошибки, т. е. : где Кп =R 2/R 1, Tи=R 2 C 2, Tд=R 1 C 1– коэффициенты. С целью снижения уровня помех на выходе системы и повышения устойчивости последовательно с конденсатором C 1 может быть включен дополнительный резистор R 3 (пунктир).

Структурная схема системы в переменных состояния принимает вид: Если в схеме поменять местами резистор R 1 и конденсатор С 1, то получим фильтр с интегрированием, передаточная функция которого равна:
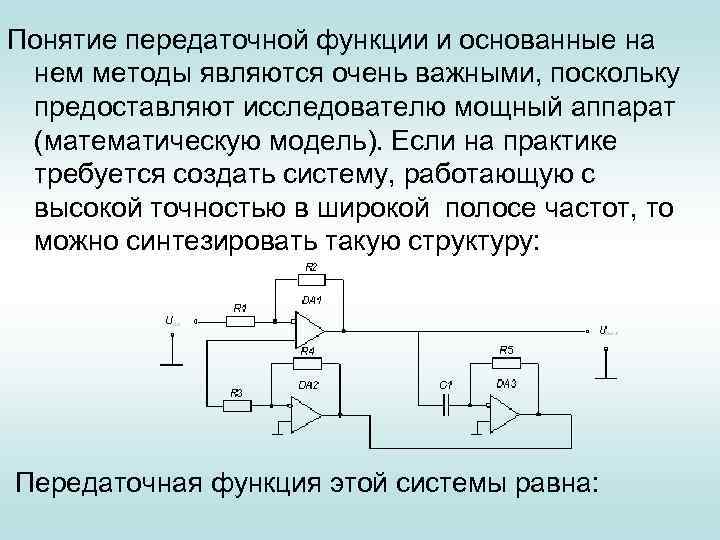
Понятие передаточной функции и основанные на нем методы являются очень важными, поскольку предоставляют исследователю мощный аппарат (математическую модель). Если на практике требуется создать систему, работающую с высокой точностью в широкой полосе частот, то можно синтезировать такую структуру: Передаточная функция этой системы равна:
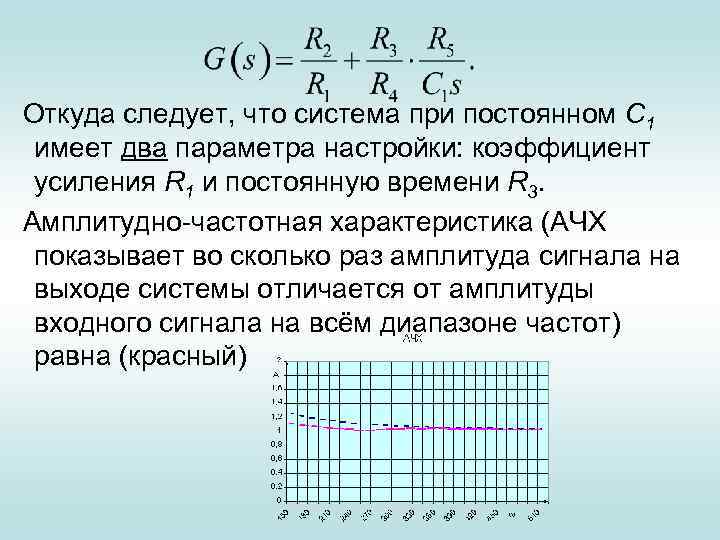
Откуда следует, что система при постоянном С 1 имеет два параметра настройки: коэффициент усиления R 1 и постоянную времени R 3. Амплитудно-частотная характеристика (АЧХ показывает во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне частот) равна (красный)

Амплитудно-частотная характеристика (АЧХ) АЧХ системы означает зависимость модуля её передаточной функции от частоты. В этом случае предполагается подача на вход системы синусоидального тестового сигнала. Выходной сигнал линейной системы также является синусоидальным той же частоты, однако может отличаться по амплитуде и фазе. В случае когда используется логарифмический масштаб, АЧХ превращается в логарифмическую амплитудночастотную характеристику. ЛАЧХ получила широкое распространение в теории автоматического управления в связи с простотой построения и наглядностью при исследованиях.

Амплитудно-частотная характеристика (АЧХ) Передаточную функцию G(s) можно представить в частотной области с помощью соотношения: где R ( ) =Re[G(s)] и X( )=Im[G(s)]. Например, для звуковой карты амплитудночастотная характеристика показывает, как через нее передаются отдельные частотные составляющие аналогового сигнала, что позволяет оценить искажения его спектра. • Идеальная звуковая плата должна одинаково передавать все частоты от 20 до 20000 Гц. Графически это изображается в таком виде
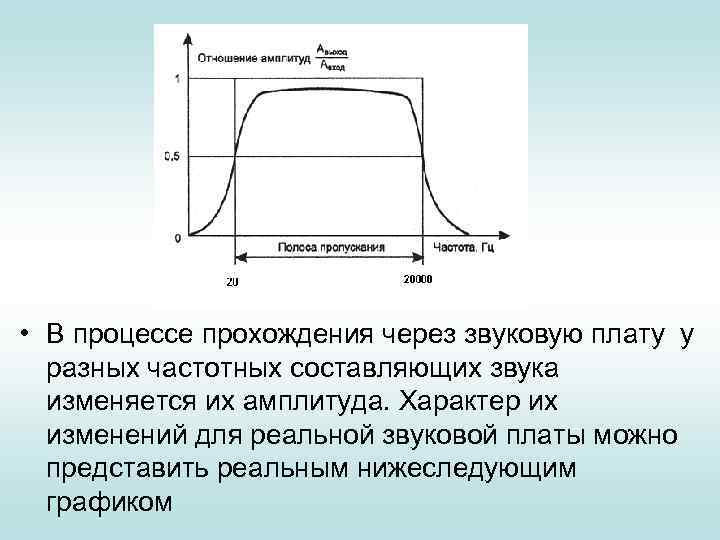
• В процессе прохождения через звуковую плату у разных частотных составляющих звука изменяется их амплитуда. Характер их изменений для реальной звуковой платы можно представить реальным нижеследующим графиком
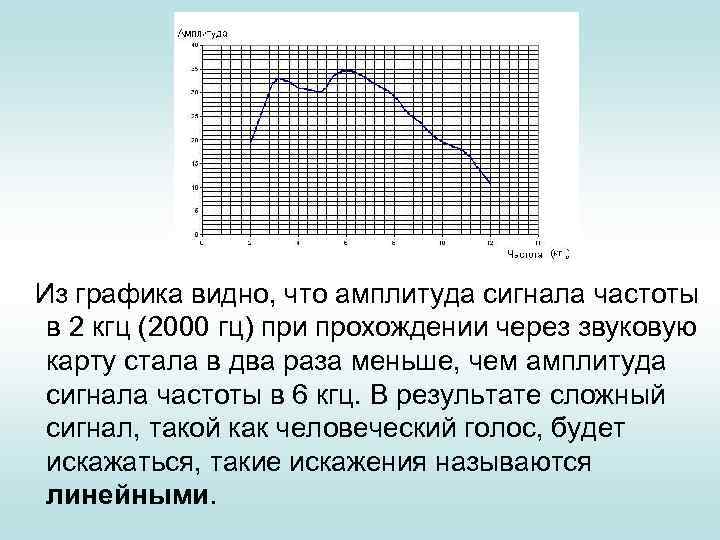
Из графика видно, что амплитуда сигнала частоты в 2 кгц (2000 гц) при прохождении через звуковую карту стала в два раза меньше, чем амплитуда сигнала частоты в 6 кгц. В результате сложный сигнал, такой как человеческий голос, будет искажаться, такие искажения называются линейными.

При искажении АЧХ тембр инструментов или звуков меняется. Отдельные звуки будут звучать громче, чем другие, какие-то фрагменты фонограммы станут незаметными. • Наиболее заметны будут искажения, которые находятся в диапазоне от 1000 до 4500 Гц - в этой области сосредоточена наибольшая часть звуковой информации, и к тому же в этой области наш слух наиболее восприимчив. Наименее заметны перепады АЧХ в области ниже 100 Гц и выше 10 к. Гц. Самыми неприятными моментами являются резкие подъемы АЧХ в районе 2 -3 к. Гц, которые делают звук неприятно резким, и в районе 7 к. Гц, когда звучание приобретает «металлический характер. »

• Отношение сигнал/шум - представляет собой отношение значений (в децибелах) неискаженного максимального сигнала на выходе звуковой платы к уровню шумов электроники, возникающих в собственных электрических схемах платы и т. д. Динамический диапазон. Выраженная в децибелах разность между max и min сигналом, которую плата может пропустить. В идеальной цифровой аудиосистеме динамический диапазон должен быть высок. Для аудио аппаратуры это запас по динамике звука между порогом из шумов и началом перегрузки акустических систем и усилителя. «Классика» требует не меньше 50 д. Б. Рассмотрим еще пример АЧХ.
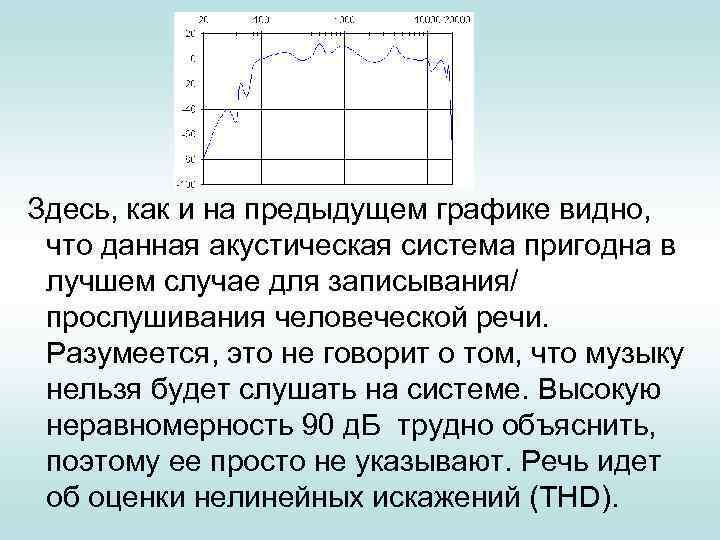
Здесь, как и на предыдущем графике видно, что данная акустическая система пригодна в лучшем случае для записывания/ прослушивания человеческой речи. Разумеется, это не говорит о том, что музыку нельзя будет слушать на системе. Высокую неравномерность 90 д. Б трудно объяснить, поэтому ее просто не указывают. Речь идет об оценки нелинейных искажений (THD).
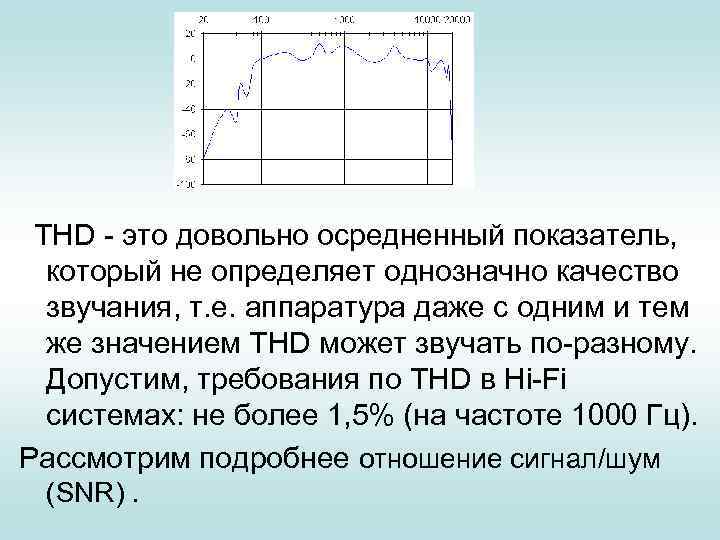
THD - это довольно осредненный показатель, который не определяет однозначно качество звучания, т. е. аппаратура даже с одним и тем же значением THD может звучать по-разному. Допустим, требования по THD в Hi-Fi системах: не более 1, 5% (на частоте 1000 Гц). Рассмотрим подробнее отношение сигнал/шум (SNR).

Шумы можно представить как некий случайный звуковой сигнал малой громкости, который примешан к основному (изначальному) сигналу. • Отношение сигнал/шум показывает превышение уровня сигнала над уровнем шума. Шумы можно также разложить по частотам. В области средних частот шумы наиболее заметны на слух. Наименее неприятен шум, равномерно

распределенный по всем частотам (белый шум). Человек имеет от природы способность отфильтровывать акустический сигнал от шумов, поэтому шумы не так неприятны для восприятия, как искажения (см. THD). Отношение сигнал/шум (SNR) измеряется в д. Б. Для показателя отношения сигнал/шум можно привести следующую примерную табличку: 10 -20 д. Б - Абонентская радио-точка, телефон; 20 -50 д. Б - Колоночки для плеера; 50 -60 д. Б - Переносные радиоприёмники, 8 битные звуковые карты; 60 -80 д. Б - Hi-Fi аппаратура; 80 -100 д. Б - Студийная и Hi-End аппаратура. • Существует некоторое «разночтение» в понятии

сигнал/шум. Фирмы производители любят указывать вместо SNR «немного» другой показатель, а именно - уровень шумов при отсутствии сигнала (Zero Signal Noise). Например, при уровне входного сигнала -80 д. Б сработает выключатель, и уровень шумов падает до фантастических величин, на гране реальности. Отсюда следует заявления о 96 -97 д. Б в дешевой аппаратуре. На поверку, при подаче сигнала с небольшим уровнем, эти характеристики резко падают, становясь хуже на 20… 30 д. Б. Существует более удачный показатель - THD +N, который объединяет два предыдущих (коэффициент нелинейных искажений+шум), что годится для одновременной оценки уровня шумов и искажений.
Устройства для измерения АЧХ Существую специальные устройства для измерения АЧХ.
Структурные схемы

Структурные схемы Преимущество передаточной функции в том, что она позволяет изобразить причинноследственную связь между переменными в наглядной схематической форме. Передаточная функция позволяет охарактеризовать все свойства исследуемой системы. Различные динамические системы представляются в виде структурных схем. Структурные схемы состоят из блоков, каждому из которых соответствует своя передаточная функция. Так, например, на рисунке изображен типовой (разомкнутый) контур системы автоматического регулирования.
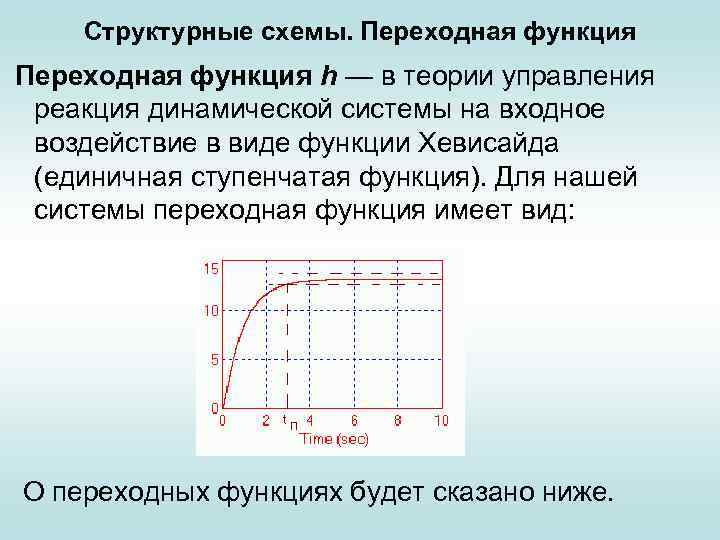
Структурные схемы. Переходная функция h — в теории управления реакция динамической системы на входное воздействие в виде функции Хевисайда (единичная ступенчатая функция). Для нашей системы переходная функция имеет вид: О переходных функциях будет сказано ниже.
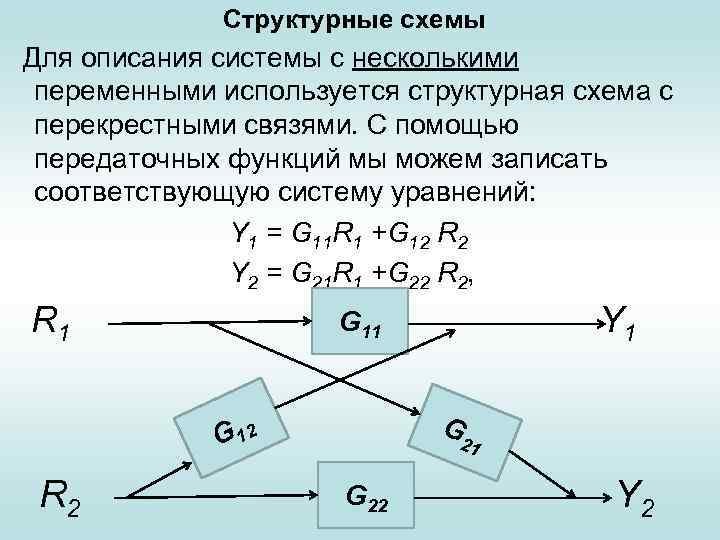
Структурные схемы Для описания системы с несколькими переменными используется структурная схема с перекрестными связями. С помощью передаточных функций мы можем записать соответствующую систему уравнений: Y 1 = G 11 R 1 +G 12 R 2 Y 2 = G 21 R 1 +G 22 R 2, R 1 G G 12 R 2 Y 1 G 11 21 G 22 Y 2

Структурные схемы В матричном представлении подобные системы записываются так: Y= GR Здесь Y, R - соответственно вектора входных и выходных сигналов, а G - матричная передаточная функция (подробнее на сайте МСS). Пользуясь определенными правилами, структурную схему сложной системы можно упростить. Например, можно исключить контур с обратной связью.
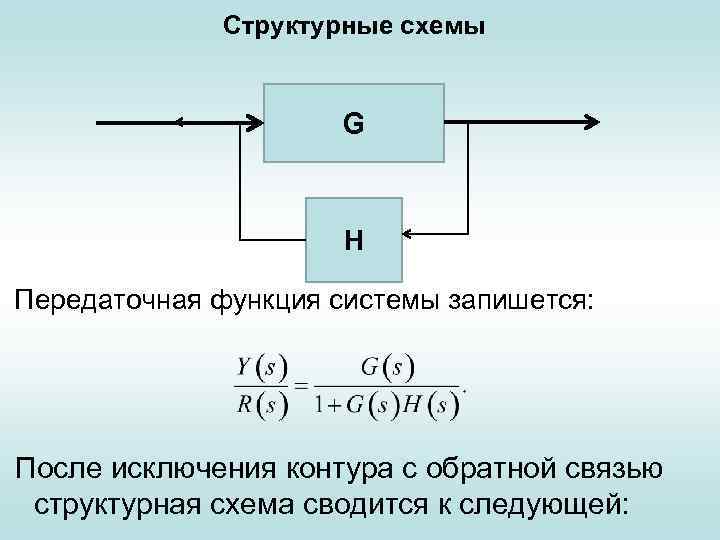
Структурные схемы G Н Передаточная функция системы запишется: После исключения контура с обратной связью структурная схема сводится к следующей:
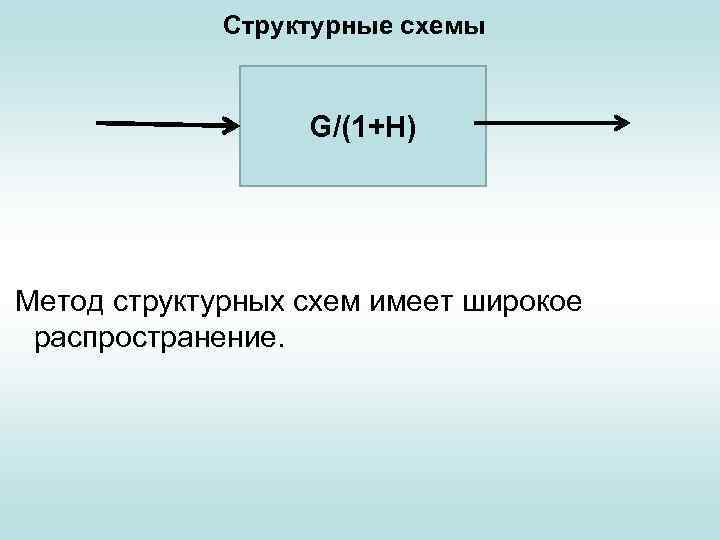
Структурные схемы G/(1+H) Метод структурных схем имеет широкое распространение.
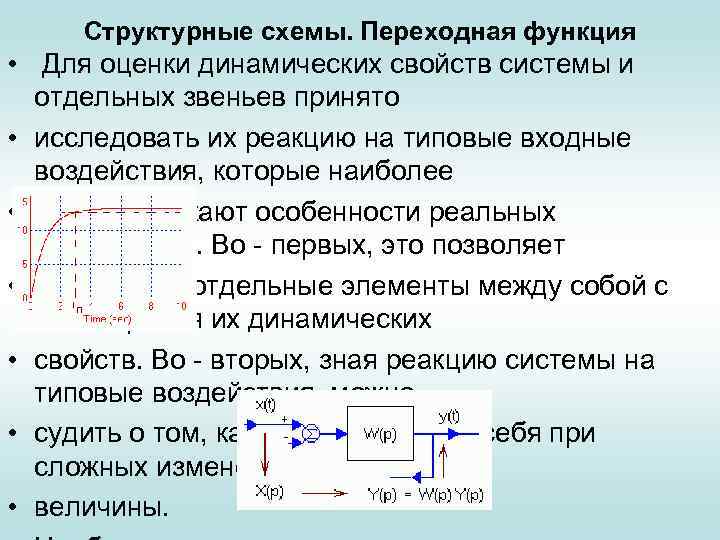
Структурные схемы. Переходная функция • Для оценки динамических свойств системы и отдельных звеньев принято • исследовать их реакцию на типовые входные воздействия, которые наиболее • полно отражают особенности реальных возмущений. Во - первых, это позволяет • сравнивать отдельные элементы между собой с точки зрения их динамических • свойств. Во - вторых, зная реакцию системы на типовые воздействия, можно • судить о том, как она будет вести себя при сложных изменениях входной • величины.

Требования, предъявляемые к системам- качество управления Единичное ступенчатое воздействие: Возможно и смещенное воздействие (и неединичное).
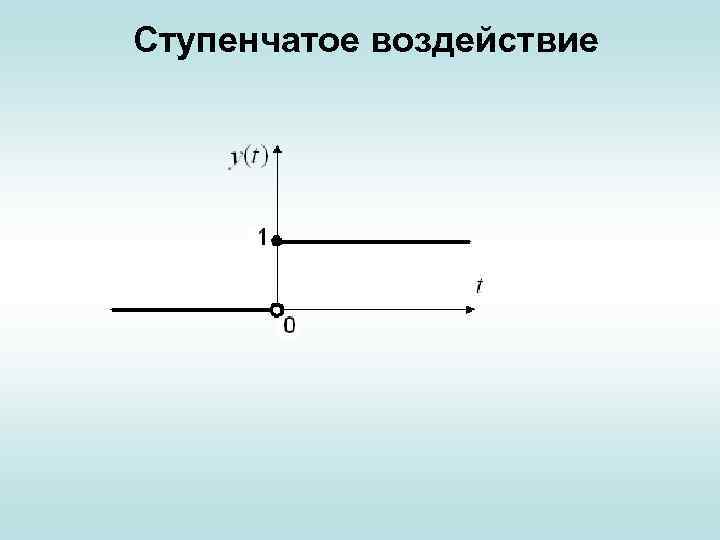
Ступенчатое воздействие

Переходная функция h(t) Передаточная функция (или переходная функция)— один из способов математического описания динамической системы. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал. • В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Переходная функция h(t) – реакция системы на единичное ступенчатое воздействие (дельтафункция): Возможно и смещенное воздействие (и неединичное и т. д. ).

Гармоническое воздействие Гармоническое воздействие: позволяет: • 1) при анализе вынужденного установившегося движения определить частотные характеристики системы. • 2) определив реакцию системы на гармоническое воздействие и разложив периодическое воздействие у(t) в ряд Фурье, определить реакцию системы на это воздействие.

Динамическая точность • Реальные системы работают в условиях, когда воздействия могут быть случайными; при этом отсутствует установившееся состояние в системе, и важно оценить поведение системы в переходном режиме, при отклонениях и т. д. • Тогда в качестве основной характеристики рассматривают динамическую точность. Мерой динамической точности, может служить функционал или среднее значение квадрата ошибки:
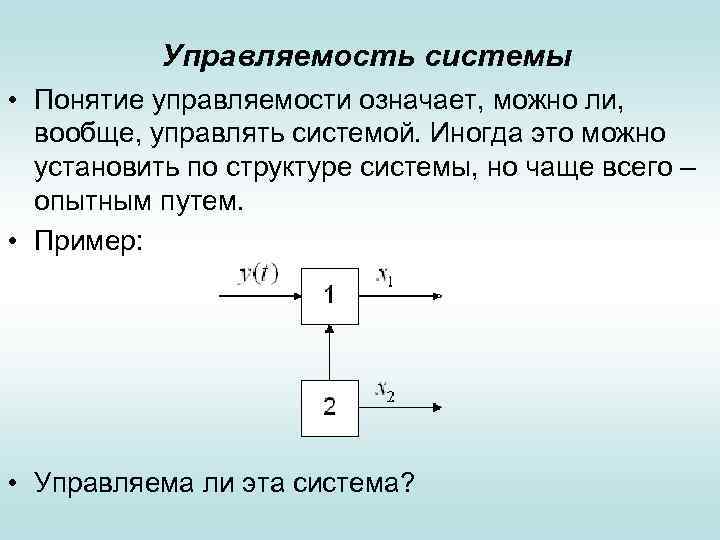
Управляемость системы • Понятие управляемости означает, можно ли, вообще, управлять системой. Иногда это можно установить по структуре системы, но чаще всего – опытным путем. • Пример: • Управляема ли эта система?

Управляемость системы • Система неуправляема, так как невозможно (при данной структуре) воздействовать на вторую подсистему.
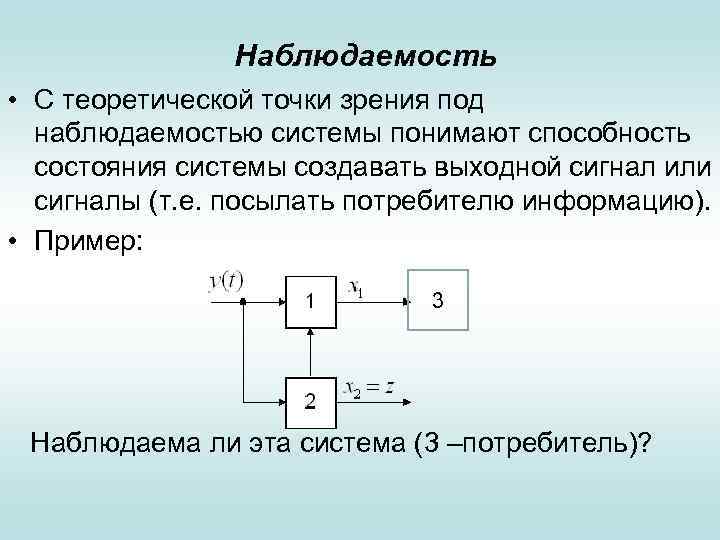
Наблюдаемость • С теоретической точки зрения под наблюдаемостью системы понимают способность состояния системы создавать выходной сигнал или сигналы (т. е. посылать потребителю информацию). • Пример: 3 Наблюдаема ли эта система (3 –потребитель)?

Дискретные математические модели • Решетчатые функции. • Решетчатая функция (РФ) — функция, существующая в дискретны равноотстоящие друг от друга значения независимой переменной и равная нулю между этими значениями аргумента. • Пример такой функции:
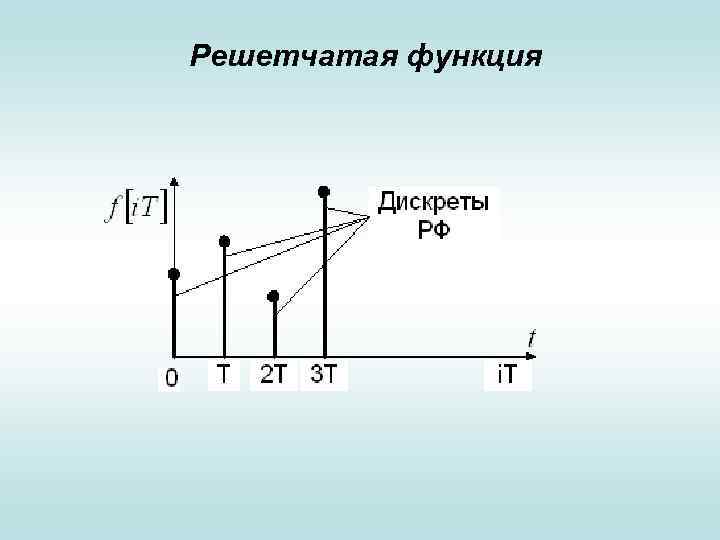
Решетчатая функция
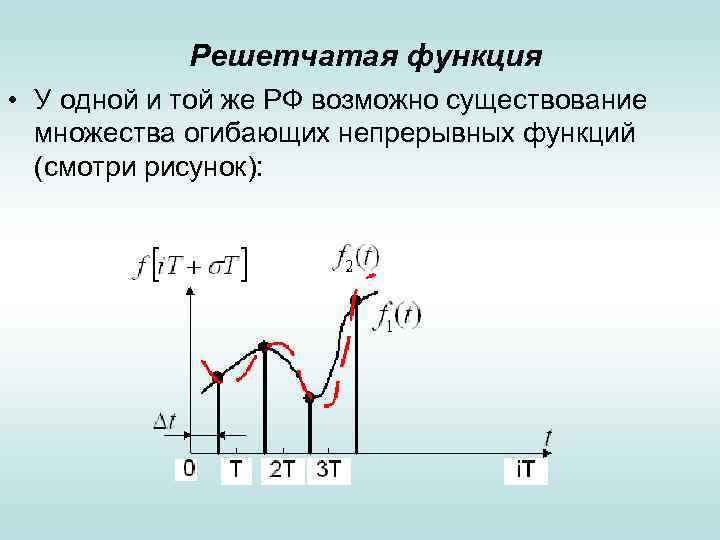
Решетчатая функция • У одной и той же РФ возможно существование множества огибающих непрерывных функций (смотри рисунок):
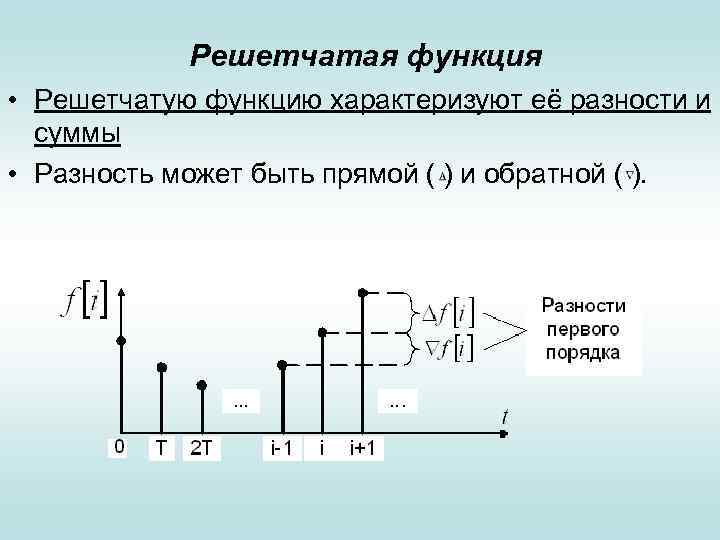
Решетчатая функция • Решетчатую функцию характеризуют её разности и суммы • Разность может быть прямой ( ) и обратной ( ).
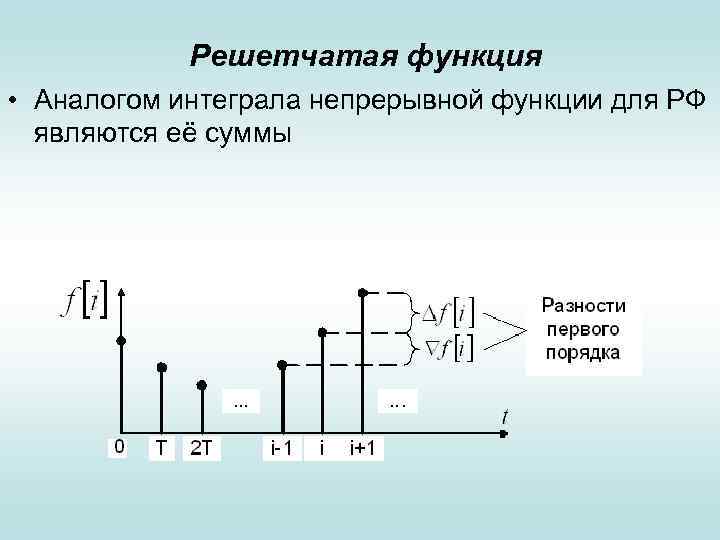
Решетчатая функция • Аналогом интеграла непрерывной функции для РФ являются её суммы
TMO_0_веч_2012.ppt