IMI QUESTION What is foundations of computational mathematics

IMI QUESTION What is ‘foundations of computational mathematics’? FOCM 2002

IMI FOCM DATA COMPRESSION ADAPTIVE PDE SOLVERS FOCM 2002

IMI COMPRESSION - ENCODING DATA SET BIT STREAM Image Signal Surface 1100111100. . . Function f B(f)=(B 1, …, Bn) FOCM 2002

IMI COMPRESSION - ENCODING 1100111100. . . f B(f)=(B 1, …, Bn) FOCM 2002

IMI DECODER BIT STREAM FUNCTION B g. B B Image Signal Surface FOCM 2002

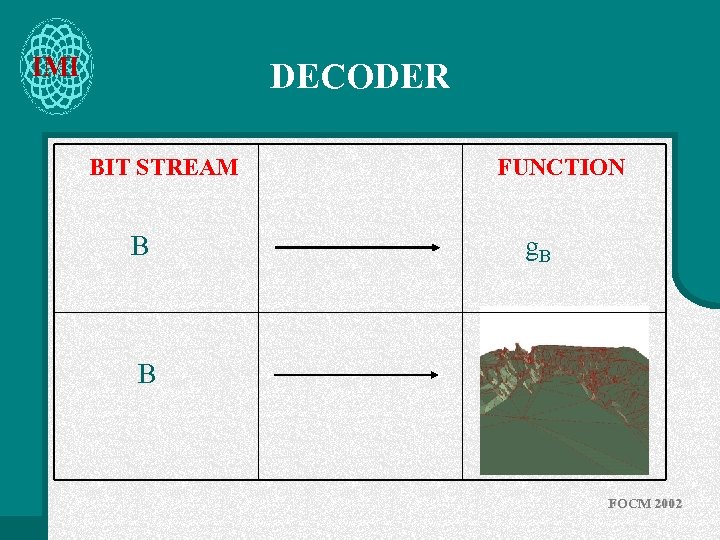IMI DECODER BIT STREAM B FUNCTION g. B B FOCM 2002

IMI Who’s Algorithm is Best? · Test examples? · Heuristics? · Fight it out? · Clearly define problem (focm) FOCM 2002

IMI MUST DECIDE · METRIC TO MEASURE ERROR · MODEL FOR OBJECTS TO BE COMPRESSED FOCM 2002

IMI IMAGE PROCESSING Model Metric “Real Images” “Human Visual System” Stochastic Mathematical Metric Deterministic Smoothness Classes K Lp. Lp Norms FOCM 2002

IMI · Kolmogorov Entropy Given > 0, N (K) smallest number of balls that cover K FOCM 2002

IMI · Kolmogorov Entropy Given > 0, N (K) smallest number of balls that cover K FOCM 2002

IMI Kolmogorov Entropy · Given > 0, N (K) smallest number of balls that cover K · H (K): = log (N (K)) Best encoding with distortion of K FOCM 2002

IMI ENTROPY NUMBERS dn(K) : = inf { : H (K) n} · This is best distortion for K with bit budget n · Typically dn(K) n-s FOCM 2002

IMI · · SUMMARY Find right metric Find right classes Determine Kolmogorov entropy Build encoders that give these entropy bounds FOCM 2002

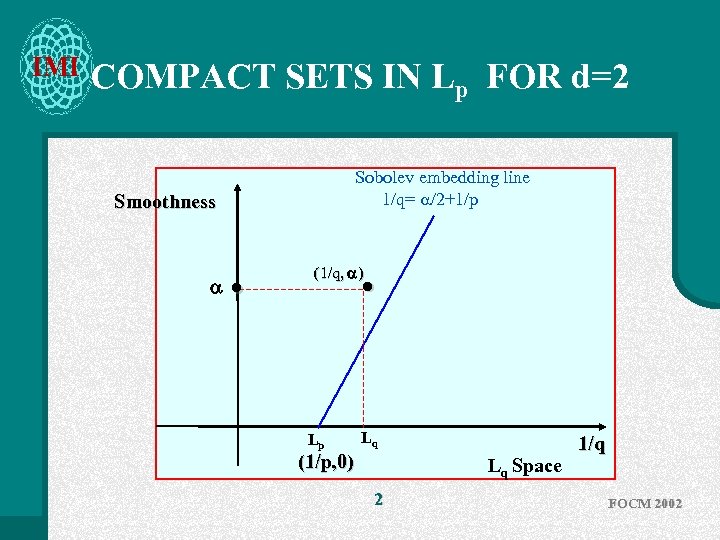IMI COMPACT SETS IN Lp FOR d=2 Sobolev embedding line 1/q= /2+1/p Smoothness • (1/q, ) • Lp Lq (1/p, 0) Lq Space 2 1/q FOCM 2002

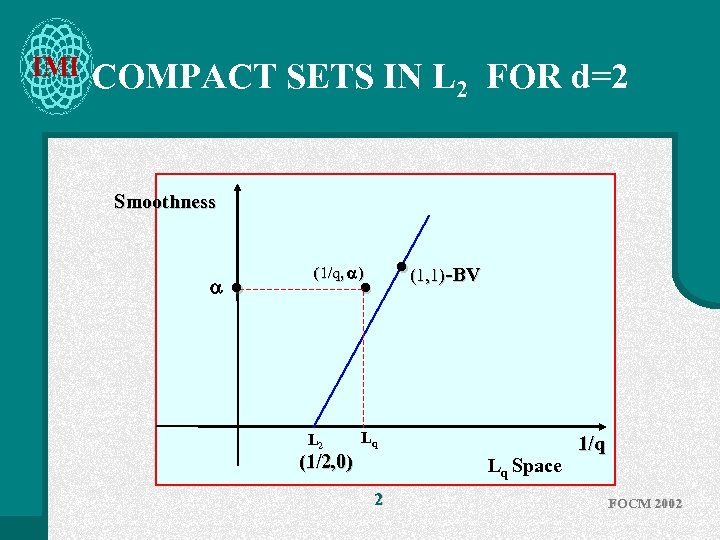IMI COMPACT SETS IN L 2 FOR d=2 Smoothness • • (1, 1)-BV (1/q, ) • L 2 Lq (1/2, 0) Lq Space 2 1/q FOCM 2002

IMI ENTROPY OF K Entropy of Besov Balls B (Lq ) in Lp is n d Is there a practical encoder achieving this simultaneously for all Besov balls? ANSWER: YES Cohen-Dahmen-Daubechies-De. Vore wavelet tree based encoder FOCM 2002

COHEN-DAUBECHIESDAHMEN-DEVORE IMI · · Partition growth into subtrees D j : =T j T j-1 Decompose image f=S j SD I j c I y. I [T 0 | B 0 | S 0 | T 1 | U 1 | B 1 | S 1 | T 2 | U 2 | B 2 | S 2 | Lead tree & bits Level 1 tree, update & new bits, signs Level 2 tree, update & new bits, signs . . . ] FOCM 2002

IMI · · WHAT DOES THIS BUY YOU? Explains performance of best encoders: Shapiro, Said-Pearlman Classifies images according to their compressibility (De. Vore-Lucier) Handles metrics other than L 2 Tells where to improve performance: Better metric, Better classes (e. g. not rearrangement invariant) FOCM 2002

IMI DTED DATA SURFACE Grand Canyon FOCM 2002

IMI POSTINGS Postings Grid Z-Values FOCM 2002

IMI · FIDELITY L 2 metric not appropriate FOCM 2002

IMI · · FIDELITY L 2 metric not appropriate L better FOCM 2002

IMI OFFSET If surface is offset by a lateral error of , the L norm may be huge L error FOCM 2002

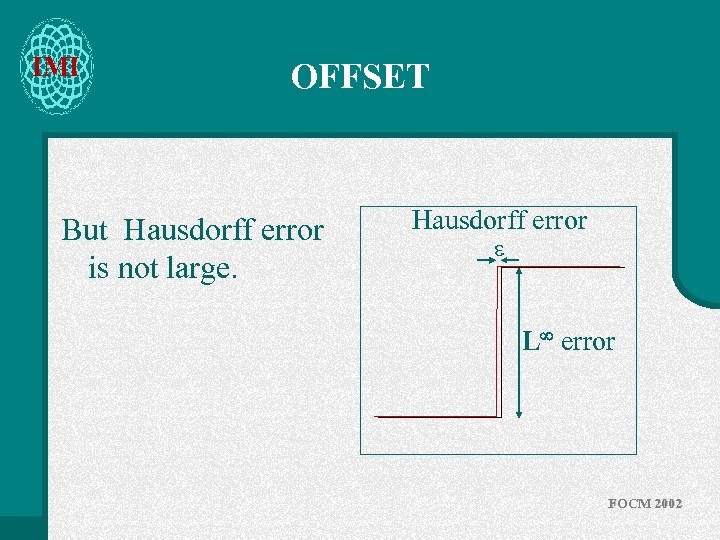IMI OFFSET But Hausdorff error is not large. Hausdorff error L error FOCM 2002

IMI CAN WE FIND dn(K)? · K bounded functions : d. N(K) n-1 for N=nd+1 · K continuous functions: d. N(K) n-1, for N= nd log n · K bounded variation in d=1: dn(K) n-1 · K class of characteristic functions of convex sets dn(K) n-1 FOCM 2002

IMI Example: functions in BV, d=1 Assume f monotone; encode first (jk) and last (j k) square in column. Then k |jk-j k| M n. Can encode all such jk with C M n bits. j k jk k FOCM 2002

IMI · · · ANTICIPATED IMPACT DTED Clearly define the problem Expose new metrics to data compression community Result in better and more efficient encoders FOCM 2002

IMI NUMERICAL PDEs u solution to PDE uh or u n is a numerical approximation uh typically piecewise polynomial (FEM) un linear combination of n wavelets different from image processing because u is unknown FOCM 2002

IMI · · MAIN INGREDIENTS Metric to measure error Number of degrees of freedom / computations Linear (SFEM) or nonlinear (adaptive) method of approximation using piecewise polynomials or wavelets Inversion of an operator Right question: Compare error with best error that could be obtained using full knowledge of u FOCM 2002

IMI EXAMPLE OF ELLIPTIC EQUATION POISSON PROBLEM FOCM 2002

CLASSICAL ELLIPTIC THEOREM IMI Variational formulation gives energy norm Ht . . ) THEOREM: If u in Ht+s then SFEM gives ||u-uh ||Ht < hs |u|Ht+s h 8 Can replace Ht+s by Bs+t (L 2 ) Approx. order hs equivalent to u in Bs+t (L 2 ) 8 FOCM 2002

IMI HYPERBOLIC ) Conservation Law: ut + divx(f(u))=0, u(x, 0)=u 0(x). . THEOREM: If u 0 in BV then ||u(, , t)-uh(. , t)|| < h 1/2 |u 0| BV L 1 u 0 in BV implies u in BV; this is equivalent to approximation of order h in L 1 FOCM 2002

IMI ADAPTIVE METHODS Wavelet Methods (WAM) : approximates u by a linear combination of n wavelets AFEM: approximates u by piecewise polynomial on partition generated by adaptive subdivision FOCM 2002

IMI FORM OF NONLINEAR APPROXIMATION Good Theorem: For a range of s >0, if u can be approximated with accuracy O(n-s) using full knowledge of u then numerical algorithm produces same accuracy using only information about u gained during the computation. Here n is the number of degrees of freedom Best Theorem: In addition bound the number of computations by Cn FOCM 2002

IMI AFEMs Initial partition P 0 and Galerkin soln. u 0 · General iterative step Pj Pj+1 and uj uj+1 i. Examine residual (a posteriori error estimators) to determine cells to be subdivided (marked cells) ii. Subdivide marked cells - results in hanging nodes. iii. Remove hanging nodes by further subdivision (completion) resulting in Pj+1 · FOCM 2002

FIRST FUNDAMENTAL THEOREMS IMI Doerfler, Morin-Nochetto-Siebert: Introduce strategy for marking cells: a posterio estimators plus bulk chasing Rule for subdivision: newest vertex bisection . . THEOREM (D, MNS): For Poisson problem algorithm convergence ) . . ) · FOCM 2002

IMI BINEV-DAHMEN-DEVORE New AFEM Algorithm: 1. Add coarsening step 2. Fundamental analysis of completion 3. Utilize principles of nonlinear approximation FOCM 2002

IMI BINEV-DAHMEN-DEVORE . . ) THEOREM (BDD): Poisson problem, for a certain range of s >0. If u can be approximated with order O(n-s ) in energy norm using full knowledge of u, then BDD adaptive algorithm does the same. Moreover, the number of computations is of order O(n). FOCM 2002

IMI ADAPTIVE WAVELET METHODS General elliptic problem u=f Problem in wavelet coordinates A u= f A: l 2 FOCM 2002 ||Av|| ~ ||v||

IMI FORM OF WAVELET METHODS · Choose a set of wavelet indices · Find Gakerkin solution u from span{ } · Check residual and update FOCM 2002

IMI COHEN-DAHMEN-DEVORE FIRST VIEW For finite index set A u = f u Galerkin sol. Generate sets j , j = 0, 1, 2, … Form of algorithm: 1. Bulk chase on residual several iterations · j~ · 2. Coarsen: j~ j+1 · 3. Stop when residual error small enough FOCM 2002

IMI · ADAPTIVE WAVELETS: COHEN-DAHMEN-DEVORE THEOREM (CDD): For SPD problems. If u can be approximated with O(n-s ) using full knowledge of u (best n term approximation), then CDD algorithm does same. Moreover, the number of computations is O(n). FOCM 2002

IMI CDD: SECOND VIEW u n+1 = u n - (A u n -f ) This infinite dimensional iterative process converges Find fast and efficient methods to compute Au n , f when u n is finitely supported. Compression of matrix vector multiplication Au n FOCM 2002

IMI · SECOND VIEW GENERALIZES Wide range of semi-elliptic, and nonlinear THEOREM (CDD): For wide range of linear and nonlinear elliptic problems. If u can be approximated with O(n-s ) using full knowledge of u (best n term approximation), then CDD algorithm does same. Moreover, the number of computations is O(n). FOCM 2002

IMI · · · WHAT WE LEARNED Proper coarsening controls size of problem Remain with infinite dimensional problem as long as possible Adaptivity is a natural stabilizer, e. g. LBB conditions for saddle point problems are not necessary FOCM 2002

IMI WHAT focm CAN DO FOR YOU · Clearly frame the computational problem · Give benchmark of optimal performance · Discretization/Analysis/Solution interplay · Identify computational issues not apparent in computational heuristics · Guide the development of optimal algorithms FOCM 2002