ИМ Ы. К ГИО Г И З О Л А. СИ БР И Я ГЕО Л О Г Л А АВТ Т Л Л П А Р А Д О К С Ы .
ЧТО ТАКОЕ ТАВТОЛОГИЯ? Это тождественно-истинная формула, которая при любых возможных истинностных значениях, входящих в них простых компонентов (переменных) истинна, то есть общезначима независимо от того, какие значения принимают входящие в неё переменные, обозначенные буквами.
ПРИМЕРЫ ТАВТОЛОГИИ А А (А) ( Р (Р)) А (В А) А А (из А следует А) (закон исключенного третьего) (закон противоречия) (истина следует из чего угодно) (закон двойного отрицания)
КАК ОПРЕДЕЛИТЬ ЯВЛЯЕТСЯ ЛИ ФОРМУЛА ТАВТОЛОГИЕЙ? Составить таблицу истинности для всевозможных комбинаций по исследуемой формуле. Если при составлении таблицы истинности мы получили противоречие, то формула не является тавтологией.
ЧТО ТАКОЕ СИЛЛОГИЗМ? Это логическое рассуждение, состоящее из двух посылок, связанных друг с другом общим (средним) термином, и следующего из посылок заключения. В силлогизме обязательно присутствуют 3 термина: один средний и два крайних. Заключение определяет связь крайних терминов друг с другом.
ПРИМЕР СИЛЛОГИЗМА Пример правильно силлогизма: «Все ноутбуки – компьютеры. Все компьютеры имеют процессор. Следовательно, все ноутбуки имеют процессор» . Пример неправильного силлогизма: «Все компьютеры являются электрическими приборами. Некоторые электрические приборы являются утюгами. Значит – некоторые компьютеры являются утюгами» . Доказано, что общее число силлогизмов, которые можно составить из суждений указанного вида, равно 256, из них правильных всего 24.
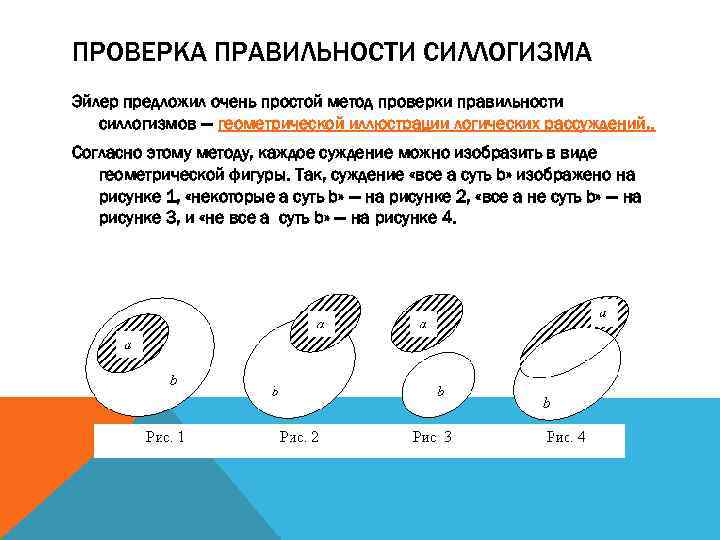ПРОВЕРКА ПРАВИЛЬНОСТИ СИЛЛОГИЗМА Эйлер предложил очень простой метод проверки правильности силлогизмов — геометрической иллюстрации логических рассуждений, . Согласно этому методу, каждое суждение можно изобразить в виде геометрической фигуры. Так, суждение «все a суть b» изображено на рисунке 1, «некоторые a суть b» — на рисунке 2, «все a не суть b» — на рисунке 3, и «не все a суть b» — на рисунке 4.
ЧТО ТАКОЕ ПАРАДОКС Это ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения.
ПРИМЕРЫ МАТЕМАТИЧЕСКИХ ПАРАДОКСОВ Феномен Уилла Роджерса — кажущийся парадокс, заключающийся в том, что перемещение (численного) элемента из одного множества в другое может увеличить среднее значение обоих множеств. Рассмотрим два множества, A и B: A = {1, 2, 3, 4}, B = {5, 6, 7, 8, 9}. Арифметическое среднее элементов A равно 2, 5, элементов B — 7. Однако, если число 5 переместить из B в A, получив A = {1, 2, 3, 4, 5}, B = {6, 7, 8, 9}, то среднее значение элементов A повысится до 3, а среднее значение элементов B — до 7, 5.