 II признак равенства треугольников по стороне и двум прилежащим к ней углам. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. В 1 В А 1 А ЗАКЛЮЧЕНИЕ У С Л О В И Е С С 1
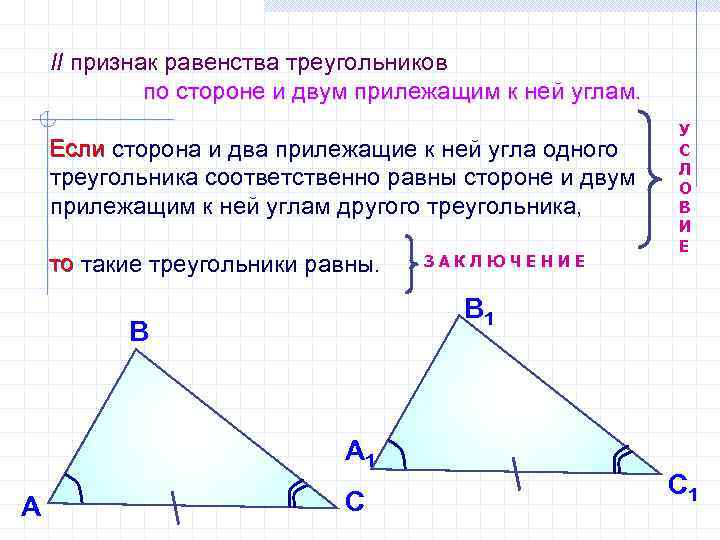
II признак равенства треугольников по стороне и двум прилежащим к ней углам. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. В 1 В А 1 А ЗАКЛЮЧЕНИЕ У С Л О В И Е С С 1
 Дано: АВС, А 1 В 1 С 1, АВ = А 1 В 1 А = А 1 Доказать: АВС = А 1 В 1 С 1, В= В 1 С 1 Используем способ наложения. С Так как стороны АВ и А 1 В 1 равны, то совпадут точки А 1; В и В 1. Так как равны углы А и А 1, то совпадут лучи АС и А 1 С 1. А 1 А Так как равны углы В и В 1, то совпадут лучи ВС и В 1 С 1. В Треугольники АВС и А 1 В 1 С 1 совместятся, значит, они равны. В 1
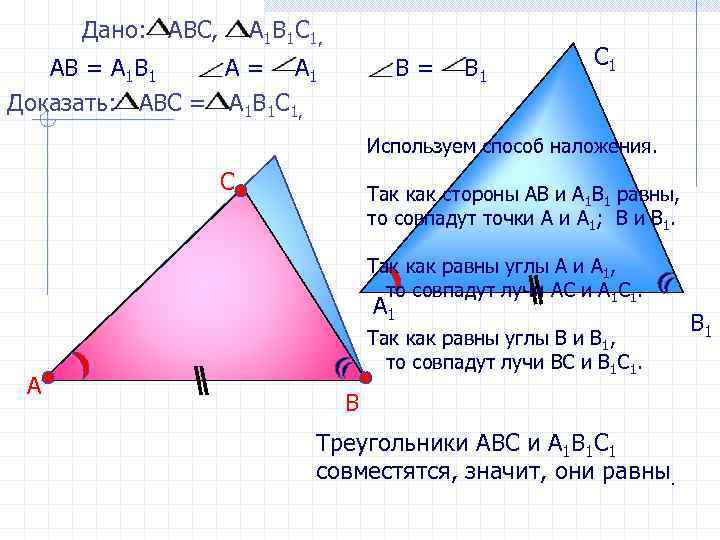
Дано: АВС, А 1 В 1 С 1, АВ = А 1 В 1 А = А 1 Доказать: АВС = А 1 В 1 С 1, В= В 1 С 1 Используем способ наложения. С Так как стороны АВ и А 1 В 1 равны, то совпадут точки А 1; В и В 1. Так как равны углы А и А 1, то совпадут лучи АС и А 1 С 1. А 1 А Так как равны углы В и В 1, то совпадут лучи ВС и В 1 С 1. В Треугольники АВС и А 1 В 1 С 1 совместятся, значит, они равны. В 1
 Для красного треугольника найдите равный и щёлкните по нему мышкой. C K см 3 2 840 540 23 см 840 540 M B А E N Z D 540 840 23 см I Не 0 верно! 54 23 см O Проверка S
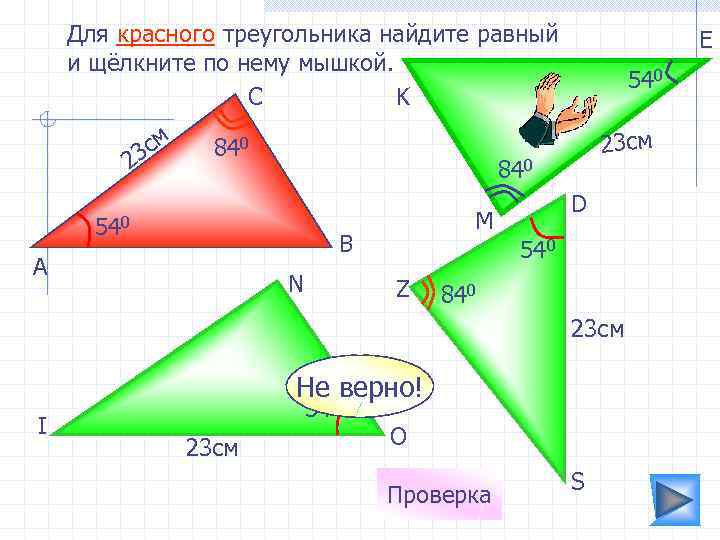
Для красного треугольника найдите равный и щёлкните по нему мышкой. C K см 3 2 840 540 23 см 840 540 M B А E N Z D 540 840 23 см I Не 0 верно! 54 23 см O Проверка S
 Доказать: АВС = СDO С В D А
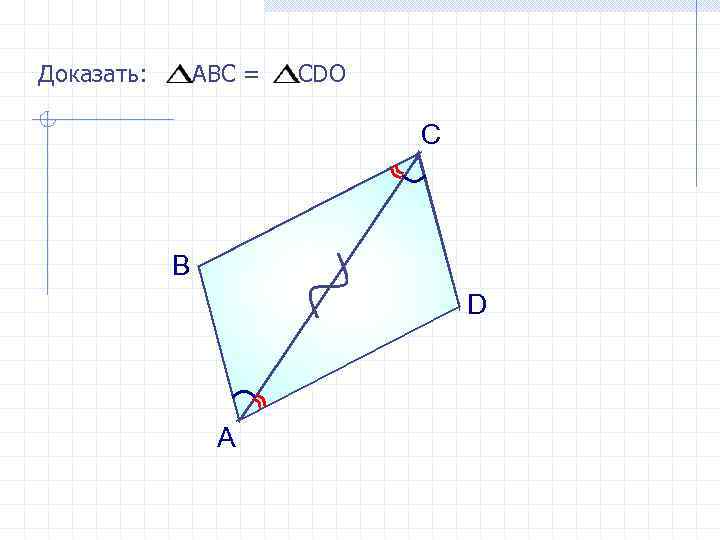
Доказать: АВС = СDO С В D А
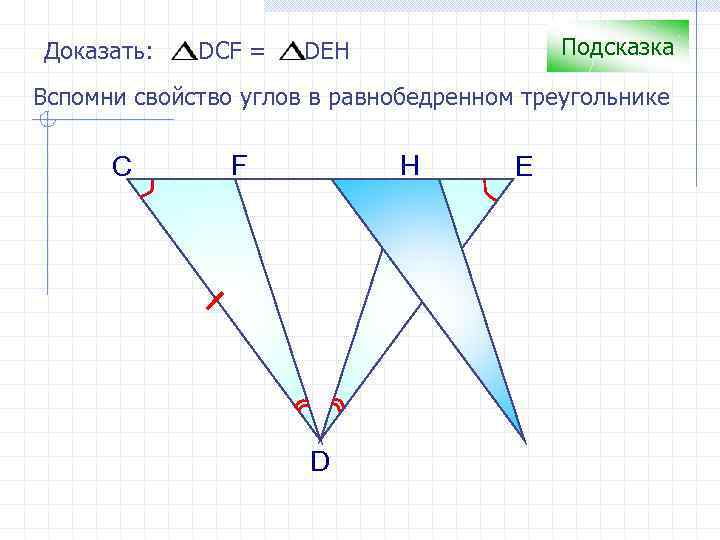 Доказать: DCF = Подсказка DEH Вспомни свойство углов в равнобедренном треугольнике С F H D E
Доказать: DCF = Подсказка DEH Вспомни свойство углов в равнобедренном треугольнике С F H D E
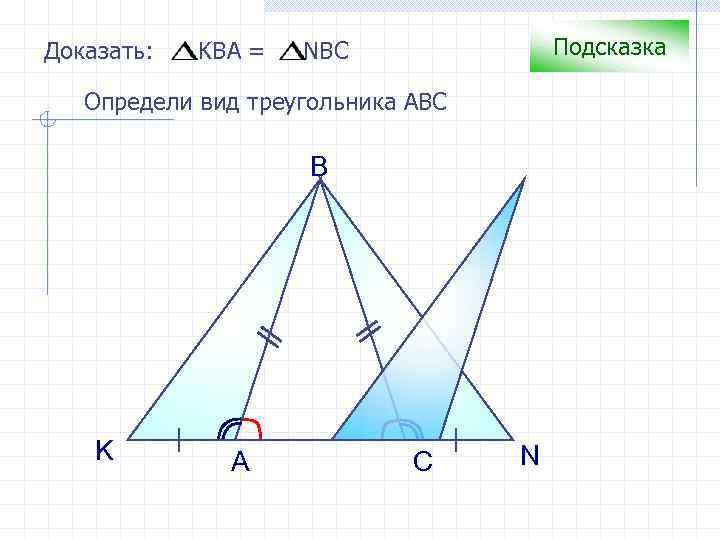 Доказать: KBA = Подсказка NBC Определи вид треугольника АВС B K A C N
Доказать: KBA = Подсказка NBC Определи вид треугольника АВС B K A C N
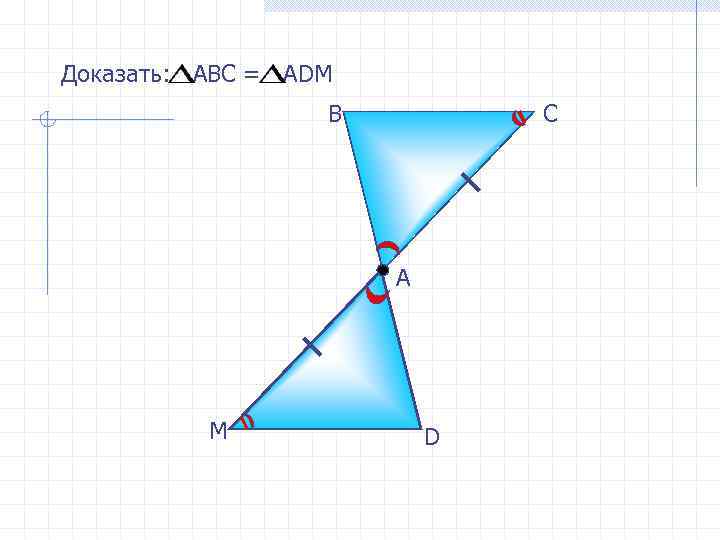 Доказать: АВС = АDМ В С А М D
Доказать: АВС = АDМ В С А М D
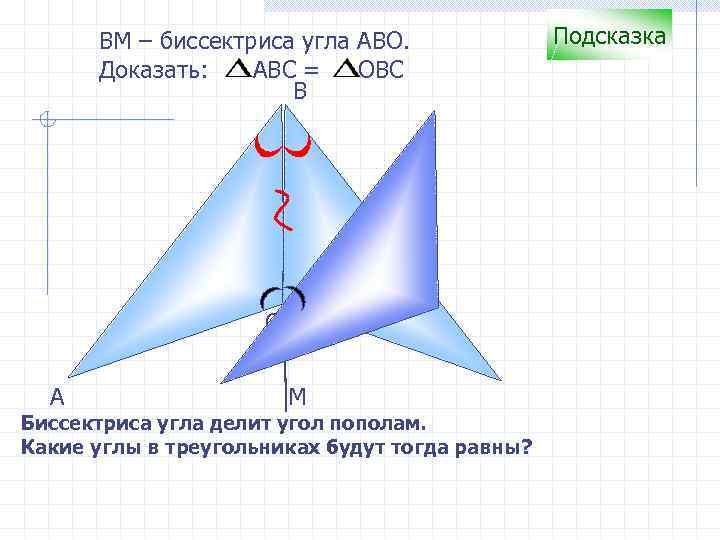 ВM – биссектриса угла АВО. Доказать: АВС = ОВС B С А М Биссектриса угла делит угол пополам. Какие углы в треугольниках будут тогда равны? Подсказка
ВM – биссектриса угла АВО. Доказать: АВС = ОВС B С А М Биссектриса угла делит угол пополам. Какие углы в треугольниках будут тогда равны? Подсказка
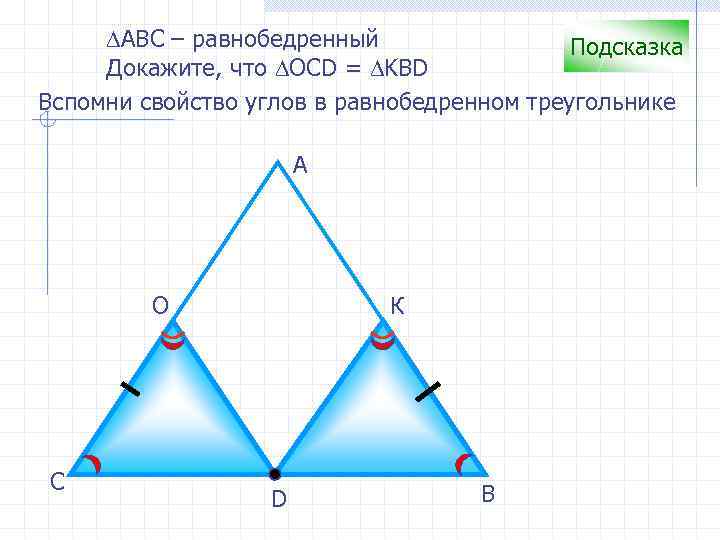 ∆АВС – равнобедренный Подсказка Докажите, что ∆OCD = ∆KBD Вспомни свойство углов в равнобедренном треугольнике А О С К D В
∆АВС – равнобедренный Подсказка Докажите, что ∆OCD = ∆KBD Вспомни свойство углов в равнобедренном треугольнике А О С К D В
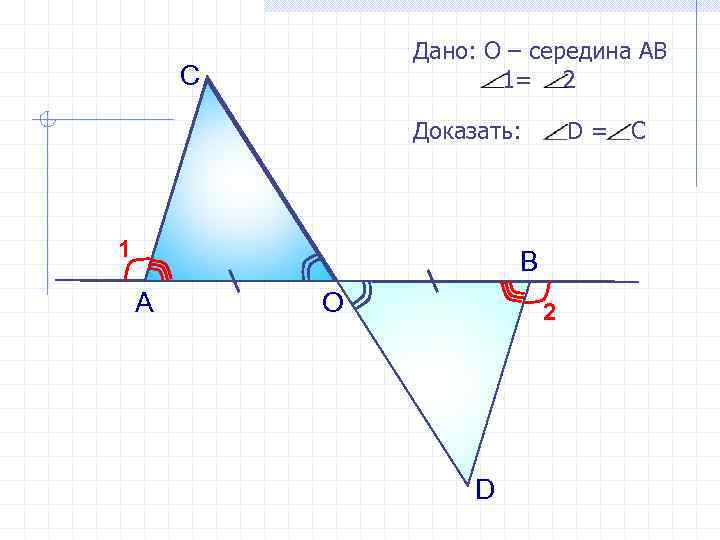 Дано: О – середина АВ 1= 2 С Доказать: 1 D= C В А О 2 D
Дано: О – середина АВ 1= 2 С Доказать: 1 D= C В А О 2 D
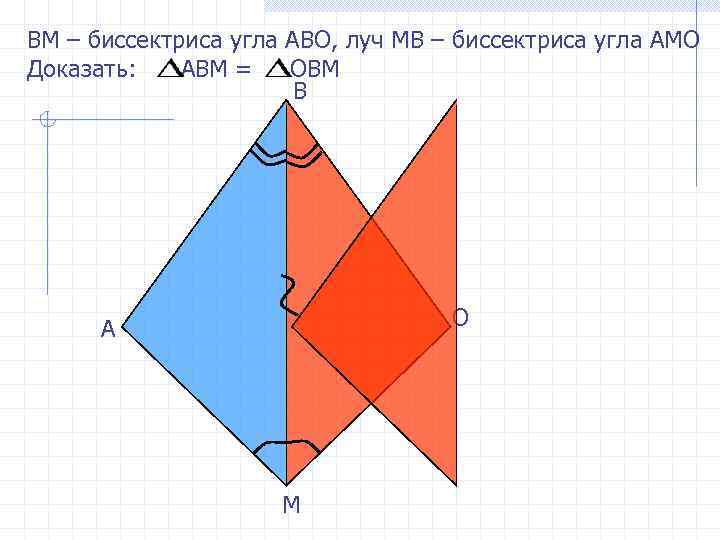 ВM – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ B О А М
ВM – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ B О А М
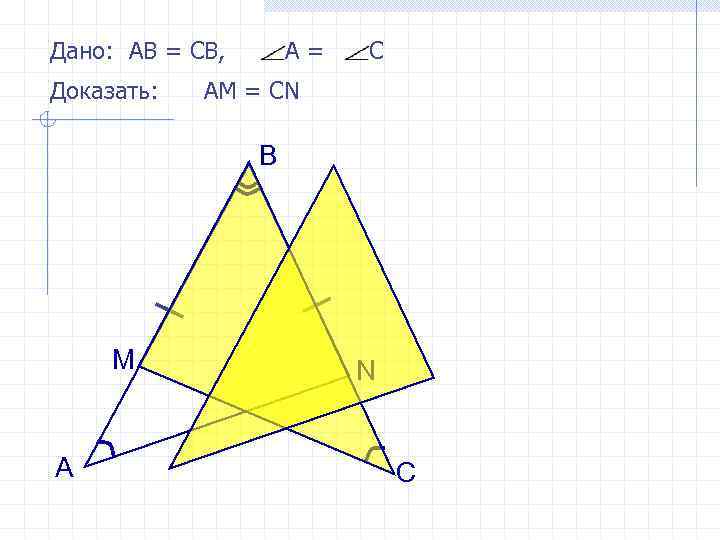 Дано: АВ = СВ, Доказать: А= С АМ = СN B M А N C
Дано: АВ = СВ, Доказать: А= С АМ = СN B M А N C
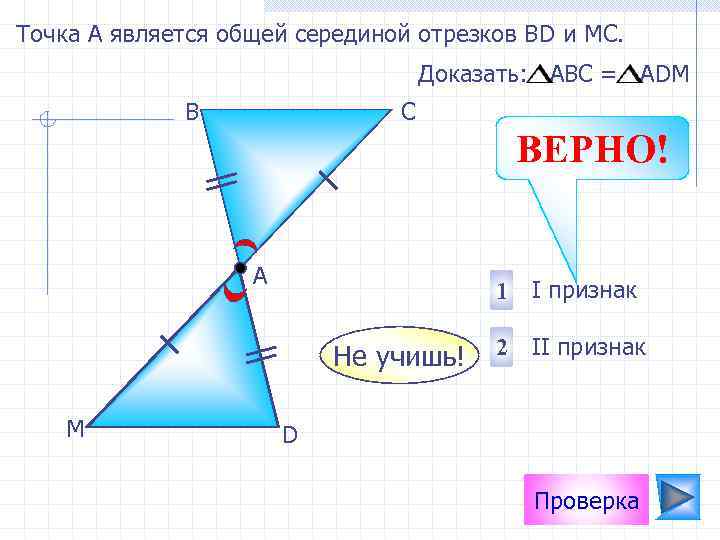 Точка А является общей серединой отрезков ВD и МС. Доказать: АВС = АDМ В С ВЕРНО! А 1 I признак Не учишь! М 2 II признак D Проверка
Точка А является общей серединой отрезков ВD и МС. Доказать: АВС = АDМ В С ВЕРНО! А 1 I признак Не учишь! М 2 II признак D Проверка
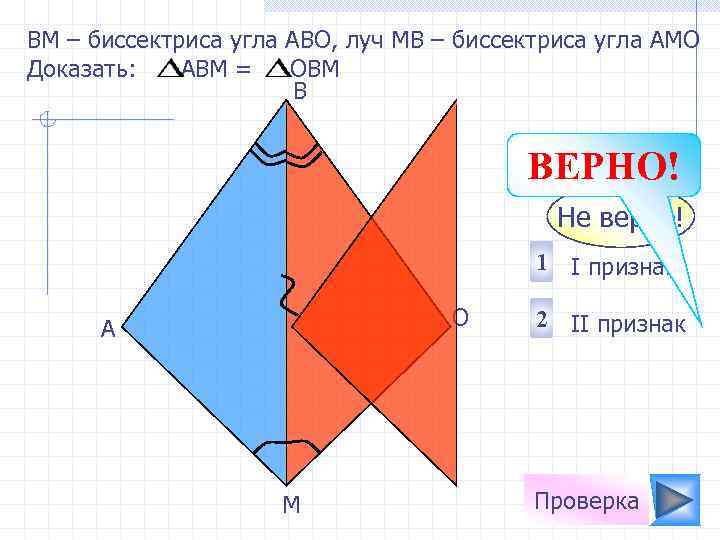 ВM – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ B ВЕРНО! Не верно! 1 I признак О А М 2 II признак Проверка
ВM – биссектриса угла АВО, луч МВ – биссектриса угла АМО Доказать: АВМ = ОВМ B ВЕРНО! Не верно! 1 I признак О А М 2 II признак Проверка
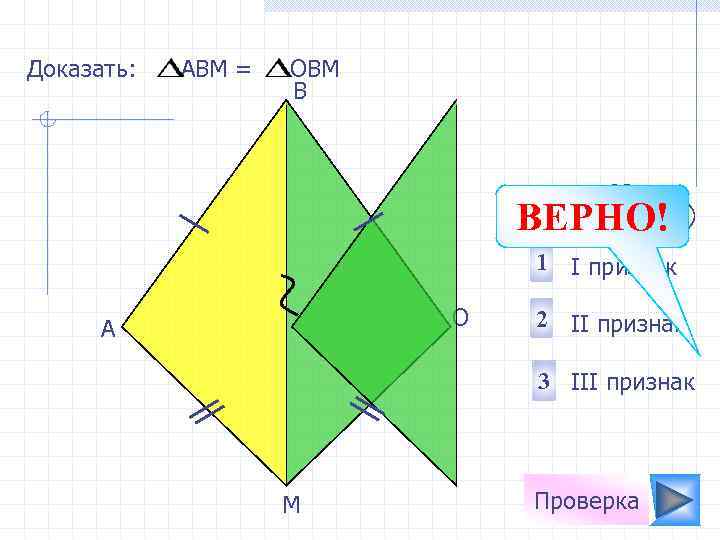 Доказать: АВМ = ОВМ B Не верно! ВЕРНО! 1 I признак О А 2 II признак 3 III признак М Проверка
Доказать: АВМ = ОВМ B Не верно! ВЕРНО! 1 I признак О А 2 II признак 3 III признак М Проверка
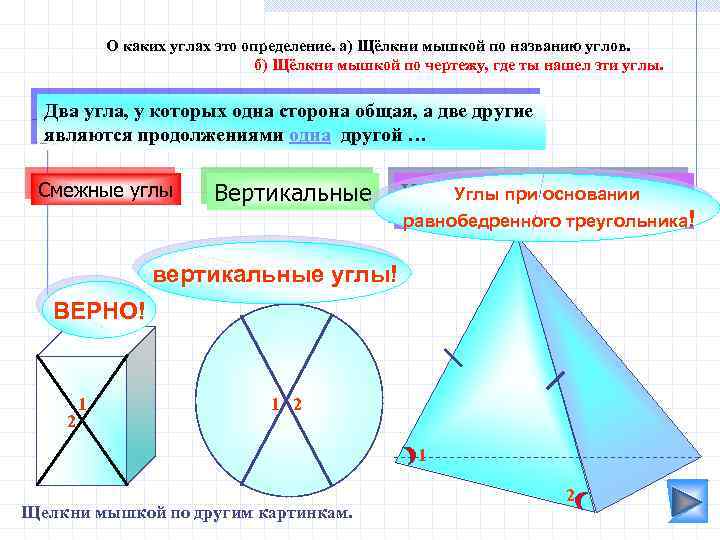 О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой … Смежные углы Вертикальные Углыосновании при основании равнобедренного треугольника ! равнобедренного треугольника вертикальные углы! ВЕРНО! 2 1 1 2 1 Щелкни мышкой по другим картинкам. 2
О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой … Смежные углы Вертикальные Углыосновании при основании равнобедренного треугольника ! равнобедренного треугольника вертикальные углы! ВЕРНО! 2 1 1 2 1 Щелкни мышкой по другим картинкам. 2
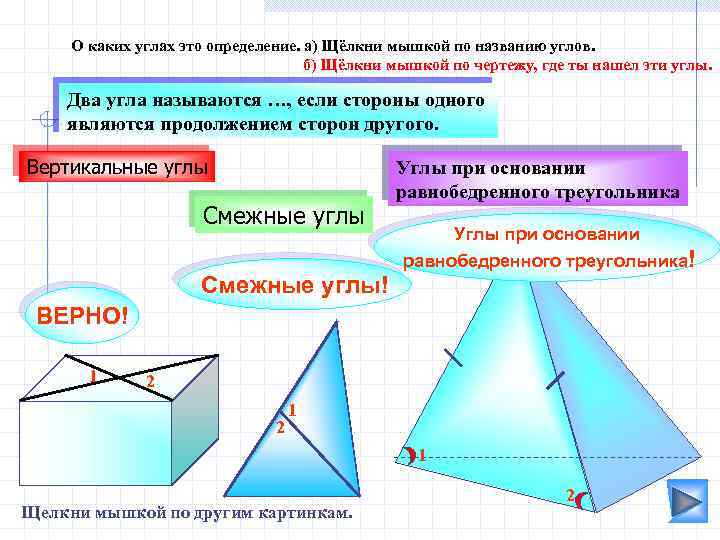 О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. Два угла называются …, если стороны одного являются продолжением сторон другого. Вертикальные углы Смежные углы! Углы при основании равнобедренного треугольника! ВЕРНО! 1 2 2 1 1 Щелкни мышкой по другим картинкам. 2
О каких углах это определение. а) Щёлкни мышкой по названию углов. б) Щёлкни мышкой по чертежу, где ты нашел эти углы. Два угла называются …, если стороны одного являются продолжением сторон другого. Вертикальные углы Смежные углы! Углы при основании равнобедренного треугольника! ВЕРНО! 1 2 2 1 1 Щелкни мышкой по другим картинкам. 2