Игры в смешанных стратегиях Моделирование конфликтных

Игры в смешанных стратегиях

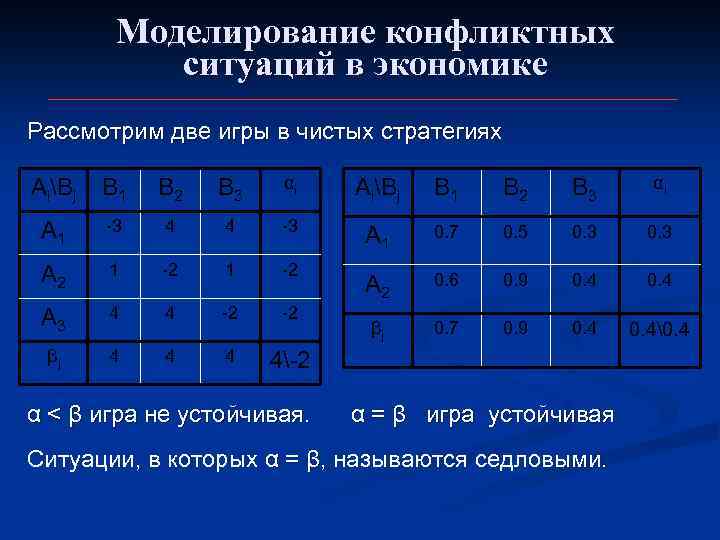Моделирование конфликтных ситуаций в экономике Рассмотрим две игры в чистых стратегиях AiBj B 1 B 2 B 3 αi AiBj B 1 B 2 B 3 αi A 1 -3 4 4 -3 0. 7 0. 5 0. 3 A 1 A 2 1 -2 1 -2 A 2 0. 6 0. 9 0. 4 A 3 4 4 -2 βj 0. 7 0. 9 0. 4. 4 βj 4 4-2 α < β игра не устойчивая. α = β игра устойчивая Ситуации, в которых α = β, называются седловыми.

Моделирование конфликтных ситуаций в экономике Седловых ситуаций (точек) в матрице игры может быть несколько. Например: B 1 B 2 B 3 B 4 B 5 B 6 αi Здесь α=β=2 A 1 2 3 2 6 2 4 2 Оптимальные стратегии игроков: A 2 1 2 0 0 1 1 0 А 1 и А 3; В 1, В 3 и В 5 A 3 2 6 2 3 2 7 2 A 4 0 5 1 7 1 4 0 βj 2 6 2 7 22 Вопрос. Как построить игру, чтобы выигрыш был больше α, а проигрыш меньше β.

Моделирование конфликтных ситуаций в экономике 1. Игры в смешанных стратегиях. Имеем SAc={A 1, A 2, …, Am}, Sc. B={B 1, B 2, …, Bn}, FA(x), FB(y) Определение. Смешанной называется стратегия игрока, состоящая в случайном чередовании одной из своих чистых стратегий. Смешанная стратегия – дискретная случайная величина, значениями которой являются номера чистых стратегий. Т. е. каждой чистой стратегии ставится в соответствие вероятность ее появления в игре.

Моделирование конфликтных ситуаций в экономике 1. Игры в смешанных стратегиях. Имеем: SAc={A 1, A 2, …, Am}, Р={p 1, p 2, …, pm}, Σpi = 1 Sc. B={B 1, B 2, …, Bn} Q={q 1, q 2, …, qn}, Σqi = 1 P и Q будем называть смешанными стратегиями игроков А и В. Определение. Множество SA={P(p 1, p 2, …, pm), Σpi = 1} называется множеством смешанных стратегий игрока А.

Моделирование конфликтных ситуаций в экономике 1. Игры в смешанных стратегиях. Свойства множества смешанных стратегий: - SA={P(p 1, p 2, …, pm), Σpi = 1} – бесконечно, - множество SA={P(p 1, p 2, …, pm), Σpi = 1} содержит множество SAc={A 1, A 2, …, Am} как частный случай: А 1 = {1, 0, 0, …, 0}, A 2={0, 1, 0, …, 0}, A 3={0, 0, 1, 0, …, 0} Для смешанной стратегии справедливо равенство: P = p 1 A 1+p 2 A 2+…+pm. Am = =p 1(1, 0, …, 0)+p 2(0, 1, 0…, 0)+…+pm(0, 0, …, 1) = Σpi Ai

Моделирование конфликтных ситуаций в экономике 1. Игры в смешанных стратегиях. Игра протекает следующим образом: Если игрок А придерживается одной из своих смешанных стратегий, то для определения конкретной чистой стратегии в партии, вначале запускается генератор случайных чисел и в соответствии с полученным числом делается ход. Например. Стратегия игрока А - P = {1/6, 3/6, 2/6}. 1. Бросается «кубик» с гранями {1, 2, 2, 2, 3, 3}. 2. Если выпал « 2» , делается ход А 2.

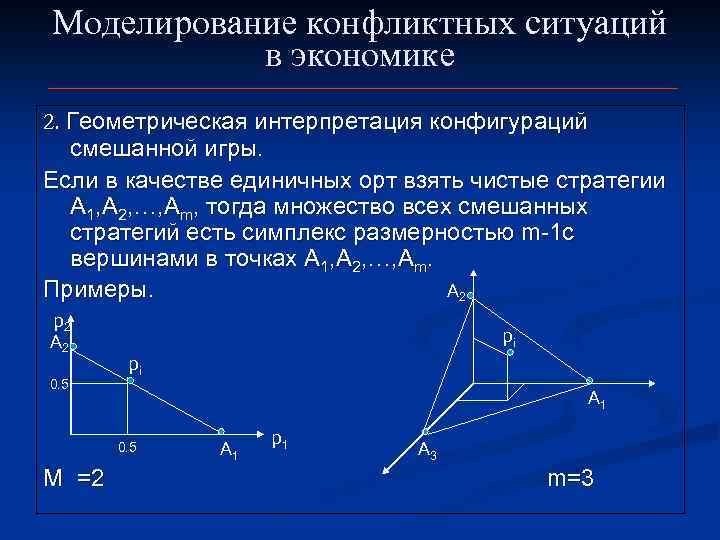Моделирование конфликтных ситуаций в экономике 2. Геометрическая интерпретация конфигураций смешанной игры. Если в качестве единичных орт взять чистые стратегии А 1, A 2, …, Аm, тогда множество всех смешанных стратегий есть симплекс размерностью m-1 с вершинами в точках А 1, A 2, …, Аm. Примеры. A 2 p 2 A 2 pi 0. 5 A 1 0. 5 p 1 A 3 M =2 m=3

Моделирование конфликтных ситуаций в экономике 3. Функция выигрыша в смешанных стратегиях. Игра в смешанных стратегиях есть расширение игры с множества чистых стратегий на множество смешанных стратегий. Состояние (PQ) в игре называется ситуацией в смешанных стратегиях. Вероятность появления в игре ситуации (Ai. Bj) равна произведению piqj. Следовательно, (piqj) есть вероятность получения игроком А выигрыша F(Ai. Bj)=aij. Таким образом, вероятность появления выигрыша aij есть дискретная случайная величина. Тогда средний выигрыш в игре есть математическое ожидание случайной величины aij : M(x) = ΣΣpiaijqj

Моделирование конфликтных ситуаций в экономике 3. Функция выигрыша в смешанных стратегиях Определение. Функция H(P, Q), заданная на множестве смешанных стратегий SA×SB игроков А и В в ситуации (P, Q) называется функцией выигрыша игрока А, если ее значение равно среднему выигрышу в этой ситуации: H(P, Q) = ΣΣpiaijqj, PQ є SA×SB (2. 1) или матричной форме: H(P, Q) = PAQT (2. 2) Совокупность {SA, SB, H} множеств смешанных стратегий игроков А и В и функции выигрыша игрока А в смешанных стратегиях называют смешанным расширением игры {SAc, SBc, FA}

Моделирование конфликтных ситуаций в экономике 3. Функция выигрыша в смешанных стратегиях. Задача. Дана платежная матрица игры 2× 3 и две смешанные стратегии игроков P 0={3/8, 5/8}, Q 0={1/4, 0, 3/4} A i B j B 1 B 2 B 3 A 1 0 ½ 5/6 A 2 1 ¾ ½ Определить выигрыш игрока А в ситуациях: (P 0 Q 0), (P 0 B 1), (P 0 B 2), (P 0 B 3)

Моделирование конфликтных ситуаций в экономике Задача. Решение Аналогично можно вычислить выигрыш игроков в различных ситуациях

Моделирование конфликтных ситуаций в экономике 4. Основные определения и теоремы. Теорема 1. Для каждой смешанной стратегии Р игрока А существует α(Р, SB) = min H(PQ), a для каждой смешанной стратегии Q игрока В существует β(Q, SA) = max Н(PQ) Определение. Число α(Р, SB) называется показателем эффективности смешанной стратегии Р игрока А относительно множества смешанных стратегий игрока В. Если заменить SB на SBс, то получим определение показателя эффективности смешанной стратегии Р игрока А относительно множества чистых стратегий игрока В. Если Р есть Аi, то α(Р, SBс) =min H(PQ) = αi

Моделирование конфликтных ситуаций в экономике 4. Основные определения и теоремы. Теорема 2. Показатели эффективности любой смешанной стратегии Р игрока А относительно множеств SBс и SB равны между собой α(Р, SB) = α(Р, SBс). Расширение множества чистых стратегий игрока В не изменяет показателя эффективности игрока А.

Моделирование конфликтных ситуаций в экономике 4. Основные определения и теоремы. Определение. Число β(Р, SА) называется показателем неэффективности смешанной стратегии Q игрока B относительно множества смешанных стратегий игрока A. Если заменить SA на SAс, то получим определение показателя неэффективности смешанной стратегии Q игрока B относительно множества чистых стратегий игрока A. Если Q есть Bj, то β(Q, SAс) =max H(PQ) = βj Справедлива теорема β(Q, SAс) = β(Q, SA)

Моделирование конфликтных ситуаций в экономике 4. Основные определения и теоремы. Определение. Нижней ценой (максимином) матричной игры в смешанных стратегиях называется величина = max α(P) = max min. H(PQ) Верхней ценой (минимаксом) матричной игры в смешанных стратегиях называется величина = min β(Q) = min max H(PQ) Теорема. Для любой конечной матричной игры существуют нижняя и верхняя границы игры в смешанных стратегиях, т. е. для любой матрицы игры А существует смешанная стратегия Р 0, для которой V=max α(P)= α(P 0) и существует Q 0, для которой V=minβ(Q)= β(Q 0) Частный случай: Р 0=Аi, Q 0=Bi и равны соответственно максимину и минимаксу игры в чистых стратегиях

Моделирование конфликтных ситуаций в экономике 4. Основные определения и теоремы. Теорема. Нижняя цена игры α и верхняя цена игры β в чистых и нижняя V и верхняя V цены игры в смешанных стратегиях удовлетворяют следующему неравенству: α≤V≤V≤β. Это означает, что в любой ситуации в смешанных стратегиях (PQ) выигрыш H(PQ) не ниже показателя эффективности α(P) его стратегий

Моделирование конфликтных ситуаций в экономике 5. Решение игры в смешанных стратегиях Определение. Если нижняя V и верхняя V цены игры в смешанных стратегиях равны , то их общее значение V называется ценой игры в смешанных стратегиях, а стратегии P 0 и Q 0, для которых выполняется равенство V = α(P 0) =β(Q 0) = H(P 0 Q 0) называются оптимальными смешанными стратегиями соответственно игроков А и В. Оптимальные смешанные стратегии игроков обладают тем свойством, что, если один из игроков придерживается своей оптимальной стратегии, то противнику не выгодно отклоняться от своей оптимальной стратегии. Цена игры в смешанных стратегиях: α≤V≤β

Моделирование конфликтных ситуаций в экономике 5. Решение игры в смешанных стратегиях. Определение. Полным решением игры в смешанных стратегиях называется совокупность {SA 0, SB 0, V} множеств оптимальных стратегий игроков и цены игры. Определение. Любая пара оптимальных стратегий (P 0, Q 0) образуют частное решение игры в смешанных стратегиях. Теорема фон Неймана. Любая матричная игра имеет решение в смешанных стратегиях, т. е. существуют оптимальные стратегии игроков P 0, Q 0 и цена игры V. Точка H(P 0, Q 0) называется седловой точкой матрицы игры в смешанных стратегиях.