Игры с природой При принятии управленческих решений

Игры с природой

При принятии управленческих решений в условиях неопределённости противником игрока (лица, принимающего решения – ЛПР) является некоторая объективная действительность, которую принято называть природой. Игра с природой (статистическая игра) – это парная матричная игра, в которой сознательный игрок А (статистик) выступает против участника, совершенно безразличного к результату игры, называемого природой.

Для описания игры используется платёжная матрица игры, где строки это стратегии А 1, А 2, …, Аm игрока-статистика А, а возможные состояния среды (столбцы платёжной матрицы), в которой реализуются эти стратегии есть В 1, В 2, …, Вn. Величина аij (i=1, 2, …, m; j=1, 2, …, n) есть выигрыш(потеря) игрока А при реализации стратегии Аi в среде, находящейся в состоянии Вj. В играх с природой исключать можно только доминируемые стратегии игрока А. Столбцы, отвечающие стратегиям природы, нельзя вычеркивать из матрицы игры

Возможен и другой способ задания матрицы игры с природой не в виде матрицы выигрышей (потерь), а в виде так называемой матрицы рисков R. Величина риска – это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей (потерь) А.

Матрица рисков позволяет количественно оценить эффективность различных стратегий Аi в зависимости от состояний среды Вj. Риск– это разность между результатом, который игрок мог бы получить, если бы он знал действительное состоянием среды, и результатом, который игрок получит при j-й стратегии.

Зная состояние природы (стратегию) , игрок выбирает ту стратегию, при которой его выигрыш максимальный или потеря минимальна, то есть элементы матрицы рисков связаны с элементами матрицы выигрышей (потерь) следующими соотношениями:

Критерии принятия решений в играх с природой.

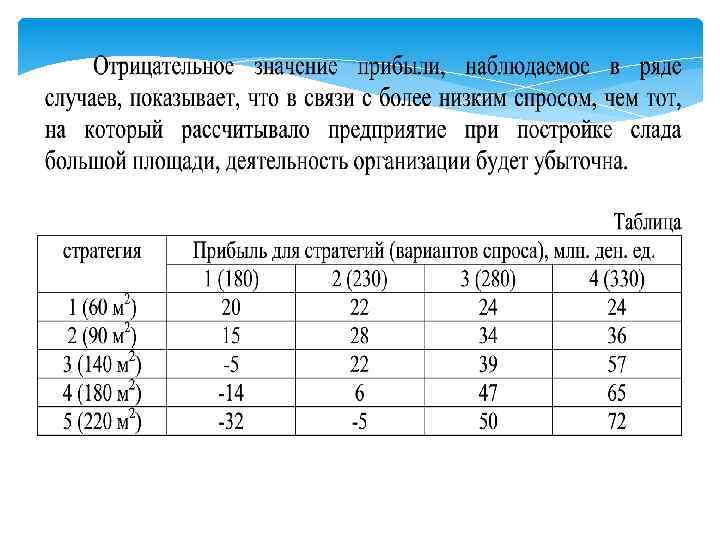
2. Критерий Сэвиджа. Построим матрицу рисков, воспользовавшись исходной матрицей и соотношением, принятым для матрицы выигрышей: Где: - максимальный элемент в столбце матрицы.

Критерий минимаксного риска Севиджа: S=min max (48, 36, 25, 34, 52) По критерию Севиджа наилучшей стратегией является стратегия А 3, то есть строительство склада площадью 140 м 2. 3. Критерий Гурвица. Допустим, что уменьшение и увеличение запасов равновероятно и коэффициент пессимизма-оптимизма Так как в данной задаче рассматривается матрица выигрышей, то применяется критерий

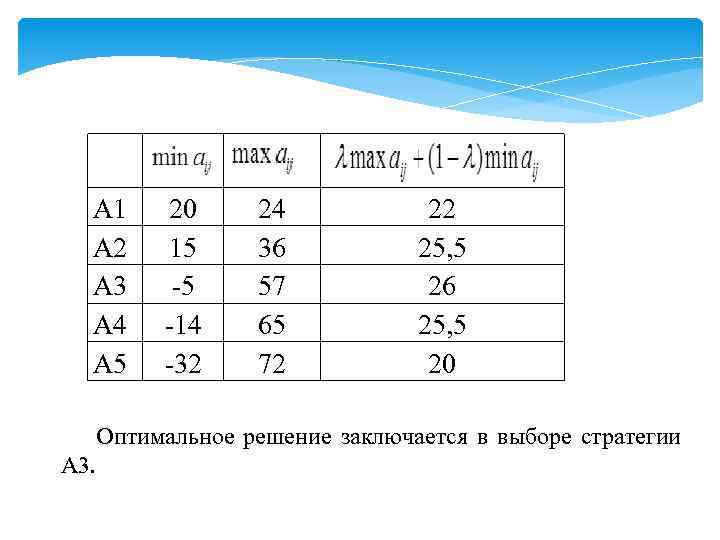А 1 А 2 А 3 А 4 А 5 20 15 -5 -14 -32 24 36 57 65 72 22 25, 5 26 25, 5 20 Оптимальное решение заключается в выборе стратегии А 3.

Рассчитаем оптимальную стратегию применительно к матрице рисков: А 1 А 2 А 3 А 4 А 5 0 0 6 3 0 48 36 25 34 52 24 18 15, 5 18, 5 26

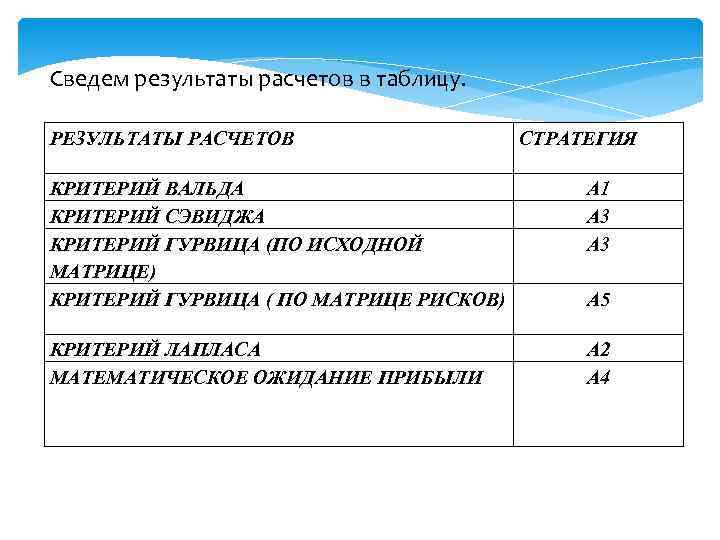Сведем результаты расчетов в таблицу. РЕЗУЛЬТАТЫ РАСЧЕТОВ СТРАТЕГИЯ КРИТЕРИЙ ВАЛЬДА КРИТЕРИЙ СЭВИДЖА КРИТЕРИЙ ГУРВИЦА (ПО ИСХОДНОЙ МАТРИЦЕ) КРИТЕРИЙ ГУРВИЦА ( ПО МАТРИЦЕ РИСКОВ) А 1 А 3 КРИТЕРИЙ ЛАПЛАСА МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ПРИБЫЛИ А 2 А 4 А 5

Вывод. Исходя из рассмотренных критериев и учета того, что принимается разовое ответственное решение, для рассматриваемого примера лучшим вариантом является номер 3, т. е. строительство склада площадью 140 м 2.