Игра «Total Recall» Тема 4. Портфельный

























Международный инвестиционный менеджмент_7.ppt
- Количество слайдов: 46
 Игра «Total Recall»
Игра «Total Recall»
 Тема 4. Портфельный анализ
Тема 4. Портфельный анализ
 Содержание темы 4. 1. Теорема об эффективном множестве 4. 2. Достижимое множество 4. 3. Выбор оптимального портфеля. Вогнутость эффективного множества 4. 4. Рыночная модель. Рыночный и собственный риск портфеля 4. 5. Диверсификация
Содержание темы 4. 1. Теорема об эффективном множестве 4. 2. Достижимое множество 4. 3. Выбор оптимального портфеля. Вогнутость эффективного множества 4. 4. Рыночная модель. Рыночный и собственный риск портфеля 4. 5. Диверсификация
 Теорема об эффективном множестве Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых: 1. Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска, 2. Обеспечивает минимальный риск для некоторого значения ожидаемой доходности. Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством.
Теорема об эффективном множестве Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых: 1. Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска, 2. Обеспечивает минимальный риск для некоторого значения ожидаемой доходности. Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством.
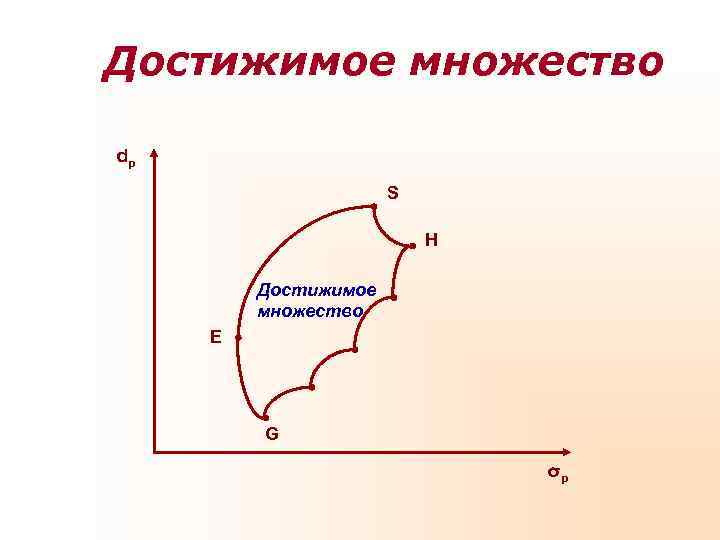
 Достижимое множество известно как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. То есть все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества.
Достижимое множество известно как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. То есть все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества.
 Достижимое множество dp S H Достижимое множество Е G σp
Достижимое множество dp S H Достижимое множество Е G σp
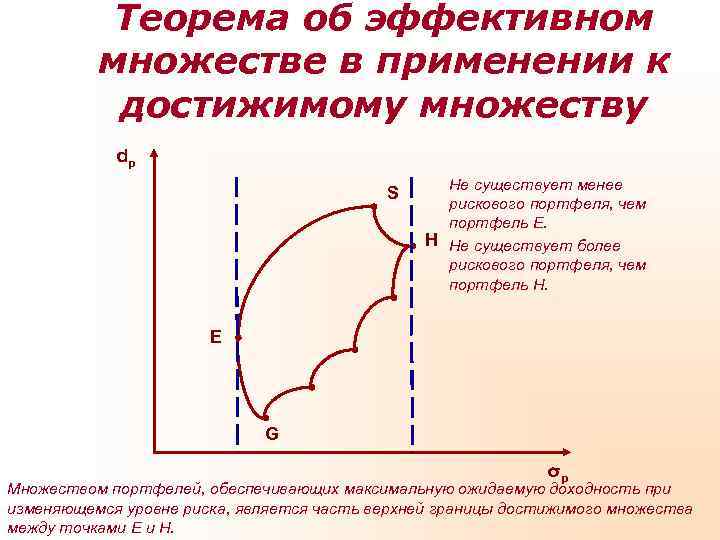
 Теорема об эффективном множестве в применении к достижимому множеству dp Не существует менее S рискового портфеля, чем портфель Е. H Не существует более рискового портфеля, чем портфель Н. Е G σp Множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества между точками Е и Н.
Теорема об эффективном множестве в применении к достижимому множеству dp Не существует менее S рискового портфеля, чем портфель Е. H Не существует более рискового портфеля, чем портфель Н. Е G σp Множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества между точками Е и Н.
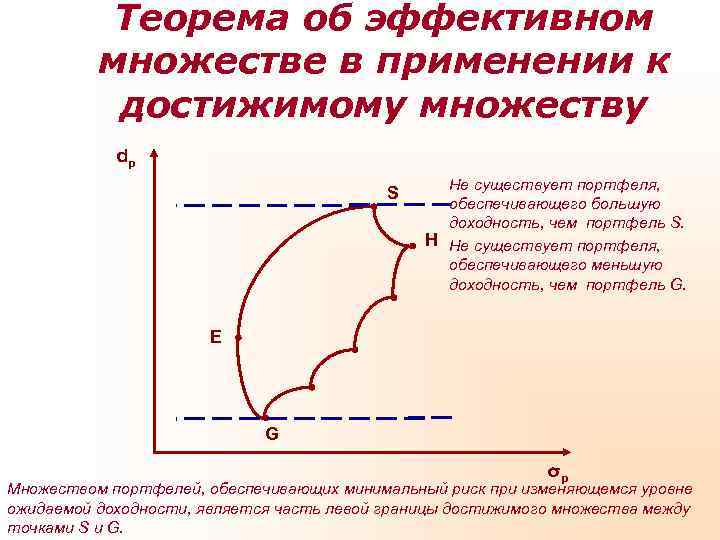
 Теорема об эффективном множестве в применении к достижимому множеству dp Не существует портфеля, S обеспечивающего большую доходность, чем портфель S. H Не существует портфеля, обеспечивающего меньшую доходность, чем портфель G. Е G σp Множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества между точками S и G.
Теорема об эффективном множестве в применении к достижимому множеству dp Не существует портфеля, S обеспечивающего большую доходность, чем портфель S. H Не существует портфеля, обеспечивающего меньшую доходность, чем портфель G. Е G σp Множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества между точками S и G.
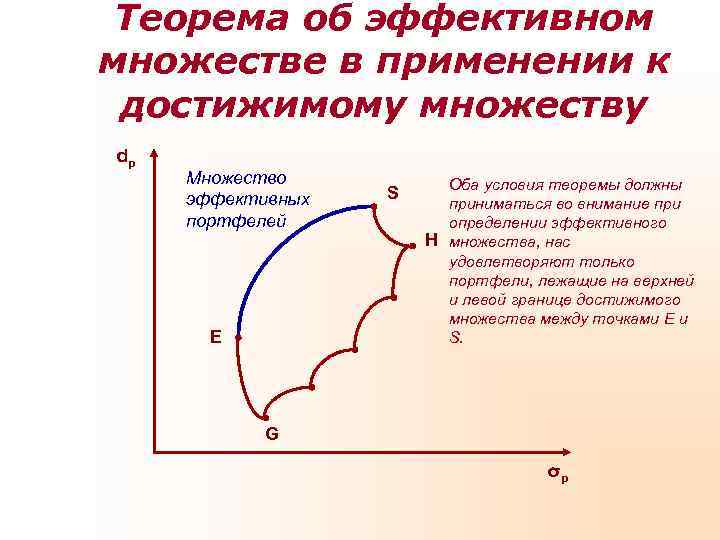
 Теорема об эффективном множестве в применении к достижимому множеству dp Множество Оба условия теоремы должны эффективных S приниматься во внимание при портфелей определении эффективного H множества, нас удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества между точками Е и Е S. G σp
Теорема об эффективном множестве в применении к достижимому множеству dp Множество Оба условия теоремы должны эффективных S приниматься во внимание при портфелей определении эффективного H множества, нас удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества между точками Е и Е S. G σp
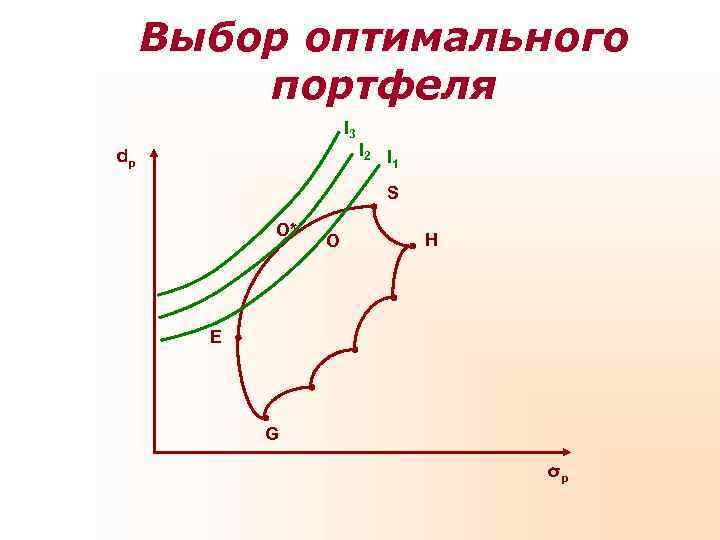
 Выбор оптимального портфеля I 3 dp I 2 I 1 S O* O H Е G σp
Выбор оптимального портфеля I 3 dp I 2 I 1 S O* O H Е G σp
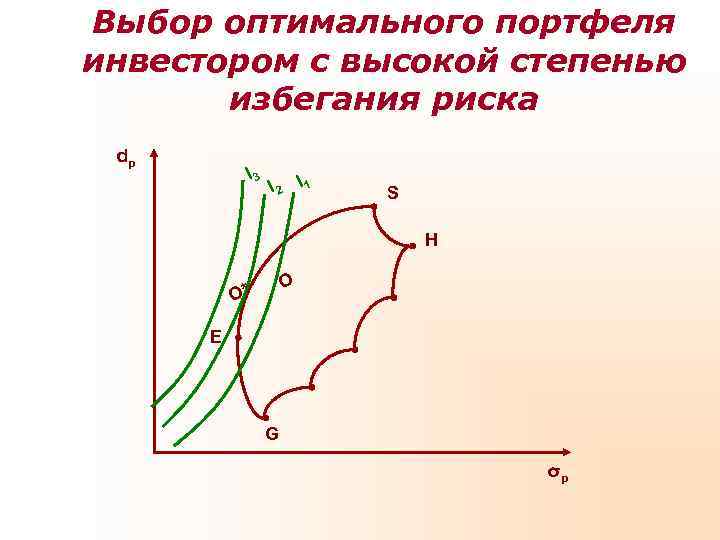
 Выбор оптимального портфеля инвестором с высокой степенью избегания риска dp I 3 I 2 I 1 S H O O* Е G σp
Выбор оптимального портфеля инвестором с высокой степенью избегания риска dp I 3 I 2 I 1 S H O O* Е G σp
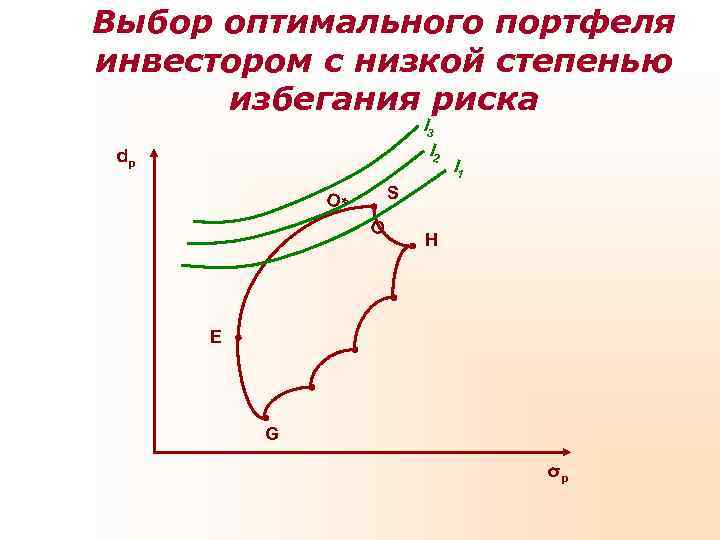
 Выбор оптимального портфеля инвестором с низкой степенью избегания риска I 3 dp I 2 I 1 O* S O H Е G σp
Выбор оптимального портфеля инвестором с низкой степенью избегания риска I 3 dp I 2 I 1 O* S O H Е G σp
 Рыночная модель di – доходность ценной бумаги i за данный период; d. I – доходность на рыночный индекс I за этот же период; αi. I – коэффициент смещения; βi. I – коэффициент наклона; εi. I – случайная погрешность. Предположив, что коэффициент наклона положителен, из уравнения можно заметить: чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги.
Рыночная модель di – доходность ценной бумаги i за данный период; d. I – доходность на рыночный индекс I за этот же период; αi. I – коэффициент смещения; βi. I – коэффициент наклона; εi. I – случайная погрешность. Предположив, что коэффициент наклона положителен, из уравнения можно заметить: чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги.
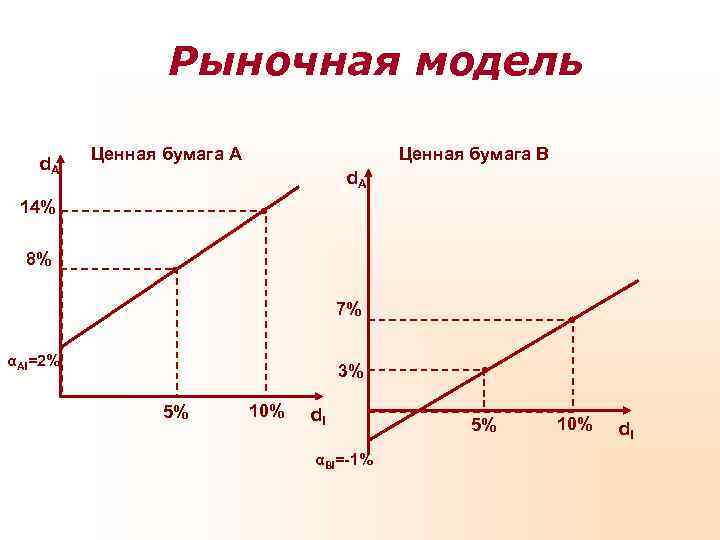
 Пример Рассмотрим акции А, для которых ai. I=2% и bi. I=1, 2. Это значит, что для акции А рыночная модель будет выглядеть: d. A=2%+1, 2 d. I+εAI Т. о. , если рыночный индекс имеет доходность 10%, то ожидаемая доходность ЦБ составляет 14% (2%+1, 2*10%). Если доходность рыночного индекса равняется -5%, то доходность ЦБ А ожидается равной -4% (2%+1, 2*(-5%)). Аналогично рассуждаем в отношении акций В, для которых αi. I = -1% и βi. I = 0, 8.
Пример Рассмотрим акции А, для которых ai. I=2% и bi. I=1, 2. Это значит, что для акции А рыночная модель будет выглядеть: d. A=2%+1, 2 d. I+εAI Т. о. , если рыночный индекс имеет доходность 10%, то ожидаемая доходность ЦБ составляет 14% (2%+1, 2*10%). Если доходность рыночного индекса равняется -5%, то доходность ЦБ А ожидается равной -4% (2%+1, 2*(-5%)). Аналогично рассуждаем в отношении акций В, для которых αi. I = -1% и βi. I = 0, 8.
 Рыночная модель Ценная бумага А Ценная бумага В d. А 14% 8% 7% αAI=2% 3% 5% 10% d. I αBI=-1%
Рыночная модель Ценная бумага А Ценная бумага В d. А 14% 8% 7% αAI=2% 3% 5% 10% d. I αBI=-1%
 Случайная погрешность (εAI) показывает, что рыночная модель не очень точно объясняет доходности ценных бумаг. Случайную погрешность можно рассматривать как случайную переменную, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, обозначенным σi. I.
Случайная погрешность (εAI) показывает, что рыночная модель не очень точно объясняет доходности ценных бумаг. Случайную погрешность можно рассматривать как случайную переменную, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, обозначенным σi. I.
 «Бета» -коэффициент Наклон в рыночной модели ценной бумаги измеряет чувствительность ее доходности к доходности на рыночный индекс. Коэффициент наклона рыночной модели часто называют «бета» -коэффициентом (beta) σi. I – ковариация между доходностью акции i и доходностью на рыночный индекс; σ2 i. I – дисперсия доходности на индекс; βi. I – коэффициент наклона.
«Бета» -коэффициент Наклон в рыночной модели ценной бумаги измеряет чувствительность ее доходности к доходности на рыночный индекс. Коэффициент наклона рыночной модели часто называют «бета» -коэффициентом (beta) σi. I – ковариация между доходностью акции i и доходностью на рыночный индекс; σ2 i. I – дисперсия доходности на индекс; βi. I – коэффициент наклона.
 «Бета» -коэффициент Акция, которая имеет доходность, являющуюся зеркальным отражением доходности на индекс, будет иметь «бета» -коэффициент, равный 1. (ему соответствует рыночная модель вида: di=d. I+ εi. I) То есть акции с «бета» -коэффициентом больше единицы (такие, как А) обладают большей изменчивостью, чем рыночный индекс, и носят название «агрессивные» акции. И наоборот, акции с «бета» -коэффициентом меньше единицы обладают меньшей изменчивостью, чем рыночный индекс, и называются «оборонительными» акциями.
«Бета» -коэффициент Акция, которая имеет доходность, являющуюся зеркальным отражением доходности на индекс, будет иметь «бета» -коэффициент, равный 1. (ему соответствует рыночная модель вида: di=d. I+ εi. I) То есть акции с «бета» -коэффициентом больше единицы (такие, как А) обладают большей изменчивостью, чем рыночный индекс, и носят название «агрессивные» акции. И наоборот, акции с «бета» -коэффициентом меньше единицы обладают меньшей изменчивостью, чем рыночный индекс, и называются «оборонительными» акциями.
 Диверсификация Исходя из рыночной модели, общий риск ценной бумаги, измеряемый ее дисперсией, состоит из двух частей: (1) рыночный (или систематический) риск; (2) собственный (или несистематический) риск σ2 i – дисперсия доходности на индекс; β 2 i. I σ2 i. I – рыночный риск ценной бумаги i; σ2 ε I - собственный риск ценной бумаги i.
Диверсификация Исходя из рыночной модели, общий риск ценной бумаги, измеряемый ее дисперсией, состоит из двух частей: (1) рыночный (или систематический) риск; (2) собственный (или несистематический) риск σ2 i – дисперсия доходности на индекс; β 2 i. I σ2 i. I – рыночный риск ценной бумаги i; σ2 ε I - собственный риск ценной бумаги i.
 Общий риск портфеля Если долю фондов инвестора, вложенную в ценную бумагу i данного портфеля р, обозначить через Xi, то доходность портфеля может быть вычислена по следующей формуле
Общий риск портфеля Если долю фондов инвестора, вложенную в ценную бумагу i данного портфеля р, обозначить через Xi, то доходность портфеля может быть вычислена по следующей формуле
 Общий риск портфеля, измеряемый дисперсией его доходности, выражается следующим образом Общий риск портфеля состоит из двух компонентов. Эти компоненты также носят название рыночного риска (β 2 p. I σ2 I) и собственного риска (σ2 εp).
Общий риск портфеля, измеряемый дисперсией его доходности, выражается следующим образом Общий риск портфеля состоит из двух компонентов. Эти компоненты также носят название рыночного риска (β 2 p. I σ2 I) и собственного риска (σ2 εp).
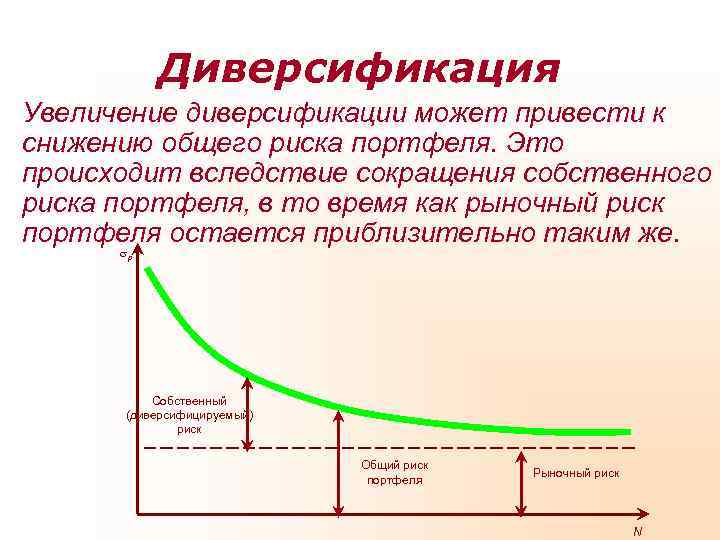
 Диверсификация Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же. p Собственный (диверсифицируемый) риск Общий риск Рыночный риск портфеля N
Диверсификация Увеличение диверсификации может привести к снижению общего риска портфеля. Это происходит вследствие сокращения собственного риска портфеля, в то время как рыночный риск портфеля остается приблизительно таким же. p Собственный (диверсифицируемый) риск Общий риск Рыночный риск портфеля N
 Рыночный риск портфеля Диверсификация приводит к усреднению рыночного риска Этот вывод имеет важное значение, так как в случае плохого или хорошего экономического прогноза большинство ценных бумаг упадут или соответственно возрастут в цене. Несмотря на уровень диверсификации портфеля, всегда можно ожидать, что такие рыночные явления будут влиять на доходность портфеля.
Рыночный риск портфеля Диверсификация приводит к усреднению рыночного риска Этот вывод имеет важное значение, так как в случае плохого или хорошего экономического прогноза большинство ценных бумаг упадут или соответственно возрастут в цене. Несмотря на уровень диверсификации портфеля, всегда можно ожидать, что такие рыночные явления будут влиять на доходность портфеля.
 Собственный риск портфеля Диверсификация существенно уменьшает собственный риск. Портфель, состоящий из 30 или более случайно выбранных ценных бумаг, будет иметь относительно низкую величину собственного риска. Это означает, что общий риск будет ненамного больше величины имеющегося рыночного риска.
Собственный риск портфеля Диверсификация существенно уменьшает собственный риск. Портфель, состоящий из 30 или более случайно выбранных ценных бумаг, будет иметь относительно низкую величину собственного риска. Это означает, что общий риск будет ненамного больше величины имеющегося рыночного риска.
 Тема 5. Безрисковое предоставление и получение займов
Тема 5. Безрисковое предоставление и получение займов
 Содержание темы 5. 1. Безрисковый актив 5. 2. Безрисковое кредитование и безрисковое заимствование 5. 3. Заимствование и инвестирование в рискованные ценные бумаги 5. 4. Заимствование и инвестирование в рискованный портфель. Влияние безрискового заимствования и кредитования на выбор портфеля
Содержание темы 5. 1. Безрисковый актив 5. 2. Безрисковое кредитование и безрисковое заимствование 5. 3. Заимствование и инвестирование в рискованные ценные бумаги 5. 4. Заимствование и инвестирование в рискованный портфель. Влияние безрискового заимствования и кредитования на выбор портфеля
 Безрисковое предоставление и получение займов Подход Марковица к инвестициям обобщается: 1. Инвестору разрешается инвестировать не только в рискованные, но и в безрисковые активы. (Имеется N активов, доступных для инвестиций, включая (N-1) рискованный актив и один безрисковый). 2. Инвестору разрешается одалживать деньги при обязательных выплатах по определенной процентной ставке по взятым займам. Рассматривается эффект от добавления безрискового актива к набору рискованных активов.
Безрисковое предоставление и получение займов Подход Марковица к инвестициям обобщается: 1. Инвестору разрешается инвестировать не только в рискованные, но и в безрисковые активы. (Имеется N активов, доступных для инвестиций, включая (N-1) рискованный актив и один безрисковый). 2. Инвестору разрешается одалживать деньги при обязательных выплатах по определенной процентной ставке по взятым займам. Рассматривается эффект от добавления безрискового актива к набору рискованных активов.
 Безрисковый актив Если инвестор покупает безрисковый актив в начале инвестиционного периода, то он точно знает, какова будет его стоимость в конце периода. Поскольку неопределенность конечной стоимости безрискового актива отсутствует, то, по определению, стандартное отклонение для безрискового актива равно нулю. Поскольку все корпоративные ЦБ имеют некоторую вероятность неуплаты, то безрисковый актив не может быть выпущен корпорацией => безрисковым активом может быть лишь ценная бумага, выпущенная правительством.
Безрисковый актив Если инвестор покупает безрисковый актив в начале инвестиционного периода, то он точно знает, какова будет его стоимость в конце периода. Поскольку неопределенность конечной стоимости безрискового актива отсутствует, то, по определению, стандартное отклонение для безрискового актива равно нулю. Поскольку все корпоративные ЦБ имеют некоторую вероятность неуплаты, то безрисковый актив не может быть выпущен корпорацией => безрисковым активом может быть лишь ценная бумага, выпущенная правительством.
 ЦБ, выпущенные правительством ЦБ со сроком погашения большим, чем период владения (Процентная ставка может меняться непредвиденным образом в течение периода владения). ЦБ со сроком погашения меньшим, чем период владения (Не известна процентная ставка, по которой могут быть реинвестированы доходы на остаток периода владения). ЦБ со сроком погашения, совпадающим с периодом владения.
ЦБ, выпущенные правительством ЦБ со сроком погашения большим, чем период владения (Процентная ставка может меняться непредвиденным образом в течение периода владения). ЦБ со сроком погашения меньшим, чем период владения (Не известна процентная ставка, по которой могут быть реинвестированы доходы на остаток периода владения). ЦБ со сроком погашения, совпадающим с периодом владения.
 Безрисковое кредитование Инвестирование в безрисковый актив часто называют безрисковым кредитованием
Безрисковое кредитование Инвестирование в безрисковый актив часто называют безрисковым кредитованием
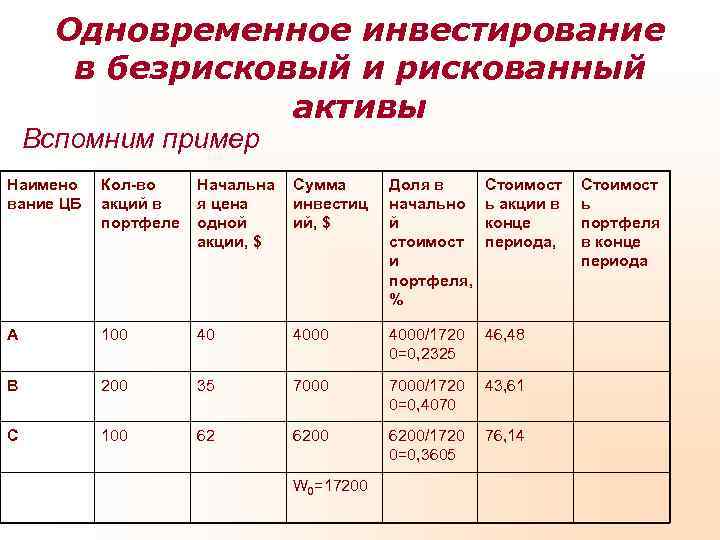
 Одновременное инвестирование в безрисковый и рискованный активы Вспомним пример Наимено Кол-во Начальна Сумма Доля в Стоимост вание ЦБ акций в я цена инвестиц начально ь акции в ь портфеле одной ий, $ й конце портфеля акции, $ стоимост периода, в конце и периода портфеля, % А 100 4000/1720 46, 48 0=0, 2325 В 200 35 7000/1720 43, 61 0=0, 4070 С 100 6200/1720 76, 14 0=0, 3605 W 0=17200
Одновременное инвестирование в безрисковый и рискованный активы Вспомним пример Наимено Кол-во Начальна Сумма Доля в Стоимост вание ЦБ акций в я цена инвестиц начально ь акции в ь портфеле одной ий, $ й конце портфеля акции, $ стоимост периода, в конце и периода портфеля, % А 100 4000/1720 46, 48 0=0, 2325 В 200 35 7000/1720 43, 61 0=0, 4070 С 100 6200/1720 76, 14 0=0, 3605 W 0=17200
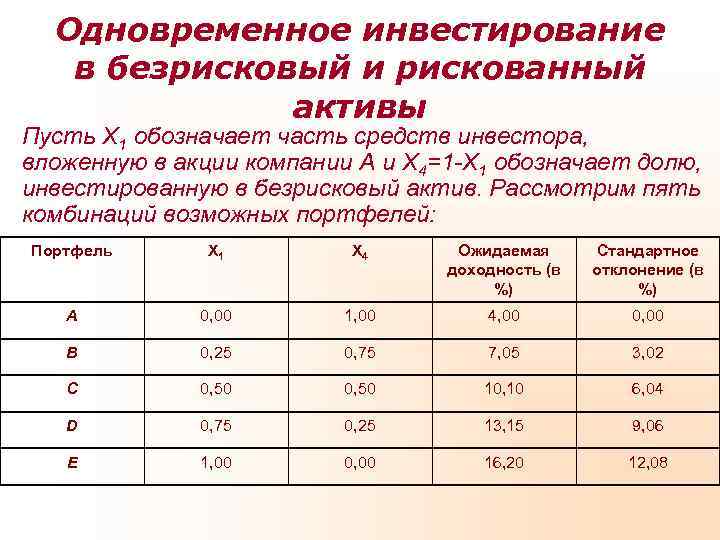
 Одновременное инвестирование в безрисковый и рискованный активы Пусть Х 1 обозначает часть средств инвестора, вложенную в акции компании А и Х 4=1 -Х 1 обозначает долю, инвестированную в безрисковый актив. Рассмотрим пять комбинаций возможных портфелей: Портфель Х 1 Х 4 Ожидаемая Стандартное доходность (в отклонение (в %) A 0, 00 1, 00 4, 00 0, 00 B 0, 25 0, 75 7, 05 3, 02 C 0, 50 10, 10 6, 04 D 0, 75 0, 25 13, 15 9, 06 E 1, 00 0, 00 16, 20 12, 08
Одновременное инвестирование в безрисковый и рискованный активы Пусть Х 1 обозначает часть средств инвестора, вложенную в акции компании А и Х 4=1 -Х 1 обозначает долю, инвестированную в безрисковый актив. Рассмотрим пять комбинаций возможных портфелей: Портфель Х 1 Х 4 Ожидаемая Стандартное доходность (в отклонение (в %) A 0, 00 1, 00 4, 00 0, 00 B 0, 25 0, 75 7, 05 3, 02 C 0, 50 10, 10 6, 04 D 0, 75 0, 25 13, 15 9, 06 E 1, 00 0, 00 16, 20 12, 08
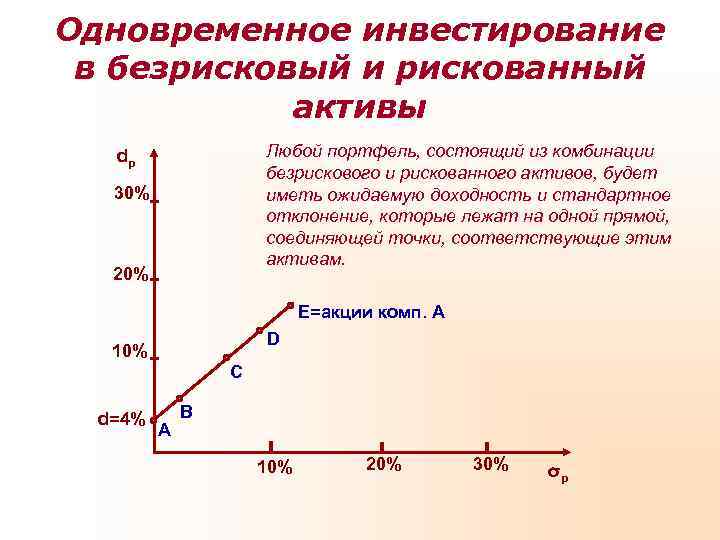
 Одновременное инвестирование в безрисковый и рискованный активы dp Любой портфель, состоящий из комбинации безрискового и рискованного активов, будет 30% иметь ожидаемую доходность и стандартное отклонение, которые лежат на одной прямой, соединяющей точки, соответствующие этим активам. 20% E=акции комп. A D 10% C d=4% B A 10% 20% 30% σp
Одновременное инвестирование в безрисковый и рискованный активы dp Любой портфель, состоящий из комбинации безрискового и рискованного активов, будет 30% иметь ожидаемую доходность и стандартное отклонение, которые лежат на одной прямой, соединяющей точки, соответствующие этим активам. 20% E=акции комп. A D 10% C d=4% B A 10% 20% 30% σp
 Одновременное инвестирование в безрисковый актив и рискованный портфель Рассмотрим, что происходит, когда портфель, состоящий из более чем одной ЦБ, объединяется с безрисковым активом. Пример: Рассмотрим портфель РАС, состоящий из акций компаний А и В в долях 0, 8 и 0, 2 соответственно.
Одновременное инвестирование в безрисковый актив и рискованный портфель Рассмотрим, что происходит, когда портфель, состоящий из более чем одной ЦБ, объединяется с безрисковым активом. Пример: Рассмотрим портфель РАС, состоящий из акций компаний А и В в долях 0, 8 и 0, 2 соответственно.
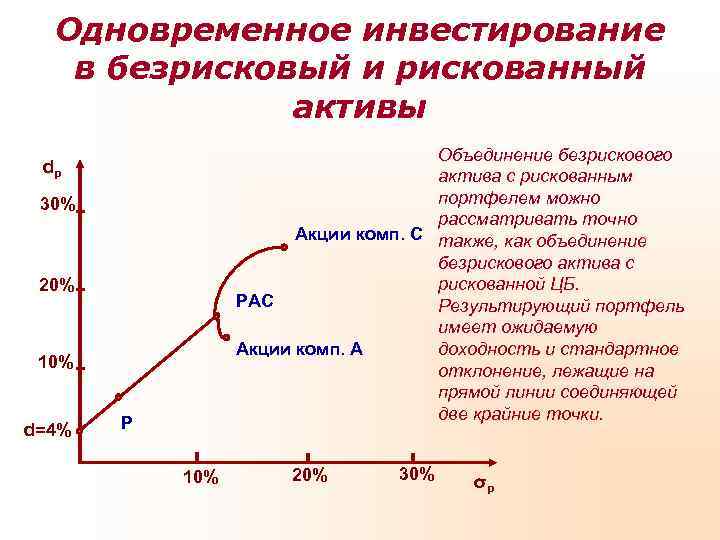
 Одновременное инвестирование в безрисковый и рискованный активы Объединение безрискового dp актива с рискованным 30% портфелем можно рассматривать точно Акции комп. С также, как объединение безрискового актива с 20% рискованной ЦБ. РАС Результирующий портфель имеет ожидаемую Акции комп. А доходность и стандартное 10% отклонение, лежащие на прямой линии соединяющей две крайние точки. d=4% Р 10% 20% 30% σp
Одновременное инвестирование в безрисковый и рискованный активы Объединение безрискового dp актива с рискованным 30% портфелем можно рассматривать точно Акции комп. С также, как объединение безрискового актива с 20% рискованной ЦБ. РАС Результирующий портфель имеет ожидаемую Акции комп. А доходность и стандартное 10% отклонение, лежащие на прямой линии соединяющей две крайние точки. d=4% Р 10% 20% 30% σp
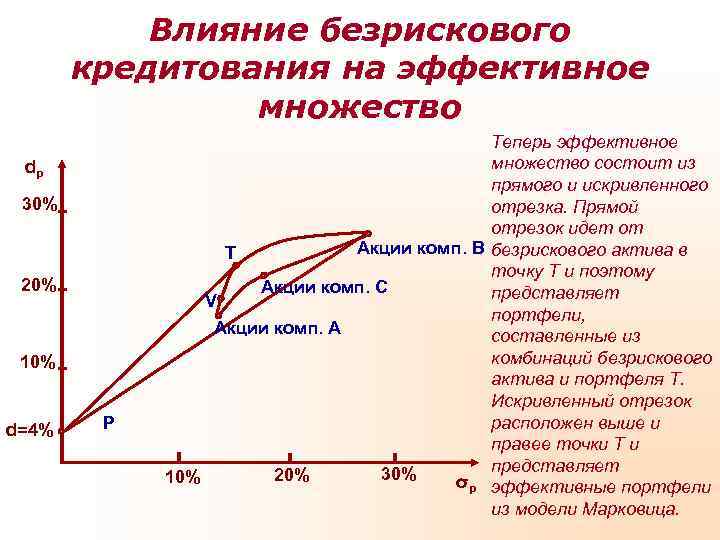
 Влияние безрискового кредитования на эффективное множество Теперь эффективное dp множество состоит из прямого и искривленного 30% отрезка. Прямой отрезок идет от Т Акции комп. В безрискового актива в точку Т и поэтому 20% Акции комп. С представляет V портфели, Акции комп. А составленные из 10% комбинаций безрискового актива и портфеля Т. Искривленный отрезок d=4% Р расположен выше и правее точки Т и 20% 30% представляет 10% σp эффективные портфели из модели Марковица.
Влияние безрискового кредитования на эффективное множество Теперь эффективное dp множество состоит из прямого и искривленного 30% отрезка. Прямой отрезок идет от Т Акции комп. В безрискового актива в точку Т и поэтому 20% Акции комп. С представляет V портфели, Акции комп. А составленные из 10% комбинаций безрискового актива и портфеля Т. Искривленный отрезок d=4% Р расположен выше и правее точки Т и 20% 30% представляет 10% σp эффективные портфели из модели Марковица.
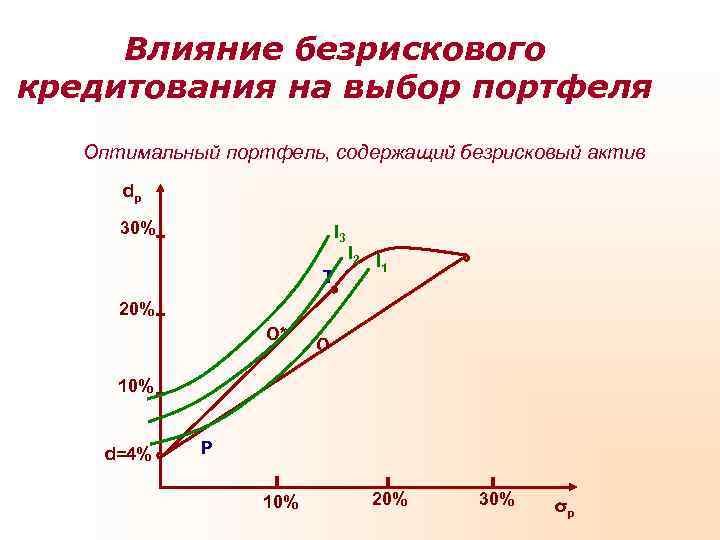
 Влияние безрискового кредитования на выбор портфеля Оптимальный портфель, содержащий безрисковый актив dp 30% I 3 I 2 I 1 Т 20% O* O 10% d=4% Р 10% 20% 30% σp
Влияние безрискового кредитования на выбор портфеля Оптимальный портфель, содержащий безрисковый актив dp 30% I 3 I 2 I 1 Т 20% O* O 10% d=4% Р 10% 20% 30% σp
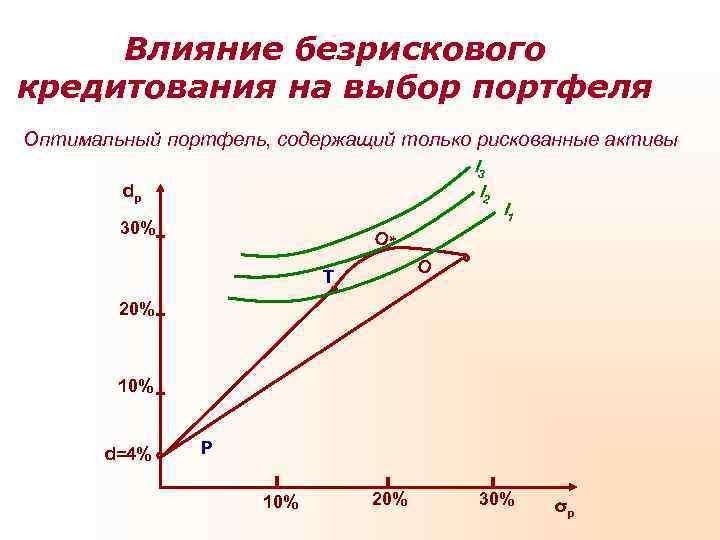
 Влияние безрискового кредитования на выбор портфеля Оптимальный портфель, содержащий только рискованные активы I 3 dp I 2 I 1 30% O* O Т 20% 10% d=4% Р 10% 20% 30% σp
Влияние безрискового кредитования на выбор портфеля Оптимальный портфель, содержащий только рискованные активы I 3 dp I 2 I 1 30% O* O Т 20% 10% d=4% Р 10% 20% 30% σp
 Безрисковое заимствование Если процентная ставка известна и неопределенность с выплатой займа отсутствует, то это часто называется безрисковым заимствованием Предполагается, что процентная ставка по займу равна ставке, которая может быть заработана инвестированием в безрисковые активы.
Безрисковое заимствование Если процентная ставка известна и неопределенность с выплатой займа отсутствует, то это часто называется безрисковым заимствованием Предполагается, что процентная ставка по займу равна ставке, которая может быть заработана инвестированием в безрисковые активы.
 Заимствование и инвестирование в рискованные ценные бумаги Для оценки влияния безрисковых займов на эффективное множество обобщим предыдущий пример. Рассмотрим портфели F, H, G и I, соответствующие инвестициям как собственных средств инвестора, так и полученных взаймы, в акции компании А.
Заимствование и инвестирование в рискованные ценные бумаги Для оценки влияния безрисковых займов на эффективное множество обобщим предыдущий пример. Рассмотрим портфели F, H, G и I, соответствующие инвестициям как собственных средств инвестора, так и полученных взаймы, в акции компании А.
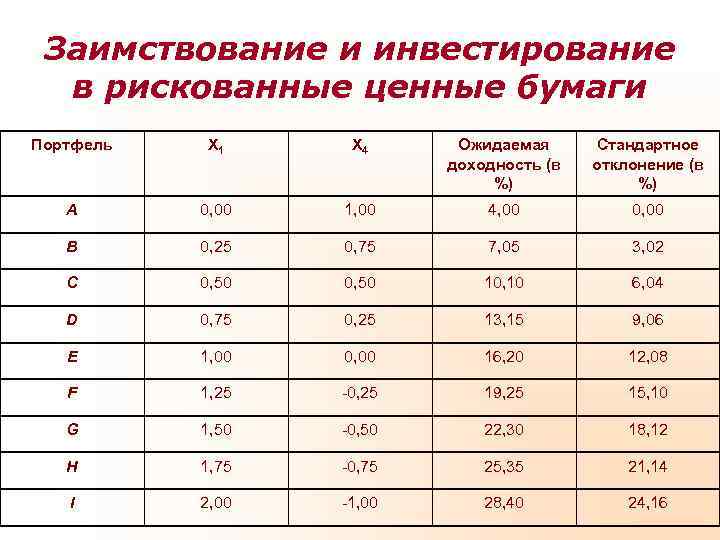
 Заимствование и инвестирование в рискованные ценные бумаги Портфель Х 1 Х 4 Ожидаемая Стандартное доходность (в отклонение (в %) A 0, 00 1, 00 4, 00 0, 00 B 0, 25 0, 75 7, 05 3, 02 C 0, 50 10, 10 6, 04 D 0, 75 0, 25 13, 15 9, 06 E 1, 00 0, 00 16, 20 12, 08 F 1, 25 -0, 25 19, 25 15, 10 G 1, 50 -0, 50 22, 30 18, 12 H 1, 75 -0, 75 25, 35 21, 14 I 2, 00 -1, 00 28, 40 24, 16
Заимствование и инвестирование в рискованные ценные бумаги Портфель Х 1 Х 4 Ожидаемая Стандартное доходность (в отклонение (в %) A 0, 00 1, 00 4, 00 0, 00 B 0, 25 0, 75 7, 05 3, 02 C 0, 50 10, 10 6, 04 D 0, 75 0, 25 13, 15 9, 06 E 1, 00 0, 00 16, 20 12, 08 F 1, 25 -0, 25 19, 25 15, 10 G 1, 50 -0, 50 22, 30 18, 12 H 1, 75 -0, 75 25, 35 21, 14 I 2, 00 -1, 00 28, 40 24, 16
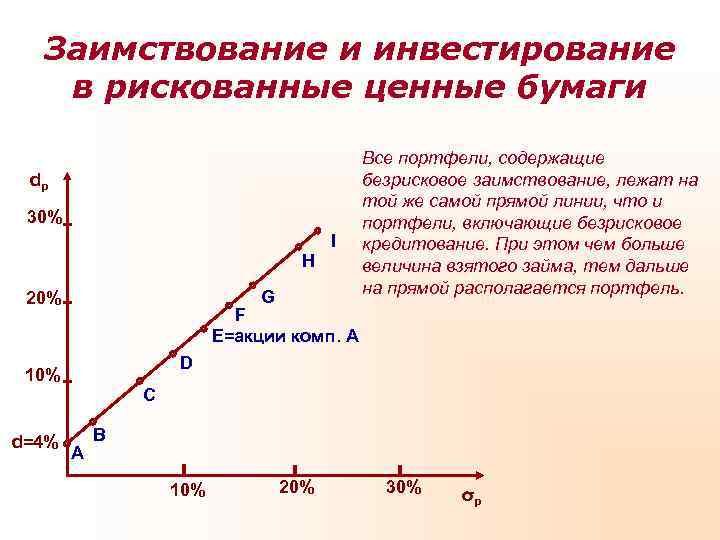
 Заимствование и инвестирование в рискованные ценные бумаги Все портфели, содержащие dp безрисковое заимствование, лежат на той же самой прямой линии, что и 30% портфели, включающие безрисковое I кредитование. При этом чем больше H величина взятого займа, тем дальше на прямой располагается портфель. 20% G F E=акции комп. A D 10% C d=4% B A 10% 20% 30% σp
Заимствование и инвестирование в рискованные ценные бумаги Все портфели, содержащие dp безрисковое заимствование, лежат на той же самой прямой линии, что и 30% портфели, включающие безрисковое I кредитование. При этом чем больше H величина взятого займа, тем дальше на прямой располагается портфель. 20% G F E=акции комп. A D 10% C d=4% B A 10% 20% 30% σp
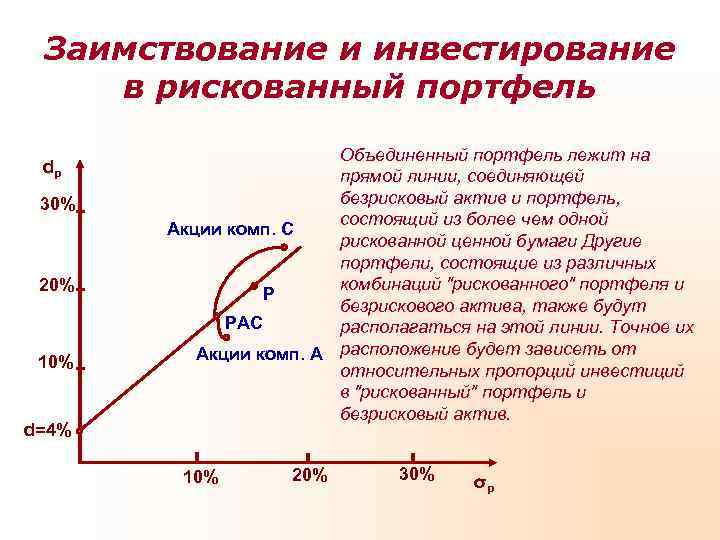
 Заимствование и инвестирование в рискованный портфель Объединенный портфель лежит на dp прямой линии, соединяющей 30% безрисковый актив и портфель, состоящий из более чем одной Акции комп. С рискованной ценной бумаги Другие портфели, состоящие из различных 20% комбинаций "рискованного" портфеля и Р безрискового актива, также будут РАС располагаться на этой линии. Точное их 10% Акции комп. А расположение будет зависеть от относительных пропорций инвестиций в "рискованный" портфель и безрисковый актив. d=4% 10% 20% 30% σp
Заимствование и инвестирование в рискованный портфель Объединенный портфель лежит на dp прямой линии, соединяющей 30% безрисковый актив и портфель, состоящий из более чем одной Акции комп. С рискованной ценной бумаги Другие портфели, состоящие из различных 20% комбинаций "рискованного" портфеля и Р безрискового актива, также будут РАС располагаться на этой линии. Точное их 10% Акции комп. А расположение будет зависеть от относительных пропорций инвестиций в "рискованный" портфель и безрисковый актив. d=4% 10% 20% 30% σp
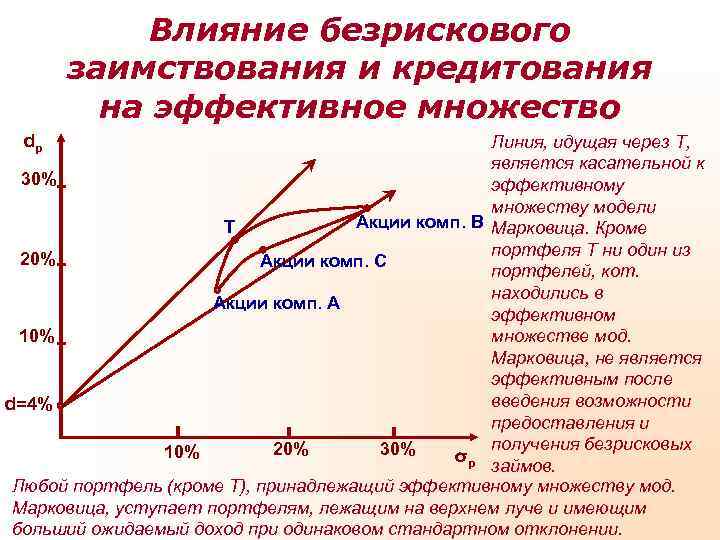
 Влияние безрискового заимствования и кредитования на эффективное множество dp Линия, идущая через Т, является касательной к 30% эффективному множеству модели Т Акции комп. В Марковица. Кроме портфеля Т ни один из 20% Акции комп. С портфелей, кот. находились в Акции комп. А эффективном 10% множестве мод. Марковица, не является эффективным после d=4% введения возможности предоставления и 10% 20% 30% получения безрисковых σp займов. Любой портфель (кроме Т), принадлежащий эффективному множеству мод. Марковица, уступает портфелям, лежащим на верхнем луче и имеющим больший ожидаемый доход при одинаковом стандартном отклонении.
Влияние безрискового заимствования и кредитования на эффективное множество dp Линия, идущая через Т, является касательной к 30% эффективному множеству модели Т Акции комп. В Марковица. Кроме портфеля Т ни один из 20% Акции комп. С портфелей, кот. находились в Акции комп. А эффективном 10% множестве мод. Марковица, не является эффективным после d=4% введения возможности предоставления и 10% 20% 30% получения безрисковых σp займов. Любой портфель (кроме Т), принадлежащий эффективному множеству мод. Марковица, уступает портфелям, лежащим на верхнем луче и имеющим больший ожидаемый доход при одинаковом стандартном отклонении.
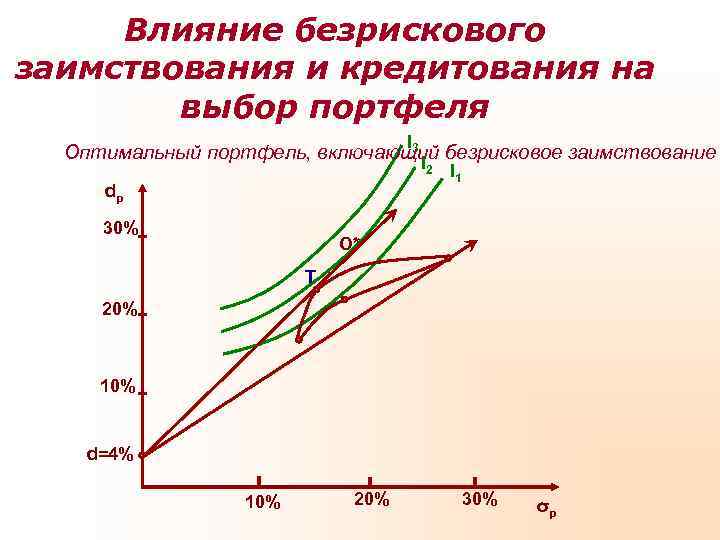
 Влияние безрискового заимствования и кредитования на выбор портфеля I Оптимальный портфель, включающий безрисковое заимствование 3 I 2 I 1 dp 30% O* Т 20% 10% d=4% 10% 20% 30% σp
Влияние безрискового заимствования и кредитования на выбор портфеля I Оптимальный портфель, включающий безрисковое заимствование 3 I 2 I 1 dp 30% O* Т 20% 10% d=4% 10% 20% 30% σp
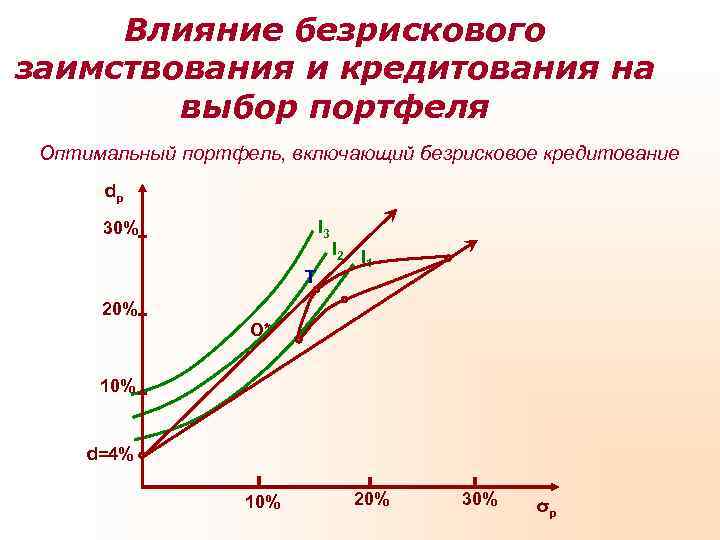
 Влияние безрискового заимствования и кредитования на выбор портфеля Оптимальный портфель, включающий безрисковое кредитование dp 30% I 3 I 2 I 1 Т 20% O* 10% d=4% 10% 20% 30% σp
Влияние безрискового заимствования и кредитования на выбор портфеля Оптимальный портфель, включающий безрисковое кредитование dp 30% I 3 I 2 I 1 Т 20% O* 10% d=4% 10% 20% 30% σp

