IFT-17584 Semaine 04 Programmation système Pierre Marchand 2002

IFT-17584 Semaine 04 Programmation système @Pierre Marchand, 2002 59

Plan de la rencontre • • Retour sur la semaine précédente Comparaison Branchements Structure de contrôle Chaînes de caractères et tableaux Instructions logiques Instructions arithmétiques @Pierre Marchand, 2002 60

La semaine précédente • Les modes d’adressages • La gestion de la piles • Le passage des arguments @Pierre Marchand, 2002 61

Comparaison Lors d'une comparaison, par exemple cmp a, b, le processeur effectue la soustraction a – b et positionne les indicateurs selon le résultat de l'opération. Les indicateurs qui nous intéressent ici sont : § ZF = zero flag = 1 si le résultat est nul, sinon ZF = 0, § CF = carry flag = 1 si une retenue est générée, sinon CF = 0, § SF = sign flag = 1 si le résultat est négatif, sinon SF = 0, § OF = overflow flag = 1 s'il y a débordement de capacité, sinon OF = 0 On rappelle qu’un débordement de capacité a lieu si, lors d’une opération sur des opérandes de même signe, le résultat est de signe différent. @Pierre Marchand, 2002 62

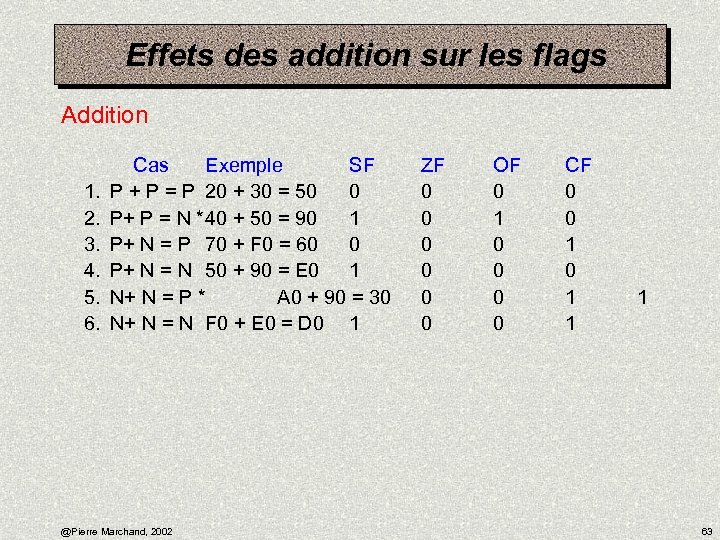Effets des addition sur les flags Addition 1. 2. 3. 4. 5. 6. Cas Exemple SF P + P = P 20 + 30 = 50 0 P+ P = N *40 + 50 = 90 1 P+ N = P 70 + F 0 = 60 0 P+ N = N 50 + 90 = E 0 1 N+ N = P * A 0 + 90 = 30 N+ N = N F 0 + E 0 = D 0 1 @Pierre Marchand, 2002 ZF 0 0 0 OF 0 1 0 0 CF 0 0 1 1 1 63

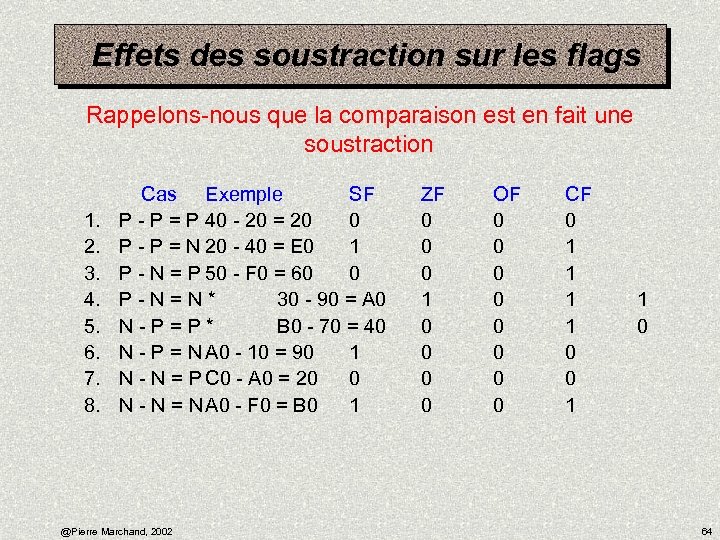Effets des soustraction sur les flags Rappelons-nous que la comparaison est en fait une soustraction 1. 2. 3. 4. 5. 6. 7. 8. Cas Exemple SF P - P = P 40 - 20 = 20 0 P - P = N 20 - 40 = E 0 1 P - N = P 50 - F 0 = 60 0 P - N = N * 30 - 90 = A 0 N - P = P * B 0 - 70 = 40 N - P = N A 0 - 10 = 90 1 N - N = P C 0 - A 0 = 20 0 N - N = N A 0 - F 0 = B 0 1 @Pierre Marchand, 2002 ZF 0 0 0 1 0 0 OF 0 0 0 0 CF 0 1 1 0 64

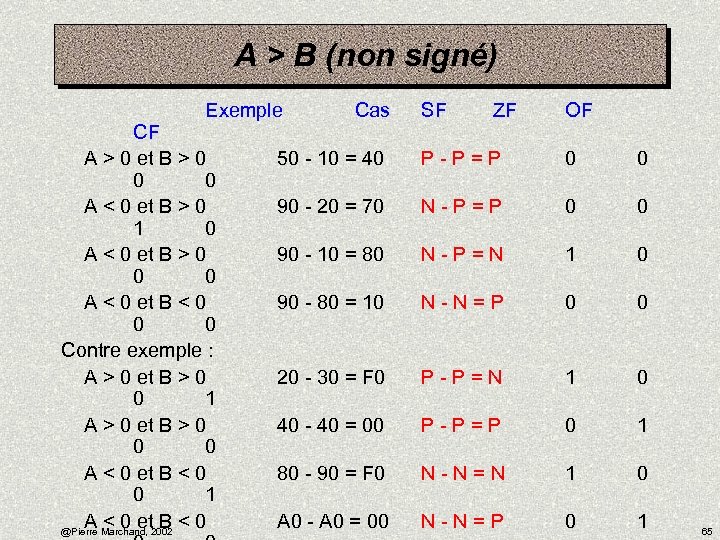A > B (non signé) Exemple Cas CF A > 0 et B > 0 50 - 10 = 40 0 0 A < 0 et B > 0 90 - 20 = 70 1 0 A < 0 et B > 0 90 - 10 = 80 0 0 A < 0 et B < 0 90 - 80 = 10 0 0 Contre exemple : A > 0 et B > 0 20 - 30 = F 0 0 1 A > 0 et B > 0 40 - 40 = 00 0 0 A < 0 et B < 0 80 - 90 = F 0 0 1 A < 0 et B < 0 A 0 - A 0 = 00 @Pierre Marchand, 2002 SF ZF OF P - P = P 0 0 N - P = N 1 0 N - N = P 0 0 P - P = N 1 0 P - P = P 0 1 N - N = N 1 0 N - N = P 0 1 65

comparaisons non signés On peut dériver de la sorte les conditions suivantes pour des quantités non signées: § a (above) ZF = 0 et CF = 0 > § ae (above or equal)CF = 0 >= § b (below) CF = 1 < § be (below or equal) CF = 1 ou ZF = 1 <= @Pierre Marchand, 2002 66

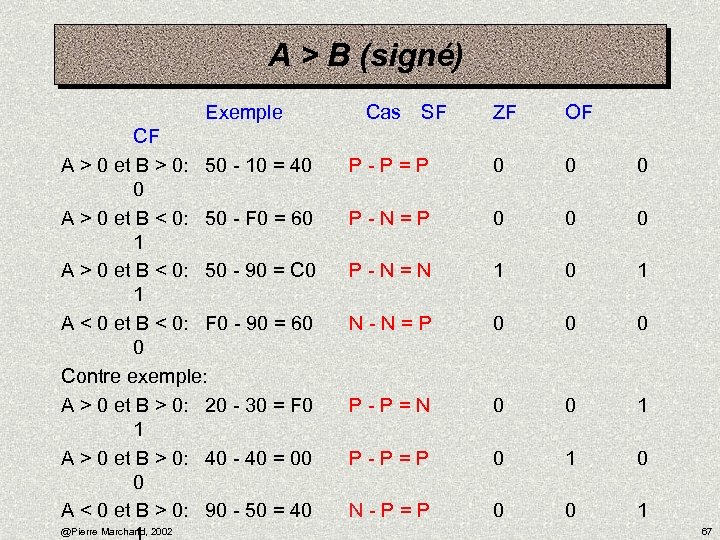A > B (signé) Exemple CF A > 0 et B > 0: 50 - 10 = 40 0 A > 0 et B < 0: 50 - F 0 = 60 1 A > 0 et B < 0: 50 - 90 = C 0 1 A < 0 et B < 0: F 0 - 90 = 60 0 Contre exemple: A > 0 et B > 0: 20 - 30 = F 0 1 A > 0 et B > 0: 40 - 40 = 00 0 A < 0 et B > 0: 90 - 50 = 40 @Pierre Marchand, 2002 Cas SF ZF OF P - P = P 0 0 0 P - N = N 1 0 1 N - N = P 0 0 0 P - P = N 0 0 1 P - P = P 0 1 0 N - P = P 0 0 1 67

Comparaisons signés On peut de la même façon dériver les conditions suivantes pour les quantités signées : § g (greater) ZF = 0 et SF = OF § ge (greater or equal) SF = OF § l (less) SF OF § le (less or equal) ZF = 1 ou SF OF @Pierre Marchand, 2002 68

Branchements inconditionnels call jmp jump ret, retn, retf, iret @Pierre Marchand, 2002 return (near, far), interrupt return 69

Branchements conditionnels simple je jne jz jnz jump if equal: jump if not equal: jump if zero: jump if not zero: @Pierre Marchand, 2002 ZF = 1 ZF = 0 70

Branchements conditionnels non signés ja jna jae jnae jb jnb jbe jnbe jump above (x > y non-signé ) CF = 0 & ZF = 0 jump not above = jbe jump above or equal CF = 0 jump not above or equal = jb jump below (x < y non-signé) CF = 1 jump not below = jae jump below or equal CF = 1 | ZF = 1 jump not below or equal = ja @Pierre Marchand, 2002 71

Branchements conditionnels pures Sur les indicateurs eux mêmes jc jnc jo jno jp jnp jpo js jns jump if carry: CF = 1 jump if not carry: CF = 0 jump if overflow: OF = 1 jump if not overflow: OF = 0 jump if parity: PF = 1 jump if not parity: PF = 0 jump if parity odd: PF = 0 jump if sign: SF = 1 (negative) jump if no sign: SF = 0 @Pierre Marchand, 2002 72

Branchements conditionnels signés jg jng jge jnge jl jnl jle jnle jump greater (x > y signé) SF = OF & ZF = 0 jump not greater SF != OF & ZF = 1 jump greater or equal SF = OF jump not greater or equal = jl jump less (x < y signé) SF != OF jump not less = jge jump less or equal SF != OF jump not less or equal = jg @Pierre Marchand, 2002 73

Branchements sur compteur jcxz jump if cx = 0 jecxz jump if ecx = 0 @Pierre Marchand, 2002 74

Variables signés ou non signés Il faut bien prendre garde d'utiliser le bon branchement selon le type de données considéré. En C, les variables sont signées par défaut. Pour avoir des variables non signées, on utilise la déclaration unsigned. Exemples : unsigned char x; unsigned short y; unsigned long z; 0 ≤ x ≤ 255 0 ≤ y ≤ 65535 0 ≤ z ≤ 4294967295 char x; short y; long z; -128 ≤ x ≤ 127 -32768 ≤ y ≤ 32767 -2147483648 ≤ z ≤ 2147483647 @Pierre Marchand, 2002 75

Structure de contrôle • • • if simple if complexe while for switch @Pierre Marchand, 2002 76

if simple if ( a > b ) { … } else: endif: jng … … jmp … … … cmp else a, b endif Démontré dans l’exemple 01 disponible sur le site @Pierre Marchand, 2002 77

if complexe if ( ( a > b ) && ( c <= d ) ) { if: cmp a, b … jng endif … cmp c, d } jnle endif … … endif: Démontré dans l’exemple 01 @Pierre Marchand, 2002 78

while ( a > b ) { while: cmp … jng … … } … jmp endwhile: a, b endwhile … Démontré dans l’exemple 01 @Pierre Marchand, 2002 79

for ( i = 1; i < 10; i ++ ) { for: mov i, 1 … jmp test … next: … … … } inc i test: cmp i, 10 jl next endfor: … Démontré dans l’exemple 01 @Pierre Marchand, 2002 80

Instructions de boucle LOOP/LOOPW/LOOPD Loop Boucle vers une étiquette. Décrémente ecx en mode 32 bits ou cx en mode 16 bits (sans affecter aucun indicateur). Si (e)cx est 0 après avoir été décrémenté, l’exécution continue à l’instruction suivante. On peut forcer un comptage sur cx avec loopw et sur ecx avec loopd. L’étiquette doit être à moins de -128 à + 127 octets de l’instruction loop. oszapc = oszapc loop étiquette 8 Démontré dans l’exemple 01 @Pierre Marchand, 2002 81

Instructions de boucle avec condition LOOPcc/LOOPcc. W/LOOPcc. D Loop Conditionally Boucle vers une étiquette tant que la condition est remplie et que (e)cx n’est pas 0. Décrémente ecx en mode 32 bits ou cx en mode 16 bits (sans affecter aucun indicateur). Si (e)cx est 0 après avoir été décrémenté, l’exécution continue à l’instruction suivante. On peut forcer un comptage sur cx avec loopw et sur ecx avec loopd. L’étiquette doit être à moins de -128 à + 127 octets de l’instruction loop. oszapc = oszapc loope étiquette 8 loopz(w) étiquette 8 loopne(d) étiquette 8 Démontré dans l’exemple 01 @Pierre Marchand, 2002 82

Remplacement des instructions de boucle On peut remplacer avantageusement loop par les instructions qu’elle remplace : dec ecx ; ou dec cx 0. 5 jnz boucle ~0. 5 Idem pour loopcc : ; pour simuler loopz … ; comparaison ou test jnz fin. Boucle dec ecx jnz boucle fin. Boucle : Dans ce dernier cas il y a une petite différence. Si on sort de la boucle parce que ecx est 0, alors ZF = 1, tandis qu’avec loopcc ZF=1 seulement si la condition testée est 0. Il faut donc modifier légèrement le code subséquent. @Pierre Marchand, 2002 83

Chaînes de caractères Types de chaînes Chaîne C Toto ‘T’, ‘o’, ‘t’, ‘o’, Chaîne Pascal Toto 4, ‘T’, ‘o’, ‘t’, ‘o’ @Pierre Marchand, 2002 84

Chaînes et tableaux Intel appelle également « chaîne » des tableaux de short, de long et autres. Un tableau est défini comme suit en C : short Tableau[n]; // Tableau de n short non initialisés short Tableau[ ] = { 0, 2, -3, 4, 20 }; // Tableau de 5 shorts Pour accéder à un élément d’un tableau, il y a deux façons : x = Tableau[i]; ou, si short * p = Tableau; alors x = *(p + 2 * i); // * 2 parce que short = 2 octets @Pierre Marchand, 2002 85

Adressage des chaînes et tableaux Pour accéder à un tableau en assembleur, on fait lea esi, Tableau ; ou mov esi, offset Tableau Ensuite, on utilise l’adressage indexé : mov ebx, i mov ax, [esi+ebx*2] mov x, ax @Pierre Marchand, 2002 86

Comparaison des chaînes et tableaux CMPSB CMPSW CMPSD Compare String Byte Compare String Word Compare String Double. Word Compare l’octet, le mot ou le double mot pointé par esi avec l’octet, le mot ou le double mot pointé par edi. Les pointeurs esi et edi sont avancés automatiquement de 1, 2, ou 4 selon qu’il s’agit d’un octet, d’un mot ou d’un double mot. Si l’indicateur de direction DF est 0, esi et edi sont incrémentés. S’il est 1, esi et edi sont décrémentés. @Pierre Marchand, 2002 87

Répétition des instruction de chaîne Cette instruction est souvent précédée de l’instruction REP ou REPcc. REPNE (ou REPNZ) est utilisé pour trouver la première correspondance entre deux chaînes. REPE est utilisé pour trouver la première différence entre deux chaînes. Avant la comparaison, ecx doit contenir le nombre maximum d’éléments à comparer. oszapc = cmps byte ptr [esi] cmpsb repne cmpsw Attention, le résultat est l’inverse de cmp fait dest - source cmps fait source - dest @Pierre Marchand, 2002 88

Instructions rep REP Repeat String Répète une instruction de chaîne le nombre de fois indiqué dans ecx. oszapc = oszapc rep répéter tant que ecx ≠ 0 repe, repz répéter tant que source = destination et ecx ≠ 0 repne, repnz répéter tant que source ≠ destination et ecx ≠ 0 @Pierre Marchand, 2002 89

Autres instructions de chaînes SCAS/SCASB/SCASW/SCASD Scan String Flags Dans le cas de SCAS, un opérande doit être fourni pour indiquer la taille des éléments à traiter. À la fin de l’instruction, edi pointe vers l’élément suivant. Si ecx = 0, edi pointe vers l’élément qui suit la dernière comparaison. L’indicateur ZF est affecté selon le résultat de la dernière comparaison et non selon la valeur de ecx. oszapc = ± ± ± scas word ptr [edi| 4 repne scasb 4 repe scasw 4 @Pierre Marchand, 2002 90

Charger une chaîne ou un tableaux LODS/LODSB/LODSW/LODSD Load Acc. from String Charge l’accumulateur avec un élément d’une chaîne en mémoire. esi doit pointer vers l’élément source, même si un opérande est fourni. Pour chaque élément chargé, esi est ajusté selon la taille de l’opérande et l’indicateur de direction DF. esi est incrémenté si DF = 0 et décrémenté si DF = 1. oszapc = oszapc lods word ptr [esi] lodsb lodsw lodsd Cette instruction ne peut pas être utilisée avec rep. @Pierre Marchand, 2002 91

Écrire une chaînes en mémoire STOS/STOSB/STOSW/STOSD Store String Data Copie la valeur de AL, AX ou EAX dans un emplacement mémoire dont l'adresse est contenue dans EDI (ES: DI). Ensuite, EDI est ajusté selon la taille de l'élément transféré et l'état de l'indicateur de direction. EDI est incrémenté si DF avait été mis à 0 avec CLD ou décrémenté si DF avait été mis à 1 avec STD. Avec la forme STOS de l'instruction, un opérande doit être fourni pour indiquer la taille des éléments à copier. La dérogation de segment n'est pas permise. Lorsque l'une des formes STOSB (octets), STOSW (mots) ou STOSD (doubles mots) est utilisée, c'est le choix d'instruction qui détermine la taille des éléments de données à traiter et si l'élément provient de AL, AX ou EAX. @Pierre Marchand, 2002 92

Écrire une chaîne (la suite) STOS/STOSB/STOSW/STOSD Store String Data STOS et ses variantes sont souvent utilisées avec le préfixe REP pour remplir une chaîne avec une même valeur. Avant d'utiliser l'instruction REP, ECX doit contenir la nombre d'itérations désiré. oszapc = oszapc stos word ptr [edi] stosb rep stosw stosd @Pierre Marchand, 2002 93

Déplacer une chaînes ou un tableaux MOVS/MOVSB/MOVSW/MOVSDMove String Data Déplace une chaîne de données d’une région de la mémoire à une autre. esi doit pointer vers la chaîne source et edi vers la chaîne destination. Pour chaque élément déplacé, edi et esi sont ajustés selon la taille des opérandes et le bit de direction DF. Dans le cas de movs, il faut fournir des opérandes pour indiquer la taille des éléments à traiter. Ces instructions sont habituellement utilisées avec le préfixe rep. oszapc = oszapc rep movsb 1 movs word ptr [dest], word ptr [source]1 @Pierre Marchand, 2002 94

Exemple 02 L’exemple 02 contient différentes fonctions de traitement de chaînes de caractères et de tableaux démontrant l’utilisation des instruction que nous venons de voire. @Pierre Marchand, 2002 95

switch ( i ) { case 1: case 2: default: } switch: case 1: cmp … jne … … break; … … jmp … case 2: cmp break; jne … … … jmp default: … endswitch: @Pierre Marchand, 2002 i, 1 case 2 endswitch i, 2 default endswitch … 96

Optimisation des switch Dans les systèmes à base de menus, il arrive souvent qu’on ait un énoncé switch comme le suivant, où une fonction différente est exécutée suivant le choix que l’utilisateur fait dans un menu : switch (choix) { case 0: fonction 1(choix); break; case 1: fonction 2(choix); break; case 1: fonction 3(choix); } @Pierre Marchand, 2002 97

Tables de fonctions en C En C, on peut obtenir une meilleure performance, surtout si la liste est longue, à l’aide d’une table de pointeurs de fonctions : void (* mes. Fonctions [3] ) ( int ) = { fonction 1, fonction 2, fonction 3 }; ou int (* mes. Fonctions [3] ) ( int ) = { fonction 1, fonction 2, fonction 3 }; Ensuite, on peut appeler une de ces fonctions comme suit : (* mes. Fonctions [choix] ) ( param ); On saute directement à la bonne fonction sans avoir à parcourir le switch. @Pierre Marchand, 2002 98

Tables de fonctions en assembleur Dans le contexte C, nous pouvons accéder à ces fonctions en assembleur comme suit : … lea eax, mes. Fonctions mov ecx, choix mov ebx, param push ebx call [eax+ecx*4] // * 4 car pointeur = 32 bits add esp, 4. . . @Pierre Marchand, 2002 99

Exemple 03 L’exemple 03 montre différentes implantation d’un même « switch » @Pierre Marchand, 2002 100

Move conditionnel CMOVCC La famille d’instructions cmovcc permet d’éviter les branchements dans des instructions C telles que : x = (a > b) ? 1 : -1; mov eax, a mov ebx, b cmp eax, ebx mov eax, 1 mov edx, -1 cmovle eax, edx// si a > b, eax contient 1 // sinon, eax contient -1 @Pierre Marchand, 2002 101

Move conditionnel (la suite) CMOVCC L’instruction cmovcc est disponible avec toutes les conditions booléennes usuelles : cmovg reg, reg cmovg reg, mem cmovge reg, reg cmovge reg, mem cmovlreg, reg cmovlreg, mem cmovle reg, reg cmovle reg, mem etc. @Pierre Marchand, 2002 102

Instructions logiques @Pierre Marchand, 2002 103

Instructions and – or - xor AND/OR/XOR Logical AND/OR/XOR Effectue une opération logique bit par bit entre l’opérande source et l’opérande destination et enregistre le résultat dans la destination. oszapc = 0± ±? ± 0 and reg, reg 0, 5 or mem, reg xor reg, mem and reg, immed or mem, immed @Pierre Marchand, 2002 104

Instruction not NOT One ’s complement negation Effectue le complément logique (complément à 1) de chaque bit de la destination. oszapc = oszapc not reg 0, 5 not mem @Pierre Marchand, 2002 105

Instruction test TEST Teste les bits indiqués d’un opérande et positionne les indicateurs. L’un des opérandes contient la valeur à tester. L’autre contient un masque indiquant les bits à tester. L’instruction fait le AND de la source et de la destination. Les indicateurs sont modifiés en conséquence, mais la destination n’est pas changée. oszapc = 0 ± ± ? ± 0 test reg, reg 0, 5 test mem, reg test reg, mem test reg, immed test mem, immed @Pierre Marchand, 2002 106

Instruction rol - ror ROL/ROR Rotate Effectue une rotation de l ’opérande destination vers la gauche ou vers la droite du nombre de bits spécifié dans l ’opérande source. Le dernier bit décalé va également dans CF. oszapc = ±szap ± C ROL ROR ror ror C reg, 1 rol reg, CL rol mem, CL mem, immed @Pierre Marchand, 2002 reg, 1 reg, CL rol mem, immed 107

Instructions rcl - rcr RCL/RCR Rotate Effectue une rotation de l’opérande destination vers la gauche ou vers la droite du nombre de bits spécifié dans l’opérande source. Cette rotation inclut le bit CF, de sorte qu’une rotation sur 9 bits est effectuée sur un registre de 8 bits, sur 17 bits pour un registre de 16 bits ou sur 33 bits pour un registre de 32 bits. oszapc = ±szap ± C C @Pierre Marchand, 2002 108

Instructions rcl – rcr (la suite) RCL/RCR rcl rcr Rotate reg, 1 mem, CL reg, immed mem, immed @Pierre Marchand, 2002 109

Instructions arithmétiques @Pierre Marchand, 2002 110

Instruction add ADD Additionne l’opérande source à l’opérande destination. oszapc = add reg, reg 0, 5 add mem, reg add reg, mem add reg, immed add mem, immed @Pierre Marchand, 2002 111

Instruction adc ADC Add with Carry Additionne l ’opérande source et la retenue (CF) à l’opérande destination. oszapc = adc reg, reg 8 adc mem, reg adc reg, mem adc reg, immed 6 adc mem, immed @Pierre Marchand, 2002 112

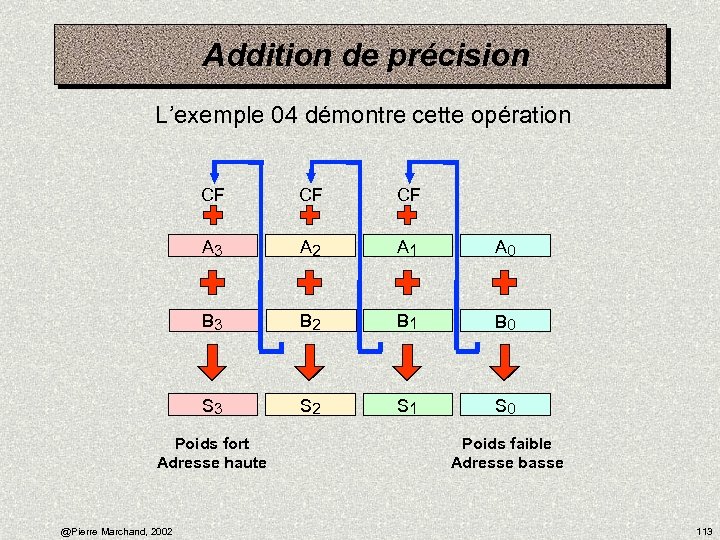Addition de précision L’exemple 04 démontre cette opération CF CF CF A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 S 3 S 2 S 1 S 0 Poids fort Adresse haute @Pierre Marchand, 2002 Poids faible Adresse basse 113

Instruction sub SUB Subtract Soustrait l’opérande source de l’opérande destination et stocke le résultat dans l’opérande destination. oszapc = ± ± ± sub reg, reg 0, 5 sub mem, reg sub reg, mem sub reg, immed sub mem, immed @Pierre Marchand, 2002 114

Instructions sbb SBB Subtract with borrow Ajoute l’indicateur CF au second opérande puis soustrait cette valeur du premier opérande. Le résultat est placé dans le premier opérande. oszapc = sbb reg, reg 8 sbb mem, reg sbb reg, mem sbb reg, immed 6 sbb mem, immed @Pierre Marchand, 2002 115

Multiplication Deux instructions : MUL pour la multiplication non signée IMUL pour la multiplication signée @Pierre Marchand, 2002 116

Multiplication signé et non signé Exemple: Supposons que eax = 0 x 80000001 eax peut être interprété comme: 2 147 483 649 (non signé) ou -2 147 483 647 (signé) Si ebx = 0 x 00000003, alors: mul ebx eax = 0 x 80000003 edx = 0 x 00000001 La réponse est le nombre 0 x 000000018000003, qui vaut 6 442 450 94710. @Pierre Marchand, 2002 117

Multiplication signé et non signé (la suite) Multiplication signée et non signée Mais : imul ebx eax = 0 x 80000003 edx= 0 x. FFFFFFFE et la réponse est le nombre $FFFFFFE 80000003, qui vaut -6 442 450 94110. Remarquez que dans les deux cas le double mot de poids faible est le même. @Pierre Marchand, 2002 118

Instructions mul MUL Unsigned Multiply Si l’opérande est de 32 bits, multiplie eax par l’opérande et place le résultat dans edx: eax et l’opérande sont considérés comme des quantités non signées. Si l’opérande est de 16 bits, multiplie ax par l’opérande et place le résultat dans dx: ax. Si l’opérande est de 8 bits, multiplie al par l’opérande et place le résultat dans ax. Les indicateurs OF et CF sont positionnés si la partie de poids fort du résultat n’est pas nulle. oszapc = ±? ? ± mul reg 14 -18 mul mem @Pierre Marchand, 2002 119

Instructions imul IMUL Signed Multiply Si l’opérande est de 32 bits, multiplie eax par l’opérande et place le résultat dans edx: eax et l ’opérande sont considérés comme des quantités signées. Si l’opérande est de 16 bits, multiplie ax par l’opérande et place le résultat dans dx: ax. Si l’opérande est de 8 bits, multiplie al par l’opérande et place le résultat dans ax. Les indicateurs OF et CF sont positionnés si le produit est étendu en signe dans edx pour des opérandes de 32 bits, dans dx pour des opérandes de 16 bits, ou dans ah pour des opérandes de 8 bits. oszapc = ±? ? ± imul reg 14 imul mem 15 -18 @Pierre Marchand, 2002 120

Intruction imul (la suite) IMUL Deux syntaxes supplémentaires depuis le 80386. Dans la version à deux opérandes, le registre destination est multiplié par l’opérande source et le résultat est placé dans le registre destination. Dans la version à trois opérandes, les deux derniers opérandes sont multipliés ensemble et le résultat est placé dans le registre destination. Les bits OF et CF sont positionnés si le produit n’entre pas dans la destination. imul reg, immed 14 imul reg, reg imul reg, mem imul reg, immed imul reg, mem, immed @Pierre Marchand, 2002 121

Grandeur des opérandes d’une multiplication Exemple 45 x 67 35 28 30 24 3015 Multiplication de deux nombres de 64 bits -> 128 bits XH YH @Pierre Marchand, 2002 XL YL 122

Multiplication de mots quadruples Composition du produit en additionnant les produits partiels de 64 bits + + + = XH YH XH YL XL YH XL YL Produit de 128 bits Exemple : long A[ ] = {0 x. FFFF, 0 x. FFFF}; long B[ ] = {0 x. FFFF, 0 x. FFFF}; long Produit[ ] = {0, 0, 0, 0}; @Pierre Marchand, 2002 123

Division signée et non signée Exemple: Supposons que eax = 0 x. FFFFFFF 8 eax peut être interprété comme: 4 294 967 28810 (non signé) ou -810 (signé) Si ebx = 0 x 00000003 et edx = 0 x 0000, alors: div ebx eax = 0 x 55555552 edx = 0 x 00000002 qui vaut 1 431 655 76210, reste 2. @Pierre Marchand, 2002 124

Division signé et non signé Division signée et non signée Mais si ebx = 0 x 00000003 et edx = 0 x. FFFF idiv ebx eax = 0 x. FFFFFFFE, edx = 0 x. FFFFFFFE qui vaut -210, reste -2. Par contre, si ebx = 0 x 00000003 et edx = 0 x. FFFF div ebx débordement de capacité parce que le quotient est > 32 bits. @Pierre Marchand, 2002 125

Division signé et non signé (la suite) Division signée et non signée Avant une division non signée, si le dividende dans eax est d’une longueur inférieure ou égale à 32 bits, il faut s’assurer que edx = 0. Avant une division signée, si le dividende est d’une longeur inférieure ou égale à 32 bits, il faut s’assurer que edx est 0 si eax est positif et 0 x. FFFF si eax est négatif. On peut effectuer ceci automatiquement avec l’instruction cdq, qui étend eax en signe sur 64 bits dans edx. mov eax, -597 mov ebx, 3 cdq idiv ebx @Pierre Marchand, 2002 126

Instruction div DIV Divide unsigned Si l’opérande est de 32 bits, divise eax par l’opérande et place le quotient dans eax et le reste dans edx. eax et l ’opérande sont considérés comme des quantités non signées. Si l’opérande est de 16 bits, divise dx: ax par l’opérande et place le quotient dans ax et le reste dans dx. Si l’opérande est de 8 bits, divise ax par l’opérande et place le quotient dans al et le reste dans ah. oszapc = ? ? ? div reg 56 -70 div mem @Pierre Marchand, 2002 127

Instruction idiv IDIV Signed Divide Si l’opérande est de 32 bits, divise eax par l’opérande et place le quotient dans eax et le reste dans edx. Les deux opérandes sont considérés comme des nombres signés. Si l’opérande est de 16 bits, divise dx: ax par l’opérande et place le quotient dans ax et le reste dans dx. Si l’opérande est de 8 bits, divise ax par l’opérande et place le quotient dans al et le reste dans ah. oszapc = ? ? ? idiv reg 56 -70 idiv mem @Pierre Marchand, 2002 128

Instructions sal - shl SAL SHL Shift arithmetic left Shift logical left Décale les bits de l’opérande destination vers la gauche le nombre de fois spécifié par l’opérande source. L’opérande source peut être cl ou une constante de 8 bits. OF est affecté seulement lors de décalages d’un bit. Dans les autres cas, il est indéfini. oszapc =±±±? ±± sal sal CF reg, 1 mem, 1 reg, CL mem, CL @Pierre Marchand, 2002 0 sal reg, immed 8 4 mem, immed 8 129

Instruction shr SHR Shift logical RIGHT Décale les bits de l’opérande destination vers la droite le nombre de fois spécifié par l’opérande source. L’opérande source peut être cl ou une constante de 8 bits. OF est affecté seulement lors de décalages d’un bit. Dans les autres cas, il est indéfini. oszapc =±±±? ±± shr shr shr 0 reg, 1 mem, 1 reg, CL mem, CL reg, immed 8 mem, immed 8 @Pierre Marchand, 2002 CF 4 130

Instruction sar SAR Shift arithmetic right Décale les bits de l’opérande destination vers la droite le nombre de fois spécifié par l’opérande source. L’opérande source peut être cl ou une constante de 8 bits. Le bit décalé à droite est placé dans CF tandis que le bit de gauche garde sa valeur. oszapc =±±±? ±± CF sar sar sar reg, 1 mem, 1 reg, CL mem, CL reg, immed 8 mem, immed 8 @Pierre Marchand, 2002 4 131

Instructions shld - shrd SHLD/SHRD Double Precision Shift Décale les bits du deuxième opérande dans le premier opérande. Le nombre de bits à décaler est spécifié par le troisième opérande. SHLD décale le premier opérande de n bits vers la gauche. Les positions laissées vacantes sont remplies par les n bits les plus significatifs du deuxième opérande. SHRD décale le premier opérande de n bits vers la droite. Les positions laissées vacantes sont remplies par les n bits les moins significatifs du deuxième opérande. @Pierre Marchand, 2002 132

Instructions shld – shrd (la suite) Le nombre de décalages peut être cl ou une constante de 8 bits. oszapc = ? ±± shld reg, immed 8 shld reg, CL shld mem, reg, immed 8 shld mem, reg, CL @Pierre Marchand, 2002 133

Division binaire 1 0 0 1 1 1 / 1 1 1 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 1 0 0 Donc Quotient = 0101 et Reste = 100 @Pierre Marchand, 2002 134

Division binaire (la suite) Division binaire Division (100111 / 111) sur 6 bits R Q Décalage no. 0 0 0 1 0 0 1 1 1 0 Q = 0 1 0 0 1 1 1 0 0 Q = 0 0 2 0 0 0 1 1 1 0 0 0 Q = 0 0 0 3 0 0 1 1 1 0 0 Q = 0 0 4 - 0 0 0 1 1 1 0 0 1 0 0 0 0 1 1 0 0 0 Q = 0 0 1 5 0 0 1 1 0 0 0 Q = 0 0 1 0 6 - 0 0 0 1 1 1 0 0 0 1 0 0 Q = 0 0 1 0 1 7 @Pierre Marchand, 2002 135

Division binaire (la suite) Division Principe R Q 1 si R ≥ D • • Pour plus de détails, voir le chapitre 1 du cours Structure Interne des ordinateurs. Initialement, R = 0 et Q = Dividende; D est le diviseur. On décale Q dans R un bit à la fois. Si R ≥ D, on effectue R = R - D et on passe 1 à droite du quotient, sinon on passe 0. On répète ceci autant de fois qu’il y a de bits dans le registre Q, par exemple, 16 ou 32 fois. @Pierre Marchand, 2002 136

Division binaire (la suite) Division • Finalement, on décale Q une dernière fois à gauche. • À la fin de l’opération, R contient le reste et Q le quotient. On peut effectuer cet algorithme sur des opérandes de plusieurs mots, par exemple Q = 64 bits et R = 64 bits, etc. @Pierre Marchand, 2002 137

Division de précision Division 128 bits par 64 bits Q R R+4 R D D+4 Q+12 Q+8 Q+4 Q 1 si R ≥ D D Pour effectuer cette opération, on a besoin des fonctionnalités suivantes (fonctions ou macros) : long. Shift. Left(src, dwords, shifts) long. Compare(dst, src, dwords) long. Sub(dst, src, dwords) @Pierre Marchand, 2002 138

Instructions neg NEG Negate Remplace l’opérande par son complément à 2. En fait, NEG effectue l’opération 0 - opérande. Si l ’opérande est 0, CF = 0, sinon CF = 1. Si l ’opérande contient -128 pour 8 bits, -32, 768 pour 16 bits ou - 2, 147, 483, 648 pour 32 bits, alors sa valeur ne change pas, mais OF et CF deviennent 1. oszapc = ± ± ± neg reg 0, 5 neg mem @Pierre Marchand, 2002 139