IERG 6120 Coding for distributed storage systems Kenneth Shum Sep 2016
Class logistics • Lecturer – Kenneth Shum – Office: SHB 736 • Venue – SHB 833 • Time – Tue 12: 30~13: 15 – Thr 11: 30~13: 00 Sep 2016 kshum 2
About me Engineering Mathematics Communications Nu alg mber eb rai theo c g ry eo me me try Computat ional Com ple NP-comp lete proble xity ms Computer Science
Class logistics • Enroll in Piazza. com – IERG 6120 Advanced topics in Information Engineering (Coding for Storage Systems) – Exercises and notes will be posted here. • Grading – Scribe notes (30%) – Programming project (30%) – Final Exam (40%) Sep 2016 kshum 4
Holidays • 20/9 Tue – Academic trip to Beijing • 11/10 Tue, 13/10 Thr – I will attend a conference for one week Sep 2016 kshum 5
Cloud Storage Sep 2016 kshum 6
Google’s data centers Data center at Singapore Sep 2016 kshum 7
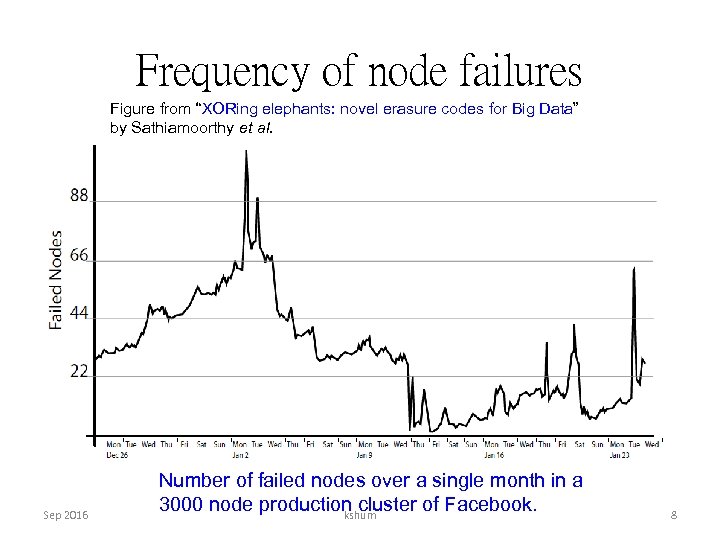
Frequency of node failures Figure from “XORing elephants: novel erasure codes for Big Data” by Sathiamoorthy et al. Sep 2016 Number of failed nodes over a single month in a 3000 node production cluster of Facebook. kshum 8
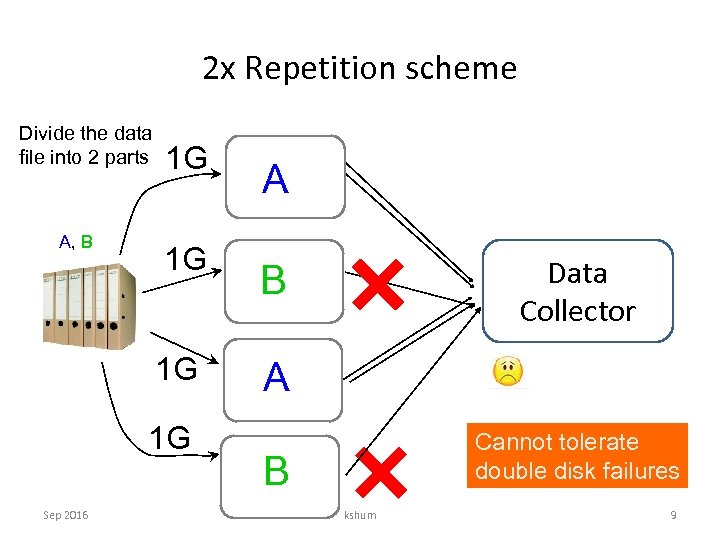
2 x Repetition scheme Divide the data file into 2 parts A, B 1 G 1 G Sep 2016 A Data Collector B A Cannot tolerate double disk failures B kshum 9
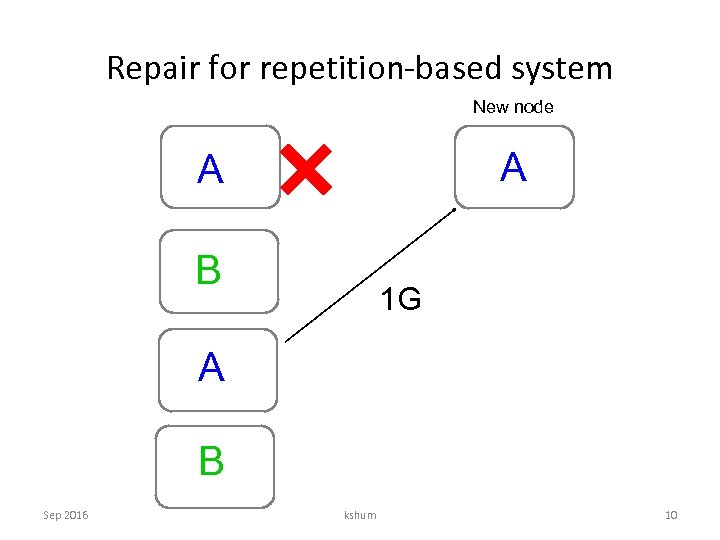
Repair for repetition-based system New node A A B 1 G A B Sep 2016 kshum 10
Performance metrics for repair • Locality – a. k. a. repair degree – The number of nodes contacted by the new node. • Repair bandwidth – The amount of data downloaded from the contacted nodes. Sep 2016 kshum 11
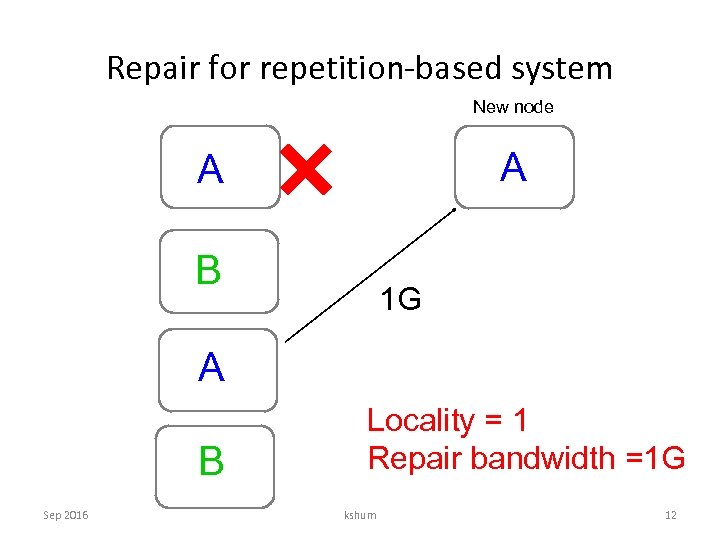
Repair for repetition-based system New node A A B 1 G A B Sep 2016 Locality = 1 Repair bandwidth =1 G kshum 12
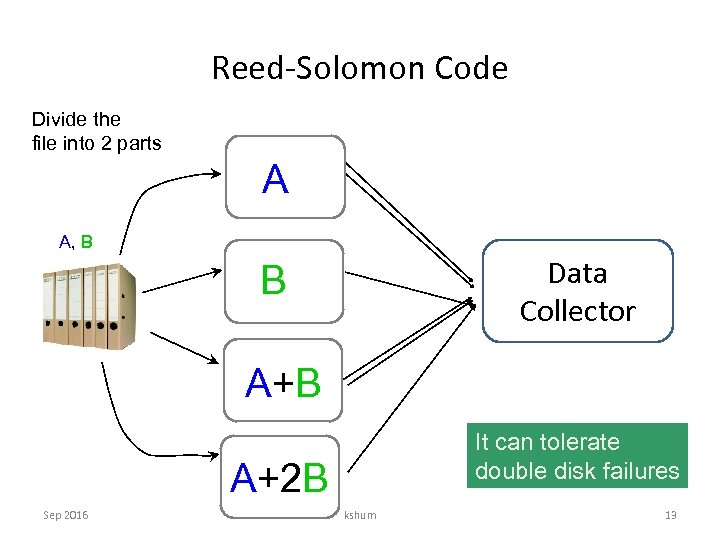
Reed-Solomon Code Divide the file into 2 parts A A, B Data Collector B A+B It can tolerate double disk failures A+2 B Sep 2016 kshum 13
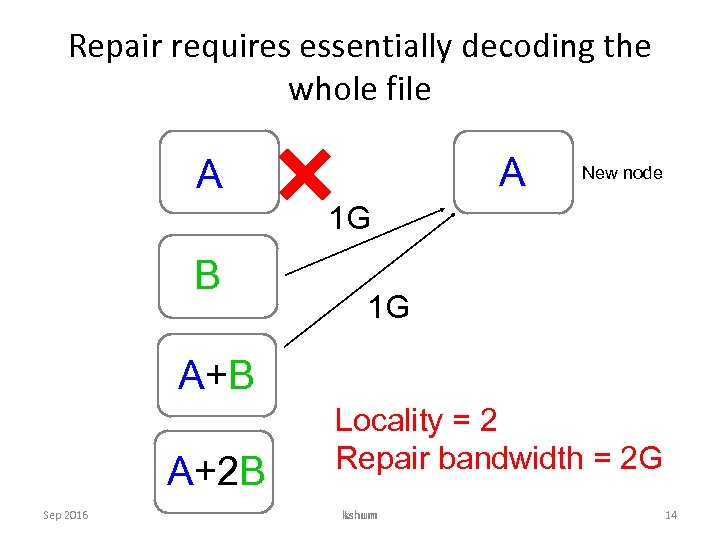
Repair requires essentially decoding the whole file A A New node 1 G B 1 G A+B A+2 B Sep 2016 Locality = 2 Repair bandwidth = 2 G kshum 14
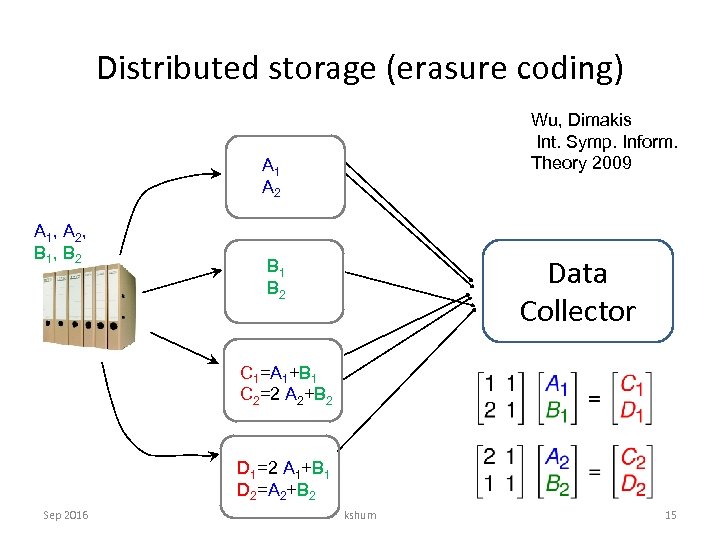
Distributed storage (erasure coding) Wu, Dimakis Int. Symp. Inform. Theory 2009 A 1 A 2 A 1, A 2, B 1, B 2 Data Collector B 1 B 2 C 1=A 1+B 1 C 2=2 A 2+B 2 D 1=2 A 1+B 1 D 2=A 2+B 2 Sep 2016 kshum 15
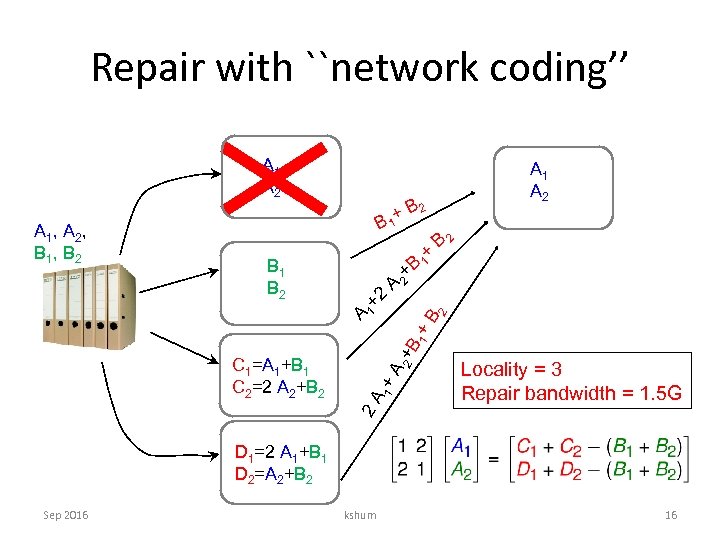
Repair with ``network coding’’ A 1 A 2 + B 2 B 1 + A 1+ 2 A C 1=A 1+B 1 C 2=2 A 2+B 2 2 +B 1+ A +2 1 A 2 2 B 1 B 2 B A 1, A 2, B 1, B 2 A 1 A 2 Locality = 3 Repair bandwidth = 1. 5 G D 1=2 A 1+B 1 D 2=A 2+B 2 Sep 2016 kshum 16
Comparison of the three examples Repetition scheme Reed-Solomon Codes Regenerating codes Storage efficiency 1/2 1/2 Reliability Tolerate one disk failure Tolerate two disk failures Repair bandwidth 1 G 2 G 1. 5 G Locality 1 2 3 Sep 2016 kshum 17
Course content • Basic coding theory – Finite field – Reed-Solomon code • Locally repairable code – Codes with small locality • Regenerating code – Codes with small repair bandwidth • Codes for FLASH memory Sep 2016 kshum 18
References on coding theory • E. R. Berlekamp, “Algebraic coding theory, ” World Scientific Publishing, 1968. • F. J. Mac. Williams and N. J. A. Sloane, “The theory of error-correcting codes, ” North Holland, 1977. • J. H. van Lint, “Introduction to coding theory, ” 3 rd edition, Springer-Verlag, 1999. • R. Roth, “Introduction to coding theory, ” Cambridge University Press, 2006. Sep 2016 kshum 19
References on storage codes • F. Oggier and A. Datta, “Coding techniques for repairability in networked distributed storage, ” NOW publisher, 2013. • A. Barg and I. Tamo, “Theory and practice of codes with locality, ” tutorial notes, IEEE Int. Symp. on Information Theory, 2016. • L. Dolecek, “Channel coding methods for nonvolatile memories, ” NOW publisher, 2016. Sep 2016 kshum 20
Скачать презентацию IERG 6120 Coding for distributed storage systems Kenneth
561e22e6c62759a15604aae4d868d7ee.ppt