ier Bio/Chemical Kinetics Made Easy A Numerical Approach Petr Kuzmič, Ph. D. Bio. Kin, Ltd. 1. Case study: Inhibition of LF protease from B. anthracis 2. Method: Numerical Enzyme Kinetics Bio/Chemical Kinetics Made Easy
Anthrax bacillus CUTANEOUS AND INHALATION ANTHRAX DISEASE Bio/Chemical Kinetics Made Easy 2
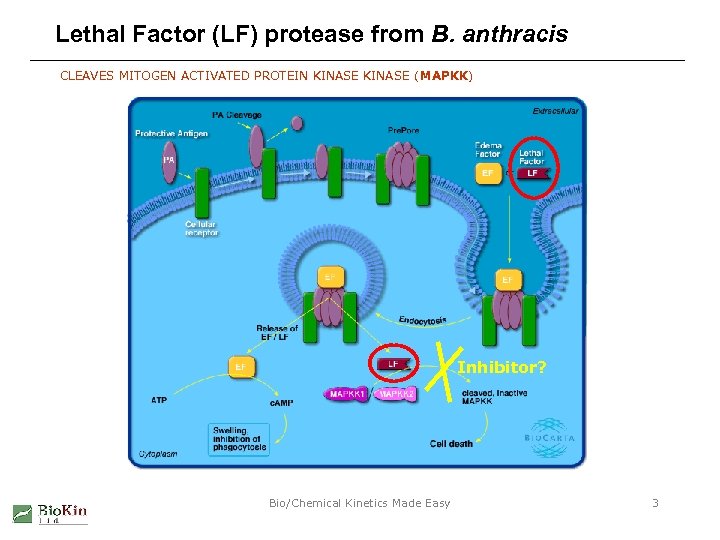
Lethal Factor (LF) protease from B. anthracis CLEAVES MITOGEN ACTIVATED PROTEIN KINASE (MAPKK) Inhibitor? Bio/Chemical Kinetics Made Easy 3
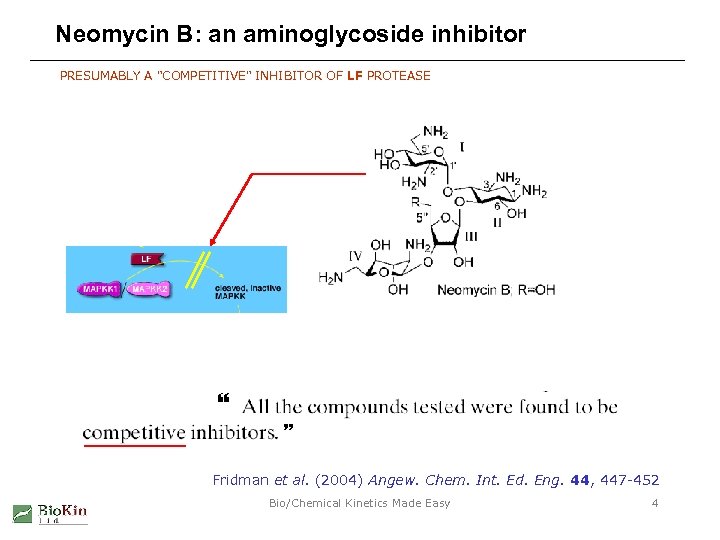
Neomycin B: an aminoglycoside inhibitor PRESUMABLY A "COMPETITIVE" INHIBITOR OF LF PROTEASE Fridman et al. (2004) Angew. Chem. Int. Ed. Eng. 44, 447 -452 Bio/Chemical Kinetics Made Easy 4
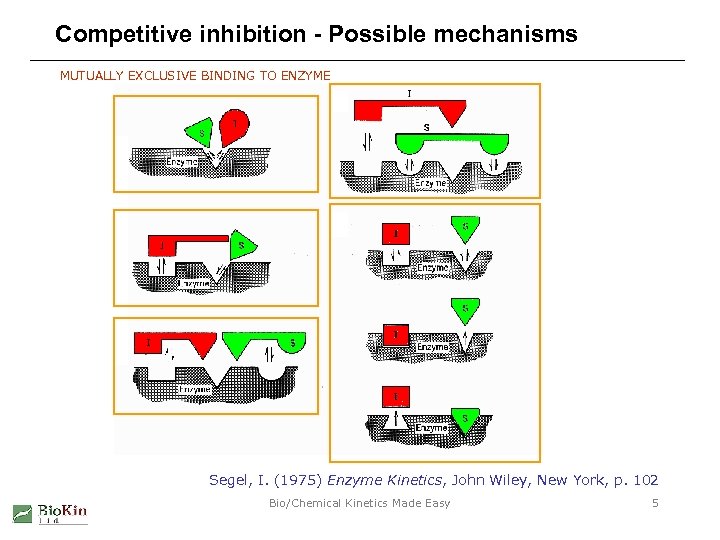
Competitive inhibition - Possible mechanisms MUTUALLY EXCLUSIVE BINDING TO ENZYME Segel, I. (1975) Enzyme Kinetics, John Wiley, New York, p. 102 Bio/Chemical Kinetics Made Easy 5
![Competitive inhibition - Kinetics AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS COMPLETELY RESTORED same](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-6.jpg "Competitive inhibition - Kinetics AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS COMPLETELY RESTORED same")
Competitive inhibition - Kinetics AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS COMPLETELY RESTORED same V ! increase [I] Bio/Chemical Kinetics Made Easy 6
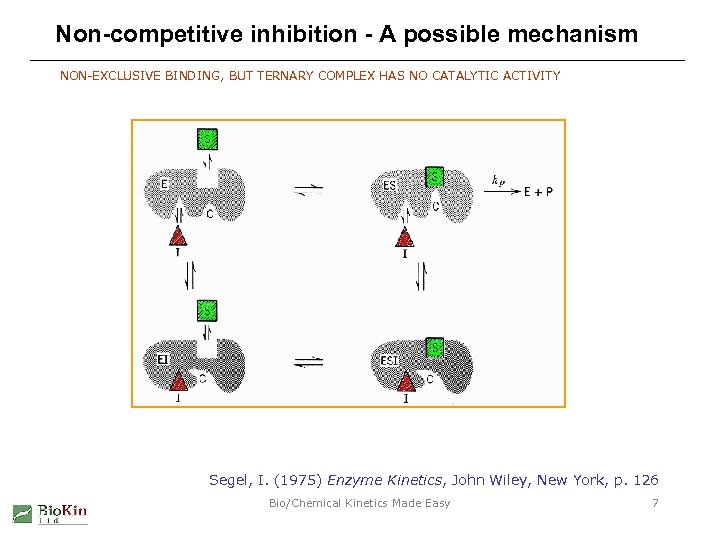
Non-competitive inhibition - A possible mechanism NON-EXCLUSIVE BINDING, BUT TERNARY COMPLEX HAS NO CATALYTIC ACTIVITY Segel, I. (1975) Enzyme Kinetics, John Wiley, New York, p. 126 Bio/Chemical Kinetics Made Easy 7
![Non-competitive inhibition - Kinetics EVEN AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS NEVER FULLY](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-8.jpg "Non-competitive inhibition - Kinetics EVEN AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS NEVER FULLY")
Non-competitive inhibition - Kinetics EVEN AT VERY HIGH [SUBSTRATE], ANZYME ACTIVITY IS NEVER FULLY RESTORED increase [I] Bio/Chemical Kinetics Made Easy 8
![Compare saturation curves DIAGNOSIS OF MECHANISMS: SAME OR DIFFERENT RATE AT VERY LARGE [S]?](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-9.jpg "Compare saturation curves DIAGNOSIS OF MECHANISMS: SAME OR DIFFERENT RATE AT VERY LARGE [S]?")
Compare saturation curves DIAGNOSIS OF MECHANISMS: SAME OR DIFFERENT RATE AT VERY LARGE [S]? COMPETITIVE NON-COMPETITIVE ? Bio/Chemical Kinetics Made Easy 9
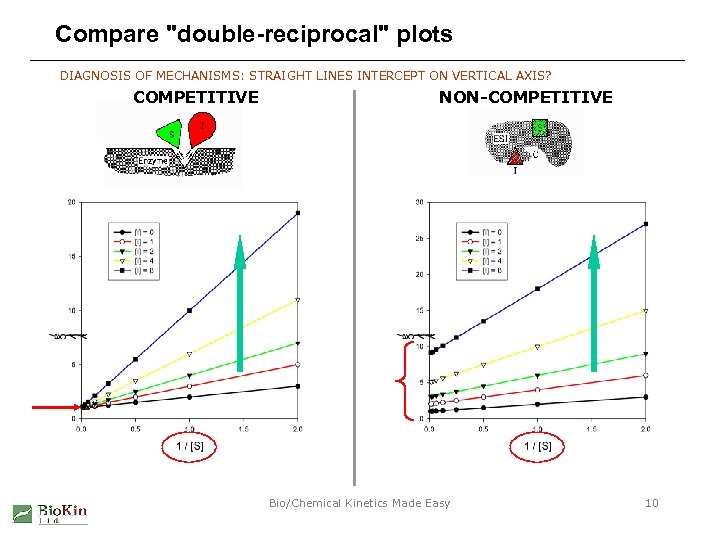
Compare "double-reciprocal" plots DIAGNOSIS OF MECHANISMS: STRAIGHT LINES INTERCEPT ON VERTICAL AXIS? COMPETITIVE NON-COMPETITIVE Bio/Chemical Kinetics Made Easy 10
Traditional plan to determine inhibition mechanism THE TRADITIONAL APPROACH 1. Measure enzyme activity at increasing [S] Collect multiple substrate-saturation curves at varied [I] 2. Convert [S] vs. activity data to double-reciprocal coordinates 3. Perform a linear fit of transformed (double-reciprocal) data 4. Check if resulting straight lines intersect on the vertical axis If yes, declare the inhibition mechanism competitive Fridman et al. (2004) Angew. Chem. Int. Ed. Eng. 44, 447 -452 Bio/Chemical Kinetics Made Easy 11
![Collect experimental data at varied [S] and [I] THE RAW DATA [I] = 0.](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-12.jpg "Collect experimental data at varied [S] and [I] THE RAW DATA [I] = 0.")
Collect experimental data at varied [S] and [I] THE RAW DATA [I] = 0. 5 m. M [I] = 1. 0 m. M [I] = 2. 0 m. M Bio/Chemical Kinetics Made Easy 12
![Check for intersection of double-reciprocal plots DO LINEWEAVER-BURK PLOTS INTERSECT? [I] = 0. 5](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-13.jpg "Check for intersection of double-reciprocal plots DO LINEWEAVER-BURK PLOTS INTERSECT? [I] = 0. 5")
Check for intersection of double-reciprocal plots DO LINEWEAVER-BURK PLOTS INTERSECT? [I] = 0. 5 m. M [I] = 1. 0 m. M [I] = 2. 0 m. M COMPETITIVE Bio/Chemical Kinetics Made Easy 13
![Doubts begin to appear. . . IS THIS A STRAIGHT LINE? [I] = 0](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-14.jpg "Doubts begin to appear. . . IS THIS A STRAIGHT LINE? [I] = 0")
Doubts begin to appear. . . IS THIS A STRAIGHT LINE? [I] = 0 Bio/Chemical Kinetics Made Easy 14
Mysterious substrate saturation data MICHAELIS-MENTEN KINETICS IS NOT SUPPOSED TO SHOW A MAXIMUM ! [I] = 0 Throw these out? Bio/Chemical Kinetics Made Easy 15
![Repeat substrate experiment at higher [S] SEE IF MAXIMUM HOLDS UP AT HIGHER [S]](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-16.jpg "Repeat substrate experiment at higher [S] SEE IF MAXIMUM HOLDS UP AT HIGHER [S]")
Repeat substrate experiment at higher [S] SEE IF MAXIMUM HOLDS UP AT HIGHER [S] [I] = 0 Bio/Chemical Kinetics Made Easy 16
Substrate inhibition in LF protease is real HAS ANYONE ELSE SEEN IT? Tonello et al. (2003) J. Biol. Chem. 278, 40075 -78. Bio/Chemical Kinetics Made Easy 17
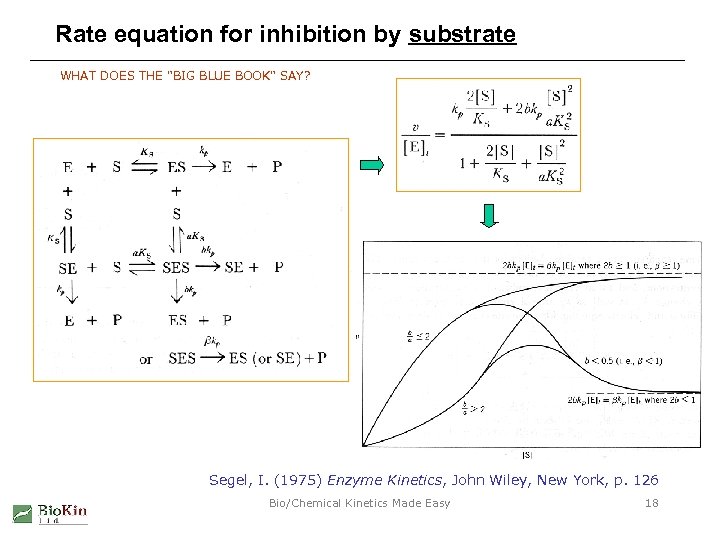
Rate equation for inhibition by substrate WHAT DOES THE "BIG BLUE BOOK" SAY? Segel, I. (1975) Enzyme Kinetics, John Wiley, New York, p. 126 Bio/Chemical Kinetics Made Easy 18
Rate equation for inhibition by substrate + inhibitor WHAT DOES THE "BIG BLUE BOOK" SAY? ? Bio/Chemical Kinetics Made Easy 19
ier Bio/Chemical Kinetics Made Easy A Numerical Approach Petr Kuzmič, Ph. D. Bio. Kin, Ltd. 1. Case study: Inhibition LF protease from B. anthracis 2. Method: Numerical Enzyme Kinetics Bio/Chemical Kinetics Made Easy
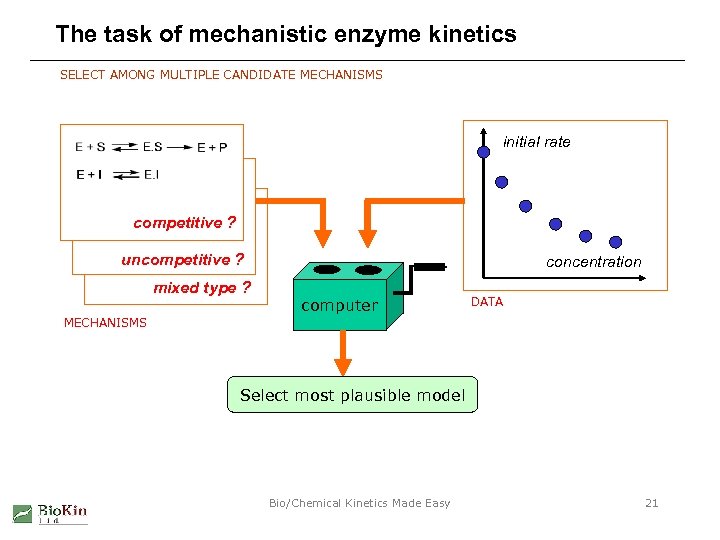
The task of mechanistic enzyme kinetics SELECT AMONG MULTIPLE CANDIDATE MECHANISMS initial rate competitive ? uncompetitive ? mixed type ? concentration computer DATA MECHANISMS Select most plausible model Bio/Chemical Kinetics Made Easy 21
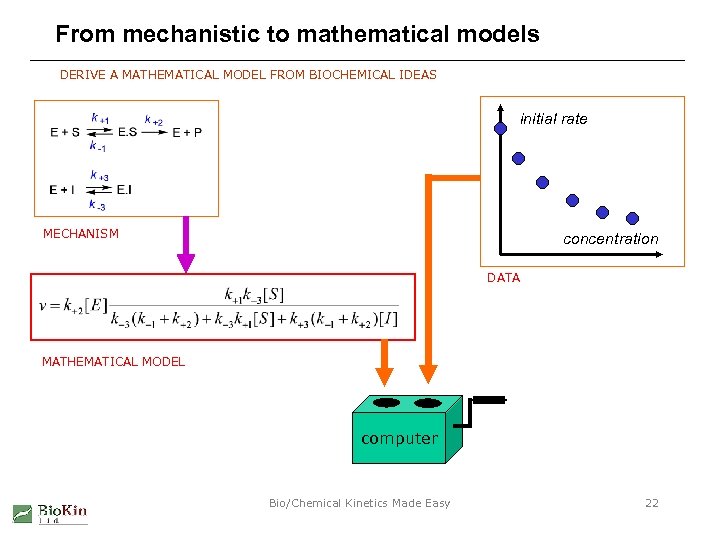
From mechanistic to mathematical models DERIVE A MATHEMATICAL MODEL FROM BIOCHEMICAL IDEAS initial rate MECHANISM concentration DATA MATHEMATICAL MODEL computer Bio/Chemical Kinetics Made Easy 22
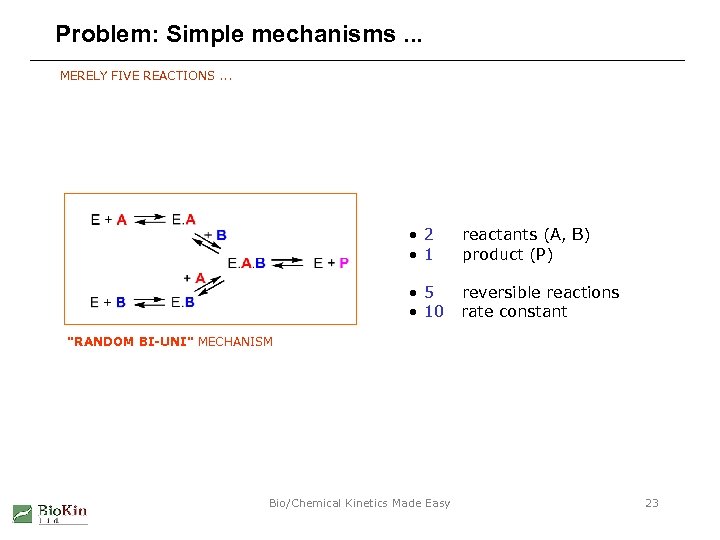
Problem: Simple mechanisms. . . MERELY FIVE REACTIONS. . . • 2 • 1 reactants (A, B) product (P) • 5 • 10 reversible reactions rate constant "RANDOM BI-UNI" MECHANISM Bio/Chemical Kinetics Made Easy 23
. . . lead to complex algebraic models MERELY FIVE REACTIONS. . . Segel, I. (1975) Enzyme Kinetics. John Wiley, New York, p. 646. "RANDOM BI-UNI" MECHANISM Bio/Chemical Kinetics Made Easy 24
A solution: Forget about algebra POSSIBLE STRATEGY FOR MECHANISTIC MODEL BUILDING • Do not even try to derive complex algebraic equations • Instead, derive systems of simple, simultaneous equations • Solve these systems using numerical methods Bio/Chemical Kinetics Made Easy 25
Theoretical foundations: Mass Action Law RATE IS PROPORTIONAL TO CONCENTRATION(S) “rate” … “derivative” MONOMOLECULAR REACTIONS rate is proportional to [A] - d [A] / d t = k [A] monomolecular rate constant 1 / time BIMOLECULAR REACTIONS rate is proportional to [A] [B] - d [A] / d t = - d [B] / d t = k [A] [B] bimolecular rate constant 1 / (concentration time) Bio/Chemical Kinetics Made Easy 26
Theoretical foundations: Mass Conservation Law PRODUCTS ARE FORMED WITH THE SAME RATE AS REACTANTS DISAPPEAR EXAMPLE - d [A] / d t = + d [P] / d t = + d [Q] / d t COMPOSITION RULE ADDITIVITY OF TERMS FROM SEPARATE REACTIONS mechanism: d [B] / d t = + k 1 [A] - k 2 [B] Bio/Chemical Kinetics Made Easy 27
![Composition Rule: Example EXAMPLE MECHANISM RATE EQUATIONS d[P] / d t = + k+5](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-28.jpg "Composition Rule: Example EXAMPLE MECHANISM RATE EQUATIONS d[P] / d t = + k+5")
Composition Rule: Example EXAMPLE MECHANISM RATE EQUATIONS d[P] / d t = + k+5 [EAB] d[EAB] / d t = + k+2 [EA] [B] - k-2 [EAB] + k+4 [EB] [A] - k-4 [EAB] - k+5 [EAB] Similarly for other species. . . Bio/Chemical Kinetics Made Easy 28
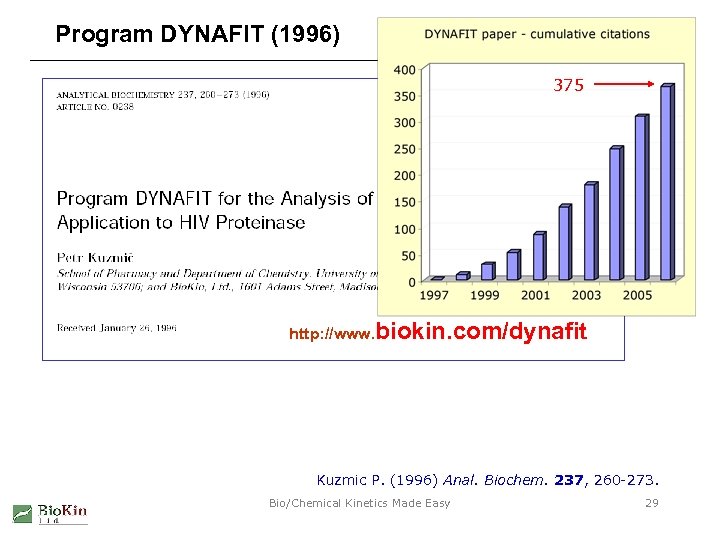
Program DYNAFIT (1996) 375 http: //www. biokin. com/dynafit Kuzmic P. (1996) Anal. Biochem. 237, 260 -273. Bio/Chemical Kinetics Made Easy 29
A "Kinetic Compiler" HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 [ES] Rate equations: d[E ] / dt = - k 1 [E] [S] + k 2 [ES] + k 3 [ES] d[ES ] / dt = + k 1 [E] [S] - k 2 [ES] - k 3 [ES] Similarly for other species. . . Bio/Chemical Kinetics Made Easy 30
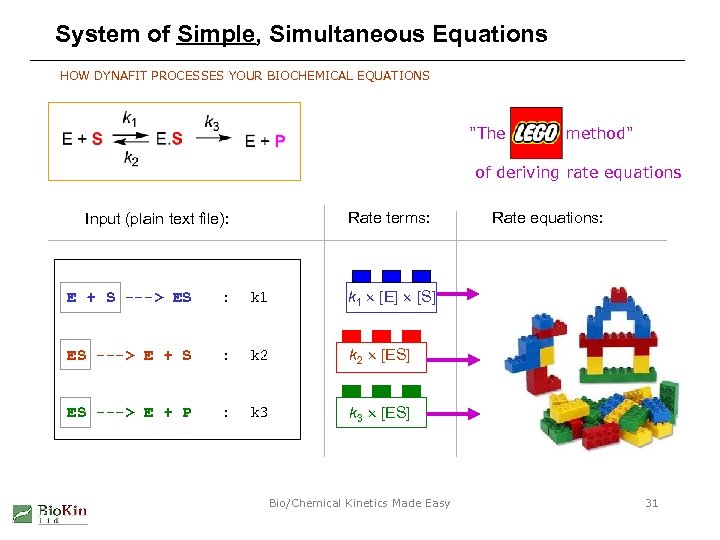
System of Simple, Simultaneous Equations HOW DYNAFIT PROCESSES YOUR BIOCHEMICAL EQUATIONS "The LEGO method" of deriving rate equations Rate terms: Input (plain text file): E + S ---> ES : k 1 [E] [S] ES ---> E + S : k 2 [ES] ES ---> E + P : k 3 Rate equations: k 3 [ES] Bio/Chemical Kinetics Made Easy 31
Initial rate kinetics TWO BASIC APPROXIMATIONS 1. Rapid-Equilibrium Approximation assumed very much slower than k 1, k 2 2. Steady-State Approximation New in Dyna. Fit • no assumptions made about relative magnitude of k 1, k 2, k 3 • concentrations of enzyme forms are unchanging Bio/Chemical Kinetics Made Easy 32
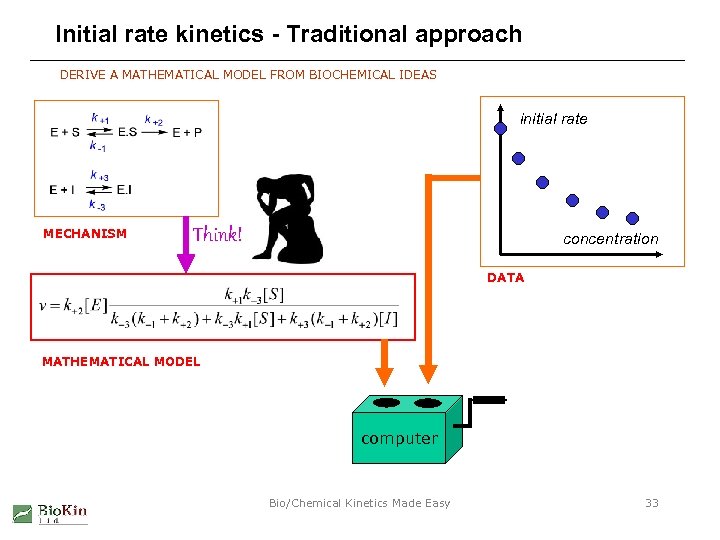
Initial rate kinetics - Traditional approach DERIVE A MATHEMATICAL MODEL FROM BIOCHEMICAL IDEAS initial rate MECHANISM Think! concentration DATA MATHEMATICAL MODEL computer Bio/Chemical Kinetics Made Easy 33
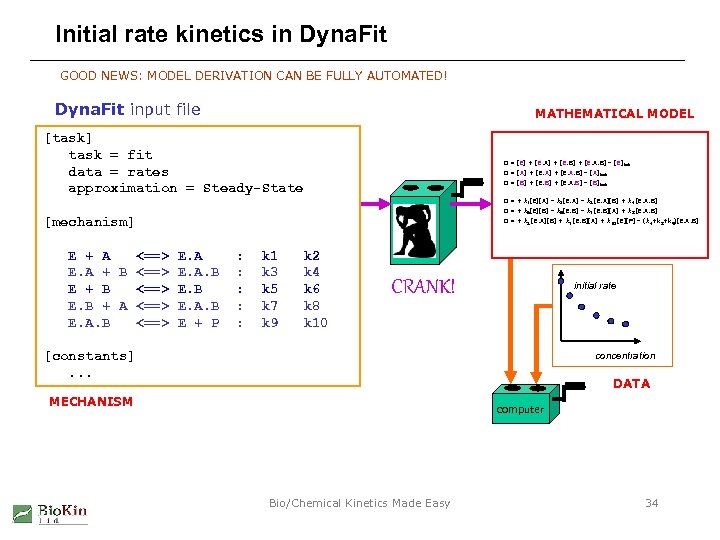
Initial rate kinetics in Dyna. Fit GOOD NEWS: MODEL DERIVATION CAN BE FULLY AUTOMATED! Dyna. Fit input file MATHEMATICAL MODEL [task] task = fit data = rates approximation = Steady-State 0 = [E] + [E. A] + [E. B] + [E. A. B] – [E]tot 0 = [A] + [E. A. B] – [A]tot 0 = [B] + [E. A. B] – [B]tot 0 = + k 1[E][A] – k 2[E. A] – k 3 [E. A][B] + k 4 [E. A. B] 0 = + k 5[E][B] – k 6[E. B] – k 7 [E. B][A] + k 8 [E. A. B] [mechanism] E + A <==> E. A + B <==> E. A. B E + B <==> E. B + A <==> E. A. B <==> E + P 0 = + k 3 [E. A][B] + k 7 [E. B][A] + k 10 [E][P] – (k 4+k 8+k 9)[E. A. B] : : : k 1 k 3 k 5 k 7 k 9 k 2 k 4 k 6 k 8 k 10 CRANK! initial rate [constants]. . . concentration DATA MECHANISM computer Bio/Chemical Kinetics Made Easy 34
Initial rate kinetics in Dyna. Fit vs. traditional method WHICH DO YOU LIKE BETTER? [task] task = fit data = rates approximation = Steady-State [reaction] A + B --> P [mechanism] E + A <==> E. A + B <==> E. A. B E + B <==> E. B + A <==> E. A. B <==> E + P : : : k 1 k 3 k 5 k 7 k 9 k 2 k 4 k 6 k 8 k 10 [constants]. . . [concentrations]. . . Bio/Chemical Kinetics Made Easy 35
ier Bio/Chemical Kinetics Made Easy A Numerical Approach Petr Kuzmič, Ph. D. Bio. Kin, Ltd. 1. Case study: Inhibition LF protease from B. anthracis 2. Method: Numerical Enzyme Kinetics Bio/Chemical Kinetics Made Easy
![Dyna. Fit model for inhibition by substrate ENZYME KINETICS MADE EASIER [reaction] [enzyme] [modifiers]](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-37.jpg "Dyna. Fit model for inhibition by substrate ENZYME KINETICS MADE EASIER [reaction] [enzyme] [modifiers]")
Dyna. Fit model for inhibition by substrate ENZYME KINETICS MADE EASIER [reaction] [enzyme] [modifiers] | | | S ---> P E I [mechanism] E + S <===> E. S. S E. S ---> E + P : : : Ks Ks 2 kcat dissociation . . . Bio/Chemical Kinetics Made Easy 37
![Dyna. Fit model for inhibition by substrate + inhibitor ENZYME KINETICS MADE EASIER [reaction]](https://present5.com/presentation/d5510ccfc92f156f70927f9a15cd4ef6/image-38.jpg "Dyna. Fit model for inhibition by substrate + inhibitor ENZYME KINETICS MADE EASIER [reaction]")
Dyna. Fit model for inhibition by substrate + inhibitor ENZYME KINETICS MADE EASIER [reaction] [enzyme] [modifiers] | | | S ---> P E I [mechanism] E + E. S S <===> E. S + S <===> E. S. S ---> E + P I <===> E. I + I <===> E. S. I : : : Ks Ks 2 kcat Ki Kis dissoc [constants] Ks = 1 ? , Ks 2 = 1 ? , kcat = 1 ? Ki = 1 ? , Kis = 1 ? optimization flag . . . initial estimate Bio/Chemical Kinetics Made Easy 38
How do we know which mechanism is "best"? COMPARE ANY NUMBER OF MODELS IN A SINGLE RUN [task] task = fit | data = rates model = mixed-type ? [reaction] [enzyme] [modifiers] | | | S ---> P E I . . . [task] task = fit | data = rates model = competitive ? . . . [task] task = fit | data = rates model = uncompetitive ? . . . Akaike Information Criterion Review: Burnham & Anderson (2004) Bio/Chemical Kinetics Made Easy 39
The best model: mixed-type noncompetitive NEOMYCIN B IS NOT A COMPETITIVE INHBITOR OF LETHAL FACTOR PROTEASE Kuzmic et al. (2006) FEBS J. 273, 3054 -3062. Bio/Chemical Kinetics Made Easy 40
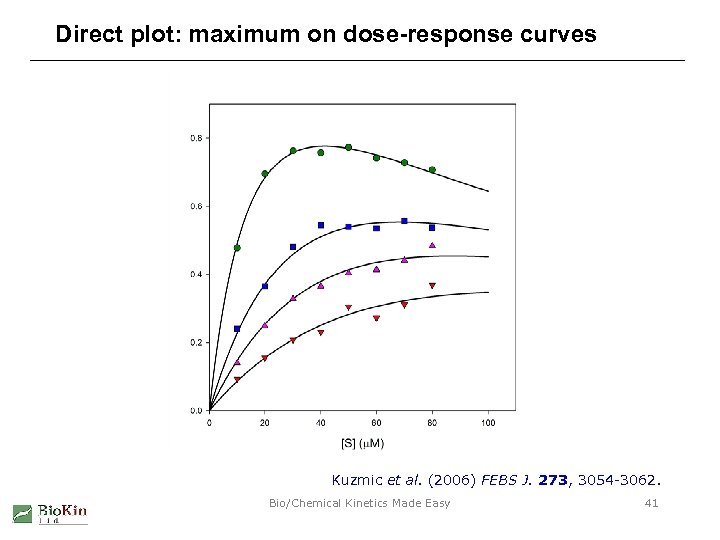
Direct plot: maximum on dose-response curves Kuzmic et al. (2006) FEBS J. 273, 3054 -3062. Bio/Chemical Kinetics Made Easy 41
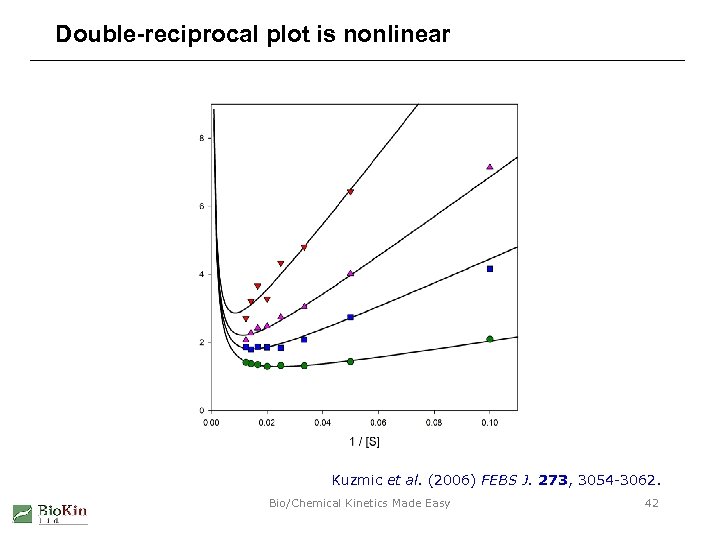
Double-reciprocal plot is nonlinear Kuzmic et al. (2006) FEBS J. 273, 3054 -3062. Bio/Chemical Kinetics Made Easy 42
DR plot obscures deviations from the model Kuzmic et al. (2006) FEBS J. 273, 3054 -3062. Bio/Chemical Kinetics Made Easy 43
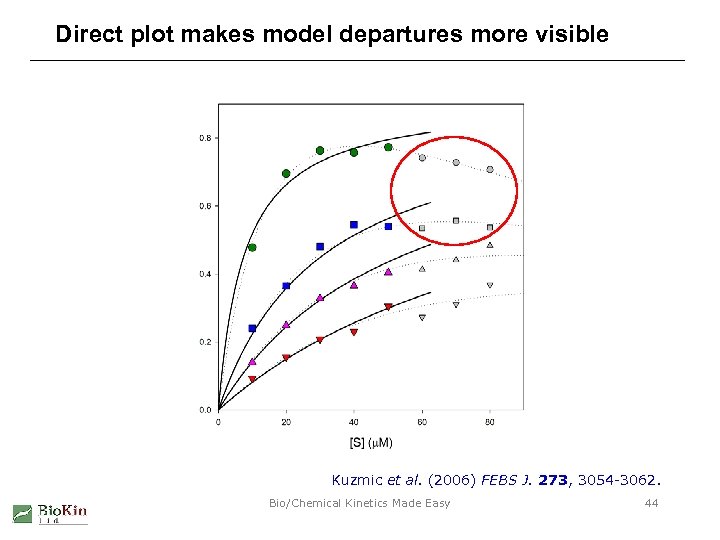
Direct plot makes model departures more visible Kuzmic et al. (2006) FEBS J. 273, 3054 -3062. Bio/Chemical Kinetics Made Easy 44
Summary: Enzyme kinetics made (almost) easy HOW DO I BUILD A MATHEMATICAL MODEL FOR AN ENZYME MECHANISM? • Let the computer derive your model - don't bother with algebra. • For many important mechanisms, algebraic models don't exist anyway. • The theoretical foundation is simple and well understood: - mass action law - mass conservation law • The same set of -like rules apply to all types of kinetic models: - reaction progress curves - initial reaction rates Bio/Chemical Kinetics Made Easy 45
Acknowledgements: Lethal Factor protease work Hawaii Biotech currently Panthera Bio. Pharma National Institutes of Health Grant No. R 43 AI 52587 -02 U. S. Army Medical Research and Materials Command Contract No. V 549 P-6073 Mark Goldman Sheri Millis Lynne Cregar Aiea, Island of Oahu, Hawaii Bio/Chemical Kinetics Made Easy 46
Скачать презентацию ier Bio Chemical Kinetics Made Easy A Numerical Approach
d5510ccfc92f156f70927f9a15cd4ef6.ppt