c8731abc47bcaddcf1cc1e11f3175ffb.ppt
- Количество слайдов: 43

IE 531 Linear Programming Spring 2010 박성수 Linear Programming 2010 1

Course Objectives q Why need to study LP? Ø Important tool by itself Ø Theoretical basis for later developments (IP, Network, Graph, Nonlinear, scheduling, Sets, Coding, Game, … ) Ø Formulation + package is not enough for advanced applications and interpretation of results q Objectives of the class: Ø Understand theory of linear optimization Ø Preparation for more in-depth optimization theory Ø Modeling capabilities Ø Introduction to use of software (Xpress-MP and/or CPLEX) Linear Programming 2010 2

q Prerequisite: basic linear algebra/calculus, earlier exposure to LP/OR helpful, mathematical maturity (reading proofs, logical thinking) q Be steady in studying. Linear Programming 2010 3

Chapter 1 Introduction q Mathematical Programming Problem: min/max f(x) subject to gi(x) 0, i = 1, . . . , m, (hj(x) = 0, j = 1, . . . , k, ) ( x X Rn ) f, gi, hj : Rn R q If f, gi, hj linear (affine) function linear programming problem If f, gi, hj (or part of them) nonlinear function nonlinear programming problem If solution set restricted to be integer points integer programming problem Linear Programming 2010 4

q Linear programming: problem of optimizing (maximize or minimize) a linear (objective) function subject to linear inequality constraints. q General form: {max, min} c'x subject to ai'x bi , i M 1 ai'x bi , i M 2 ai'x = bi , i M 3 xj 0, j N 1 , xj 0, j N 2 c, ai , x Rn (There may exist variables unrestricted in sign) q inner product of two column vectors x, y Rn : x’y = i = 1 n xiyi If x’y = 0, x, y 0, then x, y are said to be orthogonal. In 3 -D, the angle between the two vectors is 90 degrees. ( vectors are column vectors unless specified otherwise) Linear Programming 2010 5

q Big difference from systems of linear equations is the existence of objective function and linear inequalities (instead of equalities) q Much deeper theoretical results and applicability than systems of linear equations. q x 1, x 2, …, xn : (decision) variables bi : right-hand-side ai'x { , , } bi : i th constraint xj { , } 0 : nonnegativity (nonpositivity) constraint c'x : objective function q Other terminology: feasible solution, feasible set (region), free (unrestricted) variable, optimal (feasible) solution, optimal cost, unbounded Linear Programming 2010 6

Important submatrix multiplications q Interpretation of constraints: A: m n , where ei is i-th unit vector denote constraints as Ax { , , } b Linear Programming 2010 7

q Any LP can be expressed as min c'x, Ax b max c'x min (-c'x) and take negative of the optimal cost ai'x bi -ai'x -bi ai'x = bi ai'x bi , -ai'x -bi nonnegativity (nonpositivity) are special cases of inequalities which will be handled separately in the algorithms. Feasible solution set of LP can always be expressed as Ax b (or Ax b) (called polyhedron, a set which can be described as a solution set of finitely many linear inequalities) q We may sometimes use max c'x, Ax b form (especially, when we study polyhedron) Linear Programming 2010 8

Brief History of LP (or Optimization) q Gauss: Gaussian elimination to solve systems of equations Fourier(early 19 C) and Motzkin(20 C) : solving systems of linear inequalities Farkas, Minkowski, Weyl, Caratheodory, … (19 -20 C): Mathematical structures related to LP (polyhedron, systems of alternatives, polarity) Kantorovich (1930 s) : efficient allocation of resources (Nobel prize in 1975 with Koopmans) Dantzig (1947) : Simplex method 1950 s : emergence of Network theory, Integer and combinatorial optimization, development of computer 1960 s : more developments 1970 s : disappointment, NP-completeness, more realistic expectations Khachian (1979) : ellipsoid method for LP Linear Programming 2010 9

1980 s : personal computer, easy access to data, willingness to use models Karmarkar (1984) : Interior point method 1990 s : improved theory and software, powerful computers software add-ins to spreadsheets, modeling languages, large scale optimization, more intermixing of O. R. and A. I. Markowitz (1990) : Nobel prize for portfolio selection (quadratic programming) Nash (1994) : Nobel prize for game theory 21 C (? ) : Lots of opportunities more accurate and timely data available more theoretical developments better software and computer need for more automated decision making for complex systems need for coordination for efficient use of resources (e. g. supply chain management, APS, traditional engineering problems, bio. . . ) Linear Programming 2010 10

Application Areas of Optimization q Operations Managements Production Planning Scheduling (production, personnel, . . ) Transportation Planning, Logistics Energy Military Finance Marketing E-business Telecommunications Games Engineering Optimization (mechanical, electrical, bioinformatics, . . . ) System Design … Linear Programming 2010 11

Resources q Societies: Ø INFORMS (the Institute for Operations Research and Management Sciences) : www. informs. org Ø MPS (The Mathematical Programming Society) : www. mathprog. org Ø Korean Institute of Industrial Engineers : kiie. org Ø Korean Operations Research Society : www. korms. or. kr q Journals: Operations Research, Management Science, Mathematical Programming, Networks, European Journal of Operational Research, Naval Research Logistics, Journal of the Operational Research Society, Interfaces, … Linear Programming 2010 12

Standard form problems q Standard form : min c'x, Ax = b, x 0 Ø Find optimal weights (nonnegative) from possible nonnegative linear combinations of columns of A to obtain b vector Ø Find optimal solution that satisfies linear equations and nonnegativity q Reduction to standard form Free (unrestricted) variable xj xj+ - xj- , xj+, xj- 0 j aijxij bi j aijxij + si = bi , si 0 (slack variable) j aijxij bi j aijxij - si = bi , si 0 (surplus variable) Linear Programming 2010 13

q Any (practical) algorithm can solve the LP problem in equality form only (except nonnegativity) q Modified form of the simplex method can solve the problem with free variables directly (w/o using difference of two variables). It gives more sensible interpretation of the behavior of the algorithm. Linear Programming 2010 14

1. 2 Formulation examples q Minimum cost network flow problem Directed network G=(N, A), (|N| = n ) arc capacity uij , (i, j) A, unit flow cost cij , (i, j) A bi : net supply at node i (bi > 0: supply node, bi < 0: demand node), ( i bi = 0) Find min cost transportation plan that satisfies supply, demand at each node and arc capacities. minimize subject to (i, j) A cijxij {j : (i, j) A} xij - {j : (j, i) A} xji = bi , i = 1, …, n (out flow - in flow = net flow at node i) (some people use, in flow – out flow = net flow) xij uij , (i, j) A xij 0 , (i, j) A Linear Programming 2010 15

q Choosing paths in a communication network ( (fractional) multicommodity flow problem) q Multicommodity flow problem: Several commodities share the network. For each commodity, it is min cost network flow problem. But the commodities must share the capacities of the arcs. Generalization of min cost network flow problem. Many applications in communication, distribution / transportation systems Ø Several commodities case Ø Actually one commodity. But there are multiple origin and destination pairs of nodes (telecom, logistics, . . ) q Given telecommunication network (directed) with arc set A, arc capacity uij bits/sec, (i, j) A, unit flow cost cij /bit , (i, j) A, demand bkl bits/sec for traffic from node k to node l. Data can be sent using more than one path. Find paths to direct demands with min cost. Linear Programming 2010 16

Decision variables: xijkl : amount of data with origin k and destination l that traverses link (i, j) A Let bikl = bkl if i = k -bkl if i = l 0 otherwise q Formulation (flow formulation) minimize subject to (i, j) A k l cijxijkl {j : (i, j) A} xijkl - {j : (j, i) A} xjikl = bikl , i, k, l = 1, …, n (out flow - in flow = net flow at node i for commodity from node k to node l) k l xijkl uij , (i, j) A (The sum of all commodities should not exceed the capacity of link (i, j) ) xijkl 0 , (i, j) A, k, l =1, …, n Linear Programming 2010 17

q Alternative formulation (path formulation) Let K: set of origin-destination pairs (commodities) P(k): set of all possible paths for sending commodity k K P(k; e): set of paths in P(k) that traverses arc e A E(p): set of links contained in path p Decision variables: ypk : fraction of commodity k sent on path p k K p P(k) wpkypk p P(k) ypk = 1, for all k K p P(k; e) bkypk ue , for all e A 0 ypk 1, for all p P(k), k K where wpk = bk e E(p) ce minimize subject to q If ypk {0, 1}, it is a single path routing problem (path selection, integer multicommodity flow). Linear Programming 2010 18

q path formulation has smaller number of constraints, but enormous number of variables. can be solved easily by column generation technique (later). Integer version is more difficult to solve. q Extensions: Network design - also determine the number and type of facilities to be installed on the links (and/or nodes) together with routing of traffic. q Variations: Integer flow. Bifurcation of traffic may not be allowed. Determine capacities and routing considering rerouting of traffic in case of network failure, Robust network design (data uncertainty), . . . Linear Programming 2010 19

q Pattern classification (Linear classifier) Given m objects with feature vector ai Rn , i = 1, …, m. Objects belong to one of two classes. We know the class to which each sample object belongs. We want to design a criterion to determine the class of a new object using the feature vector. Want to find a vector (x, xn+1) Rn+1 with x Rn such that, if i S, then ai'x xn+1, and if i S, then ai'x < xn+1. (if it is possible) Linear Programming 2010 20

q Find a feasible solution (x, xn+1) that satisfies ai'x xn+1, i S ai'x < xn+1. i S for all sample objects i Is this a linear programming problem? ( no objective function, strict inequality in constraints) Linear Programming 2010 21

q Is strict inequality allowed in LP? consider min x, x > 0 no minimum point. only infimum of objective value exists q If the system has a feasible solution (x, xn+1), we can make the difference of the rhs and lhs large by using solution M(x, xn+1) for M > 0 and large. Hence there exists a solution that makes the difference at least 1 if the system has a solution. Remedy: Use ai'x xn+1, i S ai'x xn+1 -1, i S q Important problem in data mining with applications in target marketing, bankruptcy prediction, medical diagnosis, process monitoring, … Linear Programming 2010 22

q Variations Ø What if there are many choices of hyperplanes? any reasonable criteria? Ø What if there is no hyperplane separating the two classes? Ø Do we have to use only one hyperplane? Ø Use of nonlinear function possible? How to solve them? • SVM (support vector machine), convex optimization Ø More than two classes? Linear Programming 2010 23

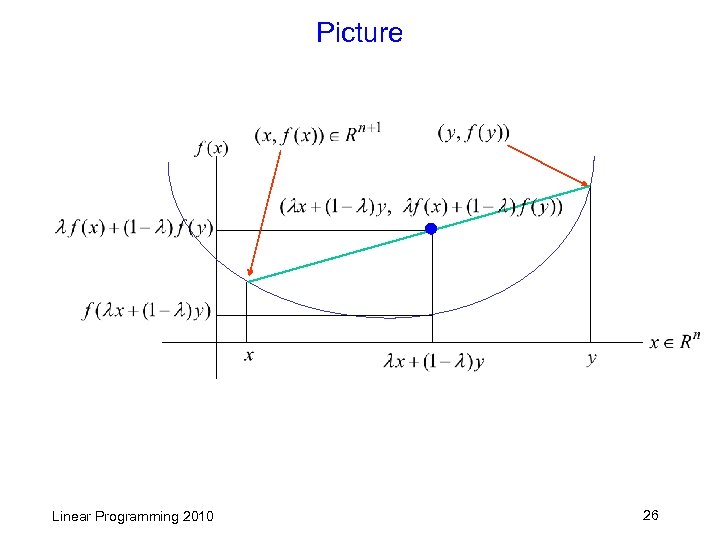
1. 3 Piecewise linear convex obj. functions q Some problems involving nonlinear functions can be modeled as LP. q Def: Function f : Rn R is called a convex function if for all x, y Rn and all [0, 1] f( x + (1 - )y) f(x) + (1 - )f(y). ( the domain may be restricted) f called concave if -f is convex (picture: the line segment joining (x, f(x)) and (y, f(y)) in Rn+1 is not below the locus of f(x) ) Linear Programming 2010 24

q Def: x, y Rn, 1, 2 0, 1+ 2 = 1 Then 1 x + 2 y is said to be a convex combination of x, y. Generally, i=1 k ixi , where i=1 k i = 1 and i 0, i = 1, . . . , k is a convex combination of the points x 1, . . . , xk q Def: A set S Rn is convex if for any x, y S, we have x + (1 - ) y S for any [ 0, 1 ]. Picture: 1 x + 2 y = 1 x + (1 - 1) y, 0 1 1 = y + 1 (x – y) (line segment joining x, y lies in S) x ( 1 = 1) (x-y) Linear Programming 2010 y ( 1 = 0) 25
Picture Linear Programming 2010 26

q relation between convex function and convex set q Def: f: Rn R. Define epigraph of f as epi(f) = { (x, ) Rn+1 : f(x) } q Then previous definition of convex function is equivalent to epi(f) being a convex set. When dealing with convex functions, we frequently consider epi(f) to exploit the properties of convex sets. q Consider operations on functions that preserve convexity and operations on sets that preserve convexity. Linear Programming 2010 27

q Example: Consider f(x) = max i = 1, …, m (ci'x + di), ci Rn, di R (maximum of affine functions, called a piecewise linear convex function. ) c 1'x+d 1 c 2'x+d 2 c 3'x+d 3 x Linear Programming 2010 28

q Thm: Let f 1, …, fm : Rn R be convex functions. Then f(x) = max i = 1, …, m fi(x) is also convex. pf) f( x + (1 - )y) = max i=1, …, m fi( x + (1 - )y ) max i=1, …, m ( fi(x) + (1 - )fi(y) ) max i=1, …, m fi(x) + max i=1, …, m (1 - )fi(y) = f(x) + (1 - )f(y) Linear Programming 2010 29

q Min of piecewise linear convex functions Minimize max I=1, …, m (ci'x + di) Subject to Ax b Minimize Subject to Linear Programming 2010 z z ci'x + di , Ax b i = 1, …, m 30

q Q: What can we do about finding max of a piecewise linear convex function? maximum of a piecewise linear concave function (can be obtained as min of affine functions)? Min of a piecewise linear concave function? Linear Programming 2010 31

q Convex function has a nice property such that a local min point is a global min point. (when domain is Rn or convex set) (HW later) Hence finding min of a convex function defined over a convex set is usually easy. But finding a max of a convex function is difficult to solve. Basically, we need to examine all local max points. Similarly, finding a max of concave function is easy, but finding min of a concave function is difficult. Linear Programming 2010 32

q In constraints, f(x) h where f(x) is piecewise linear convex function f(x) = max i=1, …, m (fi'x + gi). fi'x + gi h, i = 1, … , m Q: What about constraints f(x) h ? Can it be modeled as LP? q Def: f: Rn R, convex function, R The set C = { x: f(x) } is called the level set of f q level set of a convex function is a convex set. (HW later) solution set of LP is convex (easy) non-convex solution set can’t be modeled as LP. Linear Programming 2010 33

Problems involving absolute values q Minimize i = 1, …, n ci |xi| subject to Ax b (assume ci 0) More direct formulations than piecewise linear convex function is possible. (1) Min i ci zi subject to Ax b xi zi , i = 1, …, n -xi zi , i = 1, …, n Linear Programming 2010 (2) Min i ci (xi+ + xi-) subject to Ax+ - Ax- b x + , x- 0 (want xi+ = xi if xi 0, xi- = -xi if xi < 0 and xi+xi- = 0, i. e. , at most one of xi+, xi- is positive in an optimal solution. ci 0 guarantees that. ) 34

Data Fitting q Regression analysis using absolute value function Given m data points (ai , bi ), i = 1, …, m, ai Rn , bi R. Want to find x Rn that predicts results b given a with function b = a'x Want x that minimizes prediction error | bi - ai'x | for all i. minimize subject to z bi - ai'x z, i = 1, … , m -bi + ai'x z, i = 1, … , m Linear Programming 2010 35

q Alternative criterion minimize i = 1, …, m | bi - ai'x | minimize subject to z 1 + … + zm bi - ai'x zi , i = 1, … , m -bi + ai'x zi , i = 1, … , m Quadratic error function can't be modeled as LP, but need calculus method (closed form solution) Linear Programming 2010 36
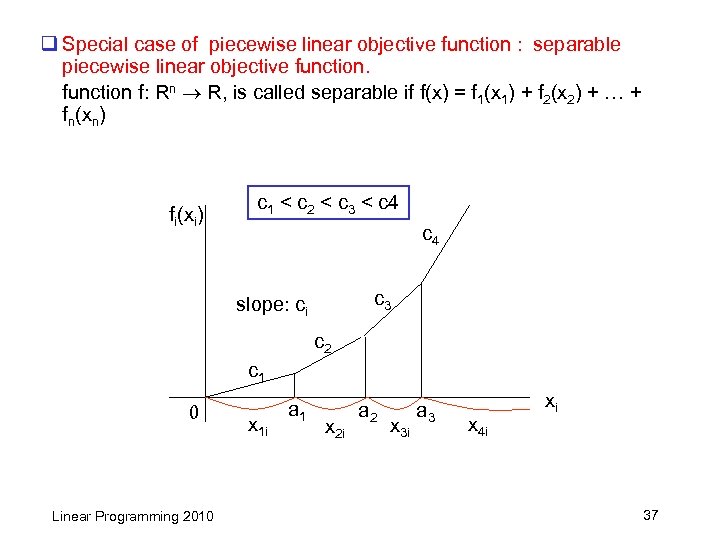
q Special case of piecewise linear objective function : separable piecewise linear objective function f: Rn R, is called separable if f(x) = f 1(x 1) + f 2(x 2) + … + fn(xn) fi(xi) c 1 < c 2 < c 3 < c 4 c 3 slope: ci c 2 c 1 0 Linear Programming 2010 x 1 i a 1 x 2 i a 2 x 3 i a 3 x 4 i xi 37

q Express xi in the constraints as xi x 1 i + x 2 i + x 3 i + x 4 i , where 0 x 1 i a 1, 0 x 2 i a 2 - a 1 , 0 x 3 i a 3 - a 2, 0 x 4 i In the objective function, use : min c 1 x 1 i + c 2 x 2 i + c 3 x 3 i + c 4 x 4 i Since we solve min problem, it is guaranteed that we get xki > 0 in an optimal solution implies xji , j < k have values at their upper bounds. Linear Programming 2010 38

1. 4 Graphical representation and solution q Let a Rn, b R. Geometric intuition for the solution sets of { x : a’x = 0 } { x : a’x = b } { x : a’x b } Linear Programming 2010 39
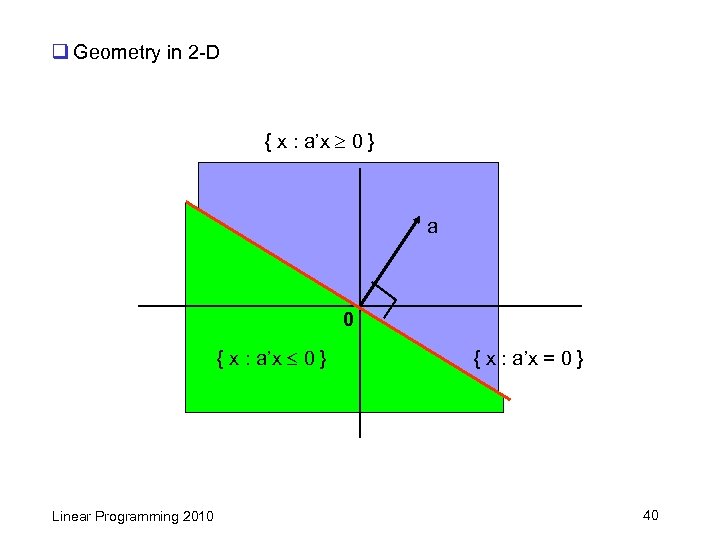
q Geometry in 2 -D { x : a’x 0 } a 0 { x : a’x 0 } Linear Programming 2010 { x : a’x = 0 } 40
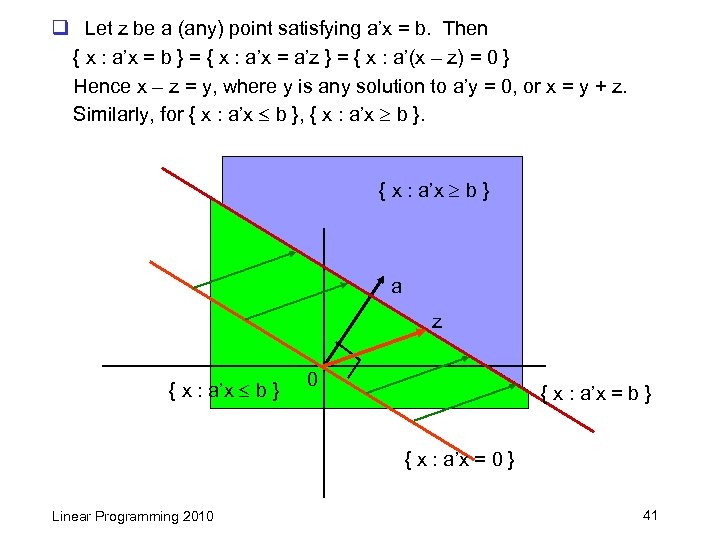
q Let z be a (any) point satisfying a’x = b. Then { x : a’x = b } = { x : a’x = a’z } = { x : a’(x – z) = 0 } Hence x – z = y, where y is any solution to a’y = 0, or x = y + z. Similarly, for { x : a’x b }, { x : a’x b } a z { x : a’x b } 0 { x : a’x = b } { x : a’x = 0 } Linear Programming 2010 41
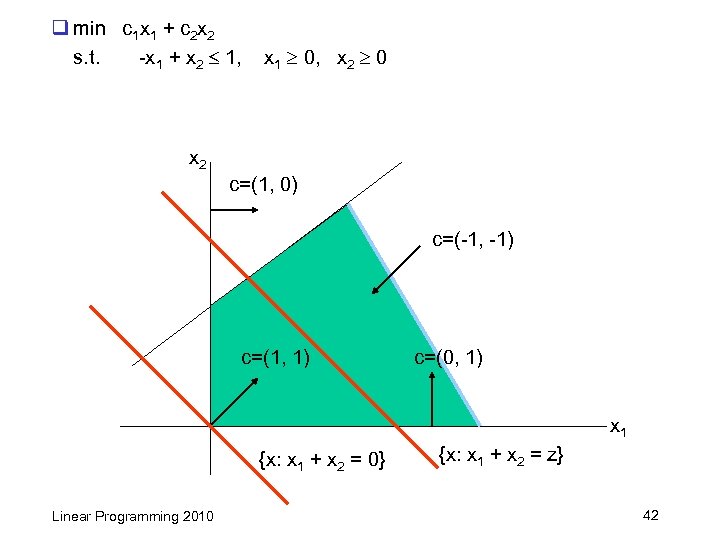
q min c 1 x 1 + c 2 x 2 s. t. -x 1 + x 2 1, x 1 0, x 2 0 x 2 c=(1, 0) c=(-1, -1) c=(1, 1) c=(0, 1) x 1 {x: x 1 + x 2 = 0} Linear Programming 2010 {x: x 1 + x 2 = z} 42
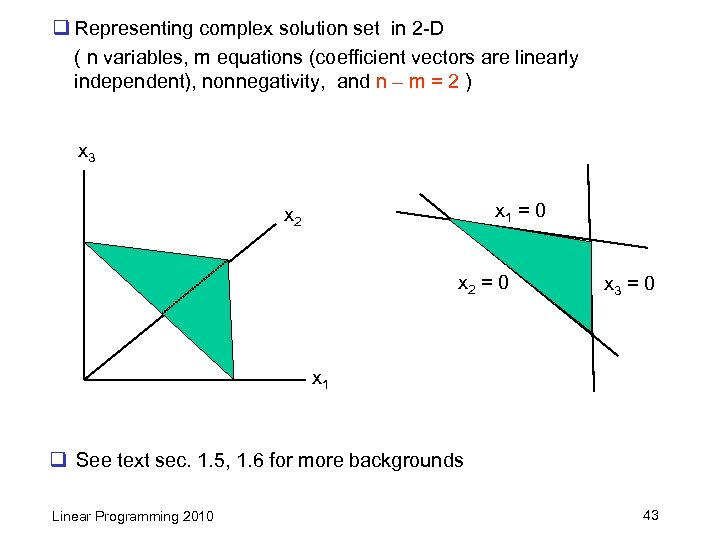
q Representing complex solution set in 2 -D ( n variables, m equations (coefficient vectors are linearly independent), nonnegativity, and n – m = 2 ) x 3 x 1 = 0 x 2 = 0 x 3 = 0 x 1 q See text sec. 1. 5, 1. 6 for more backgrounds Linear Programming 2010 43
c8731abc47bcaddcf1cc1e11f3175ffb.ppt