b46294c427555da4fef6cdb908043ec4.ppt
- Количество слайдов: 30
 Identity & Inverse Matrices
Identity & Inverse Matrices
 Identity What does “identity” mean to you? What is the multiplicative identity for the real numbers? In other words, 5 * __= 5? The identity for multiplication is 1 because anything multiplied by 1 will be itself.
Identity What does “identity” mean to you? What is the multiplicative identity for the real numbers? In other words, 5 * __= 5? The identity for multiplication is 1 because anything multiplied by 1 will be itself.
 Inverses What does “inverse” mean to you? What is the inverse of multiplication?
Inverses What does “inverse” mean to you? What is the inverse of multiplication?
 What do we multiply by to get the identity? In other words, 5 * ___=1? a * -1= a 1 Any number multiplied by its inverse will be the identity.
What do we multiply by to get the identity? In other words, 5 * ___=1? a * -1= a 1 Any number multiplied by its inverse will be the identity.
 Identity Matrix The multiplicative identity for matrices is a square matrix with ones on the main diagonal and zeros everywhere else.
Identity Matrix The multiplicative identity for matrices is a square matrix with ones on the main diagonal and zeros everywhere else.
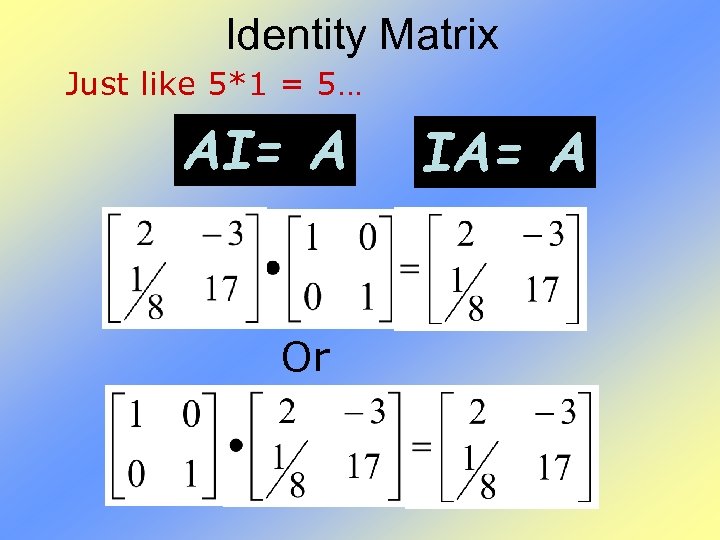 Identity Matrix Just like 5*1 = 5… AI= A Or IA= A
Identity Matrix Just like 5*1 = 5… AI= A Or IA= A
 Identity Matrix Any matrix multiplied by its inverse will be the identity matrix. A * -1 A -1= A I *A = I 2 x 2 Identity Matrix 3 x 3 Identity Matrix
Identity Matrix Any matrix multiplied by its inverse will be the identity matrix. A * -1 A -1= A I *A = I 2 x 2 Identity Matrix 3 x 3 Identity Matrix
 Ex. 1 Determine whether A and B are inverses. YES
Ex. 1 Determine whether A and B are inverses. YES
 Ex. 2 Determine whether A and B are inverses. NO
Ex. 2 Determine whether A and B are inverses. NO
 The Inverse of a 2 x 2 Matrix If ad-cd=0, then the matrix has no inverse!!!! -1= A As long as ad-cb =0
The Inverse of a 2 x 2 Matrix If ad-cd=0, then the matrix has no inverse!!!! -1= A As long as ad-cb =0
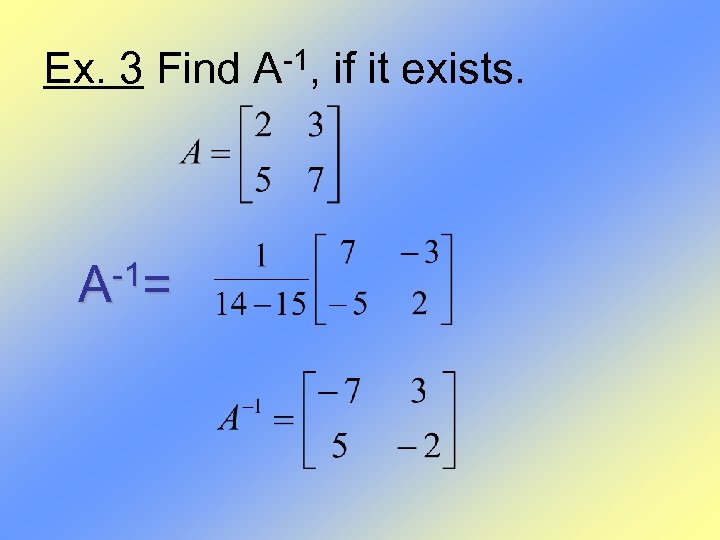 Ex. 3 Find A-1, if it exists. -1= A
Ex. 3 Find A-1, if it exists. -1= A
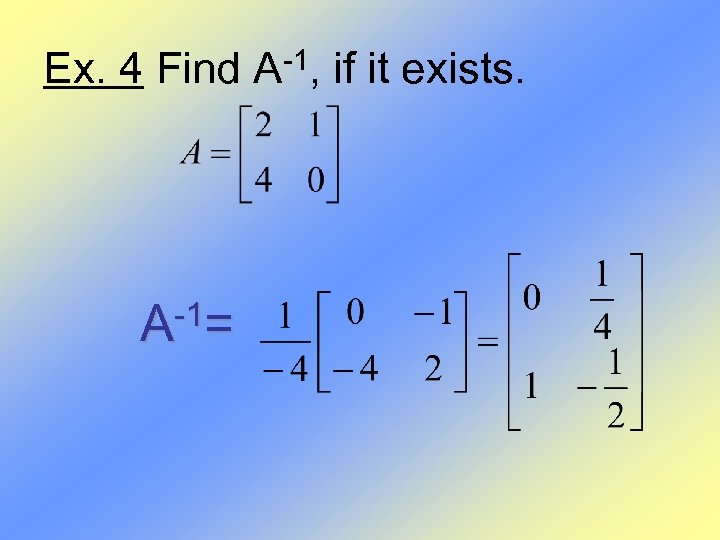 Ex. 4 Find A-1, if it exists. -1= A
Ex. 4 Find A-1, if it exists. -1= A
 Ex. 5 Find A-1, if it exists. Does not exist, because it’s not square.
Ex. 5 Find A-1, if it exists. Does not exist, because it’s not square.
 Now let’s learn how to use our calculator!!!
Now let’s learn how to use our calculator!!!
 Find the inverse! Yes, now you can add, subtract, multiply, and find the determinant in you calculator!!
Find the inverse! Yes, now you can add, subtract, multiply, and find the determinant in you calculator!!
 Solving Systems using Matrices and Inverses
Solving Systems using Matrices and Inverses
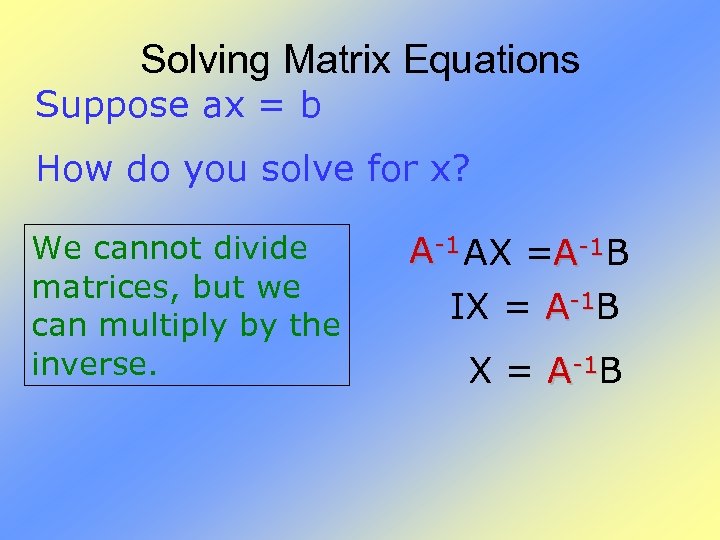 Solving Matrix Equations Suppose ax = b How do you solve for x? We cannot divide matrices, but we can multiply by the inverse. A-1 AX =A-1 B IX = A-1 B
Solving Matrix Equations Suppose ax = b How do you solve for x? We cannot divide matrices, but we can multiply by the inverse. A-1 AX =A-1 B IX = A-1 B
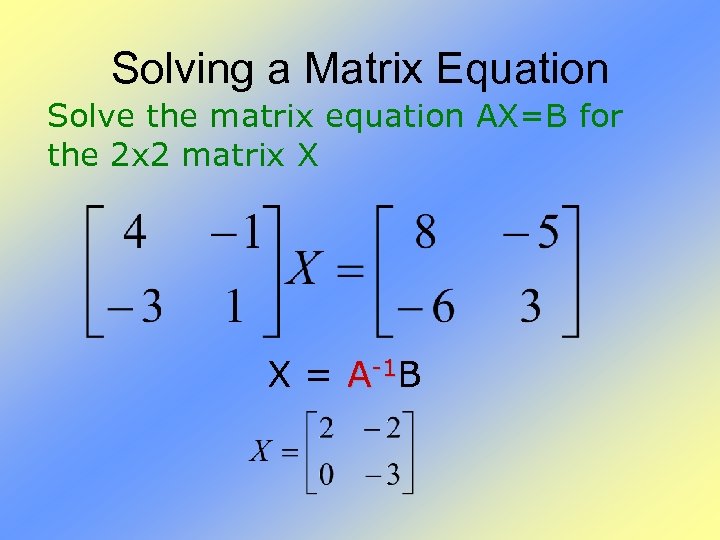 Solving a Matrix Equation Solve the matrix equation AX=B for the 2 x 2 matrix X X = A-1 B
Solving a Matrix Equation Solve the matrix equation AX=B for the 2 x 2 matrix X X = A-1 B
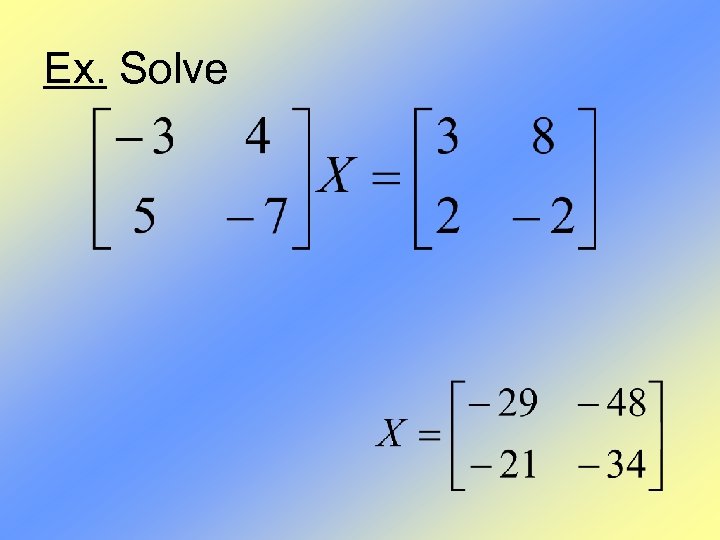 Ex. Solve
Ex. Solve
 Solving Systems Using Inverse Matrices
Solving Systems Using Inverse Matrices
 Setting Up the Matrices • Matrix A will be the coefficients of the system • Matrix X will be the variables • Matrix B will be constants (what the system of equations are equal to)
Setting Up the Matrices • Matrix A will be the coefficients of the system • Matrix X will be the variables • Matrix B will be constants (what the system of equations are equal to)
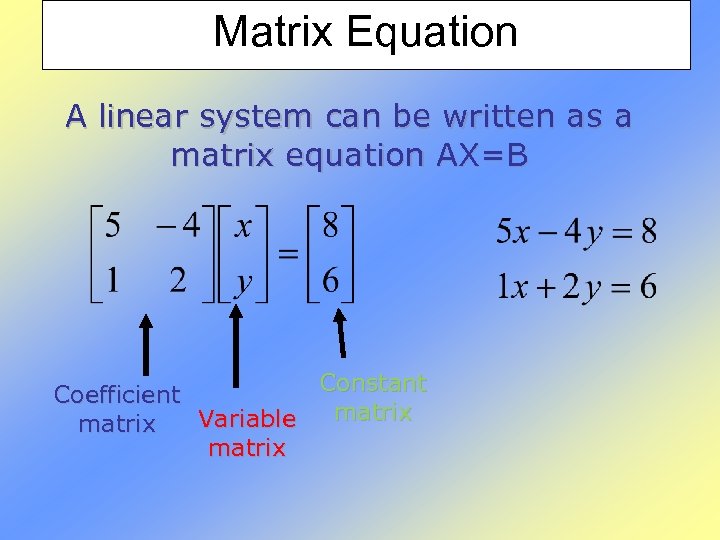 Matrix Equation A linear system can be written as a matrix equation AX=B Constant Coefficient matrix Variable matrix
Matrix Equation A linear system can be written as a matrix equation AX=B Constant Coefficient matrix Variable matrix
 Example 1
Example 1
![Example 2: Use matrices to solve the linear system Type in [A]-1 [B] Find Example 2: Use matrices to solve the linear system Type in [A]-1 [B] Find](https://present5.com/presentation/b46294c427555da4fef6cdb908043ec4/image-24.jpg) Example 2: Use matrices to solve the linear system Type in [A]-1 [B] Find the inverse (-1, 4)
Example 2: Use matrices to solve the linear system Type in [A]-1 [B] Find the inverse (-1, 4)
![Example 3: Use matrices to solve the linear system Type in [A]-1 [B] Find Example 3: Use matrices to solve the linear system Type in [A]-1 [B] Find](https://present5.com/presentation/b46294c427555da4fef6cdb908043ec4/image-25.jpg) Example 3: Use matrices to solve the linear system Type in [A]-1 [B] Find the inverse (4, 4)
Example 3: Use matrices to solve the linear system Type in [A]-1 [B] Find the inverse (4, 4)
![Example 4: Use matrices to solve the linear system Type in [A]-1 [B] (-2, Example 4: Use matrices to solve the linear system Type in [A]-1 [B] (-2,](https://present5.com/presentation/b46294c427555da4fef6cdb908043ec4/image-26.jpg) Example 4: Use matrices to solve the linear system Type in [A]-1 [B] (-2, 3, 1)
Example 4: Use matrices to solve the linear system Type in [A]-1 [B] (-2, 3, 1)
![Example 5: Use matrices to solve the linear system Type in [A]-1 [B] (2, Example 5: Use matrices to solve the linear system Type in [A]-1 [B] (2,](https://present5.com/presentation/b46294c427555da4fef6cdb908043ec4/image-27.jpg) Example 5: Use matrices to solve the linear system Type in [A]-1 [B] (2, 3, -2)
Example 5: Use matrices to solve the linear system Type in [A]-1 [B] (2, 3, -2)
 Let’s apply this… You have $18 to spend for lunch during a 5 day school week. It costs you $1. 50 to make lunch at home and $5 to buy lunch. How many times each week do you make a lunch at home? (2, 3) Type in [A]-1 [B] You make lunch at home 2 times a week.
Let’s apply this… You have $18 to spend for lunch during a 5 day school week. It costs you $1. 50 to make lunch at home and $5 to buy lunch. How many times each week do you make a lunch at home? (2, 3) Type in [A]-1 [B] You make lunch at home 2 times a week.
 A word problem…!! • A small corporation borrowed $1, 500, 000 to expand its product line. Some of the money was borrowed at 8%, some at 9% and some at 12%. How much was borrowed at each rate if the annual interest was $133, 000 and the amount borrowed at 8% was 4 times the amount borrowed at 12%? $800, 000 at 8% $500, 000 at 9% $200, 000 at 12%
A word problem…!! • A small corporation borrowed $1, 500, 000 to expand its product line. Some of the money was borrowed at 8%, some at 9% and some at 12%. How much was borrowed at each rate if the annual interest was $133, 000 and the amount borrowed at 8% was 4 times the amount borrowed at 12%? $800, 000 at 8% $500, 000 at 9% $200, 000 at 12%
 Homework
Homework


