ИДЕНТИФИКАЦИЯ СТАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ
Общие понятия Идентификация – это процесс построения моделей объектов различной природы. Теория идентификации имеет в своем арсенале достаточно эффективные методы и алгоритмы, на базе которых разработаны и широко используются программные комплексы. Процесс идентификации складывается из двух взаимосвязанных этапов: идентификации структуры моделей и идентификации параметров в моделях выбранной структуры. При построении структуры модели (или набора конкурирующих либо взаимодополняющих структур) используется априорная информация об объекте. Для каждого класса объектов формируются банки структур с сопутствующей информацией. Модели делятся на статические и динамические. Первые из них описывают объекты в стационарных режимах их работы. Динамические модели описывают переходные процессы в объектах, например, возникающие при переходе с одного стационарного режима работы объекта на другой.
Постановка задачи подстройки параметров нелинейных моделей Считаем, что выход объекта состоит из полезного сигнала η(u, a) и центрированной помехи ξ. Сигнальная часть выхода представляет собой известную функцию от входа с неизвестными параметрами a. В структуру функции η(u, a). Все, что не удается описать в объекте, относят к помехе. Модель объекта берем в виде функции η(u, α). Основная задача теперь сводится к расчету параметров α модели. Алгоритмы расчета будем строить, используя критерий наименьших квадратов и близкие к нему критерии, например наименьших модулей невязок. В зависимости от свойств помехи критерий наименьших квадратов приобретает различные формы – от простейшей до самой общей.
Критерий наименьших квадратов Считаем, что в каждый момент времени ti (момент измерения входа и выхода объекта) помехи ξi, являются центрированными случайными величинами с дисперсиями σi 2. Если дисперсии различны, то измерения называются неравноточными. Тогда критерий наименьших квадратов имеет вид: При равноточных измерениях весовые коэффициенты 1/σi 2, характеризующие информативность измерений, одинаковы. Тогда критерий имеет вид:
Критерий наименьших квадратов Если все помехи ξi коррелированны, т. е: то критерий наименьших квадратов базируется на элементах cij матрицы, обратной корреляционной: Это общая форма критерия. Она включает в себя (при соответствующих упрощениях) все предыдущие формы. Запишем критерий в матричной форме.
Метод наименьших квадратов при линейной параметризации модели Модель объекта задана в виде линейной комбинации известных (базисных) функций φ1(u), …, φm(u): Параметры α находим по критерию наименьших квадратов:
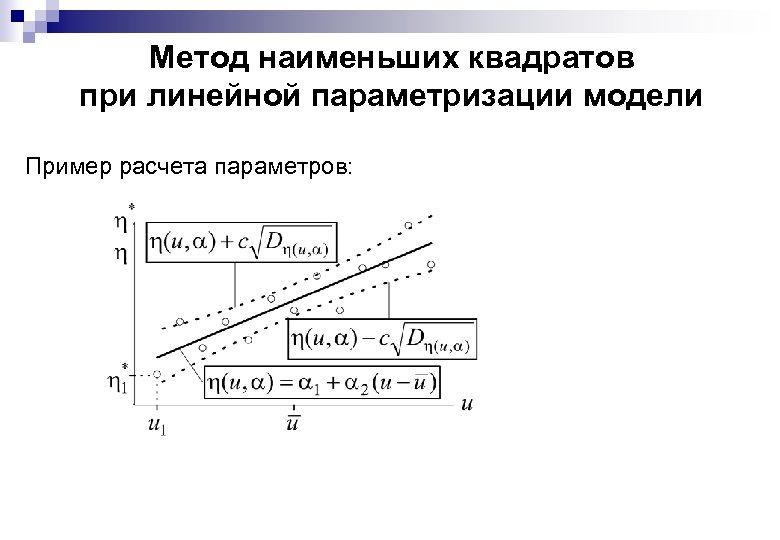
Метод наименьших квадратов при линейной параметризации модели Пример расчета параметров:
Метод последовательной линеаризации при подстройке параметров на основе критерия наименьших квадратов Построим итерационную процедуру расчета параметров α модели в соответствии с критерием наименьших квадратов. Так как функционал квадратичный, то первая стадия метода не реализуется и на каждой итерации используется только линейная аппроксимация выхода модели по параметрам: Необходимое условие минимума приводит к системе линейных алгебраических уравнений:
Робастные оценки параметров Параметры модели (которые являются оценками параметров объекта), полученные на основе критерия наименьших квадратов, сильно реагируют на выбросы помех. Аномальные отклонения в измерениях очень редки, но амплитуда их велика. Так же существуют другие критерии вида: Примеры функции ψ(e):
Простейший адаптивный алгоритм подстройки параметров Линейная параметризация модели: На каждой итерации, например n и n-1, параметры модели находим из условия равенства выходов модели и объекта: Каждому уравнению в пространстве параметров соответствует своя линия
Простейший адаптивный алгоритм подстройки параметров Нелинейная модель: На каждом шаге линеаризуем модель и приращения параметров отыскиваем из равенства (эквивалентного (6. 8. 2) для линейного случая) выхода модели и линеаризованной модели В итоге получаем алгоритм перестройки параметров нелинейной модели:
Скачать презентацию ИДЕНТИФИКАЦИЯ СТАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ Общие понятия Идентификация
78c8eed240e7ddee0d176d891672be20.ppt