Ideal Gas Law for Moist Air The

Ideal Gas Law for Moist Air · The value for the meteorological R on the last page was derived assuming dry air. · The concentration of water vapor is a highly variable quantity in the lower atmosphere. · R could be modified to account of this variability. · R becomes Rd(1 + 0. 61 r), where r is the mixing ratio (the mass of water vapor divided by the mass of dry air). · The meteorological ideal gas law becomes P = Rd (1 + 0. 61 r) T · However, in practice, most meteorologists prefer to write this as P = Rd Tv, where Tv is the virtual temperature Tv = T(1 + 0. 61 r) · CAUTION: T and Tv are in units of K, not C bourassa@met. fsu. edu The Florida State University

Derivation of Virtual Temperature · A Partial Pressure is the pressure due to one type of gas molecule. The partial pressures sum to the total pressure. · The partial pressure for dry air is · Pd = d Rd T, Rd = 287 J K-1 kg-1 · d is the density of dry air. · The partial pressure for water vapor is · Pv = v Rv T, Rv = 461. 5 J K-1 kg-1 · v is the density of water vapor. · In meteorological applications it is common to use the symbol e to · indicate the partial pressure of water vapor. · e = v Rv T The total pressure is P = Pd + e bourassa@met. fsu. edu The Florida State University

Derivation of Virtual Temperature · The density of moist air can be written as · = (md + me) / V = d + v · Where d and v are determined assuming that only the dry air occupied the whole volume V, and that only the water vapor occupied the whole volume V. · Then · = (P - e) / (Rd T) + e / (Rv T) · Where = Rd / Rv = Mw / Md = 0. 6219 · Then bourassa@met. fsu. edu The Florida State University

Derivation of Virtual Temperature · The ideal gas law can be used to show that e / P is equal to · Where r is the mixing ratio, the mass of water vapor divided by the mass of dry air, usually discussed in units of g water vapor per kg of dry air, but applied in kg water vapor / kg dry air. · Consider that 1/(1 -x) can be approximated as 1+x, provided that x is small. Therefore Tv T ( 1 + 0. 61 r ) bourassa@met. fsu. edu The Florida State University

More on Virtual Temperature · Virtual temperature is a fictitious temperature rather than an actual · · · temperature. Virtual temperature is the temperature that dry air would have to achieve to have the same density as moist air at the same pressure as the dry air. Since moist air is less dense than dry air, the virtual temperature is always equal to or greater than the actual temperature. Even for very moist air, the virtual temperature is only a few degrees warmer than the actual temperature. bourassa@met. fsu. edu The Florida State University

Application of the Hydrostatic Equation · One of the key equations in Meteorology is the hydrostatic equation. · It describes the change in pressure with changes in height. P/ z = - g · Integrate the hydrostatic equation from the height of interest to the top of the atmosphere (approximated as infinity). · This result indicates that the pressure at any height in the atmosphere is equal to the weight of the air above that height, within a column of unit area (that is, a column that has an area of 1 in the units of distance squared). bourassa@met. fsu. edu The Florida State University

How Rapidly Does Pressure Change With Increasing Height? · Consider both the Hydrostatic Equation and the ideal gas law. P/ z = - g P = R d Tv · Solve the ideal gas law for density, and replace density in the · hydrostatic equation P/ z = -(P / Rd Tv) g Solving this results in an approximately logarithmic change in pressure with changes in altitude (assuming Rd and Tv are constant): · ln(P) / z = -g / Rd Tv, or ln(P) = -(g / Rd Tv) z z 2 – z 1 = (Rd / g) Tv ln(P 1 / P 2 ) (Hypsometric Equation) ln(P(z)) = ln(Psfc) -(g / (Rd Tv) ) z P(z) = Psfc exp(-g z / (Rd Tv) ) · Approximate because Tv is not constant. · The rate of change of pressure with height decreases as the pressure decreases (i. e. , as the height increases). bourassa@met. fsu. edu The Florida State University

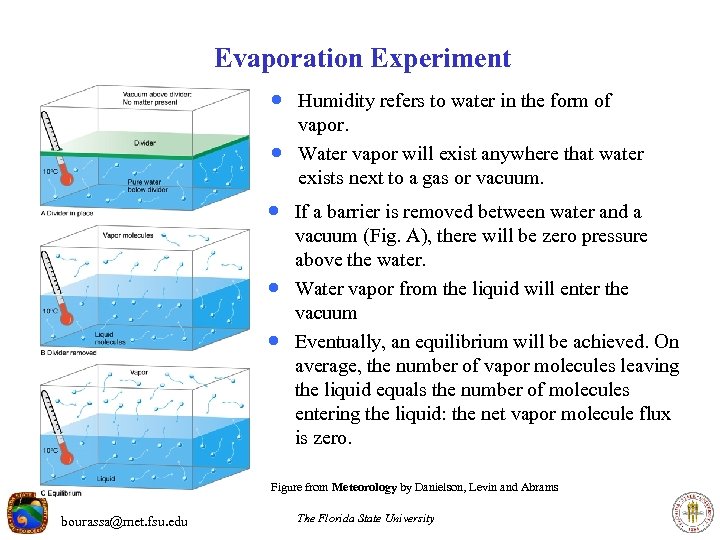Evaporation Experiment · Humidity refers to water in the form of · vapor. Water vapor will exist anywhere that water exists next to a gas or vacuum. · If a barrier is removed between water and a · · vacuum (Fig. A), there will be zero pressure above the water. Water vapor from the liquid will enter the vacuum Eventually, an equilibrium will be achieved. On average, the number of vapor molecules leaving the liquid equals the number of molecules entering the liquid: the net vapor molecule flux is zero. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Partial Pressures · The equilibrium water vapor pressure in the previous example, would not change if there were additional gases in the system, so long as the temperature did not change. · Each of these pressures (called partial pressures) can be determined from the · · ideal gas law (Chemistry version, or Meteorology version): P = (n / v) R T or P = (R/Md) T The sum of the partial pressures is the total pressure. The vapor pressure is the partial pressure of water vapor. bourassa@met. fsu. edu The Florida State University

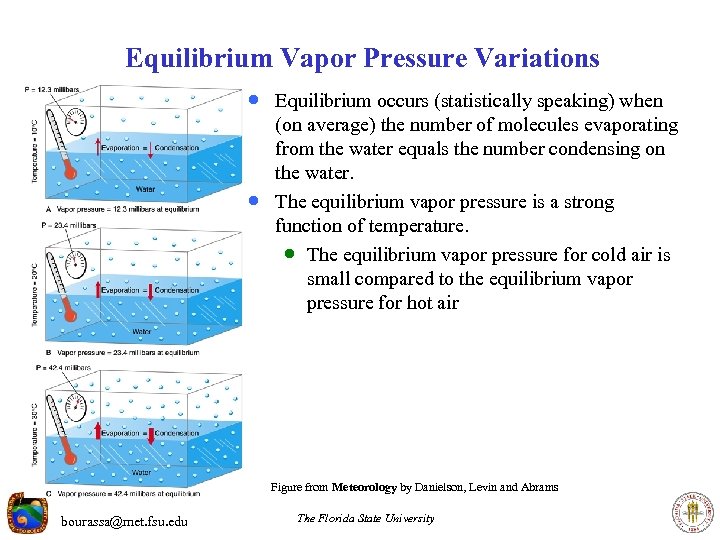Equilibrium Vapor Pressure Variations · Equilibrium occurs (statistically speaking) when · (on average) the number of molecules evaporating from the water equals the number condensing on the water. The equilibrium vapor pressure is a strong function of temperature. · The equilibrium vapor pressure for cold air is small compared to the equilibrium vapor pressure for hot air Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

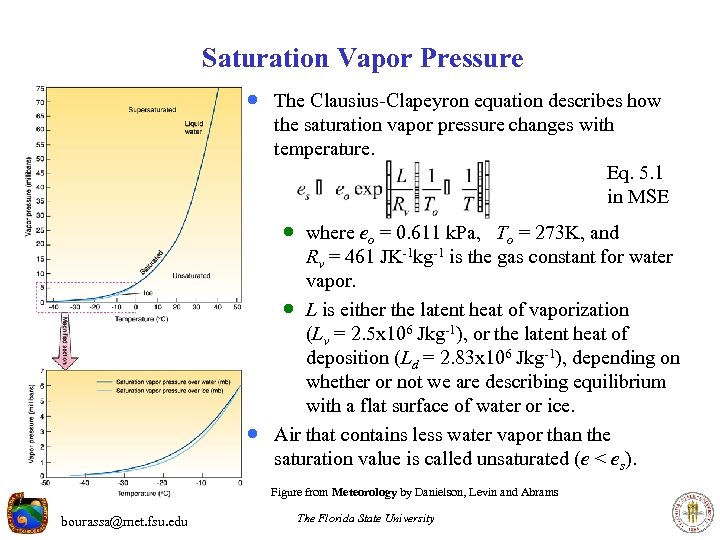Saturation Vapor Pressure · The Clausius-Clapeyron equation describes how the saturation vapor pressure changes with temperature. Eq. 5. 1 in MSE · where eo = 0. 611 k. Pa, To = 273 K, and · Rv = 461 JK-1 kg-1 is the gas constant for water vapor. · L is either the latent heat of vaporization (Lv = 2. 5 x 106 Jkg-1), or the latent heat of deposition (Ld = 2. 83 x 106 Jkg-1), depending on whether or not we are describing equilibrium with a flat surface of water or ice. Air that contains less water vapor than the saturation value is called unsaturated (e < es). Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

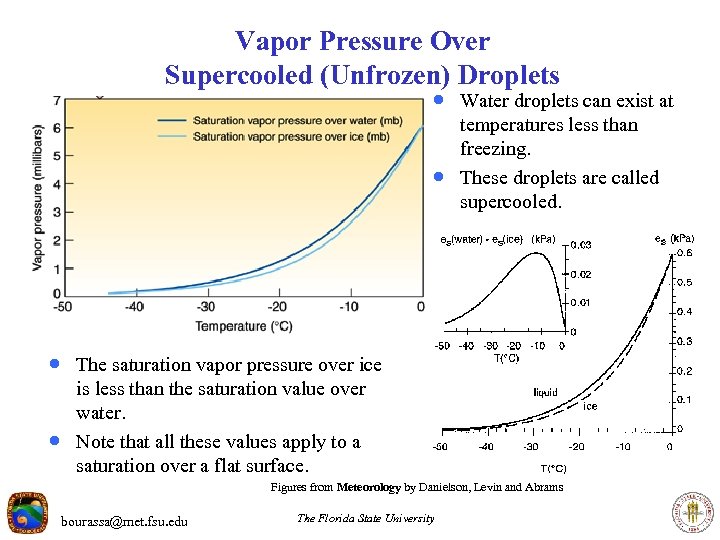Vapor Pressure Over Supercooled (Unfrozen) Droplets · Water droplets can exist at · temperatures less than freezing. These droplets are called supercooled. · The saturation vapor pressure over ice · is less than the saturation value over water. Note that all these values apply to a saturation over a flat surface. Figures from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

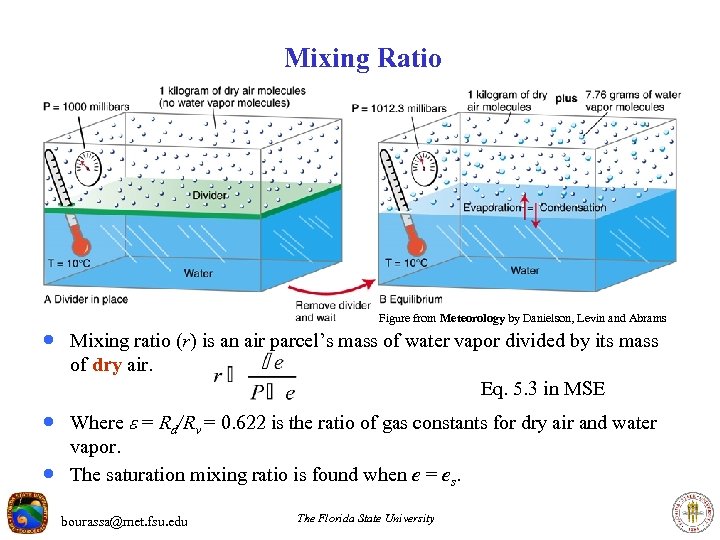Mixing Ratio Figure from Meteorology by Danielson, Levin and Abrams · Mixing ratio (r) is an air parcel’s mass of water vapor divided by its mass of dry air. Eq. 5. 3 in MSE · Where = Rd/Rv = 0. 622 is the ratio of gas constants for dry air and water · vapor. The saturation mixing ratio is found when e = es. bourassa@met. fsu. edu The Florida State University

Specific Humidity vs. Mixing Ratio · The specific humidity (q) is the air parcel’s mass of water vapor divided by it’s total mass (dry air plus water vapor). (Page 99 of MSE). · The absolute humidity ( v) is the concentration of water vapor in air, times the molecular mass (with mass in kg). · It has the same units as density. bourassa@met. fsu. edu The Florida State University

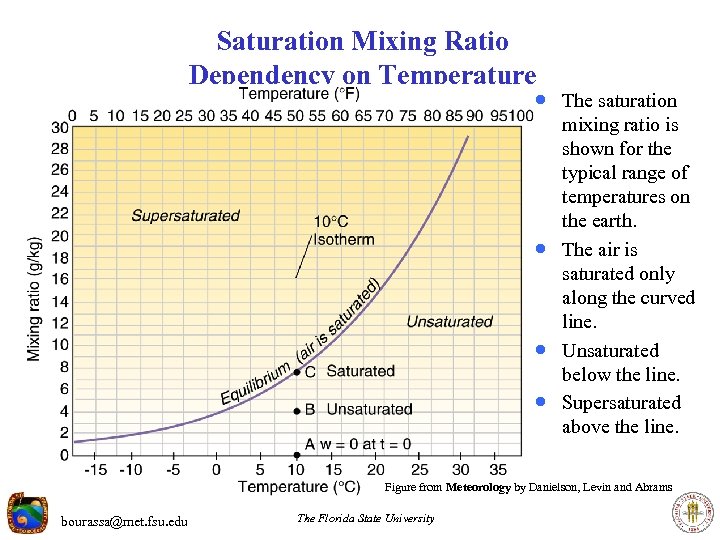Saturation Mixing Ratio Dependency on Temperature · The saturation · · · mixing ratio is shown for the typical range of temperatures on the earth. The air is saturated only along the curved line. Unsaturated below the line. Supersaturated above the line. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

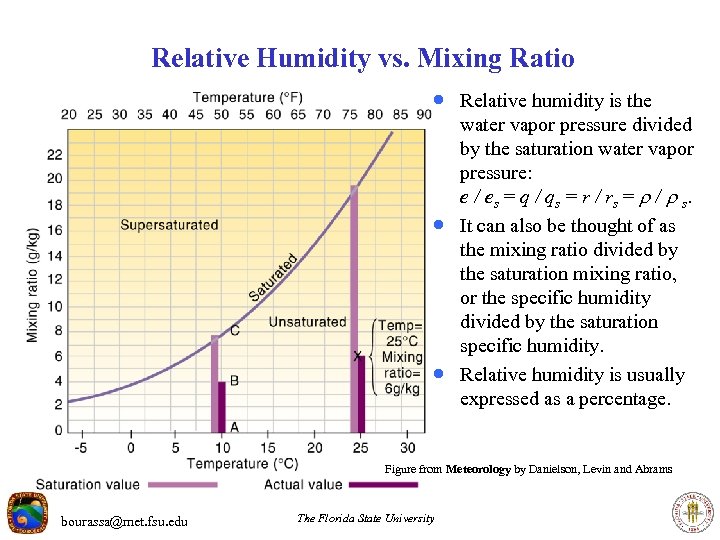Relative Humidity vs. Mixing Ratio · Relative humidity is the · · water vapor pressure divided by the saturation water vapor pressure: e / es = q / qs = r / rs = / s. It can also be thought of as the mixing ratio divided by the saturation mixing ratio, or the specific humidity divided by the saturation specific humidity. Relative humidity is usually expressed as a percentage. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

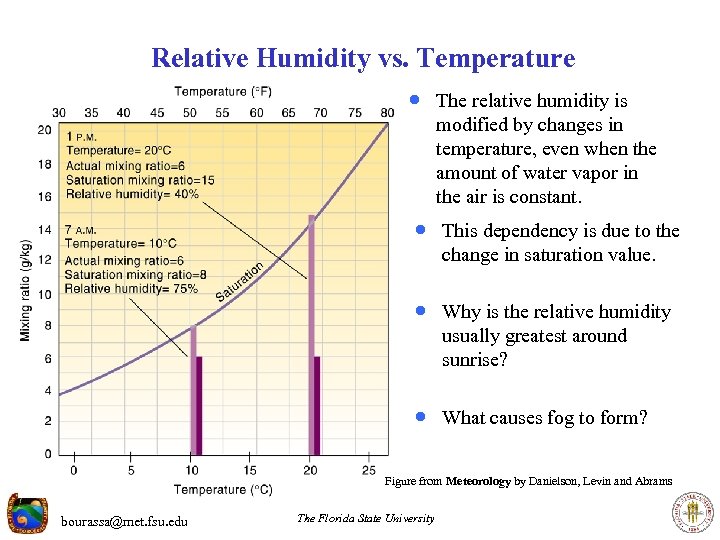Relative Humidity vs. Temperature · The relative humidity is modified by changes in temperature, even when the amount of water vapor in the air is constant. · This dependency is due to the change in saturation value. · Why is the relative humidity usually greatest around sunrise? · What causes fog to form? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

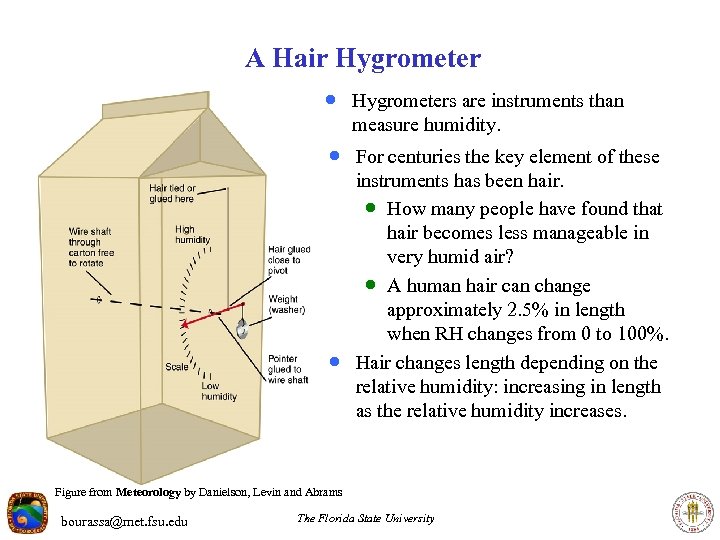A Hair Hygrometer · Hygrometers are instruments than measure humidity. · For centuries the key element of these · instruments has been hair. · How many people have found that hair becomes less manageable in very humid air? · A human hair can change approximately 2. 5% in length when RH changes from 0 to 100%. Hair changes length depending on the relative humidity: increasing in length as the relative humidity increases. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

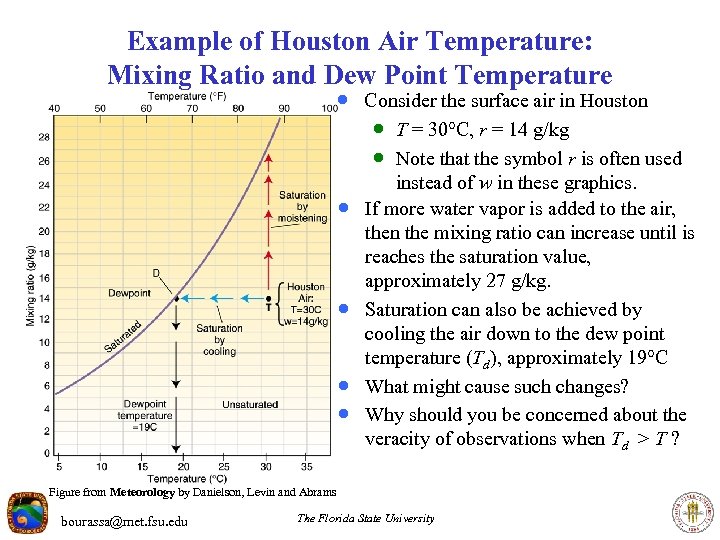Example of Houston Air Temperature: Mixing Ratio and Dew Point Temperature · Consider the surface air in Houston · T = 30 C, r = 14 g/kg · Note that the symbol r is often used · · instead of w in these graphics. If more water vapor is added to the air, then the mixing ratio can increase until is reaches the saturation value, approximately 27 g/kg. Saturation can also be achieved by cooling the air down to the dew point temperature (Td), approximately 19 C What might cause such changes? Why should you be concerned about the veracity of observations when Td > T ? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

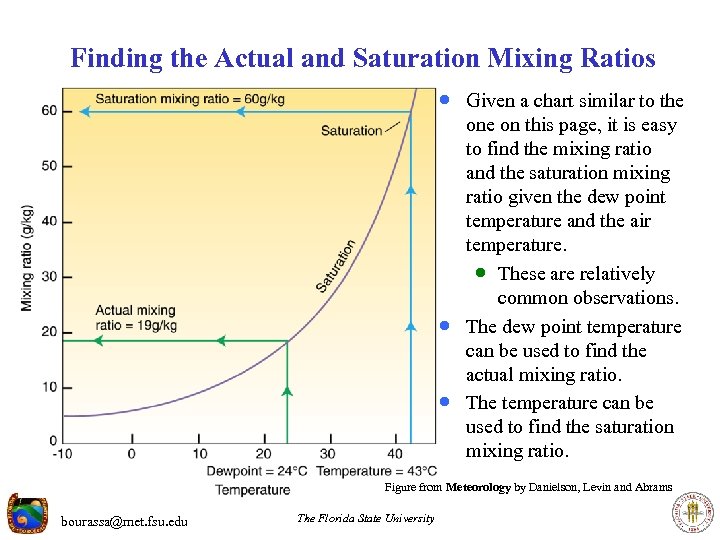Finding the Actual and Saturation Mixing Ratios · Given a chart similar to the · · one on this page, it is easy to find the mixing ratio and the saturation mixing ratio given the dew point temperature and the air temperature. · These are relatively common observations. The dew point temperature can be used to find the actual mixing ratio. The temperature can be used to find the saturation mixing ratio. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Calculating the Dew Point Temperature · The dew point temperature can be modeled, and then determined without the use of charts (page 100 in MSE). · Start from the Clausius-Clapeyron equation · Replace T with Td and es with e, where e is the observed vapor pressure, and Td is the temperature for which that amount of vapor would saturate the air. · Solving for Td bourassa@met. fsu. edu The Florida State University

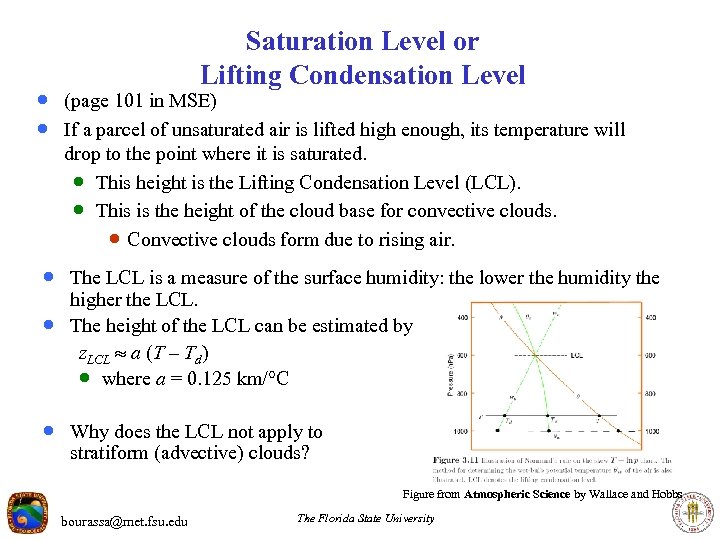Saturation Level or Lifting Condensation Level · (page 101 in MSE) · If a parcel of unsaturated air is lifted high enough, its temperature will drop to the point where it is saturated. · This height is the Lifting Condensation Level (LCL). · This is the height of the cloud base for convective clouds. · Convective clouds form due to rising air. · The LCL is a measure of the surface humidity: the lower the humidity the · higher the LCL. The height of the LCL can be estimated by z. LCL a (T – Td) · where a = 0. 125 km/ C · Why does the LCL not apply to stratiform (advective) clouds? Figure from Atmospheric Science by Wallace and Hobbs bourassa@met. fsu. edu The Florida State University

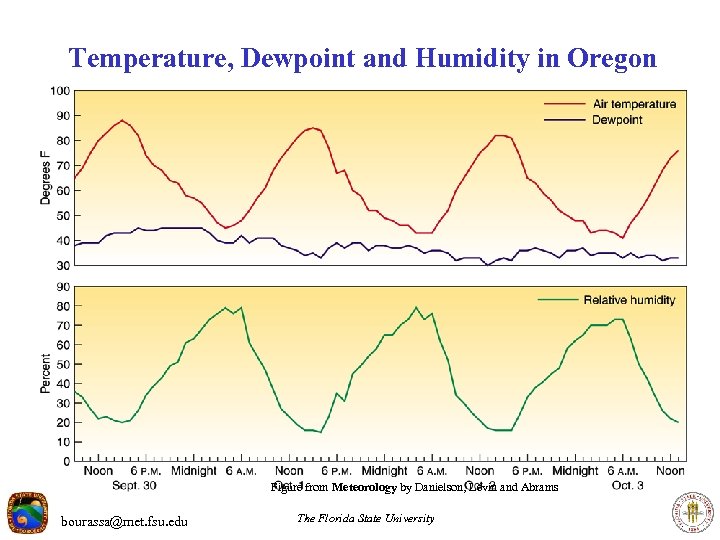Temperature, Dewpoint and Humidity in Oregon Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

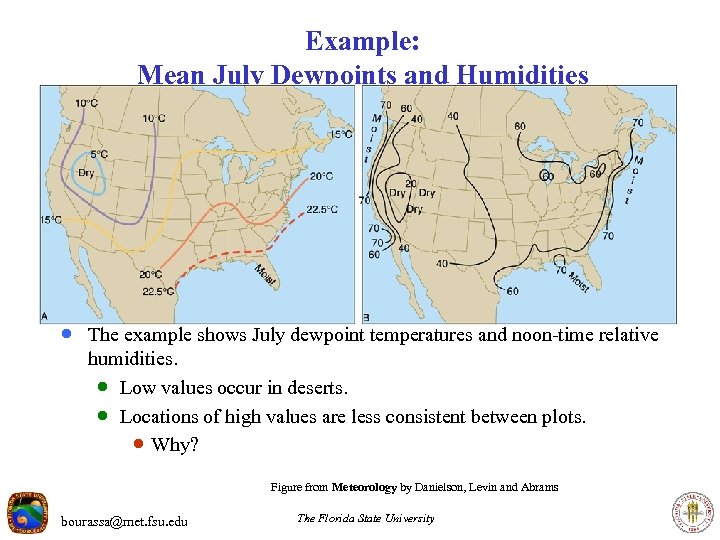Example: Mean July Dewpoints and Humidities · The example shows July dewpoint temperatures and noon-time relative humidities. · Low values occur in deserts. · Locations of high values are less consistent between plots. · Why? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

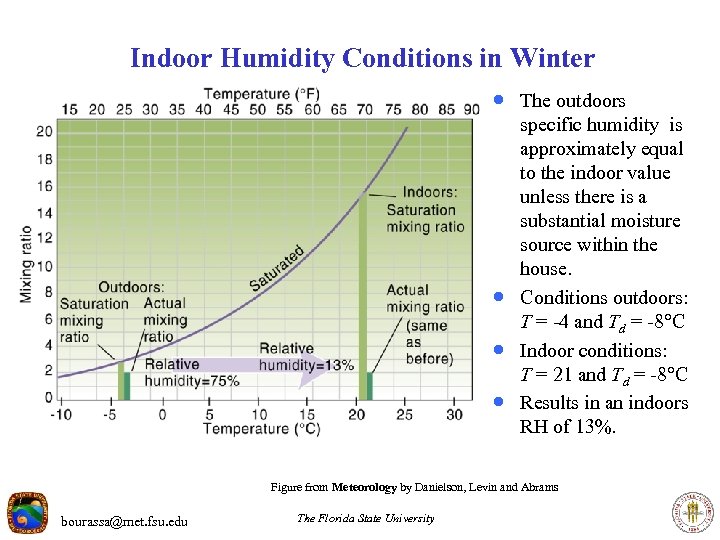Indoor Humidity Conditions in Winter · The outdoors · · · specific humidity is approximately equal to the indoor value unless there is a substantial moisture source within the house. Conditions outdoors: T = -4 and Td = -8 C Indoor conditions: T = 21 and Td = -8 C Results in an indoors RH of 13%. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

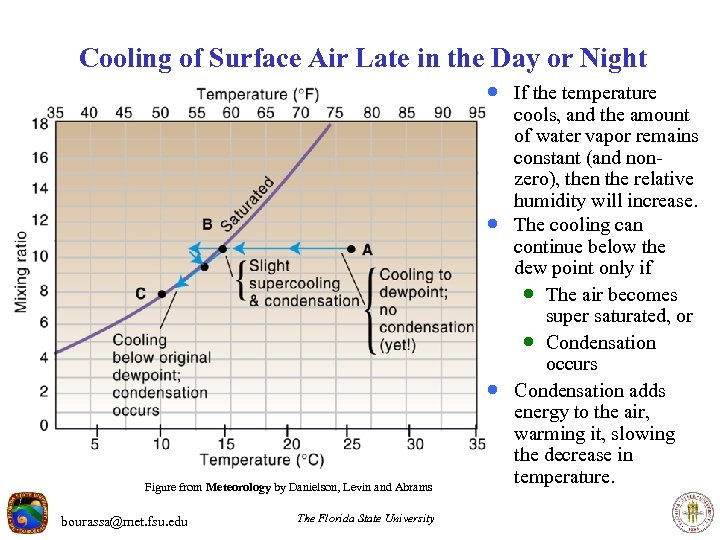Cooling of Surface Air Late in the Day or Night · If the temperature · · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University cools, and the amount of water vapor remains constant (and nonzero), then the relative humidity will increase. The cooling can continue below the dew point only if · The air becomes super saturated, or · Condensation occurs Condensation adds energy to the air, warming it, slowing the decrease in temperature.

Dew and Frost · If the surface temperature decreases below the dew point of the air, then air very near the surface will also cool below the dew point. · Under these conditions, water vapor in the air will condense on the surface, · until a new equilibrium is achieved. The condensed water forms dew. · If the dew point temperature is below freezing, then it could more accurately · be thought of as a frost point. Ice on highways can be a major safety hazard! · It is also a hazard for many plants. · Forecasting occurrences of frost hopefully allows for appropriate preparations. bourassa@met. fsu. edu The Florida State University

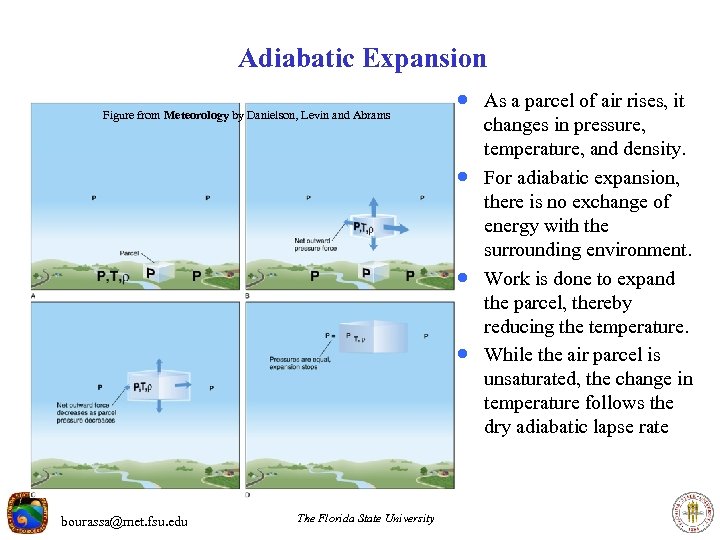Adiabatic Expansion Figure from Meteorology by Danielson, Levin and Abrams · As a parcel of air rises, it · · · bourassa@met. fsu. edu The Florida State University changes in pressure, temperature, and density. For adiabatic expansion, there is no exchange of energy with the surrounding environment. Work is done to expand the parcel, thereby reducing the temperature. While the air parcel is unsaturated, the change in temperature follows the dry adiabatic lapse rate

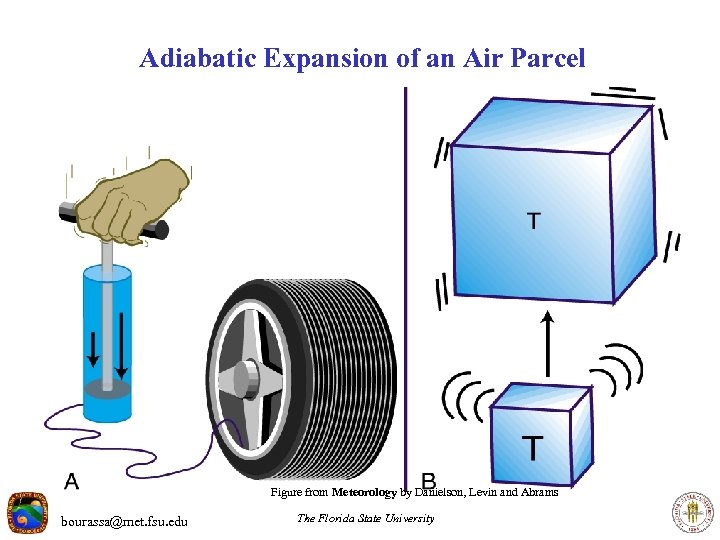Adiabatic Expansion of an Air Parcel Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

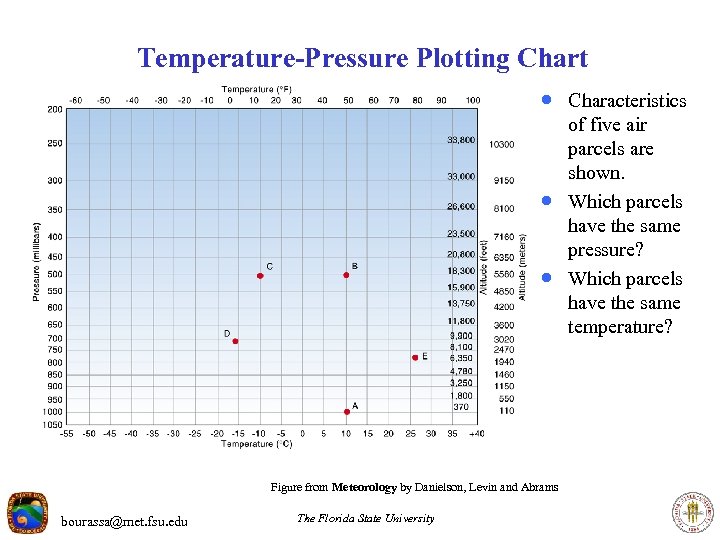Temperature-Pressure Plotting Chart · Characteristics · · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University of five air parcels are shown. Which parcels have the same pressure? Which parcels have the same temperature?

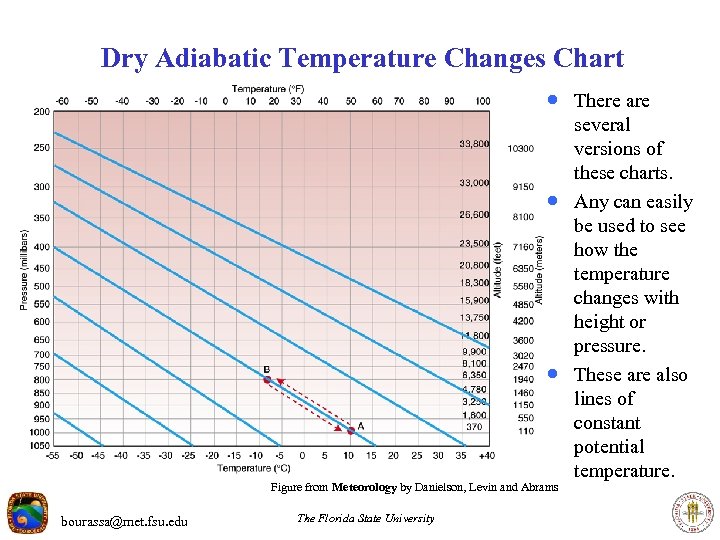Dry Adiabatic Temperature Changes Chart · There are · · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University several versions of these charts. Any can easily be used to see how the temperature changes with height or pressure. These are also lines of constant potential temperature.

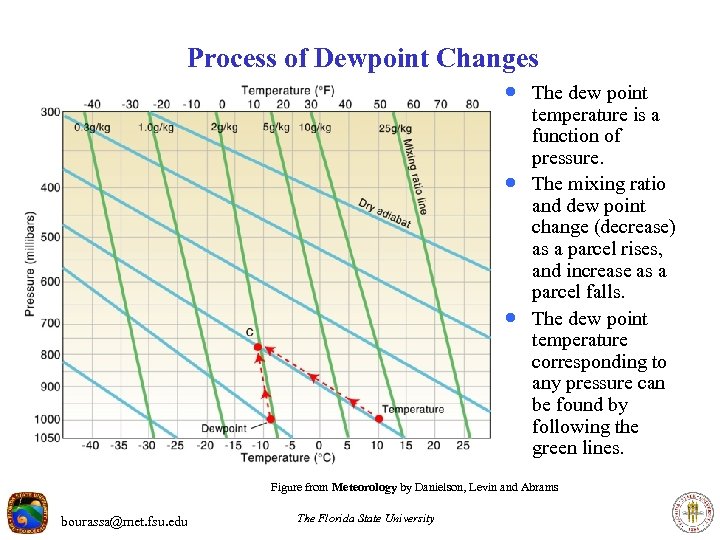Process of Dewpoint Changes · The dew point · · temperature is a function of pressure. The mixing ratio and dew point change (decrease) as a parcel rises, and increase as a parcel falls. The dew point temperature corresponding to any pressure can be found by following the green lines. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

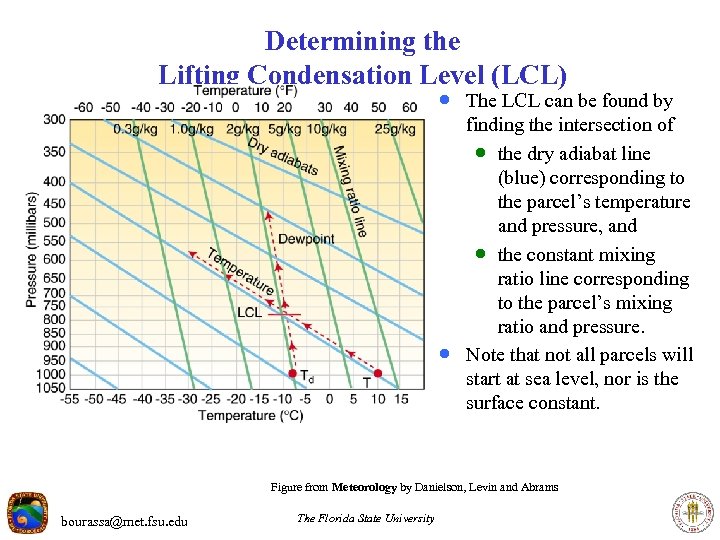Determining the Lifting Condensation Level (LCL) · The LCL can be found by · finding the intersection of · the dry adiabat line (blue) corresponding to the parcel’s temperature and pressure, and · the constant mixing ratio line corresponding to the parcel’s mixing ratio and pressure. Note that not all parcels will start at sea level, nor is the surface constant. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

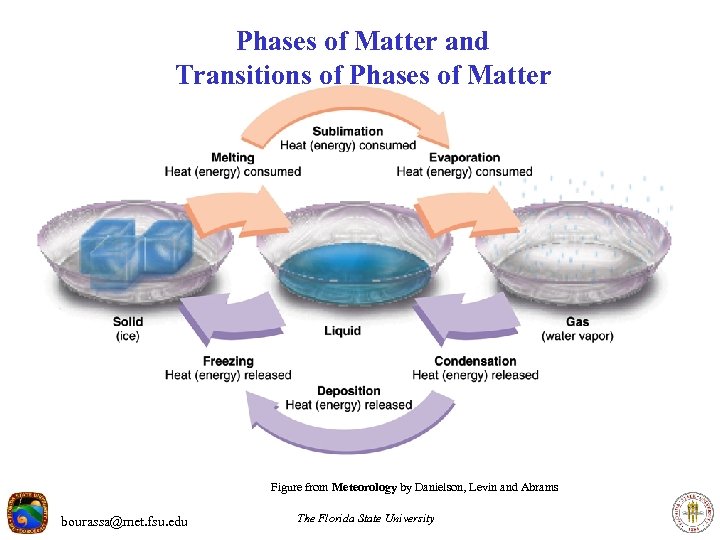Phases of Matter and Transitions of Phases of Matter Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Energy Associated with Phase Changes · Changing phase requires either energy input (melting, sublimation, and evaporation), or releases energy (condensation, deposition, and freezing). · H 2 O examples: · Latent heat of vaporization (evaporation): Lv 2. 258 x 106 J kg-1 · Latent heat of fusion: Lf 3. 34 x 105 J kg-1 · Ignoring other considerations, how much energy is required to change 1 gram of water to water vapor? 1 g H 20 x 1 kg x 2. 258 x 106 J kg-1 = 2. 5 x 103 J =2258 J 1000 g · How much energy is released when the 1 g of water vapor condenses? bourassa@met. fsu. edu The Florida State University

The Moist Adiabatic Lapse Rate · Rising air that is saturated DOES NOT follow the dry adiabat. · Why? · Recall that we determined our dry adiabatic lapse rate by assuming the · change in energy with height is zero. · d(energy) / dz = 0 · Energy = thermal energy + potential energy = Cp. T + gz · - (d. T / dz) = g / Cp 10 C/km The moist adiabatic lapse rate is different because of the input of energy from latent heat release. · - (d. T / dz) = g / Cp - (Lv / Cp) dr/dz · Units check: [d. T / dz] = K m-1 [(Lv / Cp) dr/dz] = (J kg-1) (J-1 K kg) (kg kg-1 m-1) = K m-1 · The moist lapse rate is variable: usually 4 to 7 C/km bourassa@met. fsu. edu The Florida State University

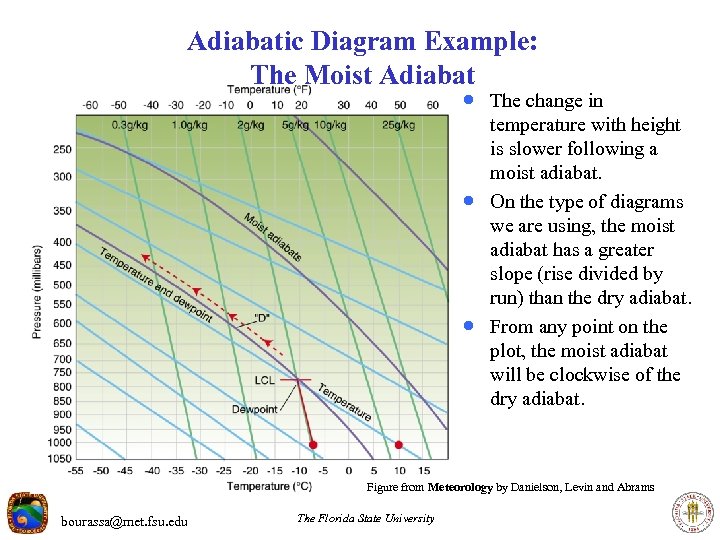Adiabatic Diagram Example: The Moist Adiabat · The change in · · temperature with height is slower following a moist adiabat. On the type of diagrams we are using, the moist adiabat has a greater slope (rise divided by run) than the dry adiabat. From any point on the plot, the moist adiabat will be clockwise of the dry adiabat. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

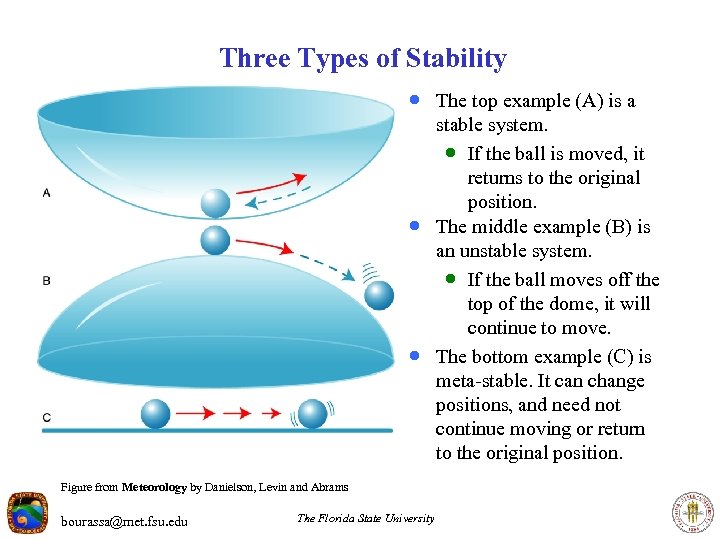Three Types of Stability · The top example (A) is a · · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University stable system. · If the ball is moved, it returns to the original position. The middle example (B) is an unstable system. · If the ball moves off the top of the dome, it will continue to move. The bottom example (C) is meta-stable. It can change positions, and need not continue moving or return to the original position.

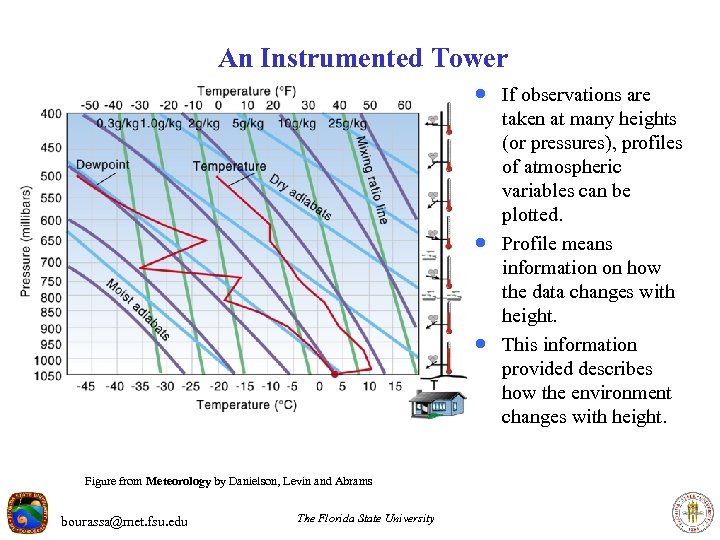An Instrumented Tower · If observations are · · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University taken at many heights (or pressures), profiles of atmospheric variables can be plotted. Profile means information on how the data changes with height. This information provided describes how the environment changes with height.

Environment Temperatures · Another example of environmental · · conditions is an office building. Each room can be thought of as being the local environment. The elevator can move up through the environment. The elevator is analogous to the parcel of air. · It moves up or down through the environment. · The environment does not change when the parcel moves through it. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

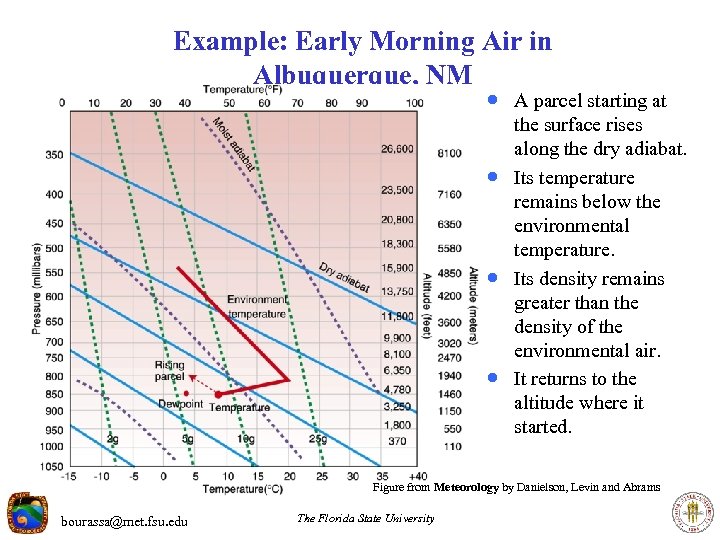Example: Early Morning Air in Albuquerque, NM · A parcel starting at · · · the surface rises along the dry adiabat. Its temperature remains below the environmental temperature. Its density remains greater than the density of the environmental air. It returns to the altitude where it started. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

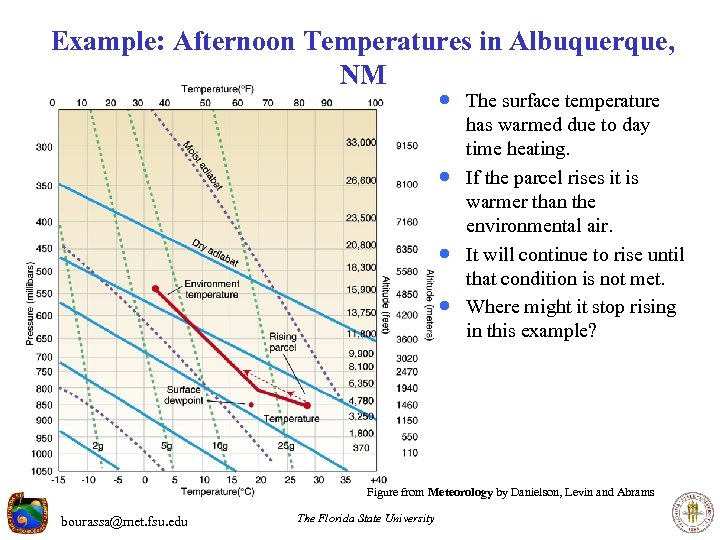Example: Afternoon Temperatures in Albuquerque, NM · The surface temperature · · · has warmed due to day time heating. If the parcel rises it is warmer than the environmental air. It will continue to rise until that condition is not met. Where might it stop rising in this example? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

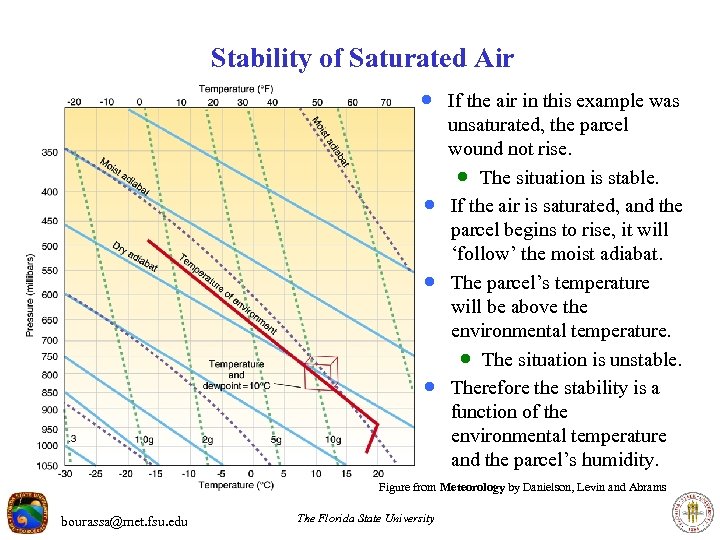Stability of Saturated Air · If the air in this example was · · · unsaturated, the parcel wound not rise. · The situation is stable. If the air is saturated, and the parcel begins to rise, it will ‘follow’ the moist adiabat. The parcel’s temperature will be above the environmental temperature. · The situation is unstable. Therefore the stability is a function of the environmental temperature and the parcel’s humidity. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

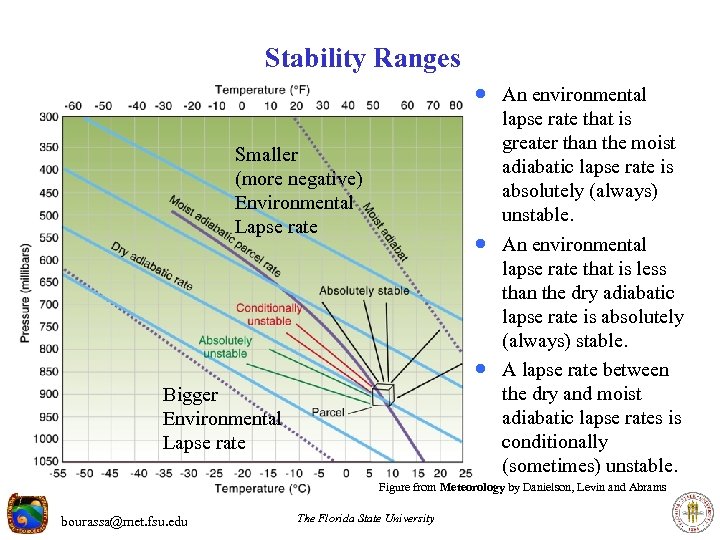Stability Ranges · An environmental lapse rate that is greater than the moist adiabatic lapse rate is absolutely (always) unstable. Smaller (more negative) Environmental Lapse rate · An environmental · Bigger Environmental Lapse rate lapse rate that is less than the dry adiabatic lapse rate is absolutely (always) stable. A lapse rate between the dry and moist adiabatic lapse rates is conditionally (sometimes) unstable. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

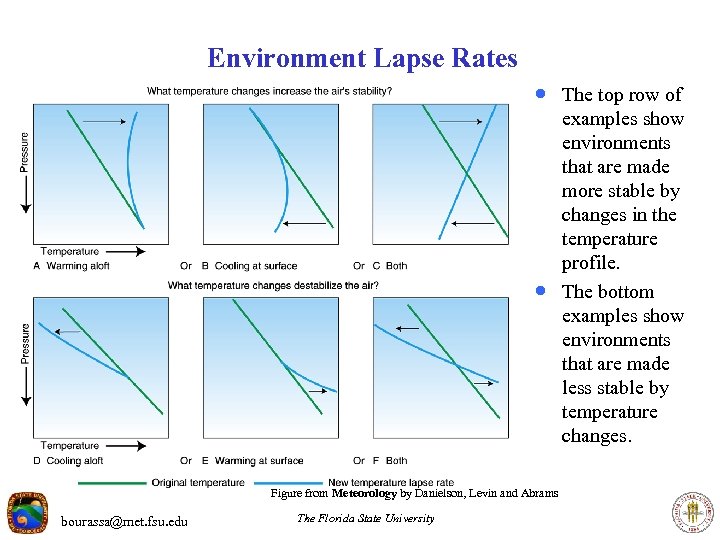Environment Lapse Rates · The top row of · Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University examples show environments that are made more stable by changes in the temperature profile. The bottom examples show environments that are made less stable by temperature changes.

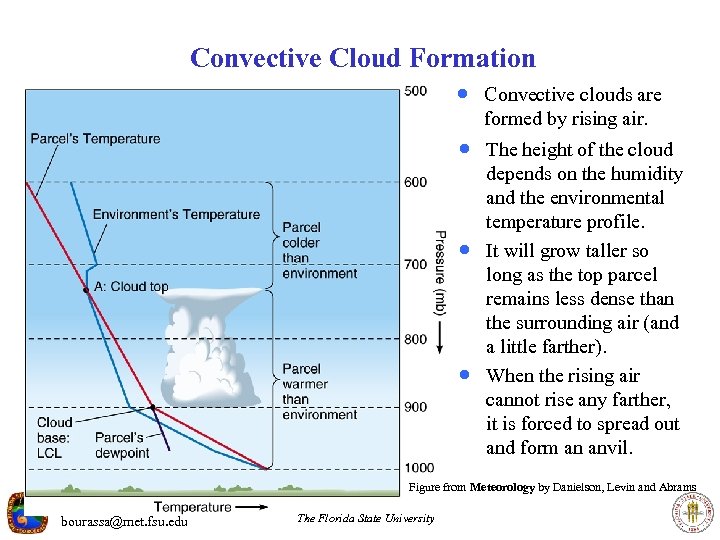Convective Cloud Formation · Convective clouds are formed by rising air. · The height of the cloud · · depends on the humidity and the environmental temperature profile. It will grow taller so long as the top parcel remains less dense than the surrounding air (and a little farther). When the rising air cannot rise any farther, it is forced to spread out and form an anvil. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

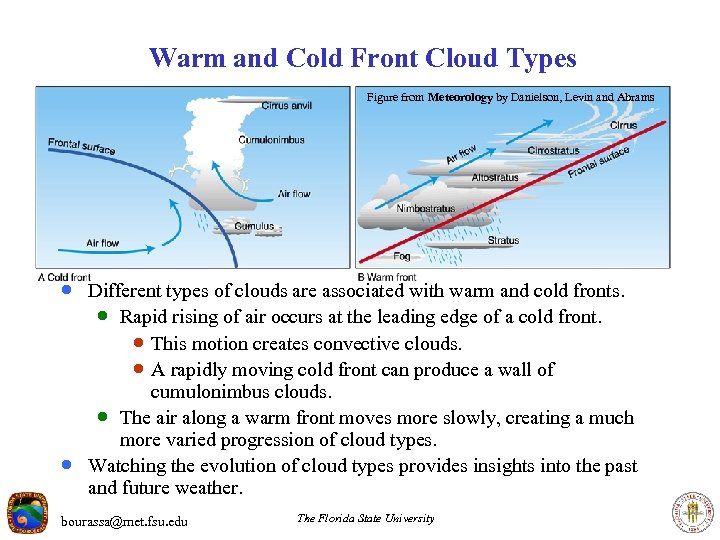Warm and Cold Front Cloud Types Figure from Meteorology by Danielson, Levin and Abrams · Different types of clouds are associated with warm and cold fronts. · Rapid rising of air occurs at the leading edge of a cold front. · This motion creates convective clouds. · A rapidly moving cold front can produce a wall of · cumulonimbus clouds. · The air along a warm front moves more slowly, creating a much more varied progression of cloud types. Watching the evolution of cloud types provides insights into the past and future weather. bourassa@met. fsu. edu The Florida State University

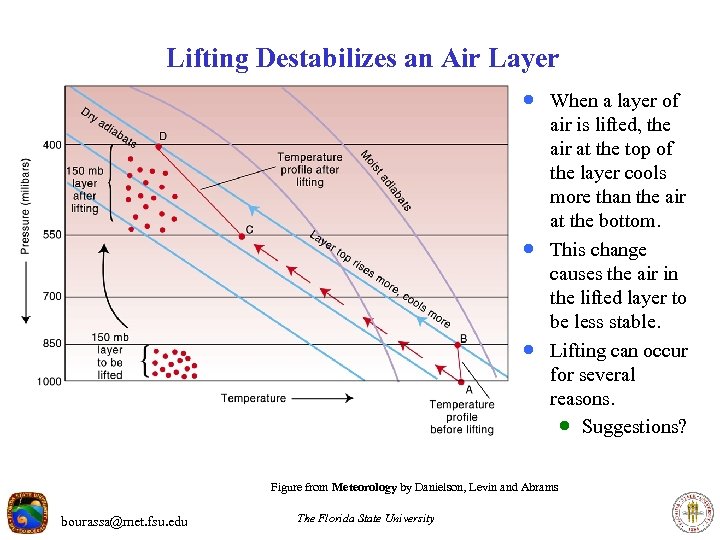Lifting Destabilizes an Air Layer · When a layer of · · air is lifted, the air at the top of the layer cools more than the air at the bottom. This change causes the air in the lifted layer to be less stable. Lifting can occur for several reasons. · Suggestions? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

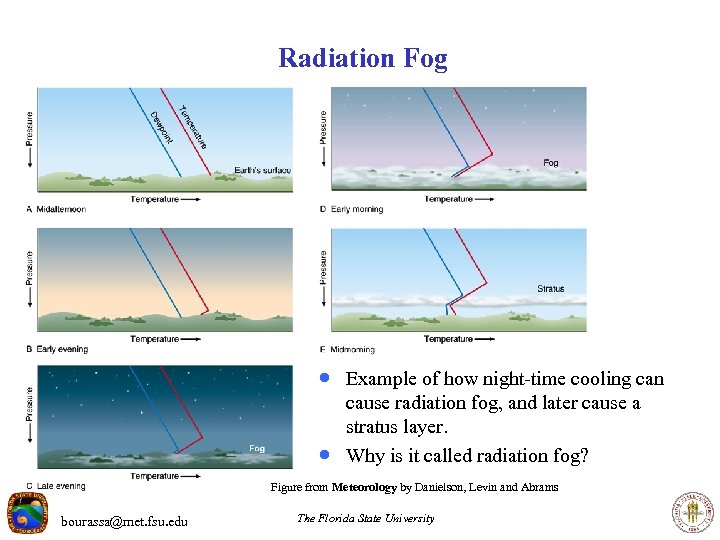Radiation Fog · Example of how night-time cooling can · cause radiation fog, and later cause a stratus layer. Why is it called radiation fog? Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

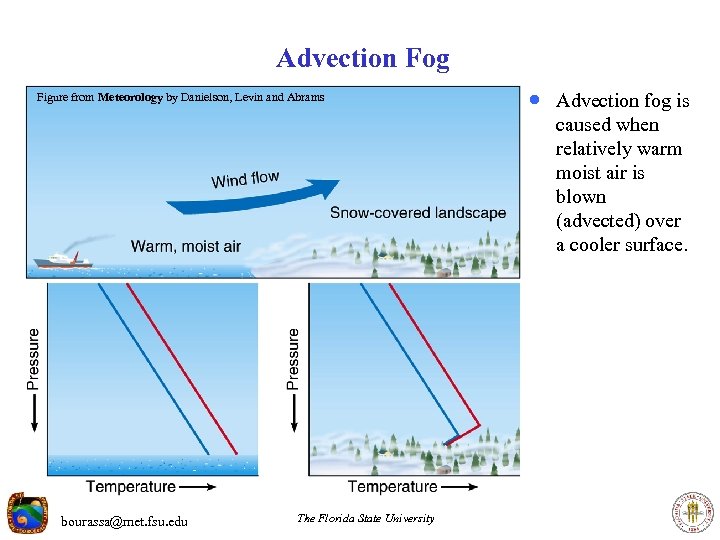Advection Fog Figure from Meteorology by Danielson, Levin and Abrams · Advection fog is caused when relatively warm moist air is blown (advected) over a cooler surface. bourassa@met. fsu. edu The Florida State University

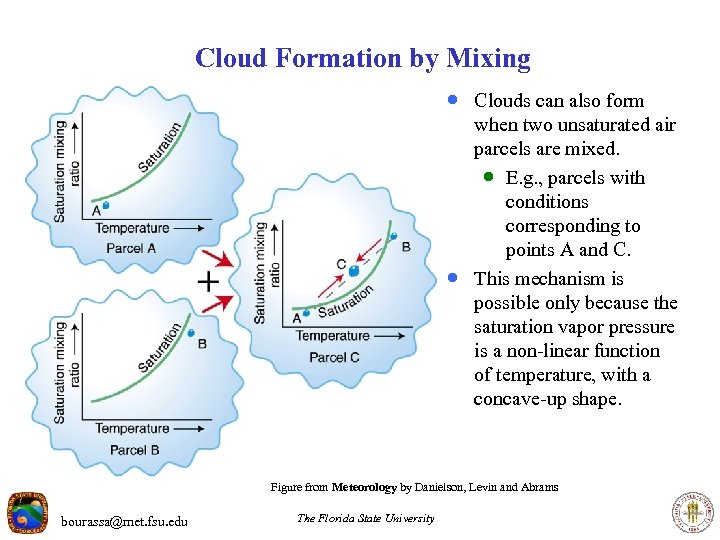Cloud Formation by Mixing · Clouds can also form · when two unsaturated air parcels are mixed. · E. g. , parcels with conditions corresponding to points A and C. This mechanism is possible only because the saturation vapor pressure is a non-linear function of temperature, with a concave-up shape. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

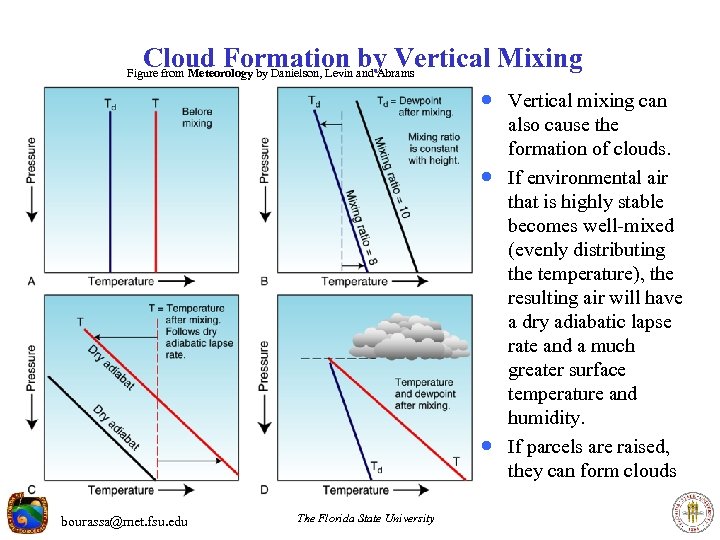Cloud Formation by Vertical Mixing Figure from Meteorology by Danielson, Levin and Abrams · Vertical mixing can · · bourassa@met. fsu. edu The Florida State University also cause the formation of clouds. If environmental air that is highly stable becomes well-mixed (evenly distributing the temperature), the resulting air will have a dry adiabatic lapse rate and a much greater surface temperature and humidity. If parcels are raised, they can form clouds

Examples of Land Sea Breezes · Well known in Classical world · Ancient Greeks took advantage of land breezes to make exiting a port · · easier (with the wind). Sea breeze: surface flow (2) is from the sea. Land breeze: surface flow is (2) from the land. Air rises (3) over the relatively warm surface, and falls (5) over the relatively cool surface. These processes create a circulation. Source: http: //www. islandnet. com/~see/weather/elements/seabrz. htm bourassa@met. fsu. edu The Florida State University

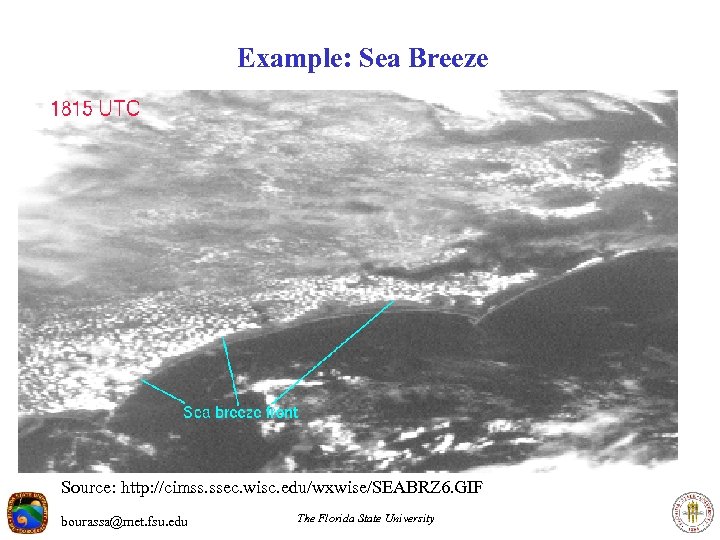Example: Sea Breeze Source: http: //cimss. ssec. wisc. edu/wxwise/SEABRZ 6. GIF bourassa@met. fsu. edu The Florida State University

Land Sea Breeze Circulations · The average condition (Fig. A) shows uniform thickness over land sea. · During the day, the temperature of the · surface will increase more over land than over water. · Both increase (more details on the next slide). The thermal expansion causes an adjustment of the pressure levels, and results in a pressure gradient that aids the return flow towards the cooler surface. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Phases of Matter · In a solid phase, molecules vibrate in place, but cannot move freely. · In a liquid phase, molecules are densely packed (as in solids), but they are · · free to move while remaining in close contact. In the gas phase, molecules move rapidly and freely, and expand to fill their container. Water is a particularly interesting example because three phases can exist together for typical conditions on earth. Graphic from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

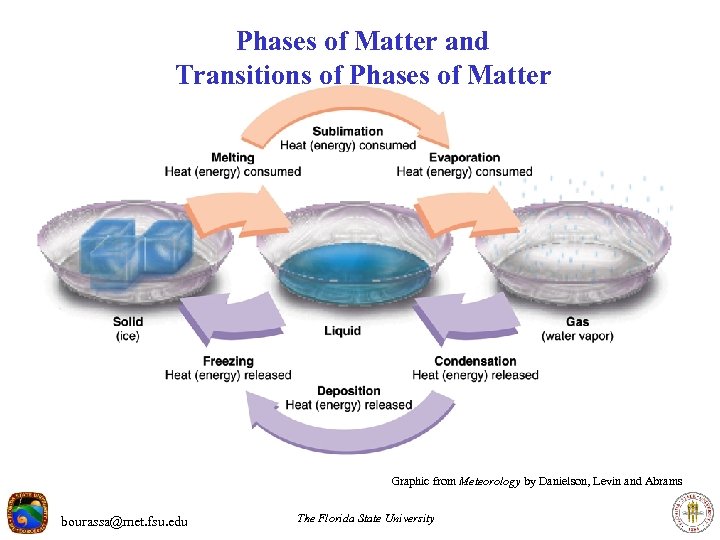Phases of Matter and Transitions of Phases of Matter Graphic from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Energy Associated with Phase Changes · Changing phase requires either energy input (melting, sublimation, and evaporation), or releases energy (condensation, deposition, and freezing). · H 2 O examples: · Latent heat of vaporization (evaporation): Lv 2. 258 x 106 J kg-1 · Latent heat of fusion: Lf 3. 34 x 105 J kg-1 · Ignoring other considerations, how much energy is required to change 1 gram of water to water vapor? 1 g H 20 x 1 kg x 2. 258 x 106 J kg-1 = 2. 258 x 103 J =2258 J 1000 g · How much energy is released when the 1 g of water vapor condenses? bourassa@met. fsu. edu The Florida State University

Examples Related to Rain · Assume (incorrectly) that all · · · bourassa@met. fsu. edu The Florida State University rain came from local water vapor. Rate of energy release per unit area (E) = rain rate * Lv * water Lv 2. 258 x 106 J kg-1 water 1000 kg m-3 (density)

Thermal Energy · The amount of energy required to heat an object depends on the mass · · of the object and the material. · The amount of energy required (or released) per unit mass is the heat capacity (Cp). · Examples: · Water 4217 J kg-1 C-1 · Oxygen (gas) 919 J kg-1 C-1 · Copper 386 J kg-1 C-1 · Nitrogen (gas) 1045 J kg-1 C-1 The heat capacity of a mixture is a mass weighted average of the component molecules. Cp air = sum of “volume fraction * molecular weight * Cp”, summed over each molecular constituent, and divided by the sum of “volume fraction * molecular weight”. The heat capacity of air is · Cp = 1004 J kg-1 C-1 air bourassa@met. fsu. edu The Florida State University

More on Weighted Averages · An unweighted average considers all elements of a set equally. · Let a set of values {x} = x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + … + x. N · The average value of x is · This can also be written with a summation · A weighted average allows some values to be more influential than others. Let w be weights for the set {x} bourassa@met. fsu. edu The Florida State University

Putting It Together (Example) · Example of the energy required to convert 2 kg of ice at 0 C to water vapor · at 150 C. Processes: · Convert ice to water · Heat water to 100 C · Convert water to water vapor · Heat water vapor to 150 C bourassa@met. fsu. edu The Florida State University

Putting It Together (Example) Example of the energy required to convert 2 kg of ice at -20 C to water vapor at 150 C. Processes: · Heat ice to 0 C M * T * Cp = 2 kg * 20 C * 4217 J kg-1 C-1 · Convert ice to water: M * Lf = 2 kg * 3. 34*105 J kg-1 · Heat water to 100 C M * T * Cp = 2 kg * 100 C * 4217 J kg-1 C-1 · Convert water to water vapor M * Lv = 2 kg * 2. 258*106 J kg-1 · Heat water vapor to 150 C M * T * Cp = 2 kg * 50 C * 4217 J kg-1 C-1 where M = mass Lf = latent heat of fusion Lv = latent heat of vaporization bourassa@met. fsu. edu Cp = heat capacity T = change in temperature The Florida State University

Putting It Together (Example) Example of the energy required to convert 2 kg of ice at -20 C to water vapor at 150 C. Processes: · Heat ice to 0 C M * T * Cp = 2 kg * 20 C * 4217 J kg-1 C-1 = 168, 680 J · Convert ice to water: M * Lf = 2 kg * 3. 34*105 J kg-1 = 668, 000 J · Heat water to 100 C M * T * Cp = 2 kg * 100 C * 4217 J kg-1 C-1 = 843, 400 J · Convert water to water vapor M * Lf = 2 kg * 2. 258*106 J kg-1 = = 4, 660, 000 J · Heat water vapor to 150 C M * T * Cp = 2 kg * 50 C * 4217 J kg-1 C-1 = 421, 700 J · For a total of 6, 593, 100 J where M = mass Cp = heat capacity Lf = latent heat of fusion T = change in temperature Lv = latent heat of vaporization bourassa@met. fsu. edu The Florida State University

Change In Temperature With Height (The Lapse Rate) · In meteorology jargon, the rate of change of temperature, as height decreases (-d. T/dz), is called the lapse rate. · For air parcels without any changes in energy due to phase changes of water, or due to radiative heating or cooling, we call the rate of change the dry adiabatic lapse rate. · Dry means that no water vapor is converted to water. · Adiabatic means that there is no exchange of energy with items outside the air parcel. · (energy per unit mass) / z = 0 · Energy per unit mass = thermal energy + potential energy = Cp. T + gz · For infinitely small z this ratio of differences becomes a derivative. · d(Cp. T + gz)/dz = 0 · Cp d. T / dz + g = 0 (treat g and Cp as independent of z) · - (d. T / dz) = g / Cp 10 C/km bourassa@met. fsu. edu The Florida State University

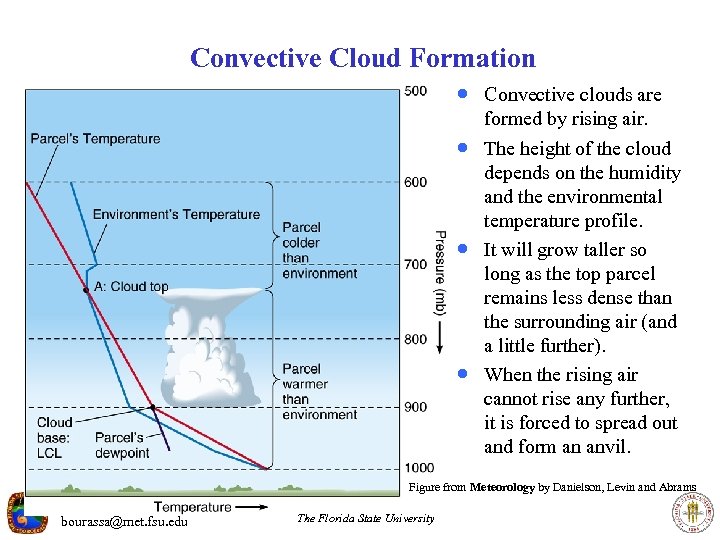Convective Cloud Formation · Convective clouds are formed by rising air. · The height of the cloud · · depends on the humidity and the environmental temperature profile. It will grow taller so long as the top parcel remains less dense than the surrounding air (and a little further). When the rising air cannot rise any further, it is forced to spread out and form an anvil. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

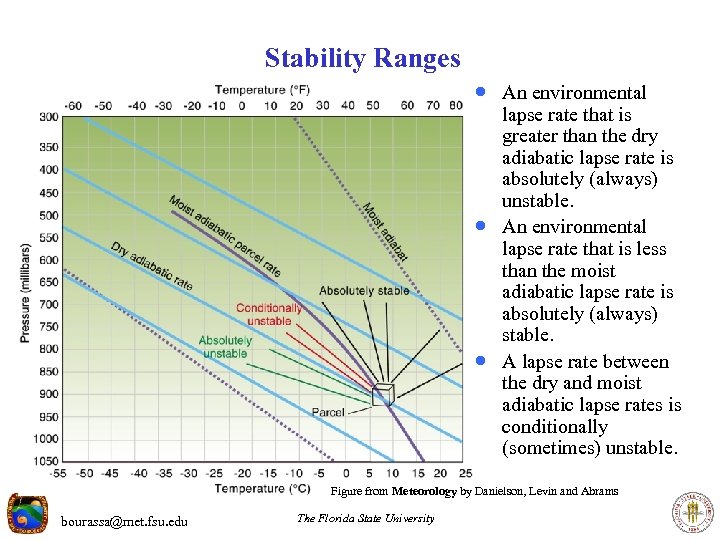Stability Ranges · An environmental · · lapse rate that is greater than the dry adiabatic lapse rate is absolutely (always) unstable. An environmental lapse rate that is less than the moist adiabatic lapse rate is absolutely (always) stable. A lapse rate between the dry and moist adiabatic lapse rates is conditionally (sometimes) unstable. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

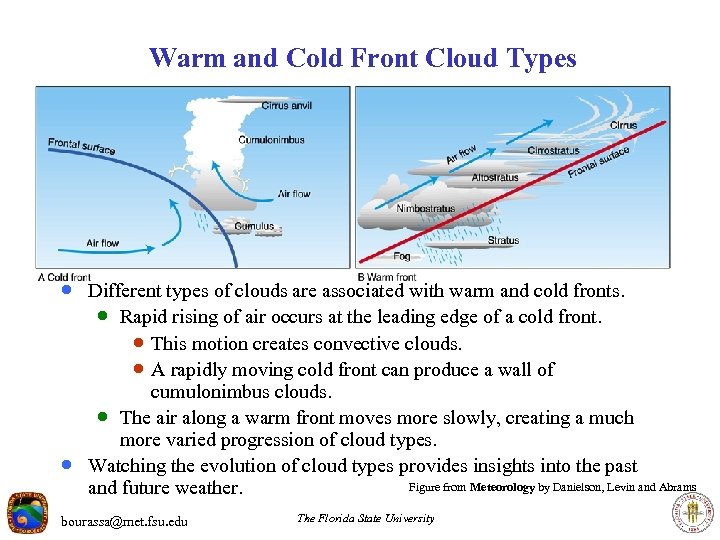Warm and Cold Front Cloud Types · Different types of clouds are associated with warm and cold fronts. · Rapid rising of air occurs at the leading edge of a cold front. · This motion creates convective clouds. · A rapidly moving cold front can produce a wall of · cumulonimbus clouds. · The air along a warm front moves more slowly, creating a much more varied progression of cloud types. Watching the evolution of cloud types provides insights into the past Figure from Meteorology by Danielson, Levin and Abrams and future weather. bourassa@met. fsu. edu The Florida State University

Precipitation (Strict Definition) · Definition: Liquid and solid H 20 that falls and reaches the ground. · Dew and frost do not fall not considered to be precipitation. · Cloud droplets fall too slowly to be considered (and they usually don’t reach the ground) · Virga is not considered precipitation. Rain does not reach the surface. Why doesn’t it reach the surface? bourassa@met. fsu. edu The Florida State University

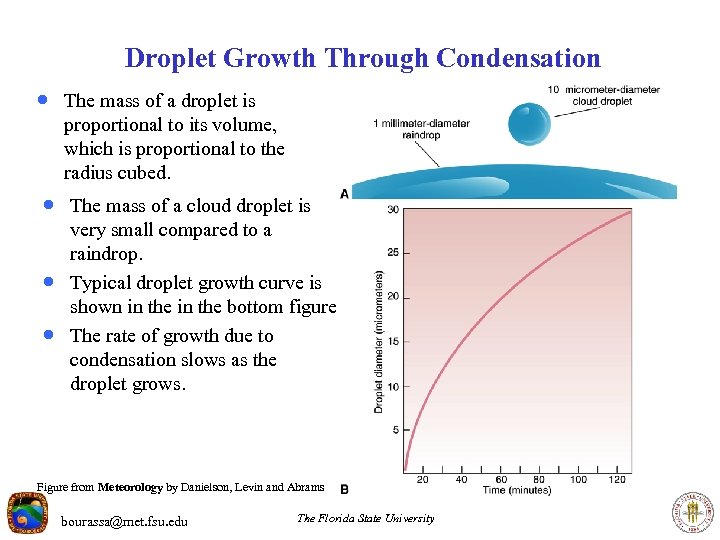Droplet Growth Through Condensation · The mass of a droplet is proportional to its volume, which is proportional to the radius cubed. · The mass of a cloud droplet is · · very small compared to a raindrop. Typical droplet growth curve is shown in the bottom figure. The rate of growth due to condensation slows as the droplet grows. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Growth Through Collision and Coalescence · Collision refers to droplets hitting (colliding) with each other. · Coalescence refers to droplets that have collided sticking together. · Example: if droplets on two fingers are brought close enough together, the two droplets will merge into one droplet. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

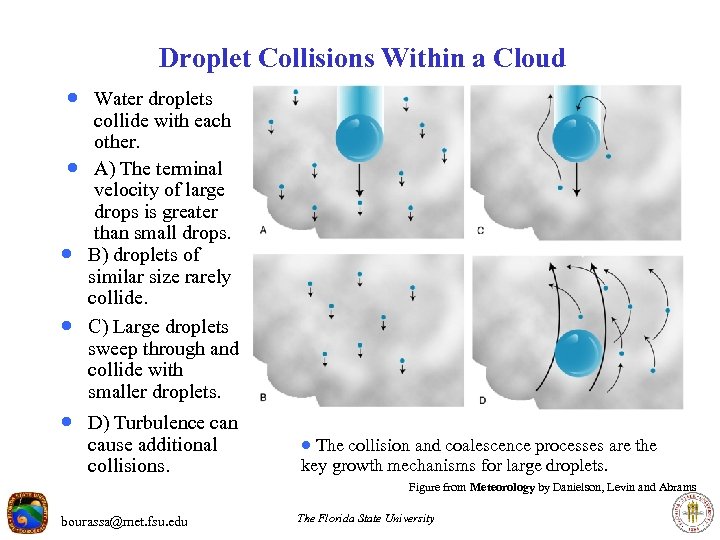Droplet Collisions Within a Cloud · Water droplets · · · collide with each other. A) The terminal velocity of large drops is greater than small drops. B) droplets of similar size rarely collide. C) Large droplets sweep through and collide with smaller droplets. · D) Turbulence can cause additional collisions. · The collision and coalescence processes are the key growth mechanisms for large droplets. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Coalescence · Collision efficiency (E) = # drops collide _ # of droplets in path · Some droplets that collide do not stick. · Coalescence efficiency = # of droplets coalesced · # of drops that collided Ochs et al. (1986) measured laboratory coalescence efficiencies for collector drops with radii between 128 and 300 microns and found that the coalescence efficiency decreased from 1. 0 to 0. 39 as the ratio of the collected to collector drop radii decreased. · Collection efficiency = Coalescence efficiency * Collision efficiency bourassa@met. fsu. edu The Florida State University

Raindrop Breakup · Small Raindrops and droplets are approximately round. · These are quite stable. · Relatively large rain drops tend to distort (when falling) more than small drops. · In extreme cases, they can become almost doughnut shaped · Raindrops that are greater than 5 mm will break up as they fall. bourassa@met. fsu. edu The Florida State University

How Important is Collision and Coalescence? · Collision & Coalescence is the dominant process in warm clouds. · Warm clouds have cloud temperatures greater than freezing. · However, warm cloud precipitation is rare – particularly in mid and high latitudes. · Most precipitating clouds have a portion of their volume with temperatures below freezing. bourassa@met. fsu. edu The Florida State University

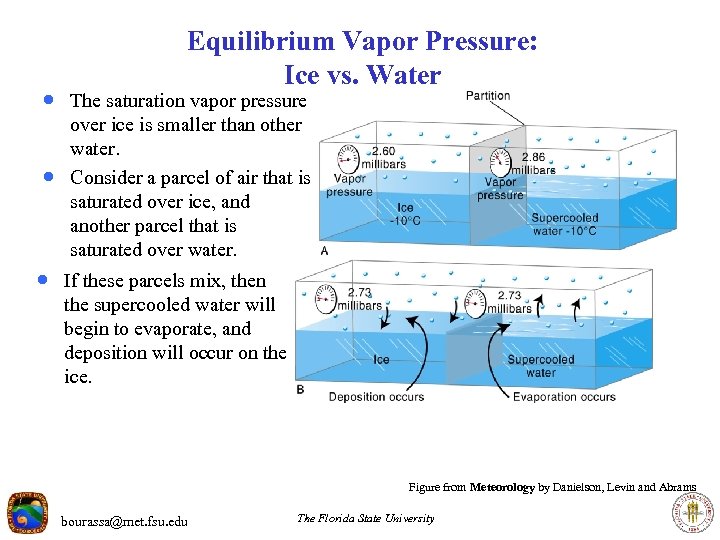Equilibrium Vapor Pressure: Ice vs. Water · The saturation vapor pressure · over ice is smaller than other water. Consider a parcel of air that is saturated over ice, and another parcel that is saturated over water. · If these parcels mix, then the supercooled water will begin to evaporate, and deposition will occur on the ice. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

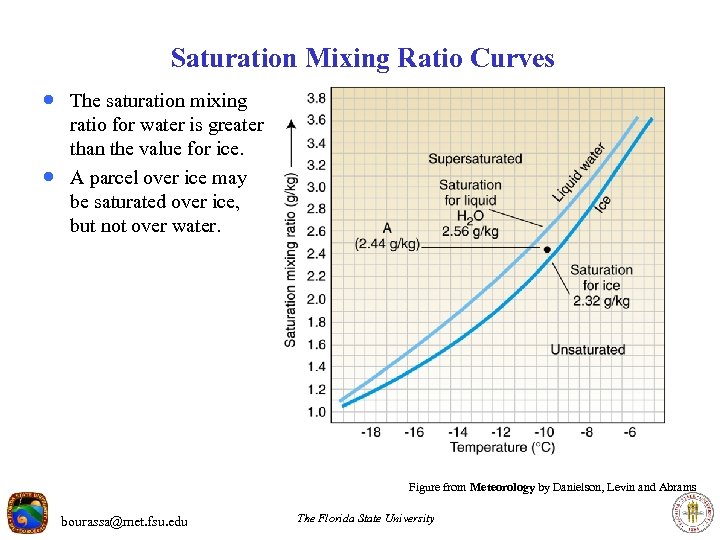Saturation Mixing Ratio Curves · The saturation mixing · ratio for water is greater than the value for ice. A parcel over ice may be saturated over ice, but not over water. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University

Precipitation Formation: Bergeron-Findeisen Process · The Bergeron Process is the · in-cloud formation of ice particles from supercooled water droplets. Supercooled water evaporates, and is then deposited on the ice crystals. Figure from Meteorology by Danielson, Levin and Abrams bourassa@met. fsu. edu The Florida State University