ICTSA Programming Contest 2009 Legal Cheating in Elections

ICTSA Programming Contest 2009 Legal Cheating in Elections Gordon Pace Claudia Borg Chris Porter

Legal Cheating n District boundary manipulation to give an unfair advantage, or gerrymandering has a long history… q 1812: Governor Elbridge Gerry in Massachusetts drew up a district so distorted geographically, that it was likened to a salamander – ‘better call it a gerrymander’ someone commented!

Legal Cheating

Legal Cheating n n Gerrymandering works through the wasted vote effect. Why do we not use a more effective electoral system? Arrow’s impossibility theorem from 1951 demonstrates that no voting system can convert individual rankings into a global one – there can be no fair election system.

An Example

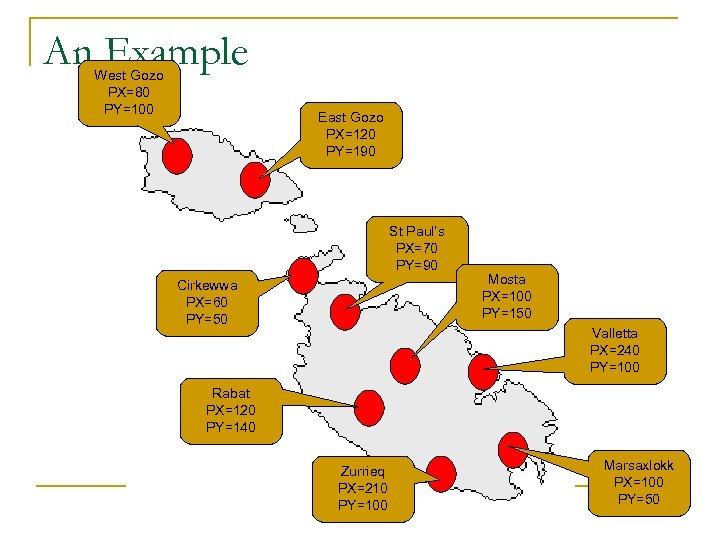An Example West Gozo PX=80 PY=100 East Gozo PX=120 PY=190 St Paul’s PX=70 PY=90 Cirkewwa PX=60 PY=50 Mosta PX=100 PY=150 Valletta PX=240 PY=100 Rabat PX=120 PY=140 Zurrieq PX=210 PY=100 Marsaxlokk PX=100 PY=50

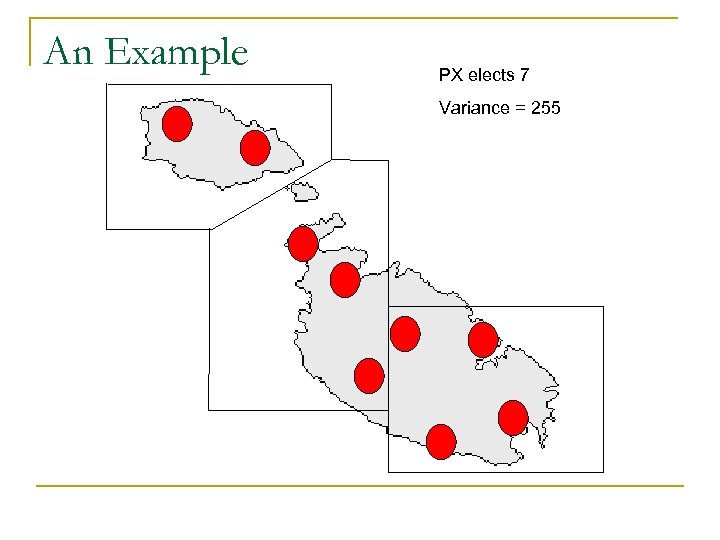An Example PX elects 7 Variance = 255

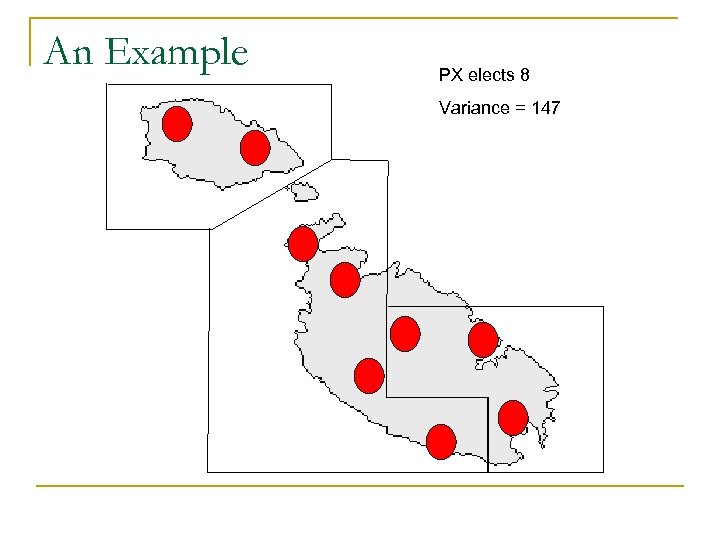An Example PX elects 8 Variance = 147

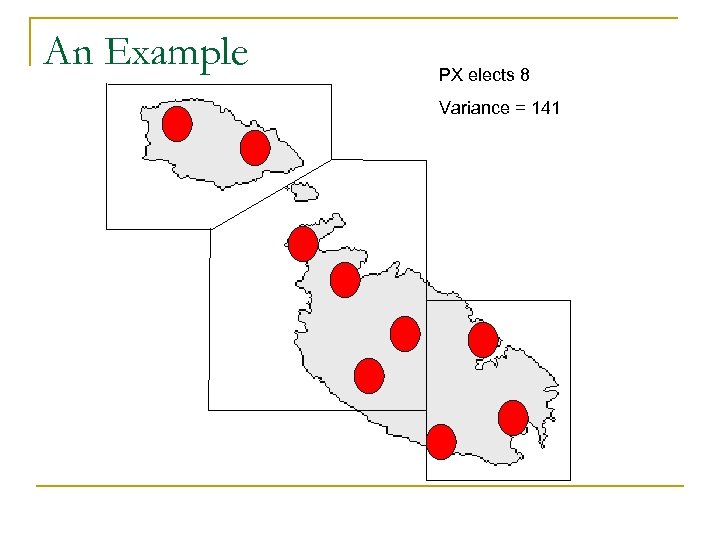An Example PX elects 8 Variance = 141

The Programming Task n Given: q q n A set of villages Connections between villages Expected voting preferences in each village for the two parties PX and PY Number of districts to have To return in less than 5 minutes: q A district partitioning such that districts are connected components

The Programming Task n A good partition is one which: q q n Maximises the number of seats il-Partit tax. Xurbana (PX) elects; and Minimises the differences in populations across districts. Ideally there would have been: q q A bound on the difference between district populations; A bound on the distance between villages in a single district.

How to Solve It n n n The problem can be shown to be NPcomplete (eg via the Knapsack problem). A brute-force solution will only work for small instances. Larger problems require the use of some search heuristic.

The Teams 1. Beeef • Alessio Magro • Reuben Bartolo • Jonathan Caruana 2. Unicus • Gianluca Valentino 3. WM • James Scicluna • Kevin Falzon • Ingram Bondin • Andrew Gauci 4. i. Like • Andrew Borg Cardona • Michael Debono 5. Eat Your Apple! • David Bailey • Andrew Calleja • Alan Cassar • Stephen Fenech 6. dot • Marco Muscat • Joseph Borg 7. HND 4 • Norbert De. Bono • Matthew Xuereb • Andrew Vella 8. CG • Andrew Said 9. Village People • Darren Demicoli

The Teams Solutions: Beeef n n n Genetic Algorithm: using only selection and mutation (crossover did not give better results). Chromosome representation: consist of a list of districts, which in turn are composed of a list of villages. Creation: ensures that: q All the villages in a district must belong to the same `island'. q Districts must be connected. Mutation: works by selecting two districts at random and swapping two villages across: q The two districts must belong to the same `island'. q Check that connectivity is not lost by the addition or the removal. Fitness function: Number of PX members elected, variance. Termination: upon convergence.

The Teams Solutions: Unicus n Heuristic based: The generator worked as follows, repeating as necessary. q Repeat a number of times: n n q q Identified the village where PX has the largest majority and population and place in District 1. Identified the village with the largest PY majority and second largest population, and the village with the second largest PX majority and 3 rd largest population, both of which had to be connected to each other, and placed them in District 2. Create a district with the villages with the largest PX and PY majority, and repeat to use up the remaining villages. Repeat this process for all permutations. Programmed in C using. NET 2. 0

The Teams Solutions: WM n n Special case scenarios, a brute-force search and a Montecarlo method were implemented one of which is chosen depending on the problem given. For non-special cases, a measure of the complexity of the graph is estimated and depending on this one of the solutions is chosen based on benchmarking. q q n Approach 1: Fully enumerative approach, resembling brute force, but with immediate pruning of some impossible candidate solutions Approach 2: An adaptive Montecarlo based approach with generation of results through analysis of the given accident space and appropriate ranking of resulting candidate solutions A timer ensures a solution in the allotted 5 minutes.

The Teams Solutions: i. Like n n Random search: A modified Monte Carlo method, taking features from genetic algorithms Chromosome: District configurations Random generation: Generates random distribution of villages (randomising villages, and placing random separators), and checked for validity Selection: q q n Fitness: More elected PX MPs or better variance is preferred. Validity: Checked later for performance reasons Stopping criteria: 100 generations or reaching a long enough plateau (dependant on size of the problem)

The Teams Solutions: Eat Your Apple! n Preprocessing: q q n n Split the country into separate islands Each island (based on its population) is assigned a number of districts to be allocated within it. Phase 1: Clustering Algorithm q On each island a clustering algorithm groups villages into districts such that the number of elected PX candidates is maximized. q Starts off a random village, and adds others clustered around the initial village. Phase 2: Genetic Algorithm q A genetic algorithm is applied on the output of the clustering algorithm to generate fitter solutions q Fitness function was global maximization of PX candidate count and a globally minimized PY candidate count. q Assigning more weight to the PX count gave better results.

The Teams Solutions: . (dot, tikka) n Preprocessing: Splits the problem into 'islands' to support disconnected nodes. n Genetic algorithm q q Generation: using random starting village and generate a connected district with a modified BFS search. Fitness function: Number of PX members elected and variance

The Teams Solutions: HND 4 n n n Developed using C# on. NET framework 2. 0 Preprocessing: Separate into different islands. Heuristic search: q q Grouping villages where PY dominates and group them in one district if possible If more districts are still required PX dominant districts are divided into smaller ones.

The Teams Solutions: CG n n Calculate all possible district sizes For each possible combination of sizes: q q q n A district is created starting from a village and proceeding in a BFS manner. Try to create the remaining districts ensuring no overlap. Remember the best solution found. Would have liked to add: q q Heuristics to merge villages in a pre-analysis phase eg PYstrong villages close to each other. Use a timer to ensure giving results on time.

The Teams Solutions: Village People n n n Genetic algorithm coded in C Chromosome representation: partitions with connected villages Crossover: injects a district into the chromosone Mutation: randomly assigns a village to a district Genetic repair: is used to ensure that the partitions are still valid Fitness function: Sum of the ratio of members elected of party X against party Y, and the inverse of the variance.

The Test Problems n Set of properties specified for 17 fictitious countries. n Each village has: q 300 ≤ Voters ≤ 500 n q The ratio between the votes for the parties PX: PY was allowed to could range between 20: 80 and 80: 20 n q n Generated randomly before the contest A number of regular map layouts were used. The number of district was chosen so as to ensure an average of 4 villages per district.

The Test Problems 8 grid countries: 3 x 3 to 10 x 10 198, 264 Asgvvjfcne 129, 187 Lczktvafoj 187, 120 Ciioesvamf 175, 144 Szoxxldneo 267, 144 Moawloiblf 232, 232 Kazucjrgqf 220, 91 Lltrdabguo 218, 179 Tgxgmzcaqw 354, 106 Hmxfstqddp

The Test Problems 3 full-mesh grid countries: 3 x 3, 7 x 7, 10 x 10 198, 264 Asgvvjfcne 129, 187 Lczktvafoj 187, 120 Ciioesvamf 175, 144 Szoxxldneo 267, 144 Moawloiblf 232, 232 Kazucjrgqf 220, 91 Lltrdabguo 218, 179 Tgxgmzcaqw 354, 106 Hmxfstqddp

The Test Problems 3 circular countries with 10, 20 and 50 villages 198, 264 Asgvvjfcne 175, 144 168, 156 Szoxxldneo Yisfhxnfvz 129, 187 84, 266 Lczktvafoj Imutautvmw 187, 120 214, 285 Ciioesvamf Wdyvaxlzyb 165, 309 Lvjanqoway 174, 190 200, 227 Vvjzivqcmq Xasfeuqsyp

The Test Problems 3 circular countries with a hub sizes 10, 20 and 50 198, 264 Asgvvjfcne 175, 144 168, 156 Szoxxldneo Yisfhxnfvz 129, 187 84, 266 Lczktvafoj Imutautvmw 74, 263 Dastautvmw 187, 120 214, 285 Ciioesvamf Wdyvaxlzyb 165, 309 Lvjanqoway 174, 190 200, 227 Vvjzivqcmq Xasfeuqsyp

The Test Problem The biggest problem of them all

The Test Problem The biggest problem of them all Malta

The Test Problem: Malta

The Test Problem: Malta n An example from real-life: Malta q q 69 villages Connectivity based on geographical proximity Vote distribution based on the results of the last local elections (2006 – 2008)1 13 districts 1 taken from http: //www. maltadata. com/tr-count 1. htm

The Results: Grids [3 x 3] Beeef 3 x 3 11 829. 54 Unicus N/A WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 829. 54 HND 4 8 860. 24 CG Village People 11 829. 54

The Results: Grids [4 x 4] Beeef Unicus 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 CG Village People 860. 24 11 829. 54 10 1246. 64 14 1385. 91 14 1557. 84 HND 4

The Results: Grids [5 x 5] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26

The Results: Grids [6 x 6] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26 6 x 6 INVALID N/A 33 3182. 35 TIMEOUT 32 2932. 91 30 545. 97 23 3596. 41 TIMEOUT 29 1583. 77

The Results: Grids [7 x 7] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26 6 x 6 INVALID N/A 33 3182. 35 TIMEOUT 32 2932. 91 30 545. 97 23 3596. 41 TIMEOUT 29 1583. 77 7 x 7 INVALID N/A 43 1670. 34 TIMEOUT 42 1158. 84 30 2862. 67 TIMEOUT 39 2655. 99

The Results: Grids [8 x 8] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26 6 x 6 INVALID N/A 33 3182. 35 TIMEOUT 32 2932. 91 30 545. 97 23 3596. 41 TIMEOUT 29 1583. 77 7 x 7 INVALID N/A 43 1670. 34 TIMEOUT 42 1158. 84 30 2862. 67 TIMEOUT 39 2655. 99 8 x 8 45 1286. 76 N/A 51 3200. 13 TIMEOUT 47 759. 37 41 3921. 77 TIMEOUT INVALID

The Results: Grids [9 x 9] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26 6 x 6 INVALID N/A 33 3182. 35 TIMEOUT 32 2932. 91 30 545. 97 23 3596. 41 TIMEOUT 29 1583. 77 7 x 7 INVALID N/A 43 1670. 34 TIMEOUT 42 1158. 84 30 2862. 67 TIMEOUT 39 2655. 99 8 x 8 45 1286. 76 N/A 51 3200. 13 TIMEOUT 47 759. 37 41 3921. 77 TIMEOUT INVALID 9 x 9 58 921. 59 N/A 64 2627. 06 TIMEOUT 61 647. 30 51 3848. 34 TIMEOUT INVALID

The Results: Grids [10 x 10] Beeef Unicus WM i. Like Eat Your Apple! Dot 11 829. 54 11 1081. 46 11 826. 54 8 CG Village People 860. 24 11 829. 54 HND 4 3 x 3 11 829. 54 N/A 4 x 4 13 743. 72 N/A 15 2126. 26 14 2045. 46 14 1855. 38 14 1201. 70 10 1246. 64 14 1385. 91 14 1557. 84 5 x 5 20 628. 31 N/A 24 2462. 99 23 2346. 45 21 1759. 58 21 488. 39 22 1644. 56 TIMEOUT 22 2086. 26 6 x 6 INVALID N/A 33 3182. 35 TIMEOUT 32 2932. 91 30 545. 97 23 3596. 41 TIMEOUT 29 1583. 77 7 x 7 INVALID N/A 43 1670. 34 TIMEOUT 42 1158. 84 30 2862. 67 TIMEOUT 39 2655. 99 8 x 8 45 1286. 76 N/A 51 3200. 13 TIMEOUT 47 759. 37 41 3921. 77 TIMEOUT INVALID 9 x 9 58 921. 59 N/A 64 2627. 06 TIMEOUT 61 647. 30 51 3848. 34 TIMEOUT INVALID 10 x 10 71 1477. 11 N/A 77 3028. 64 TIMEOUT 77 884. 98 74 4552. 36 TIMEOUT 73 2022. 64

The Results: Grids+Diagonal [3 x 3] Beeef 3 x 3 7 Unicus N/A 645. 46 WM 7 i. Like 7 643. 58 646. 30 Eat Your Apple! 7 1258. 76 Dot 6 36. 40 HND 4 5 1163. 59 CG 7 Village People 7 719. 40 645. 46

The Results: Grids+Diagonal [7 x 7] Beeef 3 x 3 7 x 7 7 Unicus N/A 645. 46 35 895. 96 WM 7 7 643. 58 N/A i. Like 42 2153. 71 646. 30 TIMEOUT Eat Your Apple! Dot 7 1258. 76 6 TIMEOUT HND 4 CG 7 36. 40 5 1163. 59 40 1111. 75 45 3749. 09 TIMEOUT Village People 7 719. 40 645. 46 39 2693. 27

The Results: Grids+Diagonal [10 x 10] Beeef 3 x 3 7 Unicus N/A 645. 46 WM 7 i. Like 7 643. 58 646. 30 Eat Your Apple! Dot 7 1258. 76 6 HND 4 CG 7 36. 40 5 1163. 59 Village People 7 719. 40 645. 46 7 x 7 35 895. 96 N/A 42 2153. 71 TIMEOUT 40 1111. 75 45 3749. 09 TIMEOUT 39 2693. 27 10 x 10 70 1352. 75 N/A 75 4132. 35 TIMEOUT 72 477. 99 82 5560. 82 TIMEOUT 69 1917. 86

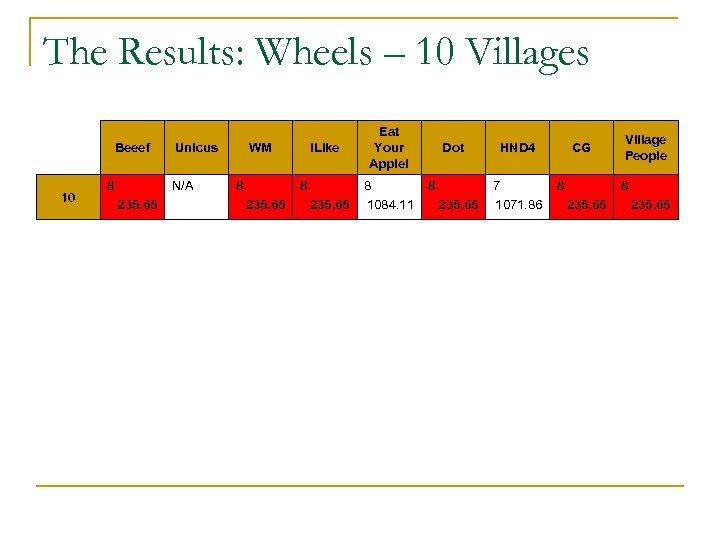The Results: Wheels – 10 Villages Beeef 10 8 Unicus N/A 235. 65 WM 8 i. Like 8 235. 65 Eat Your Apple! 8 1084. 11 Dot 8 235. 65 HND 4 7 1071. 86 CG 8 Village People 8 235. 65

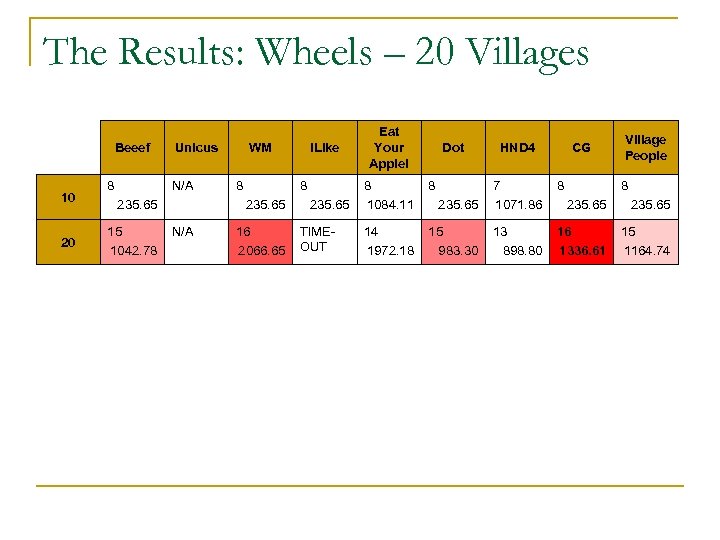The Results: Wheels – 20 Villages Beeef 10 20 8 Unicus N/A 235. 65 15 1042. 78 WM 8 8 235. 65 N/A i. Like 16 2066. 65 235. 65 TIMEOUT Eat Your Apple! Dot 8 1084. 11 8 14 1972. 18 HND 4 CG Village People 8 235. 65 7 1071. 86 8 235. 65 15 983. 30 13 898. 80 16 1336. 61 15 1164. 74

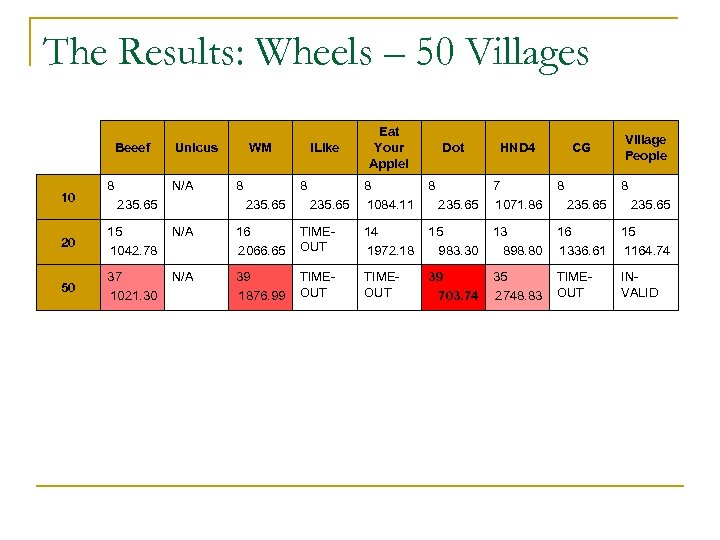The Results: Wheels – 50 Villages Beeef 10 8 Unicus N/A 235. 65 WM 8 i. Like 8 235. 65 Eat Your Apple! Dot 8 1084. 11 8 HND 4 CG Village People 8 235. 65 7 1071. 86 8 235. 65 20 15 1042. 78 N/A 16 2066. 65 TIMEOUT 14 1972. 18 15 983. 30 13 898. 80 16 1336. 61 15 1164. 74 50 37 1021. 30 N/A 39 1876. 99 TIMEOUT 39 703. 74 35 2748. 83 TIMEOUT INVALID

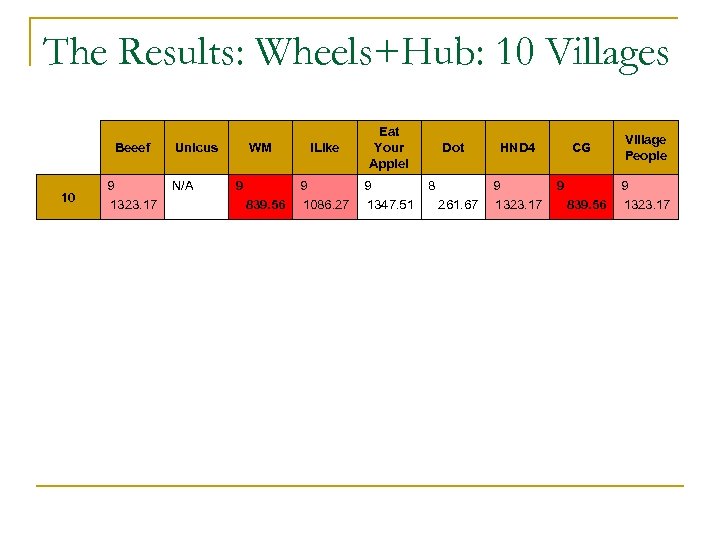The Results: Wheels+Hub: 10 Villages Beeef 10 9 1323. 17 Unicus N/A WM 9 839. 56 i. Like Eat Your Apple! 9 1086. 27 9 1347. 51 Dot 8 261. 67 HND 4 9 1323. 17 CG 9 839. 56 Village People 9 1323. 17

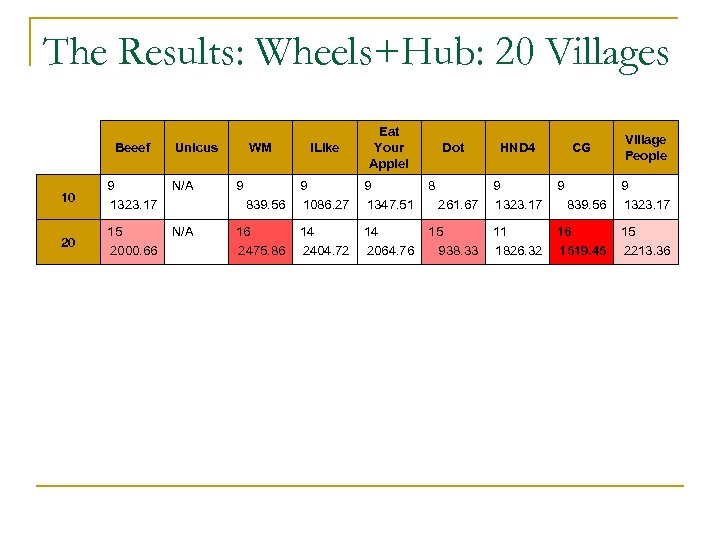The Results: Wheels+Hub: 20 Villages Beeef i. Like Eat Your Apple! 9 1347. 51 8 839. 56 9 1086. 27 16 2475. 86 14 2404. 72 14 2064. 76 Unicus 10 9 1323. 17 N/A 20 15 2000. 66 N/A WM 9 Dot HND 4 CG Village People 9 261. 67 9 1323. 17 839. 56 9 1323. 17 15 938. 33 11 1826. 32 16 1519. 45 15 2213. 36

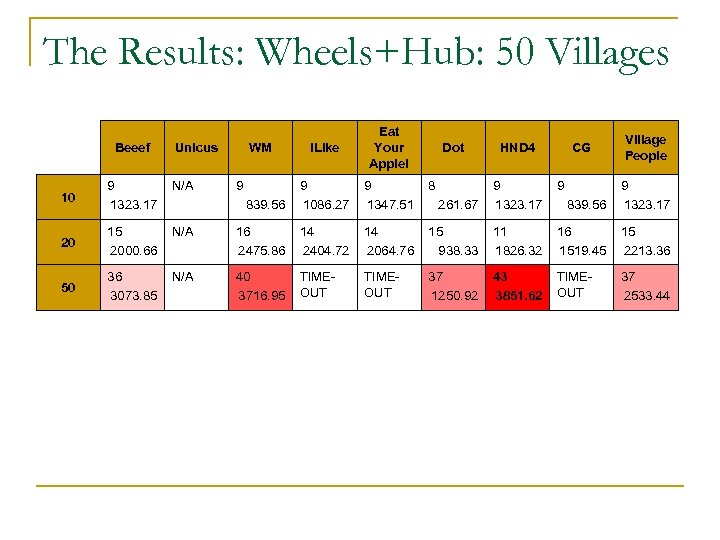The Results: Wheels+Hub: 50 Villages Beeef i. Like Eat Your Apple! 9 1086. 27 9 1347. 51 8 839. 56 Unicus WM 10 9 1323. 17 N/A 9 20 15 2000. 66 N/A 16 2475. 86 14 2404. 72 50 36 3073. 85 N/A 40 3716. 95 TIMEOUT Dot HND 4 CG Village People 9 261. 67 9 1323. 17 839. 56 9 1323. 17 14 2064. 76 15 938. 33 11 1826. 32 16 1519. 45 15 2213. 36 TIMEOUT 37 1250. 92 43 3851. 62 TIMEOUT 37 2533. 44

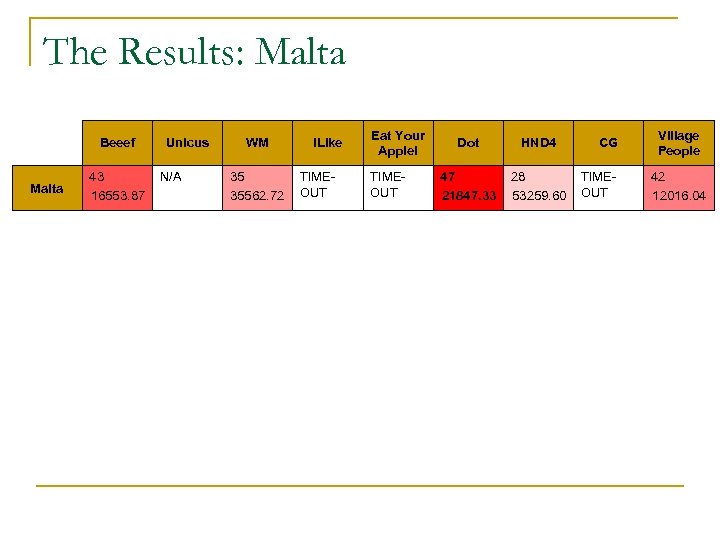The Results: Malta Beeef Malta 43 16553. 87 Unicus N/A WM 35 35562. 72 i. Like TIMEOUT Eat Your Apple! TIMEOUT Dot HND 4 47 21847. 33 28 53259. 60 CG TIMEOUT Village People 42 12016. 04

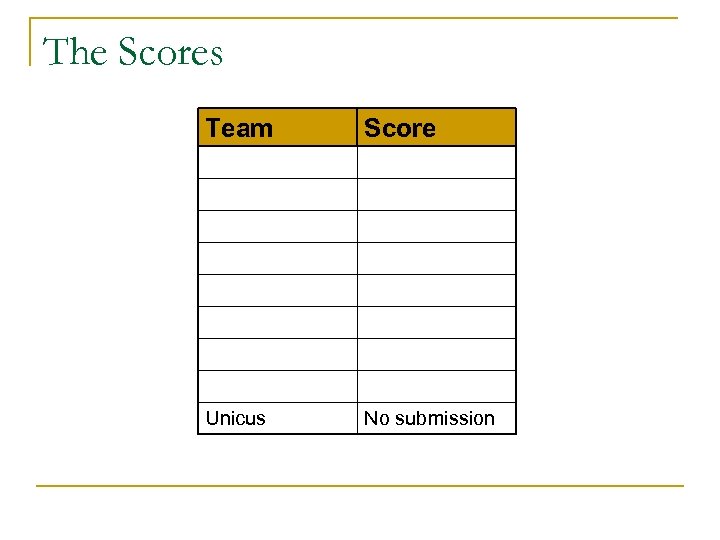The Scores Team Score Unicus No submission

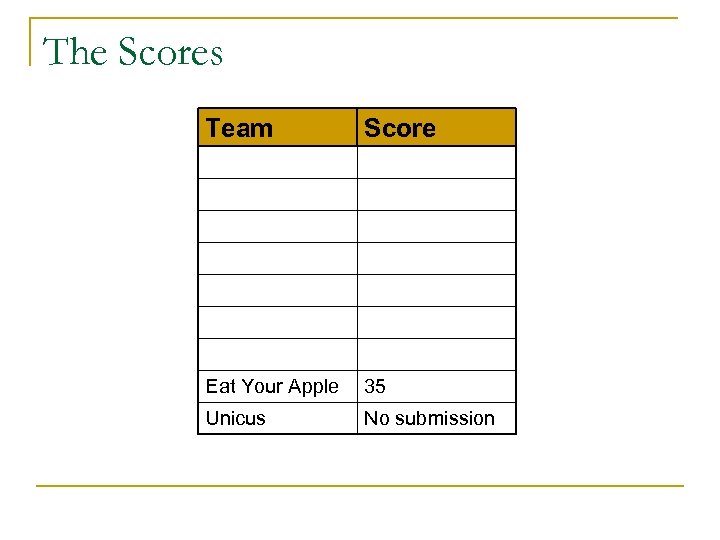The Scores Team Score Eat Your Apple 35 Unicus No submission

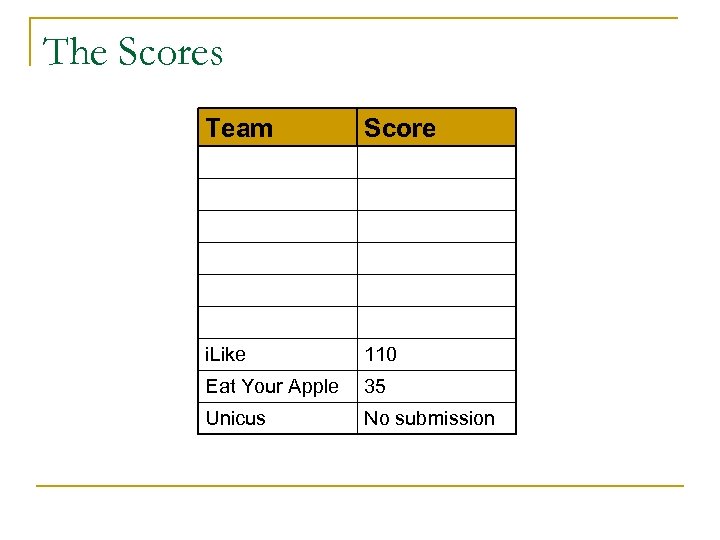The Scores Team Score i. Like 110 Eat Your Apple 35 Unicus No submission

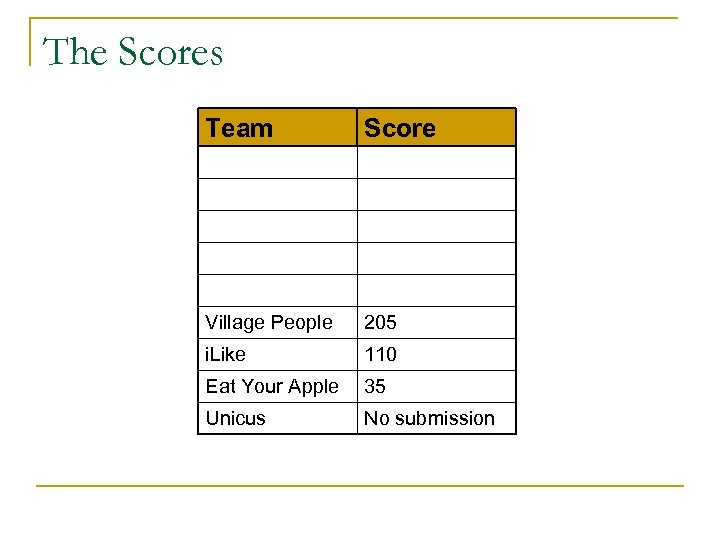The Scores Team Score Village People 205 i. Like 110 Eat Your Apple 35 Unicus No submission

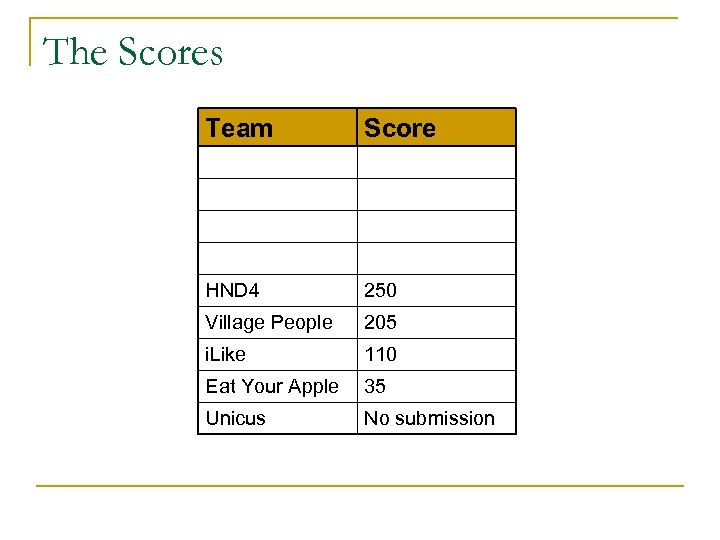The Scores Team Score HND 4 250 Village People 205 i. Like 110 Eat Your Apple 35 Unicus No submission

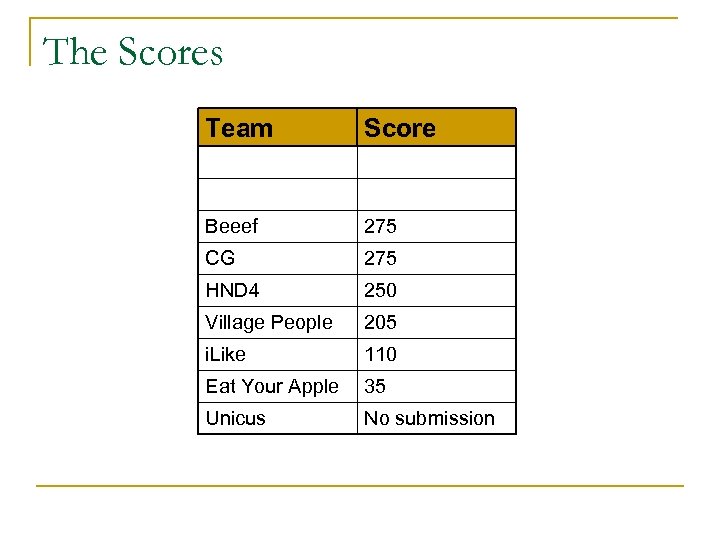The Scores Team Score Beeef 275 CG 275 HND 4 250 Village People 205 i. Like 110 Eat Your Apple 35 Unicus No submission

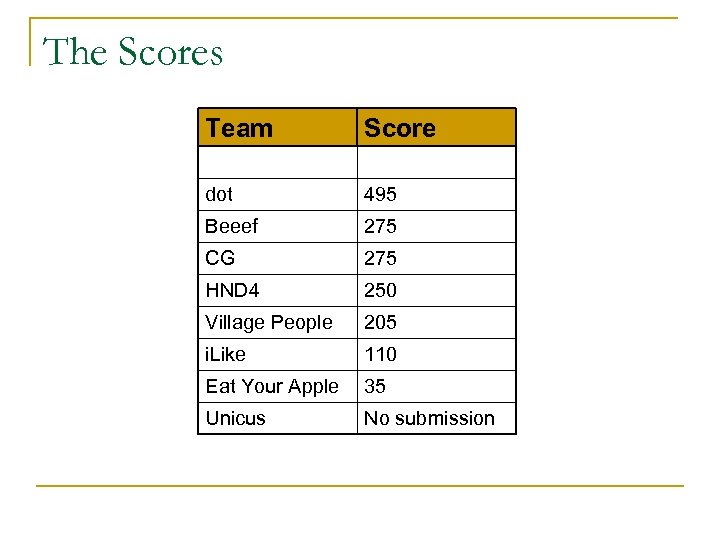The Scores Team Score dot 495 Beeef 275 CG 275 HND 4 250 Village People 205 i. Like 110 Eat Your Apple 35 Unicus No submission

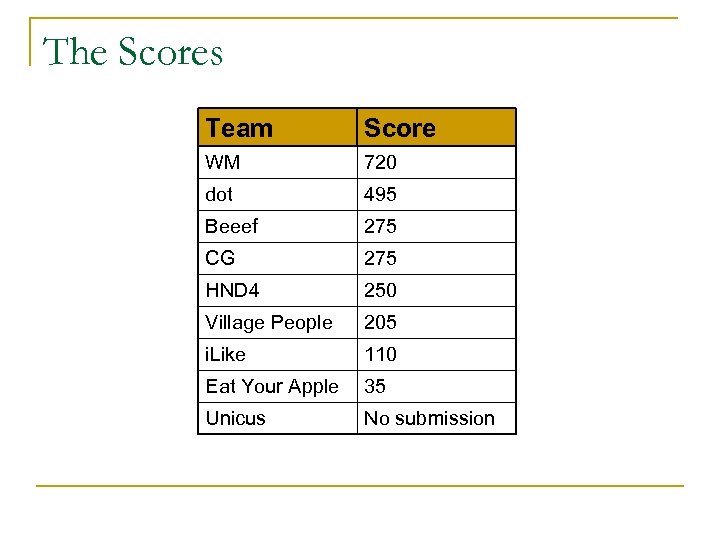The Scores Team Score WM 720 dot 495 Beeef 275 CG 275 HND 4 250 Village People 205 i. Like 110 Eat Your Apple 35 Unicus No submission

An Observation n Interesting result: q q n One team managed to elect 47 members of parliament in Malta out of 65! (PX=PL) Switching parties (not part of the contest) resulted in another layout electing 43 members for the other party. (PX=PN) In practice variance should be given more importance so as not to be accused of breach of the Constitution of Malta 61(4): q “the number obtained by dividing the total electorate in the division by the number of members to be returned to the House of Representatives from that division is as nearly equal to the electoral quota as is reasonably practicable”

Prosit tal-Programmi! n The password of the test suite was the first line of the Brikkuni song Il-Bar ta’ Taħt il. Knisja: Fil-bar ta’ taħt il-knisja jonxru ħwejjeġ tal-mistħija u smajt li bintek tgħidx kemm tħobb tintelaq hemm