Icosahedral Reconstruction Wen Jiang Icosahedral Symmetry

Icosahedral Reconstruction Wen Jiang

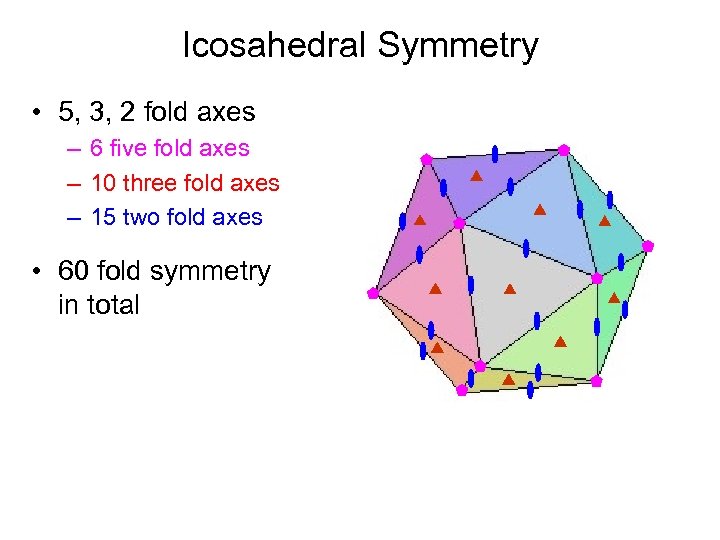Icosahedral Symmetry • 5, 3, 2 fold axes – 6 five fold axes – 10 three fold axes – 15 two fold axes • 60 fold symmetry in total

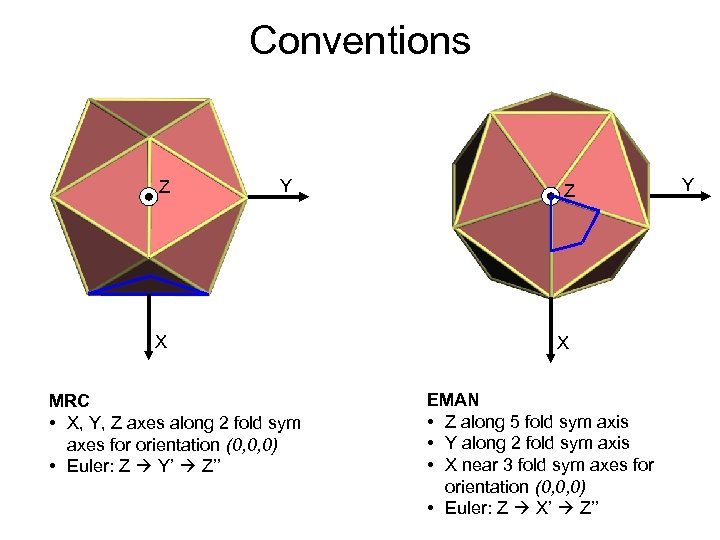Conventions Z Y X MRC • X, Y, Z axes along 2 fold sym axes for orientation (0, 0, 0) • Euler: Z Y’ Z’’ Z X EMAN • Z along 5 fold sym axis • Y along 2 fold sym axis • X near 3 fold sym axes for orientation (0, 0, 0) • Euler: Z X’ Z’’ Y

Icosahedral Particles P 22 phage 700Å Herpes Simplex Virus 1250Å pyruvate dehydrogenase 200Å

Image Processing • Preprocessing § Particle selection § CTF fitting • Image refinement § Orientation determination § 3 -D reconstruction

Particle Selection • Manual selection § boxer • Automated selection § batchboxer § ethan (for spherical particles) • By Kivioja and Bamford et al. • “Ring Filter” • Only ONE parameter (R) • Fast, 10 -15 seconds / micrograph • Tend to over-select

Ethan Example Herpes 2. 1 Å/pxiel 6662 x 8457 pixels 15 seconds in total $ time ethan. py jj 0444 -8 bit. mrc 298 600 jj 0444. box jj 0444. img Opening file jj 0444 -8 bit. mrc Width: 6662 Height: 8457 Averaging 121 pixels Filtering jj 0444 -8 bit. mrc: ***** Total number of squares is 567 Number of peaks after sector test is 163 Number of peaks after first distance check is 81 Number of peaks after discarding too small ones is 80 Refining centers 74 particles found from jj 0444 -8 bit. mrc 10. 31 s user 2. 08 s system 84% cpu 14. 578 total

CTF Fitting • Manual fitting § ctfit • Automated fitting § fitctf. py 8 unknown parameters: Z, B, A, Q, n 1, n 2, n 3, n 4 Algorithm: constrained nonlinear optimization using a sequential quadratic programming (SQP) method) subject to:

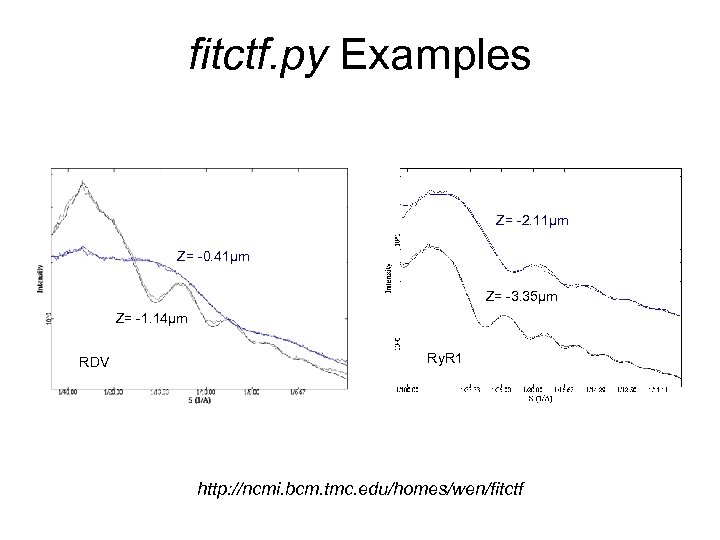fitctf. py Examples Z= -2. 11μm Z= -0. 41μm Z= -3. 35μm Z= -1. 14μm RDV Ry. R 1 http: //ncmi. bcm. tmc. edu/homes/wen/fitctf

Image Refinement • Classic method § common-lines § Fourier-Bessel reconstruction • EMAN method § projection matching § direction Fourier inversion reconstruction

Icosahedral Reconstruction Using EMAN • EMAN now supports icosahedral reconstruction • User interface is essentially the same as for other symmetries • A few points special for large virus aimed at high resolution: § projections at <1° step can use > 1 GB memory, add “projbatches=” with n>1 to refine § half 3 -D map can be used for large 3 -D map (>5003) § 3 -D reconstruction use only single CPU. can take several hours to reconstruction a large 3 -D map. working on parallel version § support mixed platform processing

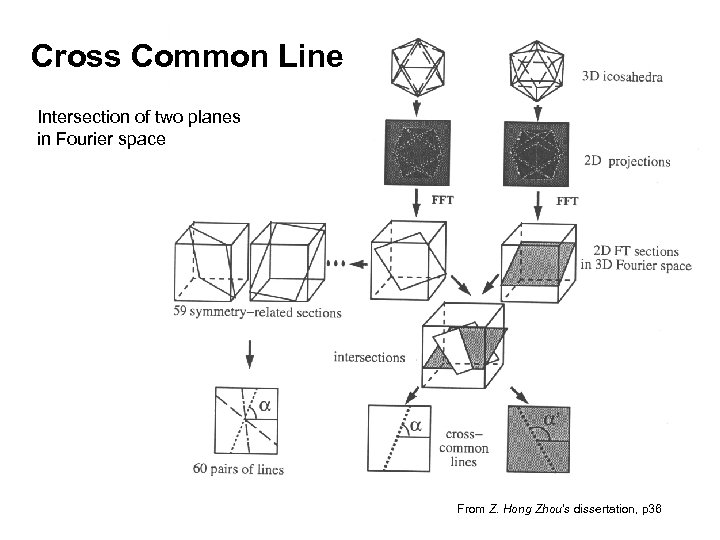Cross Common Line Intersection of two planes in Fourier space From Z. Hong Zhou’s dissertation, p 36

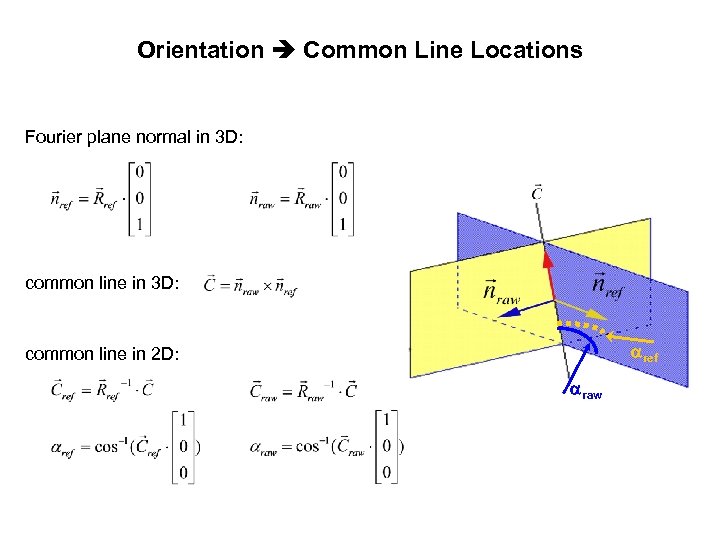Orientation Common Line Locations Fourier plane normal in 3 D: common line in 3 D: ref common line in 2 D: raw

Orientation Determination By Common Line Search search for the orientation and center parameters that minimize the mean phase differences among all the pairs of common lines

Search Strategy • Original Fortran implementation (Crowther et al) • center the particle by cross-correlation • self common line to get a starting orientation by exhaustive searching orientation in 1° step • cross common line to do local refinement of orientation and center by Gradient or Simplex.

Search Strategy • Exhaustive cross common line search • enumerate all centers and orientations in an asymmetric unit • simple but really slow • for 1 degree, 1 pixel step: 3 X 107 trials/particle

Search Strategy • A new global optimization algorithm • hybrid Monte Carlo and Simplex • global search for both orientation and center • complicated, but accurate and fast • ~4 x 103 trials/particle. • >104 times faster than exhaustive search

Is The Best Solution Correct? • Absolute score (residual) cutoff § dominant criterion § needs different cutoff values for images at different defocuses § how to pick a single number that suits all imaging conditions?

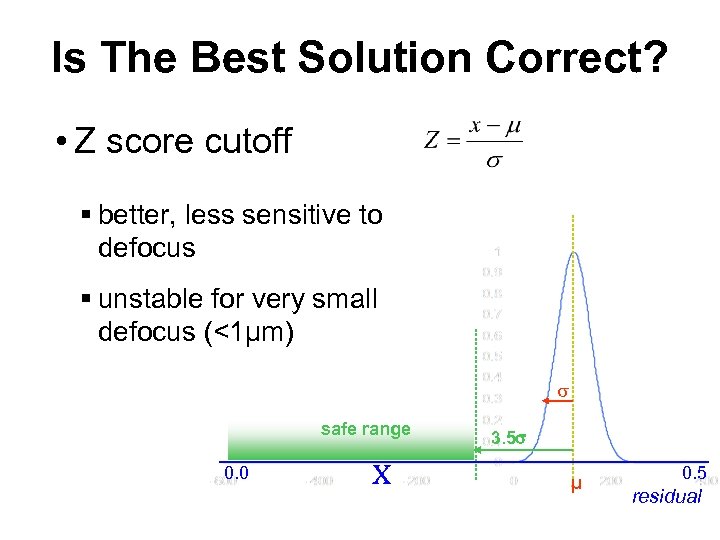Is The Best Solution Correct? • Z score cutoff § better, less sensitive to defocus § unstable for very small defocus (<1μm) safe range 0. 0 x 3. 5 μ 0. 5 residual

Is The Best Solution Correct? • Consensus cutoff § agreement among different methods (projection matching vs. common line) § agreement among multiple runs of the global common line search § more reliable than absolute value and Z-score cutoff § bias toward “safer side”

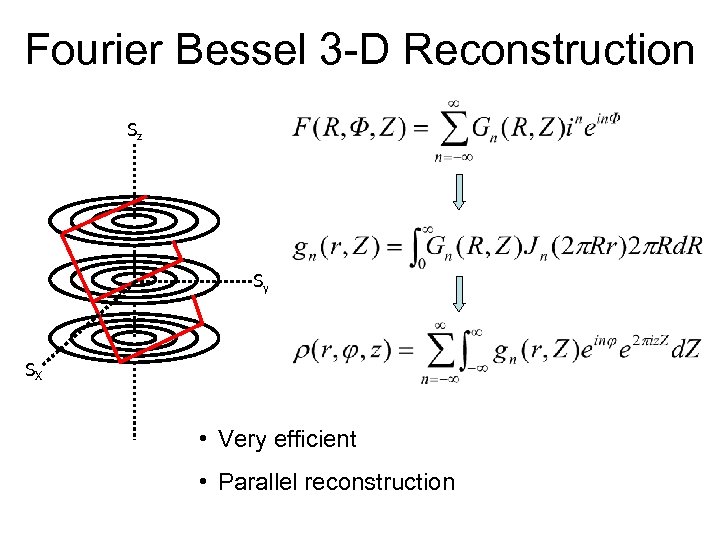Fourier Bessel 3 -D Reconstruction Sz Sy SX • Very efficient • Parallel reconstruction

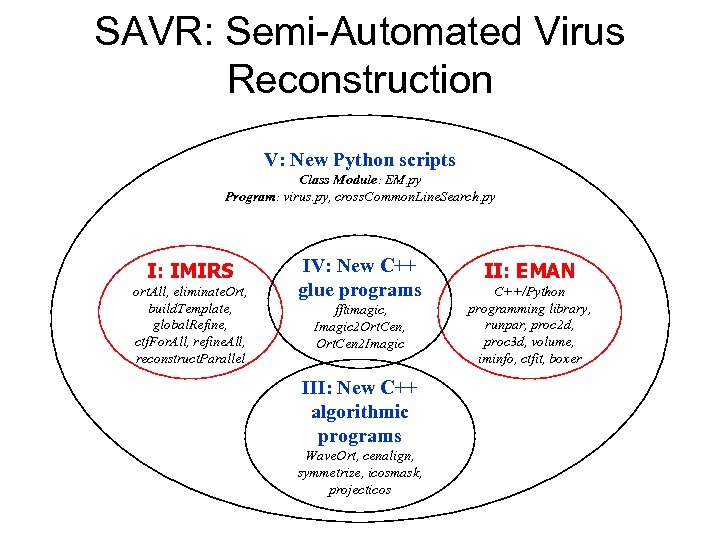SAVR: Semi-Automated Virus Reconstruction V: New Python scripts Class Module: EM. py Program: virus. py, cross. Common. Line. Search. py I: IMIRS ort. All, eliminate. Ort, build. Template, global. Refine, ctf. For. All, refine. All, reconstruct. Parallel IV: New C++ glue programs fftimagic, Imagic 2 Ort. Cen, Ort. Cen 2 Imagic III: New C++ algorithmic programs Wave. Ort, cenalign, symmetrize, icosmask, projecticos II: EMAN C++/Python programming library, runpar, proc 2 d, proc 3 d, volume, iminfo, ctfit, boxer

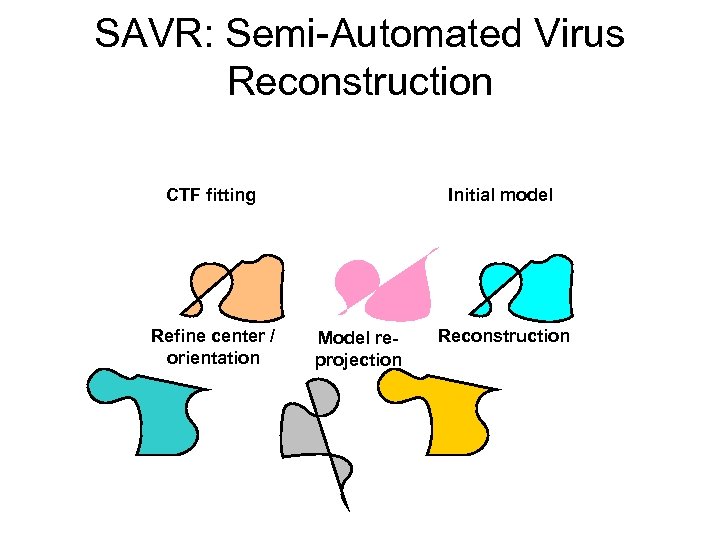SAVR: Semi-Automated Virus Reconstruction CTF fitting Refine center / orientation Initial model Model reprojection Reconstruction

Features of SAVR • Minimal user inputs to start processing and user intervention free once started • Fast crash recovery • All computation intensive steps parallelized • Cross platform compatible (shared memory and distributed memory systems) • Free from NCMI Web server (http: //ncmi. bcm. tmc. edu)

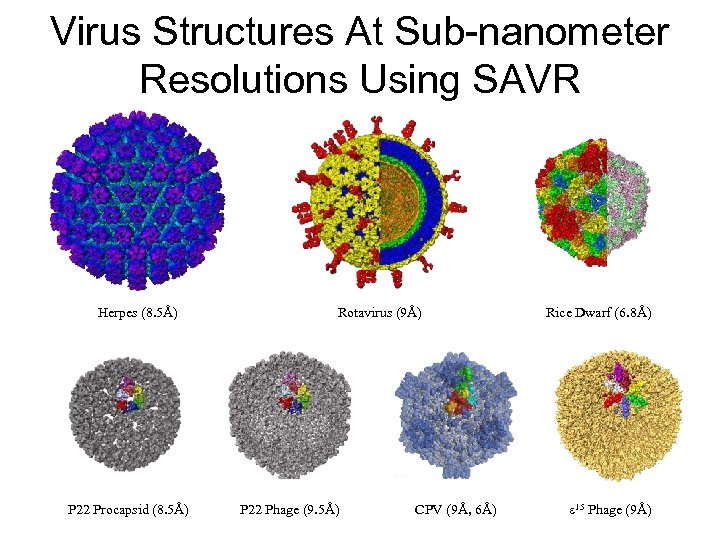Virus Structures At Sub-nanometer Resolutions Using SAVR Herpes (8. 5Å) P 22 Procapsid (8. 5Å) Rotavirus (9Å) P 22 Phage (9. 5Å) CPV (9Å, 6Å) Rice Dwarf (6. 8Å) ε 15 Phage (9Å)