ICON The next-generation global model for numerical weather

ICON The next-generation global model for numerical weather prediction and climate modeling of DWD and MPI-M Current development status and the way towards preoperational testing Günther Zängl and the ICON development team 3/19/2018 Zängl

Outline è General overview of ICON and its current development status è Selected results of idealized mountain tests and of (a very first) real-data forecast è Further planning towards preoperational testing è Summary 3/19/2018 Zängl

ICON = ICOsahedral Nonhydrostatic model è Joint development project of DWD and Max-Planck-Institute for Meteorology for the next-generation global NWP and climate modeling system è Nonhydrostatic dynamical core for triangles and hexagons as primal grid; C-grid discretization; coupling with physics parameterizations in principle completed è Two-way nesting for triangles as primal grid, capability for multiple nests per nesting level; vertical nesting, one-way nesting mode and limited-area mode are also available è Work in progress: Thorough testing (and debugging) of physics parameterizations and physics-dynamics coupling, GRIB 2 I/O, further optimization of MPI parallelization, data assimilation, ocean model on triangular grid 3/19/2018 Zängl

ICON Primary development goals è Better conservation properties (air mass, mass of trace gases and moisture, consistent transport of tracers; hexagonal core also conserves energy) è Grid nesting in order to replace both GME (global forecast model, mesh size 30 km) and COSMO-EU (regional model, mesh size 7 km) in the operational suite of DWD è Applicability on a wide range of scales in space and time ("seamless prediction"); therefore, the dynamical core was requested to be nonhydrostatic è Scalability and efficiency on massively parallel computer architectures with O(104+) cores 3/19/2018 Zängl

Project teams at DWD and MPI-M G. Zängl H. Asensio M. Baldauf K. Fröhlich M. Köhler D. Liermann F. Prill D. Reinert P. Ripodas B. Ritter A. Seifert U. Schättler Met. Bw T. Reinhardt Project leader DWD two-way nesting, parallelization, optimization, numerics external parameters NH-equation set physics parameterizations post processing, preprocessing IFS 2 ICON numerics, optimization, parallelization advection schemes test cases, power spectra physics parameterizations cloud microphysics software design physics parameterizations M. Giorgetta Project leader MPI-M physics parameterizations M. Esch software maintenance A. Gaßmann NH-equations, numerics P. Korn ocean model L. Kornblueh software design, hpc L. Linardakis parallelization, grid generators S. Lorenz ocean model C. Mosley regionalization R. Müller pre- and postprocessing T. Raddatz external parameters F. Rauser adjoint version of the SWM W. Sauf Automated testing (Buildbot) U. Schulzweida external post processing (CDO) H. Wan 3 D hydrostatic model version, physics parameterizations External: R. Johanni: MPI-Parallelization 3/19/2018 Zängl

The horizontal grid 3/19/2018 Zängl

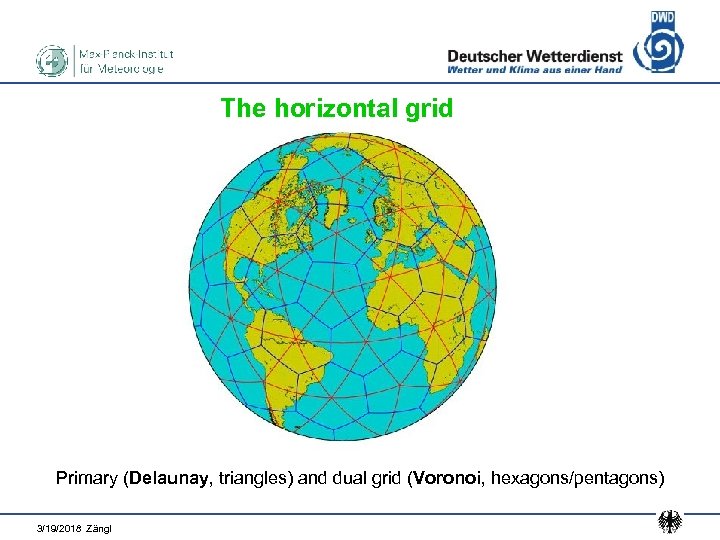
The horizontal grid Primary (Delaunay, triangles) and dual grid (Voronoi, hexagons/pentagons) 3/19/2018 Zängl

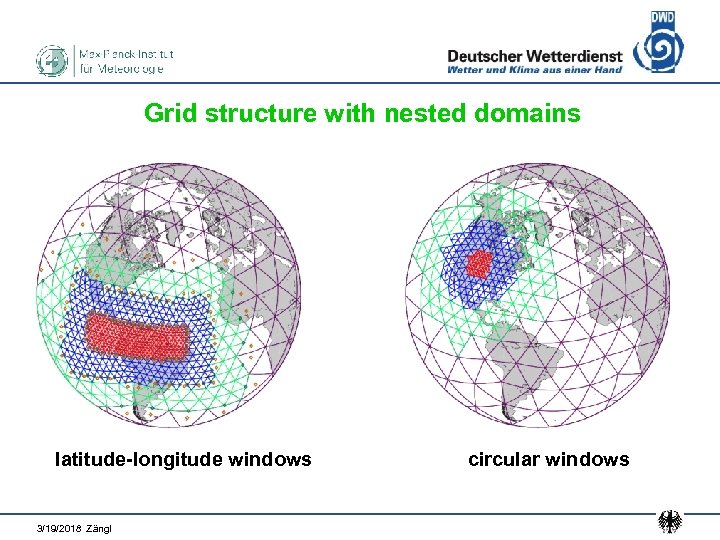
Grid structure with nested domains latitude-longitude windows 3/19/2018 Zängl circular windows

Nonhydrostatic equation system vn, w: normal/vertical velocity component : density v: Virtual potential temperature K: horizontal kinetic energy : vertical vorticity component : Exner function blue: independent prognostic variables 3/19/2018 Zängl

Numerical implementation • Two-time-level predictor-corrector time stepping scheme • 2 D Lamb transformation for nonlinear momentum advection • Flux form for continuity equation and thermodynamic equation; Miura 2 nd-order upwind scheme (centered differences) for horizontal (vertical) flux reconstruction • implicit treatment of vertically propagating sound waves, but explicit time-integration in the horizontal (at sound wave time step; not split-explicit); larger time step (default 4 x) for tracer advection / fast physics • Mass conservation and tracer mass consistency 3/19/2018 Zängl

Numerical implementation • Finite-volume tracer advection scheme (Miura) with 2 nd-order and 3 rd -order accuracy for horizontal advection; 2 nd-order MUSCL and 3 rdorder PPM for vertical advection with extension to CFL values larger than 1; monotonous and positive-definite flux limiters Special measures to improve the numerical stability over steep terrain: • Option for truly horizontal temperature diffusion over steep slopes • Option for truly horizontal discretization of the horizontal pressure gradient over steep slopes 3/19/2018 Zängl

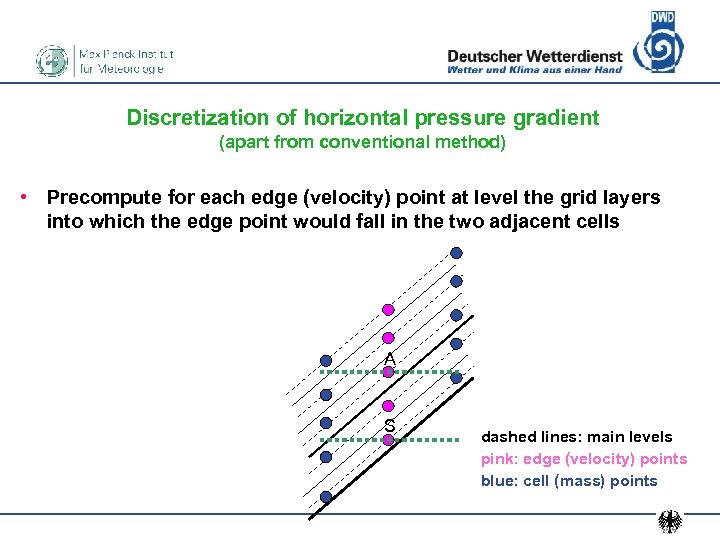
Discretization of horizontal pressure gradient (apart from conventional method) • Precompute for each edge (velocity) point at level the grid layers into which the edge point would fall in the two adjacent cells A S dashed lines: main levels pink: edge (velocity) points blue: cell (mass) points

Discretization of horizontal pressure gradient • Reconstruct the Exner function at the mass points using a quadratic Taylor expansion, starting from the point lying in the model layer closest to the edge point • Note: the quadratic term has been approximated using the hydrostatic equation to avoid computing a second derivative • Treatment at slope points where the surface is intersected:

Physics parameterizations • Cloud microphysics from COSMO-EU (hydci_pp) • New mass-conserving saturation adjustment scheme (U. Blahak/ A. Seifert) • Turbulence schemes from COSMO-model (M. Raschendorfer) and ECHAM • Tiedtke-Bechtold convection scheme (from ECMWF) • COSMO cloud cover scheme; new scheme under development by M. Köhler • Ritter-Geleyn and RRTM radiation schemes • TERRA surface scheme 3/19/2018 Zängl

Idealized steep-mountain test • Isolated circular Gaussian mountain, e-folding width 2000 m, various mountain heights (see subsequent slides) • Isothermal atmosphere at rest or with u 0 = 20 m/s • Horizontal mesh size 300 m • 50 vertical levels, top at 40 km, gravity-wave damping layer starts at 27. 5 km • dry dynamical core with turbulence scheme for vertical mixing • Results are shown after 6 h of integration time

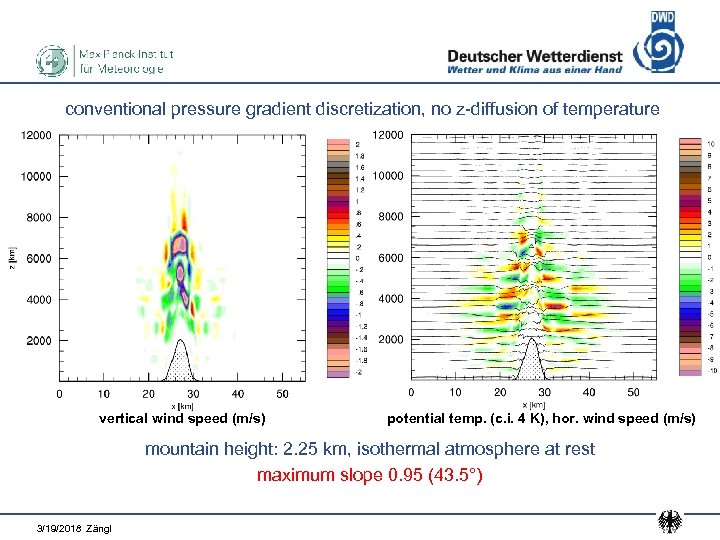
conventional pressure gradient discretization, no z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 2. 25 km, isothermal atmosphere at rest maximum slope 0. 95 (43. 5°) 3/19/2018 Zängl

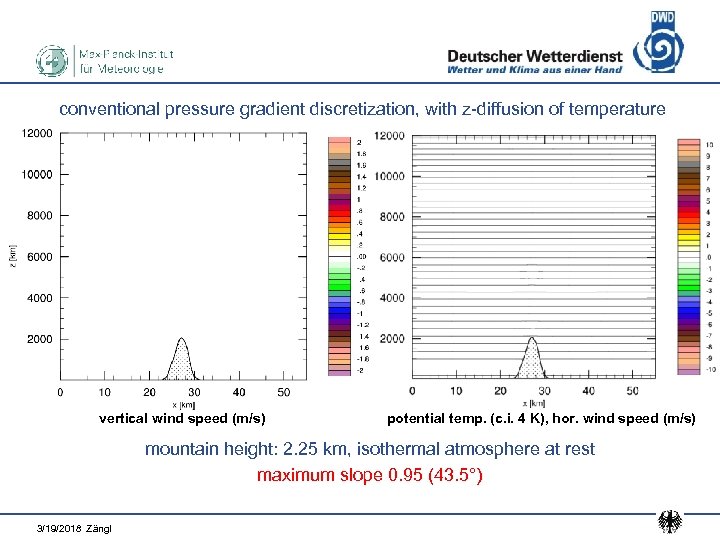
conventional pressure gradient discretization, with z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 2. 25 km, isothermal atmosphere at rest maximum slope 0. 95 (43. 5°) 3/19/2018 Zängl

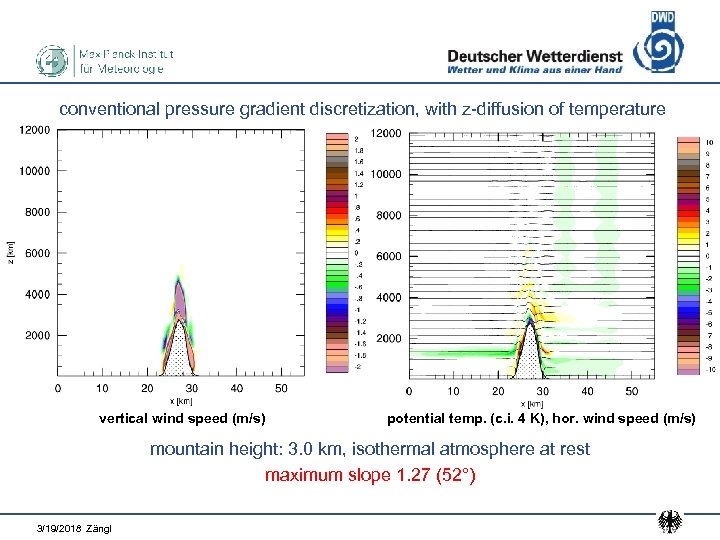
conventional pressure gradient discretization, with z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 3. 0 km, isothermal atmosphere at rest maximum slope 1. 27 (52°) 3/19/2018 Zängl

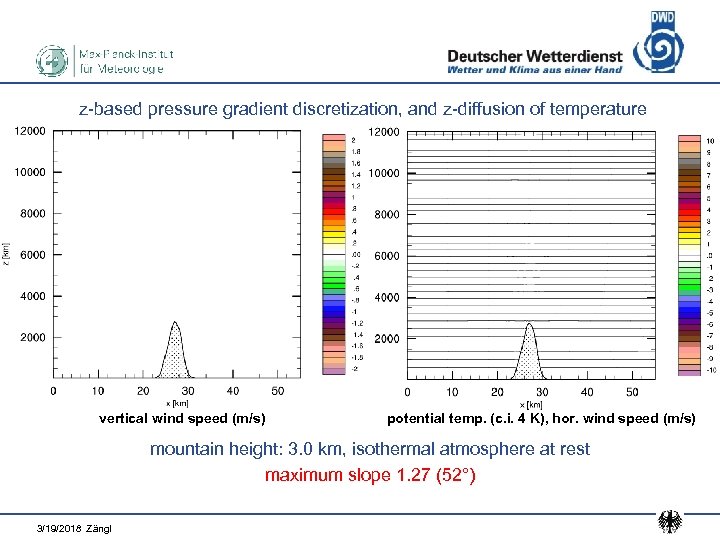
z-based pressure gradient discretization, and z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 3. 0 km, isothermal atmosphere at rest maximum slope 1. 27 (52°) 3/19/2018 Zängl

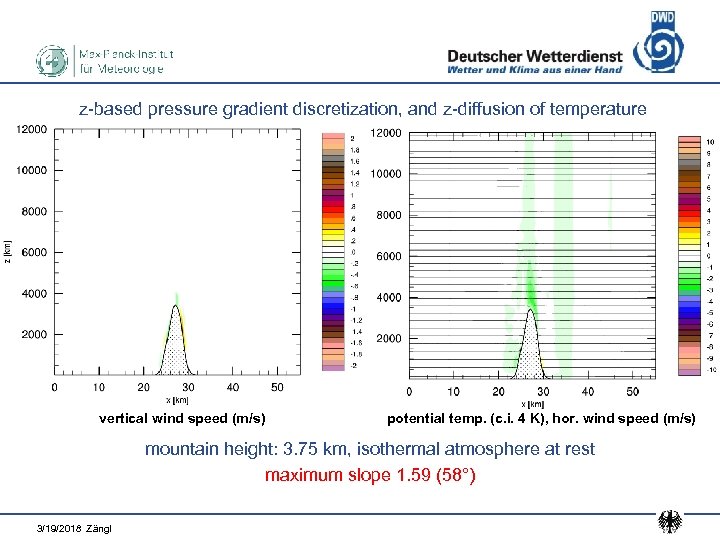
z-based pressure gradient discretization, and z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 3. 75 km, isothermal atmosphere at rest maximum slope 1. 59 (58°) 3/19/2018 Zängl

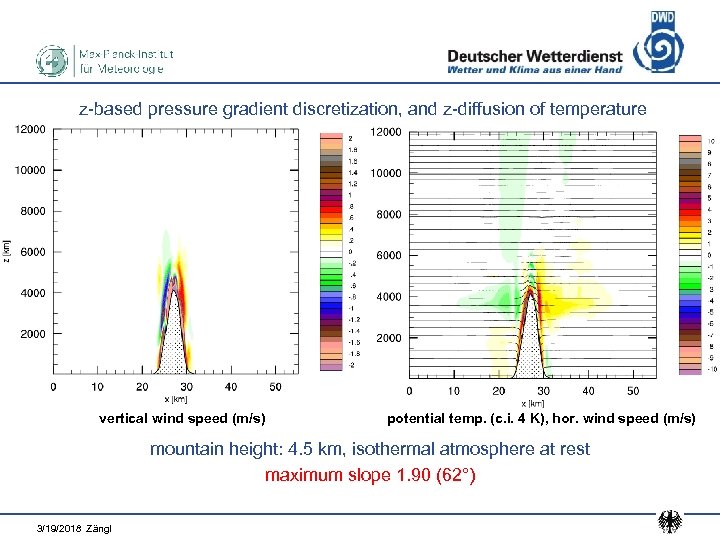
z-based pressure gradient discretization, and z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 4. 5 km, isothermal atmosphere at rest maximum slope 1. 90 (62°) 3/19/2018 Zängl

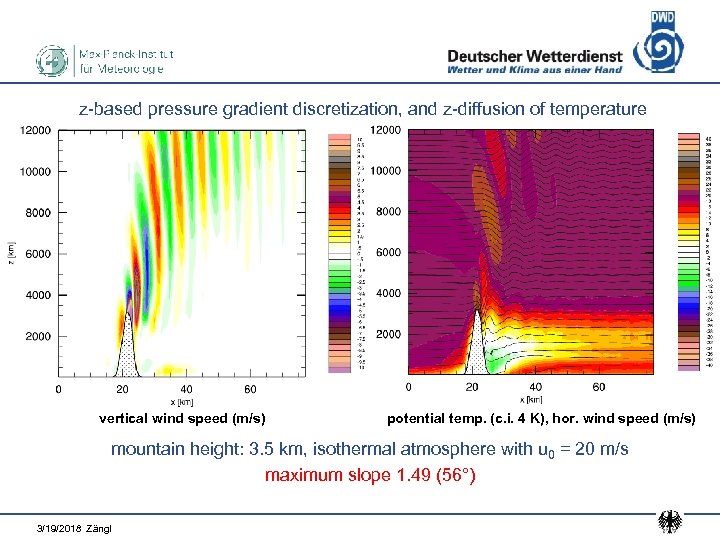
z-based pressure gradient discretization, and z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 3. 5 km, isothermal atmosphere with u 0 = 20 m/s maximum slope 1. 49 (56°) 3/19/2018 Zängl

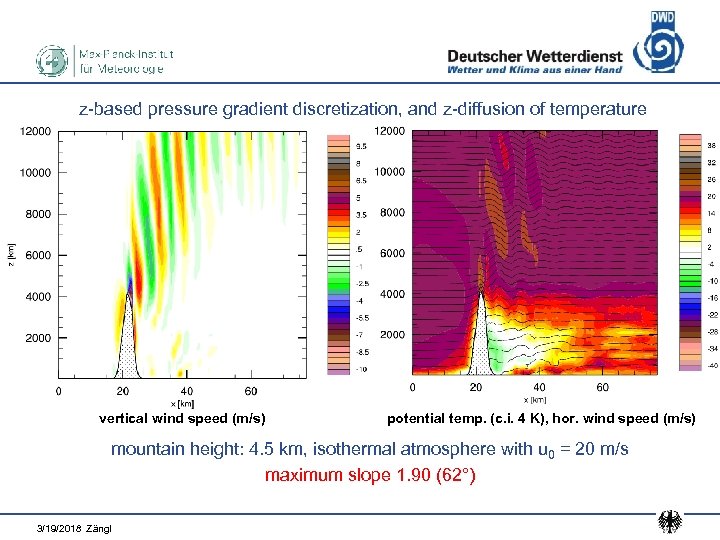
z-based pressure gradient discretization, and z-diffusion of temperature vertical wind speed (m/s) potential temp. (c. i. 4 K), hor. wind speed (m/s) mountain height: 4. 5 km, isothermal atmosphere with u 0 = 20 m/s maximum slope 1. 90 (62°) 3/19/2018 Zängl

Real-data test • Global mesh size 40 km, refinement to 20 km over Europe • Model top at 45 km, 60 levels (another expt. : 67. 5 km / 90 levs) • Time step in global domain: 60 s / 240 s • Initialization with interpolated IFS analysis data for 01. 2011 • Total integration time: 20 days • Results shown on subsequent slides: 3 -day forecast in comparison with corresponding analysis data

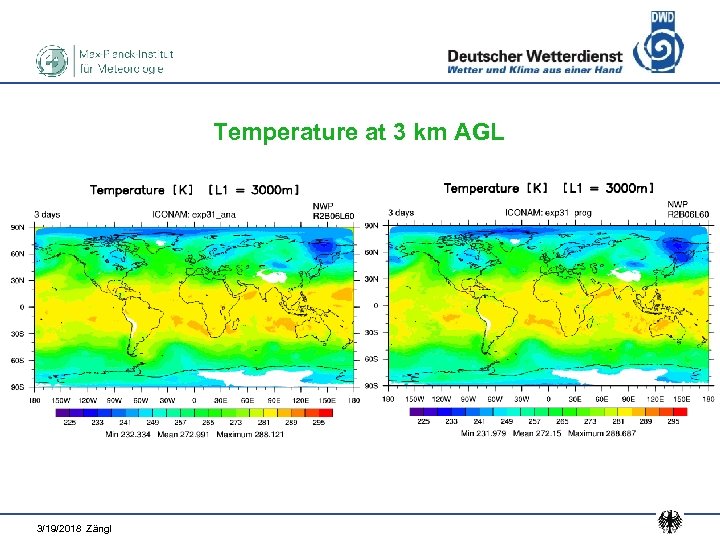
Temperature at 3 km AGL 3/19/2018 Zängl

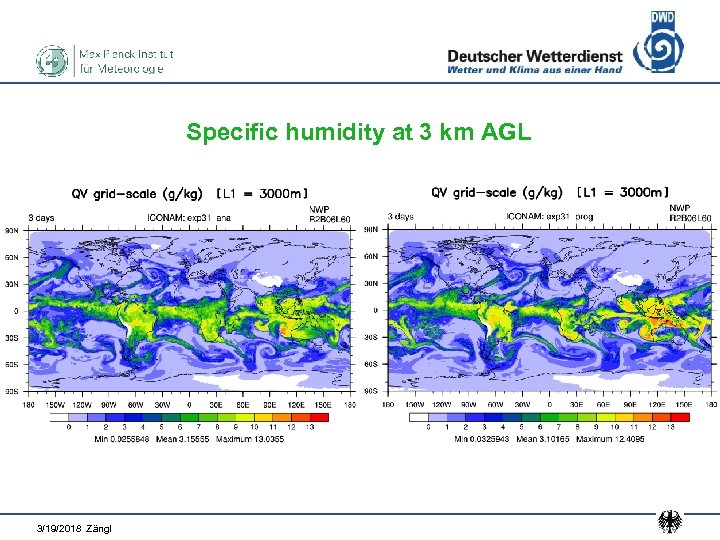
Specific humidity at 3 km AGL 3/19/2018 Zängl

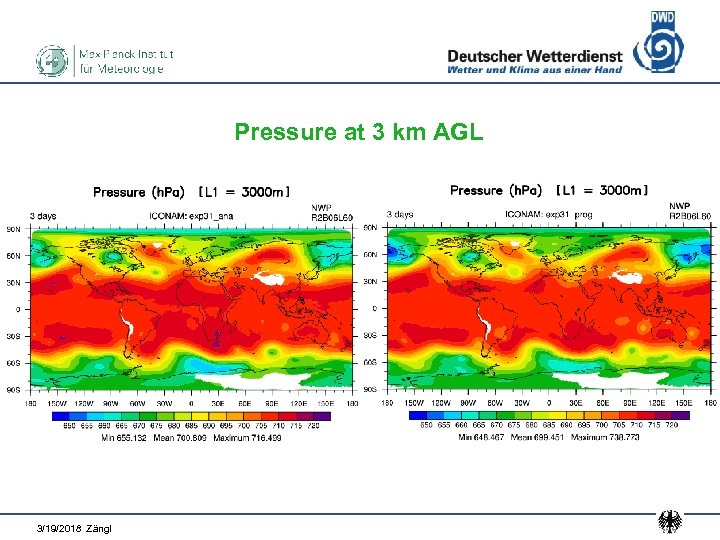
Pressure at 3 km AGL 3/19/2018 Zängl

Further steps towards preoperational testing • Thorough investigation of still exisiting numerical instabilities; bug fixes or improvement of algorithms • Test suites for ICON and GME with interpolated IFS analysis data; systematic tuning of physics parameterizations and their mutual interaction (maybe also physics-dynamics coupling) • Work on GRIB 2 I/O, interpolation to lat-lon grid and pressure/ height levels, meteogram output, … • Data assimilation 3/19/2018 Zängl

Conclusions and further remarks • We are on a good way, but there is still a lot to do… • Efficiency and scalability: significantly better than for GME; roughly comparable to the COSMO model • Time planning: start with preoperational testing late 2011 / early 2012; operational use (hopefully) by mid-2013 3/19/2018 Zängl