caed2f1c2833bfd9a8ab5c51ec024866.ppt
- Количество слайдов: 19

İÇİN YENİ BİR SERİ A NEW SERIE FOR BİRİNCİ BÖLÜM e-mail Yorumunuz > SECOND PART taneryonder@yahoo. com < > < contacts to e-mail

TANER YÖNDER SERİLERİ İSPATI İLK DEFA PİSAGOR BAĞINTISIYLA YAPILAN SAYISININ 4 AYRI YOLDAN BULUNMASI 1 - KENAR SAYISI OLMAK ÜZERE, BİR DAİRE İÇİNDE KİRİŞ OLUŞTURAN BİR KENAR UZUNLUĞUNUN 4, 8, 16, 32. . . n GEN'LER OLUŞTURACAK ŞEKİLDE ÇOĞALTILIP BULUNAN UZUNLUKLARIN İLE ÇARPIMININ ÇAPA BÖLÜNEREK 'NİN BULUNMASI. BİRİM 2 r = 1 2 - 3 x KENAR SAYISI OLMAK ÜZERE BİR DAİRE İÇİNE ÇİZİLEN EŞKENAR ÜÇGENİN DAİRE İÇİNDE KİRİŞ OLUŞTURAN HER KENARININ 3, 6, 12, 24. . . n GEN'LER OLUŞTURACAK ŞEKİLDE ÇOĞALTILIP BULUNAN KENAR UZUNLUKLARIN 3 x İLE ÇARPIMININ , ÇAPA BÖLÜNEREK SAYISININ BULUNMASI. BİRİM 2 r = 1 3 - BİRİM DAİRE İÇİNE ÇİZİLEN KARE'NİN ALANINDAN YARARLANILARAK , BİRİM DAİRENİN ALANININ HESAPLANARAK r 2 'YE BÖLÜNEREK SAYISININ BULUNMASI. BİRİM 2 r = 1 ~ < >

TANER YÖNDER SERİLERİ 4 - BİRİM DAİRE İÇİNE ÇİZİLEN EŞKENAR ÜÇGENİN ALANINDAN YARARLANILARAK, BİRİM DAİRENİN ALANININ HESAPLANARAK r 2 'YE BOLUNEREK SAYISININ BULUNMASI. BİRİM 2 r =1 5 - TÜM BU İŞLEMLERDEN SONRA SAYISININ BULUNABİLMESİ İÇİN GENEL İFADE YAZMAK İSTERSEK, FAVORİ SERİMİZDE. . . EŞİTLİĞİ ORTAYA ÇIKAR - HATA NİSYAN MÜSTESNADIR. NOT: YUKARIDAKİ SERİLERDE vs. ‘ İLE GÖSTERİLEN SAYILAR İŞLEM BELİRLİ BİR NOKTADA KESİLMEK İSTENDİĞİNDE İFADENİN SON OLARAK ÇARPILACAĞI KATSAYILARDIR. İŞLEM KESİLDİĞİ NOKTADAN ÖNCE SERİLERİN ALTINDA VERİLEN KATSAYILAR DİKKATE ALINMAMALIDIR < >

TANER YÖNDER SERİLERİ LÜTFEN AŞAĞIDAKİ HAREKETLİ KIRMIZI ANİMASYONU TAKİP EDİNİZ Bu seriye devam ettiğiniz takdirde sayısına ulaşacaksınız. KAYNAK GÖSTERİLEK YAZILI MAKALE VEYA İNTERNET'TE LİNK AÇILARAK YAYIMLANABİLİR. FİKİR VE SANAT ESERLERİNİ KORUMA KANUNU KAPSAMINDADIR. . TASDİK TARİHİ 03. ŞUBAT. 1997 NO: 4085 2. NOTER MANİSA / TÜRKİYE < >

π SAYISININ PİSAGOR TEOREMİYLE İSPATI. Çapı 2 r =X=1 olan dairenin içine çizilen 4 , 8, 16 , 32 gen in birer kenarlarını sırasıyla, X 1, X 2, X 3, X 4 diye tanımlarsak, Pisagor bağıntısından faydalanarak, kenar uzunluklarının, X 1=0. 707106781. . n, X 2=0. 382643439. . n, X 3=0. 0195090314. . n, X 4=0. 098017136. . n değerlerinde olduğunu buluruz, tabii bu kenarların birbirlerine aralarında bir oran olması kaçınılmazdır ama bu oran, acaba nasıl bir orandır. X / X 1 den başlayarak bulunan kenar uzunluklarını birbirine bölme işlemleri sırasıyla. . X / X 1 / X 2 / X 3 / X 4. . n şeklinde yapılırsa. SIRA İLK KENAR SONRAKİ KENAR BULUNAN ORAN X / X 1= 2 r = 1 / 0. 707106781. . . n = 1. 414213562. . . n X 1/X 2= 0. 707106781. . . n / 0. 382683439. . . n = 1. 847759064. . . n X 2/X 3= 0. 382683439. . . n / 0. 195090314. . . n = 1. 961570562. . . n X 3/X 4= 0. 195090314. . . n / 0. 098017136. . . n = 1. 990369453. . . n Oranlarında olduğunu göreceğiz. Bu kere X / X 1. . . n olarak önerilen serimizdeki ilk işlemden başlayarak, ( X=2 r=1 ) . . . n İşlemlerİ sırasıyla yapılırsa ve önerilen seri doğru ise, bir önceki işlemde pisagor bağıntısıyla hesaplanan 4 -8 -16 -32 genlerin kenar uzunluklarını aynen bulmamız gerekmektedir. >>> < >

π SAYISININ PİSAGOR TEOREMİYLE İSPATI ONDALIK DEĞER SONRAKİ KENAR / 1. 414213562. . . n = 0. 707106781. . . n = 1. 847750064. . . n => 0. 707106781. . . n / 1. 847750064. . . n = 0. 382683439. . . n = 1. 961570562. . . n => 0. 382683439. . . n / 1. 961570562. . . n = 0. 195090314. . . n = 1. 990369453. . . n => 0. 195090314. . . n / SERİLER 1. 990369453. . . n = 0. 098017136. . . n ONDALIK DEĞER İLK KENAR = 1. 414213562. . . n => 2 r = 1 Sonuç olarak, daha önce Pisagor bağıntısı ile bulunan kenar uzunluklarını, önerilen ve uygulanan yeni seri ile bulabildiğimizden, ispat tartışmasız doğrudur. Bu seriyi kullanarak bulunan 2 n+1 kenarlı çokgenin, kenar uzunlukları toplamını olan çemberin çevresini, çapa bölersek sayısına giderek yakınlaşacağımızı aşağıda ~ görebiliriz. ÖRNEK => 0. 707106781. . . n X 4 GEN = 2. 828427124. . . n 0. 382683439. . . n 0. 195090314. . . n 0. 098017136. . . n X X X 8 GEN 16 GEN 32 GEN = 3. 061467512. . . n = 3. 121225024. . . n = 3. 136548352. . . n < >

. π SAYISININ KISA BİR TARİHİ 1. Ondalıkları sonsuz olan sayısı günümüze kadar çok değişik teoremlerle bulunmuştur, hatta Japon Yasuma KANADA, 206. 158. 430. 000 ondalığa kadar hesaplayarak bir dünya rekorunuda kırmıştır, ancak sayısını ispatlamak ve anlamak ayrı bir konu olduğundan, trigonometri , logaritma , integral , türev , limit vs. bilinmesi şarttır, mevcut ispatları 7 sınıf öğrencilerinin anlamasıda mümkün değildir. 2. Oysa, Şimdi Önerilen yeni seri ve formülleri, eğitim seviyesi c 2=a 2 + b 2 bağıntısını ( Pisagor teoremini ) ve 4 işlemi bilen 7 sınıf öğrencileri dahi sayısının nasıl bulunduğunu ve de ispatını anlayabilirler. Araştırmalarımıza göre bu kadar basit anlatıma veya ispata literatürde rastlanmamıştır. 3. Klasik yöntemle, Yunanlı Arşimed, 'nin 3 ondalık basamağını; 1479'da Uluğ Bey' in gök bilimcisi, Al-Kaşi 16 ondalık basamağını; 1579'da Fransız F. Viete 9 ondalık basamağını bulmuş, ayrıca 2 / 'ye giden sonsuz bir seri yazmıştır, 1593'te Hollandalı Adrian Van Roomen 15 ondalığı; 1610'da Ludolph Van Coulen 35 ondalık basamağı bulmak için hayatının büyük bir kısmını harcamıştır. 4. Burada kullandığım yöntemde klasik, yani dairenin kenar uzunluğunun çapa bölünmesine dayanmaktadır ama farklı olan, çokgenlerin kenar uzunluklarını bulmak için uzun süre gerekmemektedir. Sadece ispattan tatmin olmak için, pisagor teoreminden faydalanarak bulunan 4 -8 -16 -32 genlerin kenar uzunluklarını, sırasıyla birbirine bölerek ortaya çıkan oranların favori yeni serimizle bulunan oranlarla eşit olduğunu göstermektedir, bu eşitlik 2 n+1 gen'e kadar devam edeceği süphe götürmediğinden matematik çevrelerince, bu serinin doğruluğu ve anlaşılma düzeyinin ORTA EĞİTİM seviyesinde olmasından dolayıda kabul göreceği muhakkaktır. < >

TANER YÖNDER’İN DİĞER ÇALIŞMALARI AŞAĞIDA İFADE EDİLMEYE ÇALIŞILAN SERİLER, TARAFIMDAN YAPILMIŞTIR, BİLİNEN VE KABUL EDİLEN İSPATI YAPILMIŞ 3. 14159265358. . . n SAYISIYLA EŞ OLUP, BİRE BİR DOĞRUDUR, FANTAZİ BİR ÇALIŞMADIR, LİTERATÜRDE RASTLANMAMIŞTIR. A 8 8 8 = ( - ) + ( ------------- ) + ( -------- ) +. . . n 3 (1 x 32)+3 [(1+2)x 32]+3 [(1+2+3)x 32]+3 B 8 8 = --------- + ----- +. . . n 2 2 (2 x 1)-1 (2 x 3)-1 (2 x 5)-1 (2 x 7)-1 (2 x 9)-1 (2 x 11)-1 C 8 8 8 = ------ + -------- + ----- +. . . n 2 2 (2)-1 (6)-1 (10)-1 (14)-1 (18)-1 (22)-1 YUKARIDAKİ İŞLEMLERİN SONUCU, AŞAĞIDAKİ SAYISAL SERİYE GİTMEKTEDİR D 8 8 8 = ----- + ----- + ------ +. . . n 3 35 99 195 323 483 675 899 1155 < >

ÖZ GEÇMİŞ 1947' DE MANİSA'DA DOĞDUM, 8'NCİ SINIFA KADAR ÖĞRENİM GÖRDÜM. LASTİK BAYİLİĞİ YAPMAKTAYIM, SAYILARA KARŞI OLAN İLGİMDEN DOLAYI AMATÖR BİR MATEMATİKÇİ OLDUM. x 10 : 9 VE BUNUN KARESİ 9. 876543210. . n İLE KARŞILAŞTIM, BU SAYININ DOĞAL GÜZELLİĞİNDEN ETKİLENDİM. x 10 : 9 = 3. 14269680529. . n 'İN SAYISI OLABİLECEĞİNİ SANDIM. ÜST DÜZEYDE MATEMATİK BİLMEDİĞİMDEN HATAMI HEMEN GÖREMEDİM AMA BİRKAÇ YIL SONRA İRRASYONEL VE TRANSANDANTAL ( ÜSTÜN- AŞKIN ) SAYILAR KAVRAMINI ÖĞRENİNCE BU SAYININ NEDEN SAYISI OLAMIYACAĞINI ANLADIM. SAYISININ BİLİNEN AÇIKLANMALARININ YANINDA, TRİGONOMETRİ GEREKTİRMEYECEK ÇOK DAHA BASİT BİR İZAHININ OLABİLECEĞİNE İNANIYORDUM. ÇALIŞMALARIM SONUNDA 2000 YILDIR GÖZDEN KAÇAN VE İSPAT BÖLÜMÜNDE ANLATILAN ÇOKGENLERİN KENARLARI ARASINDAKİ ORANLARI FARKETTİM. SONUÇLARI = 3. 14159265358. . . n OLAN ÖNCEKİ TÜM ÖNERME VE İSPATLARIN HEPSİ DOĞRUDUR, BASİT BİR GÖSTERMEYLE MATEMATİK DÜNYASINA KAZANDIRDIĞIM BU TEOREM GİBİ KOLAY ANLAŞILAN BİR YOL VARKEN, GEÇMİŞTEN BU GÜNE KADAR MATEMATİKÇİLERİN ONLARCA ZOR YOLDAN, HALA SAYISINI BULMA VE İSPATLAMA ÇABALARINI HAYRETLE İZLEMEKTEYİM, ÖNERDİĞİM YENİ FAVORİ TEOREMİN TÜRKİYEDE VE DÜNYADA 8 YILLIK ÖĞRETİMİN SON DÖNEMİNDE DERSLERE KONMASI İÇİN MİLLİ EĞİTİM BAKANLIĞININ YETERLİ İLGİYİ GÖSTERMESİNİ ARZU ETMEKTEYİM. TANER YÖNDER KENAN EVREN SANAYİ SİTESİ 1299 ADA NO: 39 MANİSA / TÜRKİYE TEL : 0 ( 236 ) 233 33 33 < >

ORDER FIRST EDGE NEXT EDGE ONAY FOUND RATIO Matematik bölümümüz tarafından değerlendirilmiş ve web sitemizde yayımlanması uygun bulunmuştur. Prof. Dr. Necdet BİLDİK Manisa Celal Bayar Üniversitesi Matematik Bölüm Başkanı Telefon : ( 0 236 ) 201 32 03 MANİSA e-mail : necdet. bildik@bayar. edu. tr < >

SERIES TANER YÖNDER 4 DIFFERENT WAYS OF CALCULATING WHICH'S PROOF IS BASED ON PYTHAGORAS THEOREM 1 - BEING THE NUMBER OF EDGES, TO CALCULATE FROM STARTING WITH A SQUARE INSCRIBED IN A CIRCLE AND CONTINUING BY FORMING 3, 6, 12, 24. . . n GONS AND DIVING THE SUM OF THE EDGES OF THE LAST POLYGON, BY DIAMETER (2 r = 1) 2 - 3 x BEING THE NUMBER OF EDGES, TO CALCULATE FROM STARTING WITH A EQUILATERAL TRIANGLE INSCRIBED IN A CIRCLE AND CONTINUING BY FORMING 3, 6, 12, . . . n GONS AND DIVING THE SUM OF THE EDGES OF THE LAST POLYGON, BY DIAMETER (2 r = 1) 3 -TO FIND USING THE AREA OF A SQUARE INSCRIBED IN A CIRCLE AND DIVIDING IT BY r 2 ( 2 r = 1 ) < >

SERIES TANER YÖNDER 4 -TO FIND USING AREA OF AN EQUILATERAL TRIANGLE INSCRIBED IN A CIRCLE BY CALCULATING THE AREA IF THE CIRCLE AND DIVING IT BY r 2. (2 r = 1) 5 -AFTER ALL THESE CALCULATIONS, IF WE WISH TO WRITE A GENERAL FORMULA FOR WE FIND THE FOLLOWING EQUALITY. IF THERE ANY SYNTATIC ERRORS, PLEASE DO REPORT. NOTE : IN THE ABOVE FORMULAS, BY , WE MEAN THAT IF THE OPERATION IS TO BE CUT AT A CERTAIN STEP, THE RESULT WILL BE MULTIPLIED WITH THAT COEFFICIENT ( THE NUMBER OF EDGES OF THE LAST POLYGON ) AND THE OTHER PREVIOUS COEFFICIENTS ARE TO BE DISCARDED < >

SERIES TANER YÖNDER PLEASE FOLLOW THE RED ANIMATION If you continue you will reach THE ABOVE FORMULAS ARE ALL MY CREATIONS AND COMPLETE OR PARTIAL REPRODUCTION, WITH PERMISSION OF THE AUTHOR IS FREE. THIS FORMULAS CAN USE IN SCIENTIFIC EDUCATIONS WITHOUT PERMISSION OF AUTHOR. THIS WORK IS PATENTED ( DATE 03/02/1997 NR. 4085 MANi. SA 2 Nd PATENT OFFICE-TURKEY ) < >

ORDER π FIRST EDGE NEXT EDGE FOUND RATIO PROOF OF THE SERIES FOR USING PYTHAGORAS' THEOREM. Let X 1, X 2, X 3, X 4 be the lengths of edges of a 4, 8, 16, 32 -gon, respectively, which are inscribed in a circle of 2 r =X=1 diameter. Then using Pythagoras' theorem we find the values X 1=0. 707106781. . n, X 2=0. 382643439. . n, X 3=0. 0195090314. . n, X 4=0. 098017136. . n of course, there sould be ratio between these lengths of edges but what kind of ratio can this be? starting from X/X 1, if we divide succesively the lengths of the edges in the following manner, X / X 1 / X 2 / X 3 / X 4, we get the ratios. SERIES FIRST EDGE NEXT EDGE DECIMAL VALUE X / X 1= 2 r = 1 / 0. 707106781. . . n = 1. 414213562. . . n X 1/X 2= 0. 707106781. . . n / 0. 382683439. . . n = 1. 847759064. . . n X 2/X 3= 0. 382683439. . . n / 0. 195090314. . . n = 1. 961570562. . . n X 3/X 4= 0. 195090314. . . n / 0. 098017136. . . n = 1. 990369453. . . n This time, if we start by diving X / X 1. . . n with the first step suggested in the new series and continuing with ( X=2 r=1 ) . . . n • and if the suggested series if correct, then we should obtain the same lengths of edges that we computed by Pythagoras theorem. >>> < >
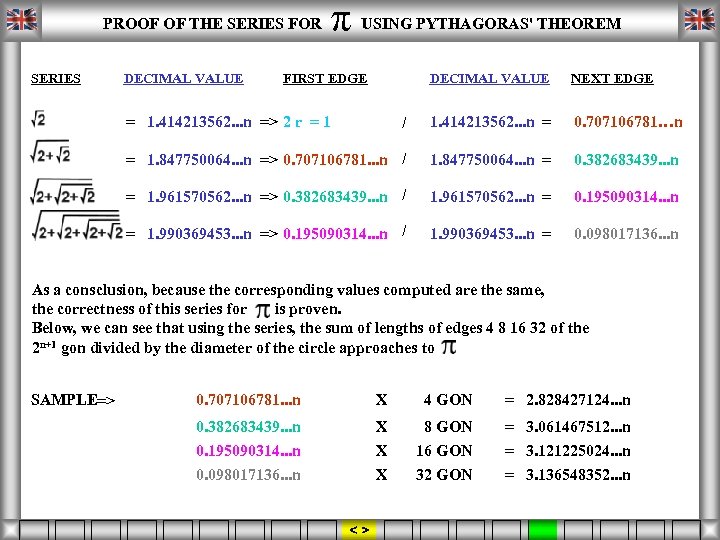
ORDER π FIRST EDGE NEXT EDGE FOUND RATIO PROOF OF THE SERIES FOR USING PYTHAGORAS' THEOREM SERIES DECIMAL VALUE NEXT EDGE / 1. 414213562. . . n = 0. 707106781…n = 1. 847750064. . . n => 0. 707106781. . . n / 1. 847750064. . . n = 0. 382683439. . . n = 1. 961570562. . . n => 0. 382683439. . . n / 1. 961570562. . . n = 0. 195090314. . . n = 1. 990369453. . . n => 0. 195090314. . . n / DECIMAL VALUE FIRST EDGE 1. 990369453. . . n = 0. 098017136. . . n = 1. 414213562. . . n => 2 r = 1 As a consclusion, because the corresponding values computed are the same, the correctness of this series for is proven. Below, we can see that using the series, the sum of lengths of edges 4 8 16 32 of the 2 n+1 gon divided by the diameter of the circle approaches to SAMPLE=> 0. 707106781. . . n X 4 GON = 2. 828427124. . . n 0. 382683439. . . n X 8 GON = 3. 061467512. . . n 0. 195090314. . . n 0. 098017136. . . n X X 16 GON 32 GON = 3. 121225024. . . n = 3. 136548352. . . n < >

ORDER FIRST EDGE NEXT EDGE THE HİSTORY OF. π FOUND RATIO 1. is an irrational and transcendental number ( a decimal with an infinite number of decimal places ), for example Japan’s Yasuma KANADA has carried to 206 158 430 000 decimal places as a world record. To prove and understand you have to know about trigonometry, logarithm, integral, limit, etc. Unfortunately seventh grade students cannot comprehend these calculations. 2. However, the formulas and series suggested above are easily understood by 7 th grade students who only know and four mathematical operation. There is not c 2=a 2 + b 2 any other calculation as simple as those that we have suggested. 3. Archimedes found the third decimal place of , Ulug Bey’s astronomer Al-Kasi carried it to 16 decimal places in 1479, in 1579 F. Viete figured out 9 decimals of and wrote an infinite series equals 2 / , Adrian Van Roomen found 15 decimal place of in 1593, and Ludolph Van Coulen had spent most of his life when finally in 1610 he carried to 35 decimal places. < >
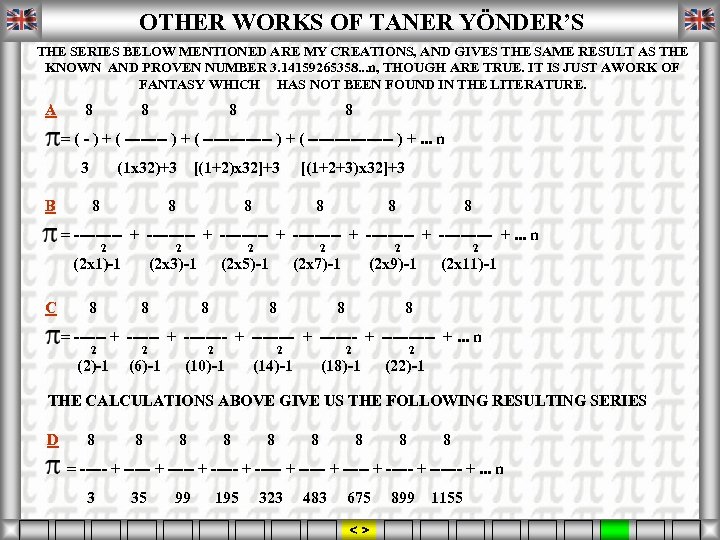
ORDER FIRST EDGE NEXT EDGE FOUND RATIO OTHER WORKS OF TANER YÖNDER’S THE SERIES BELOW MENTIONED ARE MY CREATIONS, AND GIVES THE SAME RESULT AS THE KNOWN AND PROVEN NUMBER 3. 14159265358. . . n, THOUGH ARE TRUE. IT IS JUST AWORK OF FANTASY WHICH HAS NOT BEEN FOUND IN THE LITERATURE. A 8 8 8 = ( - ) + ( ------------- ) + ( -------- ) +. . . n 3 (1 x 32)+3 [(1+2)x 32]+3 [(1+2+3)x 32]+3 B 8 8 = --------- + ----- +. . . n 2 2 (2 x 1)-1 (2 x 3)-1 (2 x 5)-1 (2 x 7)-1 (2 x 9)-1 (2 x 11)-1 C 8 8 8 = ------ + -------- + ----- +. . . n 2 2 (2)-1 (6)-1 (10)-1 (14)-1 (18)-1 (22)-1 THE CALCULATIONS ABOVE GIVE US THE FOLLOWING RESULTING SERIES D 8 8 8 = ----- + ----- + ------ +. . . n 3 35 99 195 323 483 675 899 1155 < >
ORDER FIRST EDGE NEXT EDGE ABAUT THE AUTHOR FOUND RATIO I was born in 1947, in Manisa, Turkey. I couldn’t go to school after the 8 th grade. I am a tire dealer now. Since I am interested in numbers I became an amateur mathematician. When I sawx x 10 : 9 and its square I was fascinated by the nature of the numbers. I had thought x 10 : 9 = 3. 14269680529. . n could be it self but after I few years when I learnt advanced math and irrational and transcendental numbers I understood why this can’t be However I believed that could be proven by some other easier ways without trigonometry. I realized something that had been ignored or missed for 2000 years: the ratio between the polygons’ edge-lengths. As shown before, the calculations are all correct. While there is such an easy way to understand prove , why do mathematicians still try to prove or calculate through difficult methods? I would like to teach to children and young mathematicians by my theory in school books. Taner Yönder KENAN EVREN SANAYİ SİTESİ 1299 ADA NO: 39 MANİSA / TURKEY TEL & FAX : 00 90 236 233 33 33 < >

ORDER FIRST EDGE NEXT EDGE APPROVAL FOUND RATIO These results were evaluated by our department of mathematics and approved to declare in our web site of university. Prof. Dr. Necdet BİLDİK Mathematical department Celal Bayar University. Phone : 00 90 ( 236 ) 201 32 03 Manisa - TURKEY e-mail : necdet. bildik@bayar. edu. tr < >
caed2f1c2833bfd9a8ab5c51ec024866.ppt