IC T Reaction Rate Theory k A

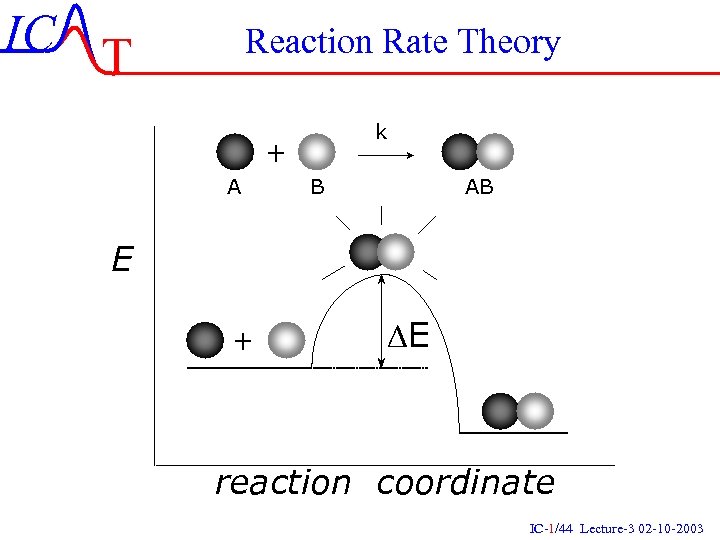IC T Reaction Rate Theory k + A B AB E + DE reaction coordinate IC-1/44 Lecture-3 02 -10 -2003

IC T The Arrhenius Equation k + A r = B AB d [AB] = k [A] [B] dt k = ve - Eact / RT E + Eact Svante Arrhenius 1859 - 1927 Nobel Prize 1903 reaction parameter Empirical ! IC-2/44 Lecture-3 02 -10 -2003

IC T Transition State Theory To determine the rate we must know the concentration on top of the barrier. The relative concentration between a reactant and product in a Chemical reaction is given by the Chemical Equilibrium The Chemical Equilibrium is given by the chemical potential of the reactant and the product. That we know how to calculate. IC-3/44 Lecture-3 02 -10 -2003

IC T The Chemical Equilibrium The chemical potential for the reactant and the product can be determined if we know their Partition Functions Q. Here Qi is the partition function for the gas i and qi the partition function for the gas molecule i Let us assume that we know qi then IC-4/44 Lecture-3 02 -10 -2003

IC T The Chemical Equilibrium If we assume an ideal gas and normalize the pressure with p 0=1 bar We obtain the important result that the Equilibrium Constant K(T) is given by the Partitions Functions of the reactants and products Thus we can determine the concentration of a product on top of the barrier if we know the relevant Partion Functions IC-5/44 Lecture-3 02 -10 -2003

IC T Partition Functions Obviously are Partition Functions relevant. We shall here deal with the Canonical Partition Function in which N, V, and T are fixed. Remember, that although we talk of a partition function for an individual molecule we always should keep in mind that this only applicable for a large ensample of molecules, i. e. statistics Consider a system with i energy levels with energy ei and degeneration gi Where Pi is the probability for finding the system in state i IC-6/44 Lecture-3 02 -10 -2003

IC T Ludwig Boltzmann (1844 -1906) Pi = Boltzmann Statistics: e - e i / RT ¥ å e - e i / RT i=0 The high temperature/diluted limit of S = k ln (W) Real statistical thermodynamics There is some really interesting Physics here!! IC-7/44 Lecture-3 02 -10 -2003

IC T Partition Functions Why does the partition function look like this? Lets see if we can rationalize the expression: Let us consider a system of N particles, which can be distributed on i states with each the energy ei and Ni particles. It is assumed the system is very dilute. I. e. many more available states than particles. Constraint 1 Constraint 2 Requirement: The Entropy should be maximized (Ludwig Boltzmann) IC-8/44 Lecture-3 02 -10 -2003

IC T Partition Functions Where we have utilized Stirling approximation: Only valid for huge N Problem: Optimize the entropy and fulfill the two constraints at the same time. USE LAGRANGE UNDERTERMINED MULTIPLIERS 0 0 IC-9/44 Lecture-3 02 -10 -2003

IC T Partition Functions Result: The Entropy Maximized when If we now utilize the first constraints: Which reminds us of q the partition function IC-10/44 Lecture-3 02 -10 -2003

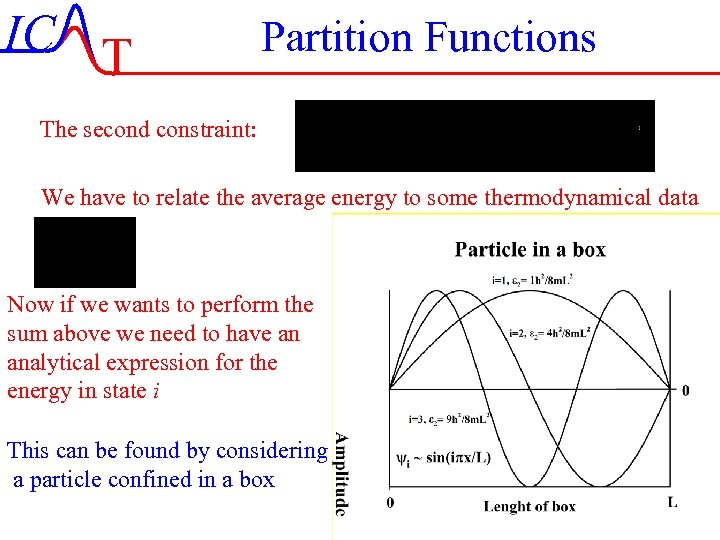IC T Partition Functions The second constraint: We have to relate the average energy to some thermodynamical data Now if we wants to perform the sum above we need to have an analytical expression for the energy in state i This can be found by considering a particle confined in a box IC-11/44 Lecture-3 02 -10 -2003

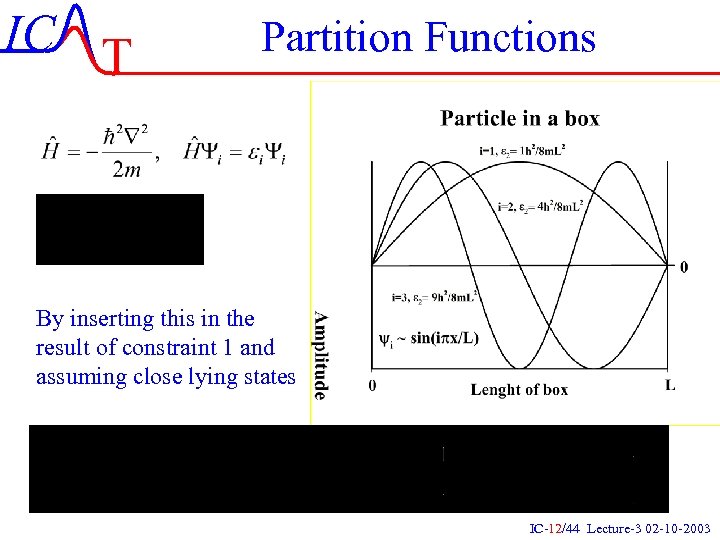IC T Partition Functions By inserting this in the result of constraint 1 and assuming close lying states IC-12/44 Lecture-3 02 -10 -2003

IC T Partition Functions Utilizing this in constraint 2 Thus I. e. temperature is just a Lagrange multiplyer IC-13/44 Lecture-3 02 -10 -2003

IC T Partition Functions Since constraint 1 gave Since constraint 2 gave and the entropy is max for Thus the form of the partition function comes as a result of maximizing the entropy with 2 constraints IC-14/44 Lecture-3 02 -10 -2003

IC T Translational Partition Functions As we have assumed the system to be a particle capable of moving in one dimension we have determined the one-dimensional partition function for translational motion in a box of length l Now what happens when we have several degrees of freedom? If the different degrees of freedom are independent the Hamiltonian can be written as a sum of Hamiltonians for each degree of freedom Htot=H 1+H 2+…. Discuss the validity of this: When does this not work? Give examples IC-15/44 Lecture-3 02 -10 -2003

IC T Translational Partition Functions If the hamiltonian can be written as a sum the different coordinates are indrependant and Thus for translational motion in 3. Dimensions. qtrans 3 D = qtransx qtransy qtransz= IC-16/44 Lecture-3 02 -10 -2003

IC T Partition Functions It is now possible to understand we the Maxwell-Boltzman distribution comes from IC-17/44 Lecture-3 02 -10 -2003

IC T Maxwell-Boltzmann distribution of velocities Average: 500 – 1500 m/s at 300 K IC-18/44 Lecture-3 02 -10 -2003

IC T Partition Functions Similarly can we separate the internal motions of a molecule in Part involving vibrations, rotation and nuclei motion, and electronic motion i. e. for a molecule we have Now we create a system of many molecules N that are in principle independent and as they are indistinguishable we get an overall partition function Q What if they were distinguishable ? ? ? IC-19/44 Lecture-3 02 -10 -2003

IC T Partition Functions What was the advantage of having the Partition Function? IC-20/44 Lecture-3 02 -10 -2003

IC T Partition Functions Similarly can we separate the internal motions of a molecule in Part involving vibrations, rotation and nuclei motion, and electronic motion i. e. for a mulecule we have Now we create a system of many molecules N that are in principle independent and as they are indistinguishable we get an overall partition function Q IC-21/44 Lecture-3 02 -10 -2003

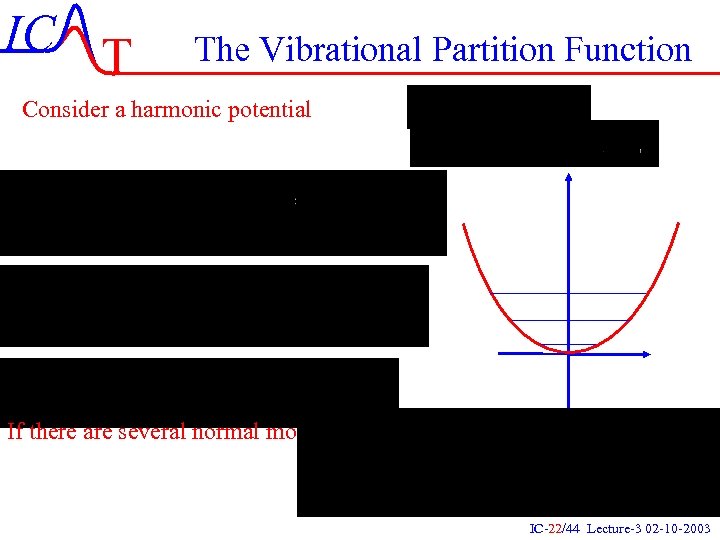IC T The Vibrational Partition Function Consider a harmonic potential If there are several normal modes: IC-22/44 Lecture-3 02 -10 -2003

IC T The Rotational (Nuclear) Partition Function Notice: Is not valid for H 2 WHY? TRH 2=85 K, TRCO=3 K IC-23/44 Lecture-3 02 -10 -2003

IC T The Rotational (Nuclear) Partition Function Types of molecules C 1, Ci, and Cs 1 CO, CHFCl. Br, mesotartraric acid, and CH 3 OH C 2, C 2 v, and C 2 h 2 H 2, H 2 O, and transdichloroethylene C 3 v and C 3 h The Symmetri factor: This has strong impact on the rotational energy levels. Results in fx Ortho- and para-hydrogen Molecular symmetry 3 NH 3, and planar B(OH)3 For a non-linear molecule: IC-24/44 Lecture-3 02 -10 -2003

IC T Effect of bosons and fermions If two fermions (half intergral spin) are interchanges the total wave function must be anti symmetric i. e. change sign. Consider Hydrogen each nuclei spin is I=1/2 From two spin particles we can form 2 nuclear wave function: and which are (I+1)(2 I+1)=3 and I(I+1)=1 degenerate respectively Since the rotation wave function has the symmetry is it easily seen that if the nuclear function is even must j be odd and visa versa IC-25/44 Lecture-3 02 -10 -2003

IC T Ortho and Para Hydrogen This means that our hydrogen comes in two forms: Ortho Hydrogen Which has odd J and Para Hydrogen which has even J incl. 0 Notice there is 3 times as much Ortho than Para, but Para has the lowest energy a low temperature. If liquid Hydrogen should ever be a fuel we shall see advertisements Hydroprod Inc. Absolute Ortho free Hydrogen for longer mileages IC-26/44 Lecture-3 02 -10 -2003

IC T Liquid Hydrogen This has severe consequences for manufacturing Liq H 2 !! The ortho-para exchange is slow but will eventually happen so if we have made liq. hydrogen without this exchange being in equilibrium we have build a heating source into our liq. H 2 as ¾ of the H 2 will End in J=1 instead of 0. i. e. 11% loss due to the internal conversion of Ortho into Para hydrogen IC-27/44 Lecture-3 02 -10 -2003

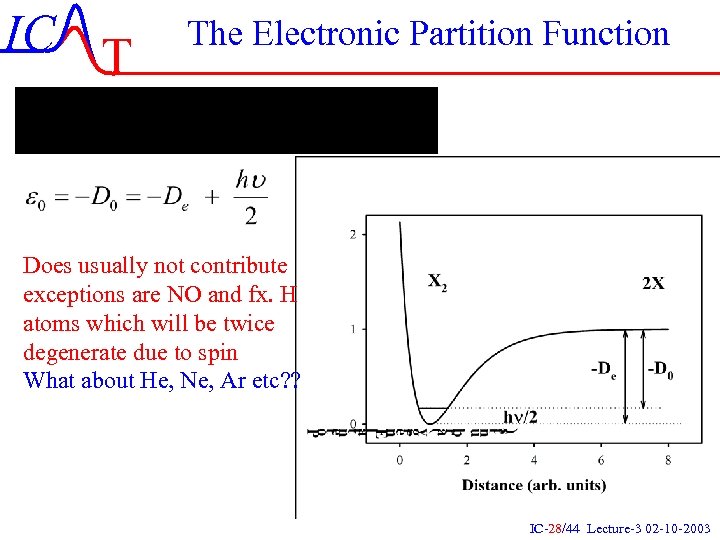IC T The Electronic Partition Function Does usually not contribute exceptions are NO and fx. H atoms which will be twice degenerate due to spin What about He, Ne, Ar etc? ? IC-28/44 Lecture-3 02 -10 -2003

IC T Partition Functions Summary IC-29/44 Lecture-3 02 -10 -2003

IC T Partition Functions Example Knowing the degrees of internal coordinates and their energy distribution calculate the amount of molecules dissociated into atoms a different temperatures. T(K) p. H/p 0 KN 2(T) p. N/p 0 KO 2(T) p. O/p 0 298 5. 81*10 -72 2. 41*10 -36 6. 35*10 - 2. 52*10 -80 6. 13*10 -81 7. 83*10 -41 1000 5. 24*10 -18 3. 13*10 -6 2. 29 *10 -9 1. 76*10 -3 2. 55*10 -43 5. 05*10 -22 4. 12*10 -19 6. 42*10 -10 2000 2. 23*10 -18 1. 80*10 -9 1. 22*10 -5 3. 49*10 -3 3000 KH 2(T) 1. 77*10 -3 1. 72*10 -1 1. 01*10 -9 3. 18*10 -5 5. 04*10 -1 5. 01*10 -1 160 We see why we cannot make ammonia in the gas phase but O radicals may make NO at elevated temperatures IC-30/44 Lecture-3 02 -10 -2003

IC T Surface Collisions Consider a box with volume V What are the numbers? IC-31/44 Lecture-3 02 -10 -2003

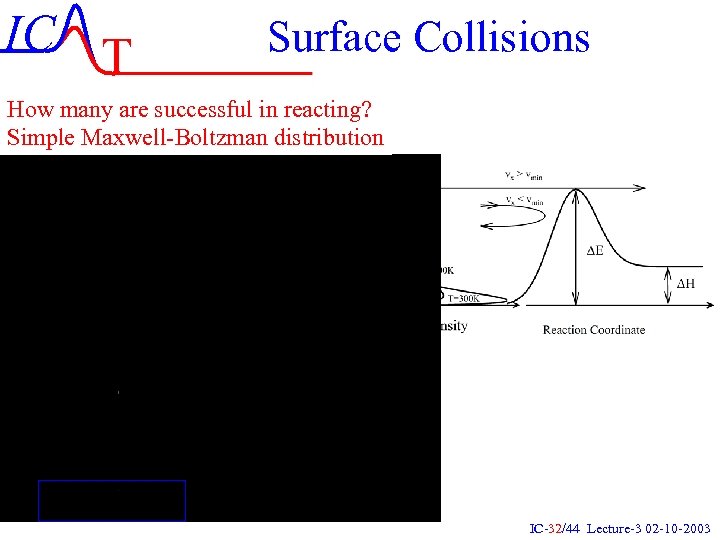IC T Surface Collisions How many are successful in reacting? Simple Maxwell-Boltzman distribution IC-32/44 Lecture-3 02 -10 -2003

IC T Transition State Theory R# Consider the following reaction: q`# P How? n is a frequency or trial factor in the reaction coordinate R We assume that R and R# are in Equilibrium IC-33/44 Lecture-3 02 -10 -2003

IC T Transition State Theory By splitting the partition function in the transition state Assuming IC-34/44 Lecture-3 02 -10 -2003

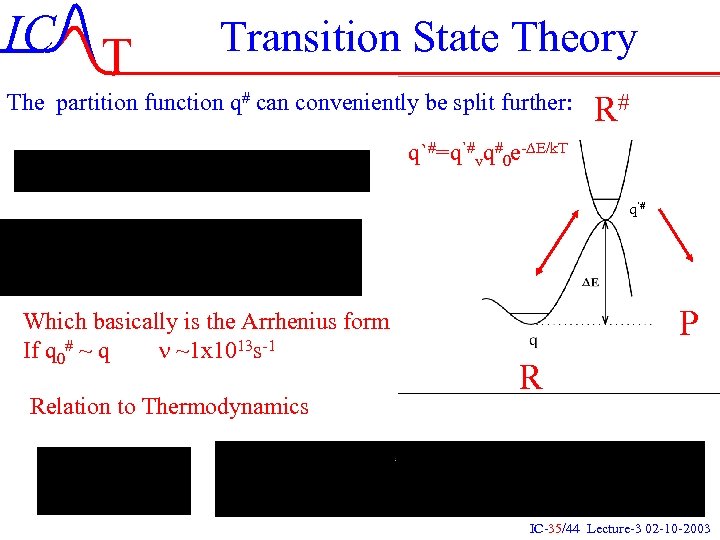IC T Transition State Theory The partition function q# can conveniently be split further: R# q`#=q`#vq#0 e-DE/k. T q`# Which basically is the Arrhenius form If q 0# ~ q n ~1 x 1013 s-1 Relation to Thermodynamics P R IC-35/44 Lecture-3 02 -10 -2003

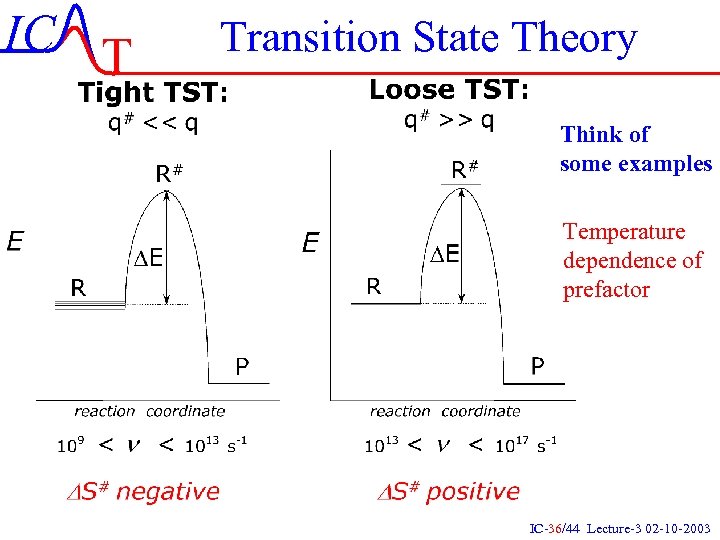IC T Transition State Theory Think of some examples Temperature dependence of prefactor IC-36/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Indirect adsorption of atoms: An atom adsorbs into a 2 -dim mobile state, we have Ng gas atoms, M sites on the surface, and N# atoms in the transition state IC-37/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Now what is K# ? IC-38/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces This corresponds to the collision on a surface since the atoms are still free to move in two dimensions IC-39/44 Lecture-3 02 -10 -2003

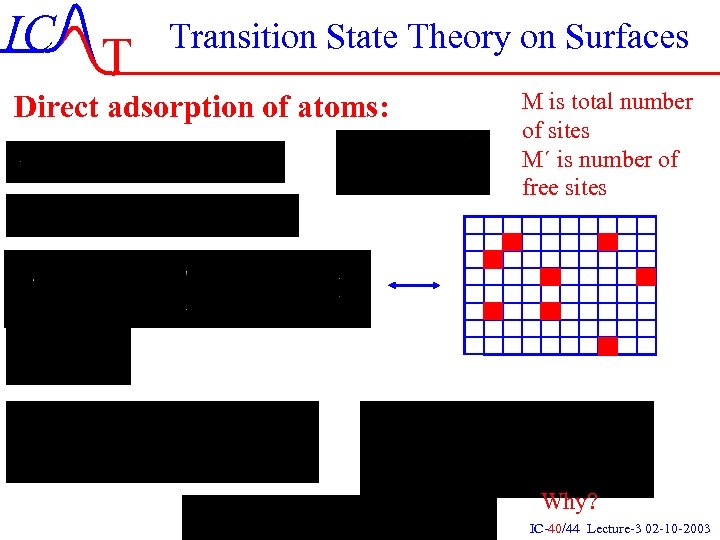IC T Transition State Theory on Surfaces Direct adsorption of atoms: M is total number of sites M´ is number of free sites Why? IC-40/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces IC-41/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Notice adsorption always result in loss of entropy There may also be steric hindrance leading to reduced S IC-42/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces What happens in the regime between direct and indirect adsorption? The atoms breaks free of the site and start to diffuse around in Eventually IC-43/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Indirect adsorption of molecules: Notice that if the precursor is sufficiently loose S 0(T)=1. IC-44/44 Lecture-3 02 -10 -2003

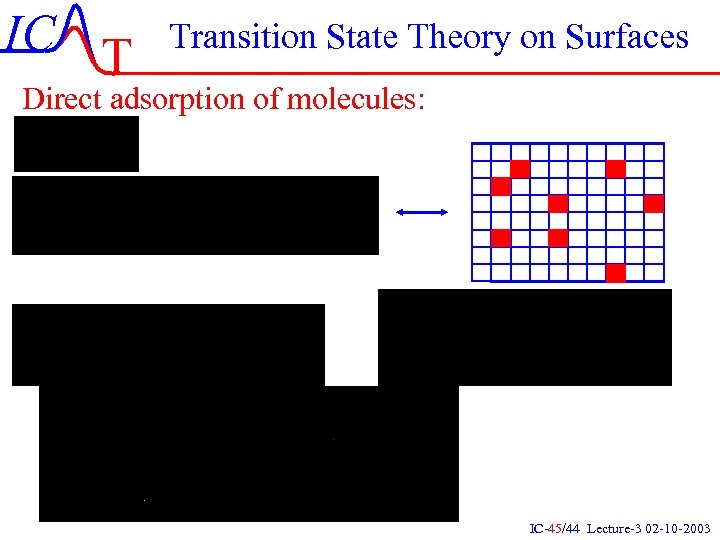IC T Transition State Theory on Surfaces Direct adsorption of molecules: IC-45/44 Lecture-3 02 -10 -2003

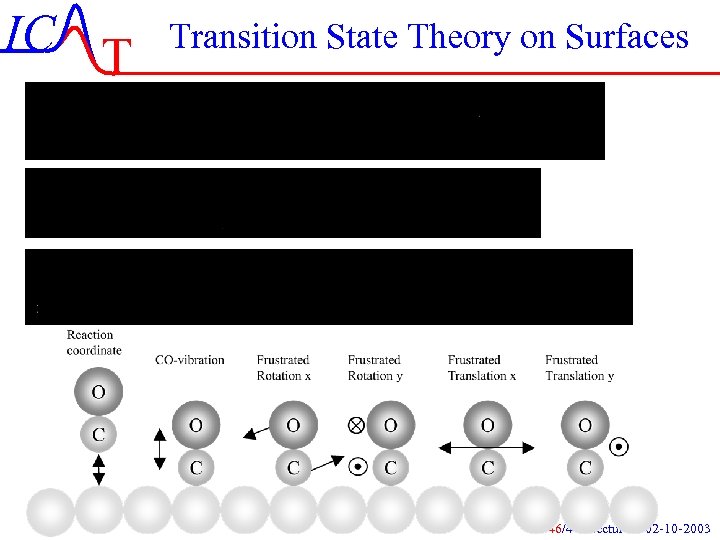IC T Transition State Theory on Surfaces IC-46/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Reactions between surface species: IC-47/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces The reverse process: IC-48/44 Lecture-3 02 -10 -2003

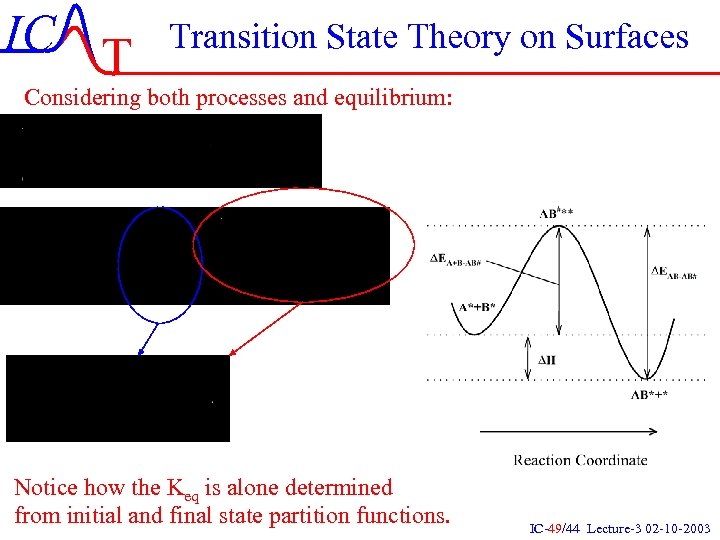IC T Transition State Theory on Surfaces Considering both processes and equilibrium: Notice how the Keq is alone determined from initial and final state partition functions. IC-49/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces Desorption: IC-50/44 Lecture-3 02 -10 -2003

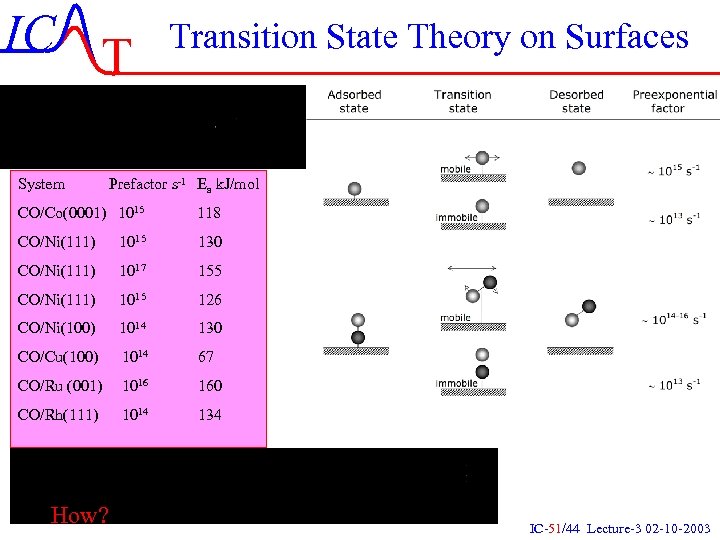IC T Transition State Theory on Surfaces System Prefactor s-1 Ea k. J/mol CO/Co(0001) 1015 118 CO/Ni(111) 1015 130 CO/Ni(111) 1017 155 CO/Ni(111) 1015 126 CO/Ni(100) 1014 130 CO/Cu(100) 1014 67 CO/Ru (001) 1016 160 CO/Rh(111) 1014 134 How? IC-51/44 Lecture-3 02 -10 -2003

IC T Transition State Theory on Surfaces If the details of the transition state can be determined can the rate over the barrier be calculated. Details of the transition state are difficult to access: • Low concentration • Short lifetime. Often determined by ``First Principle´´ calculations, but are only accurate to say 0. 1 e. V or 10 k. J/mol. IC-52/44 Lecture-3 02 -10 -2003