IBM Research Zurich Anonymous Credentials on a Standard

IBM Research, Zurich Anonymous Credentials on a Standard Java Card joint work with supported by Thomas Gross Patrik Bichsel, Jan Camenisch, Victor Shoup IBM’s Blue. Z Group for Strong Authentication 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Overview § Introduction § Camenisch-Lysyanskaya Signatures § Problem Statement § Key Ideas § Results 2 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

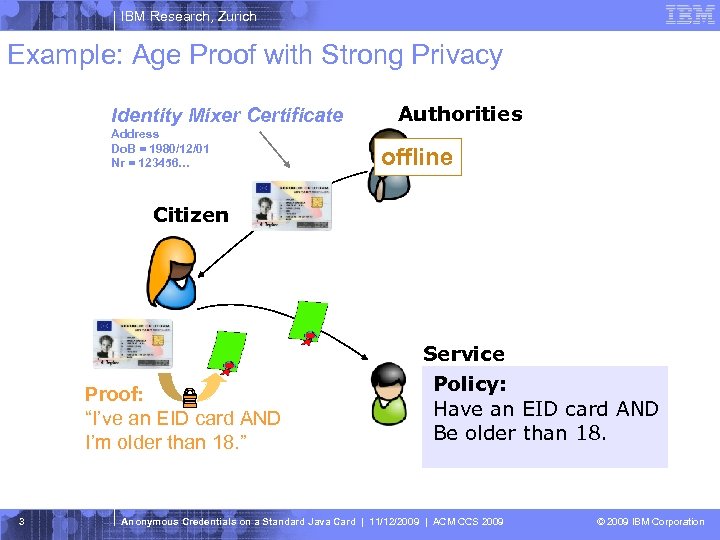
IBM Research, Zurich Example: Age Proof with Strong Privacy Identity Mixer Certificate Address Do. B = 1980/12/01 Nr = 123456… Authorities offline Citizen Proof: “I’ve an EID card AND I’m older than 18. ” 3 Service Policy: Have an EID card AND Be older than 18. Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Java Card* Limitations § 8 -bit CPU (3. 57 MHz) § Limited access to public key-CP (only standard RSA, DSA) § Limited RAM (2 K) *: JCOP 41/v 2. 2 4 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Basis: Camenisch-Lysyanskaya Signatures [Camenisch & Lysyanskaya ’ 01] Public key of signer: RSA modulus n and ai, b, d Є QRn, Secret key: factors of n Signature of L attributes m 1, . . . , m. L Є {0, 1}ℓ : (c, e, s) For random prime e > 2ℓ and integer s ≈ n, compute c such that d = a m 1·. . . · a 1 m. L L bs ce mod n Theorem: Signature scheme is secure against adaptively chosen message attacks under SRSA assumption. [SRSA: Barić & Pfitzmann '97 and Fujisaki & Okamoto '97] Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Basis: Camenisch-Lysyanskaya Signatures [Camenisch & Lysyanskaya ’ 01] Signature of L attributes m 1, . . . , m. L Є {0, 1}ℓ : (c, e, s) For random prime e > 2ℓ and integer s ≈ n, compute c such that d = a m 1·. . . · a 1 m. L L bs ce mod n Abstractly requires computation of: x 1 xi A ·. . . · A 1 i x. L L mod n where xi correspond to attributes in the certificates and potentially |xi| > |n| Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

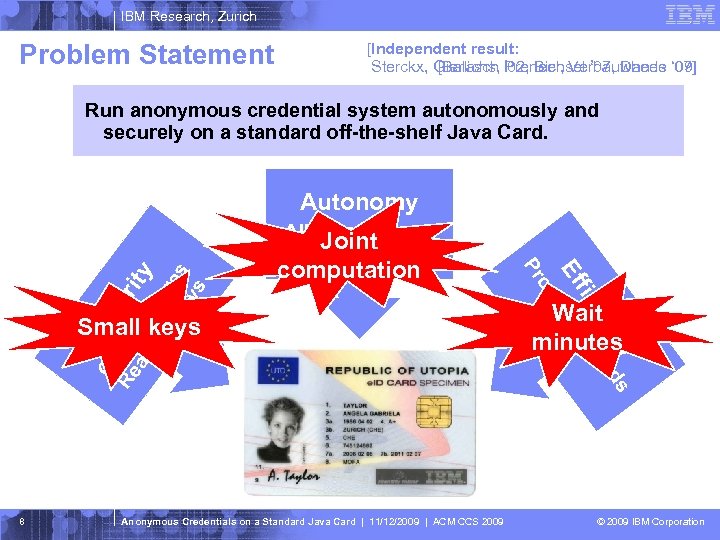
IBM Research, Zurich Problem Statement [Independent result: Sterckx, Gierlichs, ’ 02, Bichsel ’ 07, Danes ‘ 07] [Balasch Preneel, Verbauwhede ‘ 09] Run anonymous credential system autonomously and securely on a standard off-the-shelf Java Card. Autonomy CL Sec Re -Si ur al gn ity is at tic ur ke es ys 8 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 y nc ds ie on fi c s e c E f f in Small keys oo computation Pr All data on card Joint Malicious terminal Wait minutes © 2009 IBM Corporation

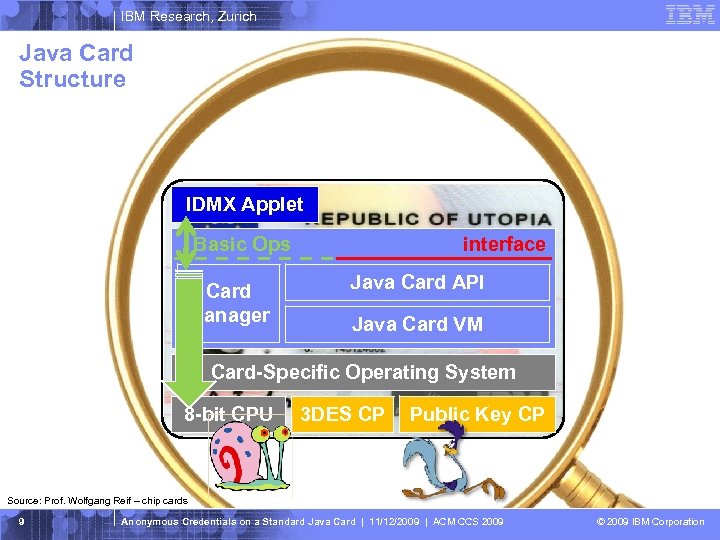
IBM Research, Zurich Java Card Structure IDMX Applet Basic Ops Card Manager interface Java Card API Java Card VM Card-Specific Operating System 8 -bit CPU 3 DES CP Public Key CP Source: Prof. Wolfgang Reif – chip cards 9 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

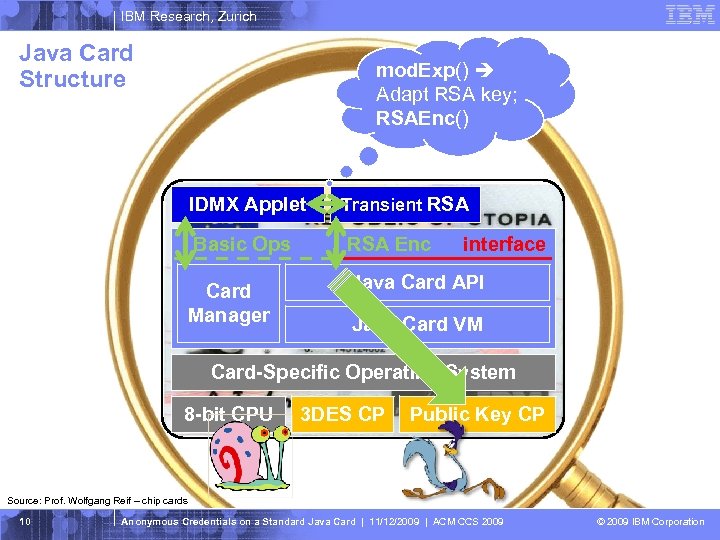
IBM Research, Zurich Java Card Structure mod. Exp() Adapt RSA key; RSAEnc() IDMX Applet Transient RSA Basic Ops RSA Enc interface Card Manager Java Card API Java Card VM Card-Specific Operating System 8 -bit CPU 3 DES CP Public Key CP Source: Prof. Wolfgang Reif – chip cards 10 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich (Ab-)Using Standard RSA Interface § Recall RSA Encryption: me mod n (Limited size of e) § Mod. Exp() with Big Exponents Split exponents: A 1 x 1 A 2 x 2 = A 1 x 11 + x 12*2 k A 2 x 21 + x 22*2 k mod n = A 1 x 11 A’ 1 x 12 A 2 x 21 A’ 2 x 22 mod n = A 1 x 11(A 12 k) x 12 A 2 x 21(A 22 k)x 22 mod n § Mod. Multiply(): RSA interface can only do exponentiation Reduce multiply to mod. Exp() by binomial formula: A*B 11 = ((A+B)2 - A 2 - B 2)/2 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 mod n © 2009 IBM Corporation

IBM Research, Zurich Results § Anonymous credential system on standard Java Card • JCOP 41/v 2. 2 • Future: Java Card 3. 0 standard § Attributes: Focus on proof of possession • rely on hardware tamper resistance for statement, and • detect / revoke broken cards. § Autonomous: secure in face of untrusted terminal § Efficient: 10 sec (at 1536 bits) 7. 5 sec pre-computation / 2. 5 sec on-line 13 Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich BACKUP 14 Anonymous Credentials on a Standard Java Card | 11/12/2009

IBM Research, Zurich Detailed Performance Analysis: Modulus 1536 bit Amortized Estimates over 1000 Ops, Upper Bound on Parameter Length, Percent Rounded Down Function Time Ops Percent Multiplication 4’ 653 ms 9 Ops 39 % 2988 ms 36 Ops 25 % 243 ms 27 Ops 2% Mod. Exp 4’ 308 ms 10 Ops 36 % SRNG 1’ 088 ms 16 Ops 9% TRNG 815 ms 1 Op 6% Addition 581 ms 7 Ops 4% Digest 220 ms 10 Ops 1% Addition Mod. Square Total 15 11’ 665 ms Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Recall: The Strong RSA Assumption Flexible RSA Problem: Given RSA modulus n and z Є QRn find integers e and u such that ue = z mod n (Recall: QRn = {x : exist y s. t. y 2 = x mod n } ) ● Introduced by Barić & Pfitzmann '97 and Fujisaki & Okamoto '97 ● Hard in generic algorithm model [Damgård & Koprowski '01] Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Signature Scheme based on the SRSA I [Camenisch & Lysyanskaya ‘ 02] Public key of signer: RSA modulus n and ai, b, d Є QRn, Secret key: factors of n To sign k messages m 1, . . . , mk Є {0, 1}ℓ : ● choose random prime e > 2ℓ and integer s ≈ n ● compute c such that d = a m 1·. . . · a 1 ● mk k bs ce mod n signature is (c, e, s) Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Signature Scheme based on the SRSA II A signature (c, e, s) on messages m 1, . . . , mk is valid iff: ● m 1, . . . , mk Є {0, 1}ℓ: ● e > 2ℓ ● d = a m 1·. . . · a 1 mk k bs ce mod n Theorem: Signature scheme is secure against adaptively chosen message attacks under SRSA assumption. Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Proof of Knowledge of a Signature Observe: Let c' = c bs'mod n with random s' then d = c‘ e a m 1 1 ·. . . · a mk k bs* (mod n), with s* = s-es’ i. e. , (c', e, s*) is a also a valid signature! Therefore, to prove knowledge of signature on some m ● provide c' ● PK{(e, m 1, . . . , mk, s) : d : = c'e a m 1 ·. . . · a 1 mk k bs Ù mi Є {0, 1}ℓ Ù e Є 2ℓ+1 ± {0, 1}ℓ } Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 © 2009 IBM Corporation

IBM Research, Zurich Proof of Knowledge of a Signature Using second Commitment assume second group 2 nd commitment n, ai, b, n C = a 1 sk b s* To prove knowledge of signature on some m provide c' PK{(e, m 1, . . . , mk, s, s* ) : C = a 1 m 1 b s* Ù d : = c‘ e a m 1 1 ·. . . · a Anonymous Credentials on a Standard Java Card | 11/12/2009 | ACM CCS 2009 mk k bs } © 2009 IBM Corporation